Параметрическая оптимизация рабочих процессов магнитореологических приводных систем

В распространенных магнитореологических системах реализовано управление, основанное на изменении вязкости рабочей среды во внешних электромагнитных полях, что накладывает на магнитореологические приводы существенные ограничения по диапазону параметров регулирования. Прежде всего, это связано с неспособностью увеличения вязкости магнитореологической среды во внешних электромагнитных полях более чем на 30–50 % и сложностью стабилизации ее температуры. Очевидно, что нестабильность реологических характеристик и лимитированность роста вязкостных параметров негативно отражаются на динамике и глубине регулирования магнитореологических приводов. Наиболее распространенные конструкции регулирующих устройств, применяемых в магнитореологических приводных системах, и способы организации управления в них приведены в работах [1–12].

Актуальность. Приводы являются неотъемлемой частью автоматизированных систем и во многом определяют их эффективность, надежность и точность отработки сигнала управления, поэтому оптимизация рабочих характеристик магнитореологических приводных систем актуальна и востребована.

Задача исследовательской работы: разработать способ улучшения динамики и увеличения глубины регулирования магнитореологических приводных систем. Для предлагаемого способа произвести параметрическую оптимизацию процесса регулирования расходных характеристик.

Способ регулирования характеристик магнитореологических приводных систем

В рамках данной исследовательской работы рассмотрим комбинированный способ реализации регулирования в магнитореологических приводных системах как за счет изменения вязкости и генерирования гидродинамических и реологических эффектов во вращающихся и винтовых управляющих электромагнитных полях, так и путем сочетания объемного и дроссельного методов. Как известно, объемный метод управления расходом энергетически более эффективен в сравнении с дроссельным методом. Реализация объемного метода при помощи классической гидравлической аппаратуры не всегда экономически целесообразна, что связано с высокими затратами на производство источников давления, а конструкции магнитодинамических насосов и магнитореологических дросселей принципиально схожи и не имеют существенной разницы в стоимости. Комбинированный способ регулирования в магнитореологических приводных системах организован следующим образом. С целью улучшения динамических параметров регулирования привода, для создания перепада давления и запирания потока магнитореологической жидкости применяется сочетание эффектов изменения вязкости и динамического запирания потока, которые возникают при организации вращающегося движения рабочей жидкости в кольцевом канале, что реализовано посредством управляющего электромагнитного поля. Вращающееся управляющее электромагнитное поле создается группой элементов блока электромагнитного управления потоком, расположенных по периферии кольцевого канала проточной части; при последовательном включении элементов блока электромагнитного управления потоком магнитореологическая жидкость движется вращательно-поступательно, образуя эффект динамического вихревого запирания потока. Регулирование гидравлического сопротивления в рабочей зоне магнитореологического устройства осуществляется в зависимости от скорости изменения характеристик электромагнитного поля и частоты переключения элементов кольцевой дифференциальной обмотки блока электромагнитного управления. Магнитодинамический насос (рис. 1) обеспечивает повышение эффективности и снижение потерь электрической мощности привода, так как применяется управление не только посредством магнитореологических дросселей, но дополнительно используется регулируемый магнитодинамический насос.

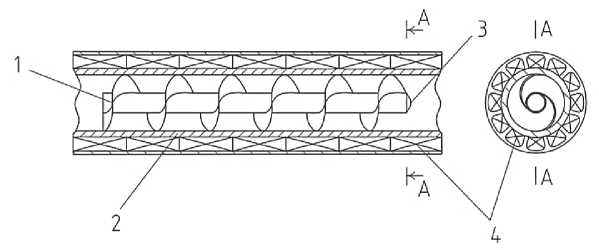
Рис. 1. Магнитодинамический насос: 1 – шнек, 2 – корпус, 3 – обтекатель, 4 – каскад блоков электромагнитного управления потоком

Изменение параметров, частоты смены сигналов на элементах блоков управления магнитодинамического насоса и длительности электрических импульсов приводит к изменению гидравлических параметров потока магнитореологической жидкости, а изменение частоты смены сигналов и длительности электрических импульсов, подаваемых на блоки электромагнитного управления магнитореологических дросселей, позволяет осуществлять точное дорегулирование рабочих характеристик магнитореологического привода. Подача рабочей среды магнитодинамическим насосом осуществляется бегущим винтовым электромагнитным полем, индуцируемым каскадом блоков электромагнитного управления потоком, которые состоят из элементов дифференциальной обмотки и образуют рабочие зоны магнитодинамического насоса. По сигналу контроллера происходит включение обмоток каждого последующего блока, при этом включение обмотки блока начинается со смещения на один элемент дифференциальной обмотки, то есть с угловым сдвигом.

Развернутое описание предлагаемого способа приведено в опубликованных ранее работах [13-15].

Численное описание рабочего процесса при эксплуатации магнитореологических устройств, применяющих вращающиеся и винтовые управляющие электромагнитные поля

Так как в предлагаемых устройствах реализованы вращающиеся и винтовые управляющие электромагнитные поля, для описания гидродинамики рабочего процесса введем понятие спиральности потока [16]. Скорость изменения спиральности потока можно представить в виде:

dh „,      |             , v ² 1      .„|        „

— + v V h = го P + grad---gradP + vrotP d t              I 2 р I

dh

5t

- 9ro rot го - 9 vrot (rot го);

h = v го; го = rotv, где Pv - вектор плотности объемных сил, го - завихренность, v - скорость, h - спиральность, t -время, P - давление, 9 - кинематическая вязкость, р - плотность. В безразмерном виде:

v 2 a w

¹ 0 t 0 ^dT

3                                   32

+ v 0- U V W = -° ( V U - P ) + v 0- V UGradU— -v ⁰- V UGradP + 2 ^v 22

¹ 0              ¹ 0                  ¹ 0               ^{2 1} 0 ^р

+v0 (U -V Pv )-9v3 (V U )-(VV U )-9 v0- U (VVVU);

l 0                     l ₀ l ₀

W = -h-1₀ = U ( V U ) ; v = Uv ₀ ; r = Rl ₀ ; t = t 1 ₀ ; h = vrotv = v ⁰- U V U ; го = v ⁰ V U ,

v ₀

где 1 0 - показатель размера, 1 0 - показатель времени, v 0 - показатель скорости, U ; R ; т - безразмерные величины соответствующие физическим величинам, 1 ₀ ; 1 0 ; v 0 ; V ; Grad - дифференцирование по безразмерной координате. Или:

-l°- ^W + U V W = l°g (V U) + V UGradU1- V UGradP - v0t0 dT            v2                    2   v2P

Ta, sh^ + Ц r

.

_ 1      тM (H)41 + (tt sHM (H) / J)

Tx/i

— + Ц r

.

/ P

0 l 0

_ 1      тM (H)41 + (tt sHM (H) / J)

v ₀ l ₀

В критериальном виде:

i aw

--+ U V W = Wo St

We v

1 g

U L Fr\g\

U ²

+ Grad--Eu

GradP

w

—(V U ) - (W U )

/P

U (VVV U).

le (VVU) - lie Ue- (VVV U) •

Re

где e_v – единичный вектор в направлении тока. Критерий гомохромности:

W o = v 0 t 0 l ₀

.

Критерий Фруда:

Fr = ^2-.

l 0 g

Критерий Эйлера: Eu = -P- .

v o P

Критерий Рейнольдса:

Re = —------;----- v 0 l 0-----------

_ 1      т M ( H )

41 + ( тт _sHM ( H ) / J )

T.l, sh + Ц _r

.

/ р

.

Оценим влияние интенсивности завихренности k на скоростные характеристики потока: rotv = kv ; v to = kv ² ; h = kv ² .

В безразмерном виде:

W = KU 2 ; W = hl 0 ; K = kl ₀ ; U = U I = — ; v 0²                        v 0

kv v = v ; h = v to= v to cos a; a = nn; cos a =    .

to

Запишем уравнение сохранения энергии с учетом воздействия на поток электромагнитного поля [16–17]:

d

v

d T-^                '^v p— cvT + — =pPvv - div^pv i + —

dt

т

” + Ц r

.

к

т M (H)

+ 41 + ( тт s HM ( H ) / J )

I 2 i I grad\ v +— -к Pr)

т

— + Ц _r

.

1      т M ( H )

41 + ( тт _sHM ( H ) / J )

[ to v ] + -3 ц divv > + F ;

;

i = c p T = c v T + P / р ; Pr =

т

— + Ц _r

.

1     тM (H)

41 + ( тт _sHM ( H ) / J )

C p / X;

F = T, [ rotH ' ^H 1 -

4n где cv; cp – удельная теплоемкость среды при постоянных объеме и давлении, T – температура, X - теплопроводность, F - сила Лоренца [18]. Электродинамика рабочего процесса описывается системой уравнений Максвелла [18–20]:

^ = rot ( [ v - B ] - E ) ; rot—B = 4 n j ;

divB = 0; B = цH, где H – напряженность магнитного поля, B – магнитная индукция, E – напряженность электрического поля, j - плотность тока, ц - магнитная проницаемость. Выразим электромагнитные параметры через векторный потенциал A :

d A г

B = rotA; E =+ [ v - rotA ] ;

d t ^{[          ]}

rot—B = - rot—rotA; B = Bm sin (to mt + у m), ц ц где Bm - вектор амплитуды индукции магнитного поля, tom - частота магнитного поля, уm - фаза. Улучшение динамики, снижение времени переходных процессов и увеличение глубины регулирования магнитореологических приводных систем возможно за счет оптимизации базовых физических параметров управляющего электромагнитного поля. Так как управление расходными характеристиками происходит посредством электромагнитного поля, приравняем скорость бегущего магнитного поля к скоростным параметрам потока магнитореологической среды. Очевидно, что скорость в магнитодинамической модели зависит от вектора амплитуды индукции магнитного поля и частоты магнитного поля. Поэтому проведем параметрическую оптимизацию рабочего процесса по частотно-фазовому принципу.

Результаты численного эксперимента и обсуждение результатов

Зададим изменения магнитной индукции управляющего поля по синусоидальному закону (рис. 2, 3).

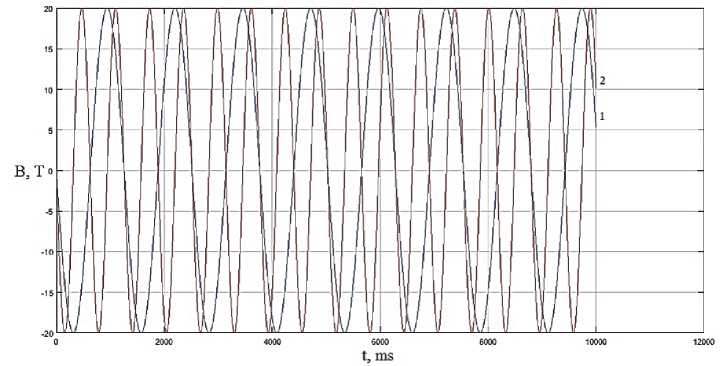
Рис. 2. Частотные характеристики индукции магнитного поля при значении частот 1 : и m = 5 Hz ; 2 : и m = 10 Hz и фазы, равной у m = п

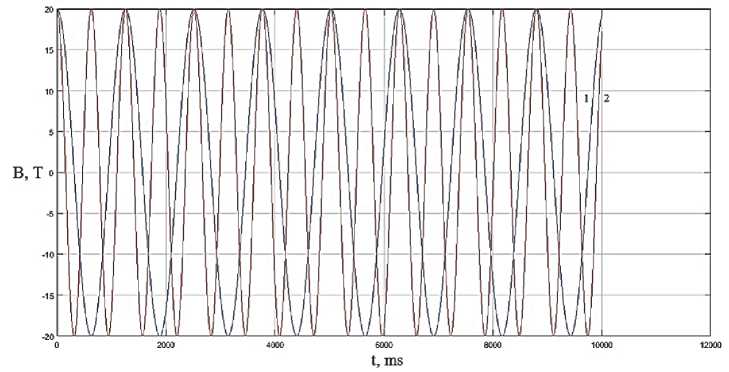
Рис. 3. Частотные характеристики индукции магнитного поля при значении частот 1 : и m = 5 Hz ; 2 : и m = 10 Hz и фазы, равной у m = п / 2

Создаваемое поле изменяется во времени, меняя направление вектора магнитной индукции на противоположное, принимая значения размагничивающего поля, позволяя производить размагничивание и последующее перемагничивание частиц магнетика. На основе заданных частотнофазовых параметров получим значения скорости изменения спиральности потока, позволяющие оценить динамику изменения гидродинамического вихря в потоке (рис. 4-7). Расчетные графики динамики скорости изменения спиральности потока иллюстрируют существенную зависимость рассматриваемого параметра от частотных и фазовых характеристик управляющего электромагнитного поля, так как являются функцией частоты и скорости. Результаты численного моделирования показывают, что скорость изменения спиральности потока является хорошей мерой динамики скоростных параметров вихревого движения потока магнитореологической жидкости.

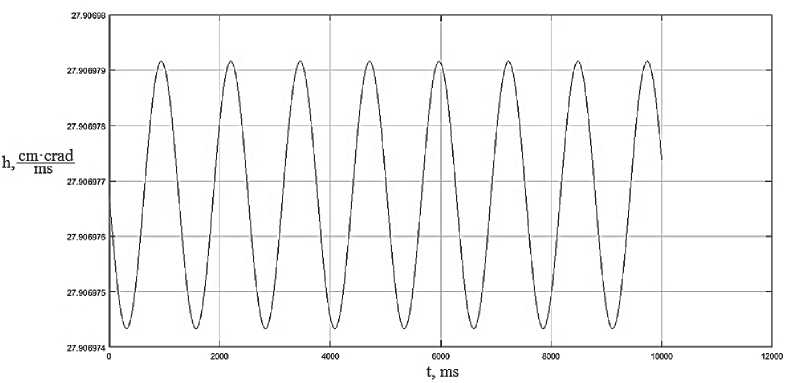
Рис. 4. Динамика скорости изменения спиральности потока при значении частоты гоm = 5Hz и фазы, равной уm = п

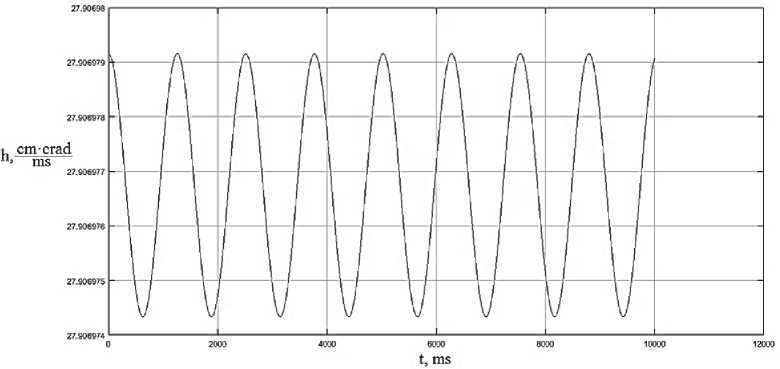
Рис. 5. Динамика скорости изменения спиральности потока при значении частоты го m = 5 Hz и фазы, равной у m = п / 2

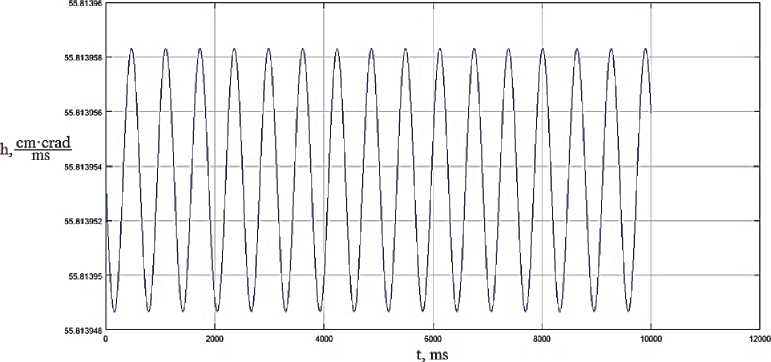
Рис. 6. Динамика скорости изменения спиральности потока при значении частоты гоm = 10Hz и фазы, равной уm =п

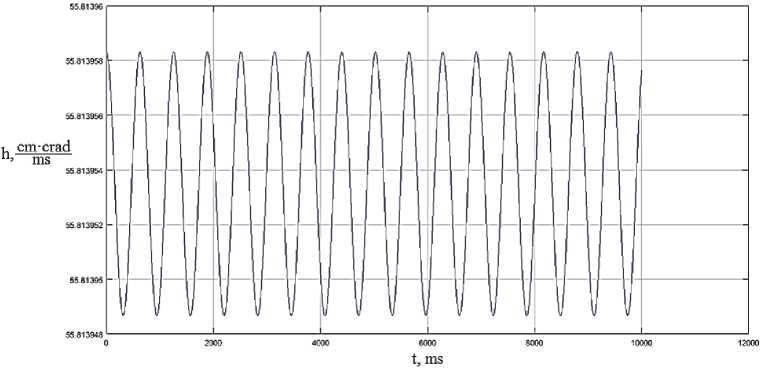
Рис. 7. Динамика скорости изменения спиральности потока при значении частоты го m = 10 Hz и фазы, равной у m = п / 2

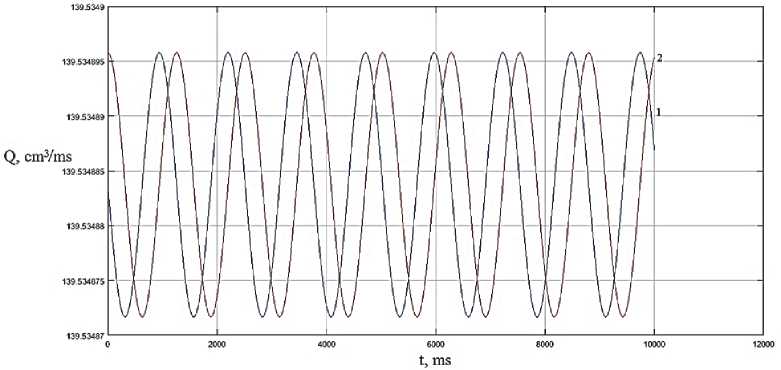
Рис. 8. Динамика изменения расхода при значении частоты го m = 5 Hz и фаз 1: у m =п ; 2: у m =п / 2

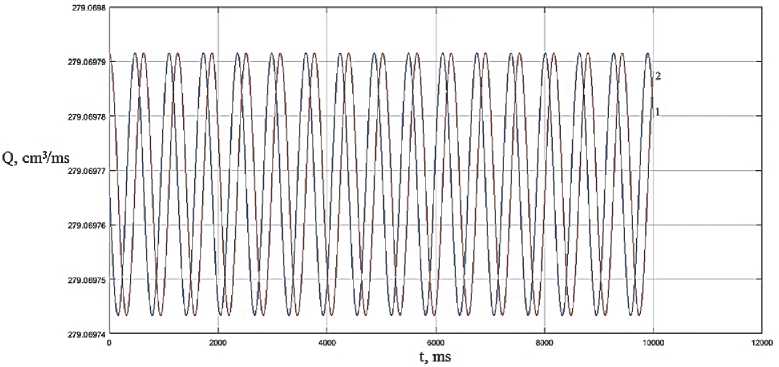
Рис. 9. Динамика изменения расхода при значении частоты го m = 10 Hz и фаз 1: у m = п ; 2: у m =п / 2

Моделирование сигнала управления в качестве синусоиды значительно упрощает частотное регулирование рабочих параметров магнитореологических и магнитодинамических устройств. На рис. 8–11 представлена динамика изменения расходных характеристик при фазовом регулировании. Очевидно, что динамические электромагнитные управляющие поля, в зависимости от частоты, имеют выраженную нестабильность расходных характеристик (см. рис. 8, 9). Борьба с данной нестабильностью возможна путем частотно-фазовой модуляции (см. рис. 10–11). Хорошей стабильности расходных характеристик и общей динамики устройств можно добиться повышением частот управляющих полей и увеличением числа фаз блоков электромагнитного управления. Для магнитодинамических насосов оптимизация частотно-фазовых параметров базируется на предпочтительных или предельно допустимых значениях пульсации расходных характеристик. Рациональное повышение рабочих частот электромагнитного поля, в пределах допустимых значений исходя из времени, необходимого для сохранения релаксационных процессов частиц рабочей среды, а также увеличение количества фаз, число которых должно быть кратным трем, позволяют оптимизировать рабочие процессы магнитодинамических устройств. В случае магнитореологических устройств частотно-фазовые параметры выбираются путем согласования соотношения вязкостных и частотных характеристик. Повышение вязкости магнитореологической среды приводит к росту гидродинамического трения, высоким энергетическим потерям и снижению скоростных параметров потока.

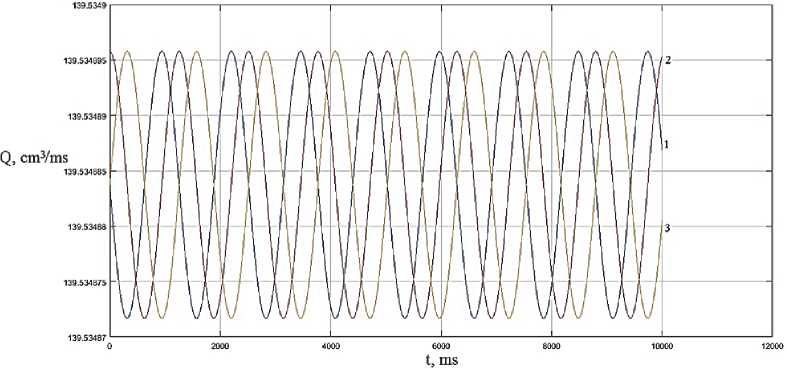
Рис. 10. Динамика изменения расхода при значении частоты

Ю m = 5 Hz и фаз 1: у m = п ; 2: у m =п / 2; 3: у m = 0

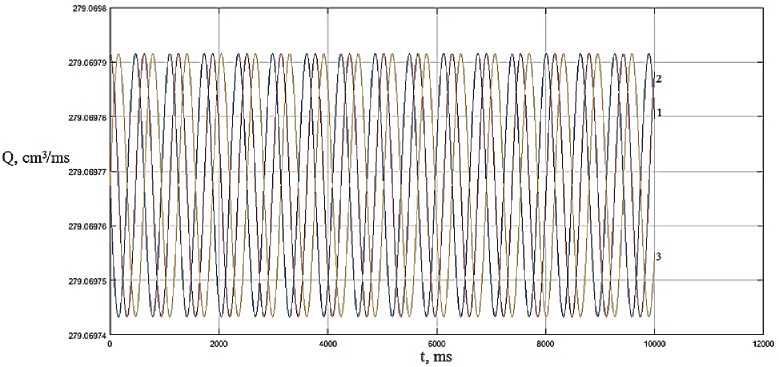
Рис. 11. Динамика изменения расхода при значении частоты го m = 10 Hz и фаз 1: у m =п ; 2: у m =п / 2; 3: у m = 0

Предложенный способ – частотно-фазовый способ оптимизации эффективен и промышленно применим. Параметр скорости изменения спиральности потока является хорошей качественной и количественной характеристикой вихревого течения потока магнитореологической среды.

Новизна. Разработан способ регулирования характеристик магнитореологических приводных систем, отличающийся от ранее известных тем, что для управления потоком рабочей среды применен комбинированный тип управления, реализованный за счет изменения вязкости и генерирова- ния гидродинамических и реологических эффектов во вращающихся и винтовых управляющих электромагнитных полях. Произведена параметрическая оптимизация предложенного способа регулирования характеристик магнитореологических приводных систем по частотно-фазовому принципу с учетом параметра скорости изменения спиральности потока магнитореологической среды.

Выводы

Оптимизация рабочего процесса магнитореологических устройств, применяющих вращающиеся и винтовые управляющие электромагнитные поля по частотно-фазовому принципу, рациональна и высокоэффективна.

Предложенный способ позволяет улучшить динамику и глубину регулирования магнитореологических приводных систем.

При оптимизации рабочих характеристик магнитореологических устройств, применяющих вращающиеся и винтовые управляющие электромагнитные поля, целесообразно рассмотрение параметра – спиральность потока.