Параметрический синтез динамических звеньев для вариантов их включения между нелинейной частью и нагрузкой автоматических систем радиоуправления с общей обратной связью

В работе [1] предложен алгоритм параметрического синтеза динамических звеньев [2] автоматических систем радиоуправления [3] в виде согласующих смешанных четырехполюсников (ССЧ), оптимальных по критерию обеспечения заданных характеристик различных усилительных звеньев с учетом наличия нелинейной части, состоящей из нелинейного элемента (НЭ) и охватывающей его обратной связи.

Цель работы состоит в расширении функциональных возможностей усилительных звеньев путем включения дополнительной цепи обратной связи (ЦОС), охватывающей и нелинейную часть и ССЧ.

Для достижения этой цели делается попытка определить минимальное количество и значения параметров ССЧ, при которых обеспечиваются заданные формы АЧХ и ФЧХ (зависимости модуля m и фазы ф передаточной функции H от частоты) усилительных звеньев с дополнительной общей обратной связью в одном из режимов работы НЭ (аргументы опущены):

H = m (cos ф + j sin ф ). (1)

Для составления исходных уравнений, удовлетворяющих (1), выделим в явном виде нелинейную часть (НЧ), которая может быть выполнена из трехполюсного нелинейного элемента с обратной связью или без нее, цепь прямой передачи (ЦПП) из НЧ и ССЧ, а также общую ЦОС сопротивления источника сигнала z 0 = 1 q + jx 0 и нагрузки z н = ^r H ^{+ jx} н (Рис. 1, 2).

1. Алгоритм параметрического синтеза

Для отыскания передаточных функций исследуемых радиоустройств используем известные правила применения матриц различных параметров для описания четырехполюсников и их соединений, а также условия нормировки общей матрицы передачи узла «НЧ–ЦОС–ССЧ» [4; 5]. Тогда передаточную функцию для структуры с параллельной по напряжению ЦОС, показанной на рис. 1, а , можно записать в следующем виде:

_гг              z ^ [ У OC ( db y + a y b ) + 1 ]

H =---------------------------------------------- ,        (2)

aA o + bB 0 + cC o + dD 0 + ( ad - bc ) E 0 + H 0

где

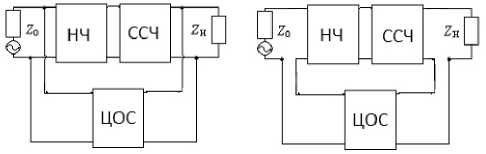
Рис. 1. Структурные схемы усилительных звеньев с параллельной по напряжению ( а ), последовательной по току ( б ) общими цепями обратной связи и ССЧ

Fig. 1. Structural diagrams of amplifying links with parallel voltage ( a ), series current ( b ) common feedback circuits and SFS

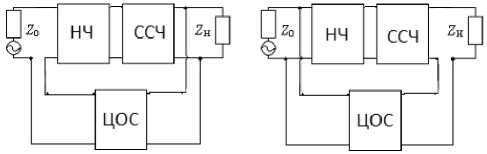
Рис. 2. Структурные схемы усилительных звеньев с последовательной по напряжению ( а ), параллельной по току ( б ) общими цепями обратной связи и ССЧ

Fig. 2. Structural diagrams of amplifying links with serial voltage ( a ), parallel current ( b ) common feedback circuits and SFS

A 0 = ^z^ ^[ c y z 0 + a y ( 1 + y oc z 0^)] ;

B 0 = ^{[ y} tty 2л² 0 ^z^ + ( 1 + ^y Viz 0 ^{)(1 y} 2 ^{c Z}^ ^)] a y + B 01 ^;

B 01 = ^cy^z 0⁽¹ - ^{y oc Z}^ ) ^;

C 0 = ^z^ ^[ d y ^z 0 + b y ⁽¹ + ^y oc z 0^)];

D o = ^{[ y} oc y oc z 0 ^z^ + ⁽¹ + ^y oc z 0⁾⁽¹ - ^y 2 2 ^z^ ^)] b y + D 01 ^;

D 01 = d y z 0^{(1 y 2} 2 ^z^ ) ^;

E 0 = ^- y 2 c^z 0 ^z^ ⁽ a y d y - b y c y ) ;

H oc

0 = ^y 12 ^z 0 ^z^ ;

a y , b y , C y , d y - известные зависимости комплексных элементов классической матрицы передачи НЧ от частоты; y ОС , y 2C , y 21 , y 2 2 - известные зависимости элементов матрицы проводимостей ЦОС от частоты; a , b , c , d – искомые зависимости комплексных элементов классической матрицы передачи ССЧ.

Если положить yОС = 0, y22 = 0, y22 = 0, y22 = 0, то предлагаемый алгоритм синтеза оказывается справедливым и для усилительных динамических звеньев без ЦОС [1]. При синтезе ССЧ без ЦОС и НЧ надо дополнительно принять ay = 1, by = 0, Cy = 0, dy = 1. Если (1) означает обеспечение квазилинейного склона зависимости модуля передаточной функции от частоты, излагаемый материал применим и для синтеза высокочастотной части демодуляторов сигналов с угловой модуляцией.

Подставим (2) в (1). Получим комплексное урав- нение, решение которого приводит к взаимосвязи элементов классической матрицы передачи ССЧ, оптимальной по критерию (1):

,  (Cc + B )b + Da + Cc + C d = —1---------1----2----

C 1 a + D

D = D о M - b y y ^{О2 z}^ = d r + jd x ;

D 1 = ^- A 0 M = ^d 1 r + ^jd 1 _x .

При использовании последовательной по току ЦОС (рис. 1, б ) передаточную функцию можно представить следующим образом:

z [ z ₂₁ ( ac + cd ) + 1 ]

H =-------- —--^y---^y -----------,     (4)

aA₀ + bB ₀ + cC ₀ + dD ₀ + ( ad - bc ) E ₀ + H ₀

где

A о = [( z о + z OC )( z ^ - z OC ) + z 2 2 z 2 C ]C y + a y ( z ^ - z 22) ;

B о = a y ^{+ C}y ^{( z} о ^{+ z} и ) ; H о = z ² 2 ;

C о = [( z о + z OC )( z ^ - z 2 2 ) + z 2 2 z 2 C ] d y + b y ( z ^ - z 2 2 ) ;

D O = b y ⁺ d y ^{( z} 0 ^{+ z} H ) ; E 0 = ^{- z 22 (} a y d y ^- b y^Cy ) ;

z OC , ^z 2 2 , ^z2 C , ² 2 2 — известные зависимости элементов матрицы сопротивлений ЦОС от частоты.

Взаимосвязь между элементами классической матрицы передачи ССЧ, оптимальную по критерию (1), можно также представить в форме (3), но при следующих уточнениях:

B = - B 0 M = b r + jb x ;                               (5)

C = ^z^ ^- H 0 M = ^Cr ^{+ jC}x ; C 1 = E 0 M = ^C 1 r ^{+ jC} 1 x ;

C 2 = ^dy^z^^z 21 ^- C O M = ^C 2 r ^{+ jC} 2 x ^;

D = D ₀ M = d r + jd x ;

D 1 = У у ² н 2 21 ^- A O M = ^d 1 r ^{+ jd} 1 x .

При использовании последовательной по напряжению ЦОС (рис. 2, а ):

z _H [ h 2C ( bC _v+ dd _v) + 1 ]

H =_________^ 21 y____y_____________ aAo + bBо + cco + dDо + (ad - bC)Eо + Hо , где где

B = a y y 2 ^{2 z}^ ^- B 0 M = ^br ^{+ jb}x ;

C = z ^ - H 0 M = C r + jC x ;

C 1 = E 0 M = ^C 1 r ^{+ jC} 1 x ;

C 2 = ^- C 0 M = ^C 2 r ^{+ jC} 2 x ;

A o = ^z^ ^{[ a}y ^{+ c}y ^{( z} o ⁺ h n^)] ;

^H 0 = h ² 2 ^z ^ ^;

B o = B 01 + C y [( 1 - h O2 z ^ )( z o + h 2 ^Cc ) + h O ₂ ^C h 2 2 z ^ ] ;

B 01 = ^{(1 -} h 22 ^z^ ) ^ay ^;

а

б

в

б

в

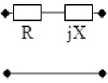
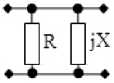
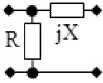
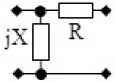
Рис. 3. Примеры синтезированных ССЧ с двумя двухполюсниками

Fig. 3. Examples of synthesized SFSs with two two-terminal networks

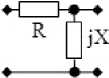
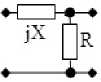
Рис. 4. Примеры синтезированных ССЧ с двумя двухполюсниками (продолжение)

Fig. 4. Examples of synthesized SFSs with two two-terminal networks (continued)

C 0 = z ^ [ b y + d y ( z 0 + h oc )] ;

D 0 = D 01 + d y [( 1 - h )( z 0 + h oc ) + h 1 ⁰ 2 ^C h o 1 ^C z ^ ] ;

D 01 = ^{(1 -} h o 2 ^z^ ) b y ^; E 0 = h o1 ^z н ⁽ a y d y ^{- b}y^cy ) ^;

h oc >  h oc >  h oc >  h oc — известные зависимости элементов смешанной матрицы H ЦОС от частоты.

Коэффициенты для взаимосвязи (3) между элементами классической матрицы передачи ССЧ,

оптимальной по критерию (1):

B = C y h 2 ^o 1 ^c z ^ - B 0 M = b r + jb x ;

C = ^z^ - H 0 M = ^cr ^{+ jc}x ;

C 1 = E 0 M = ^c 1 r ^{+ jc} 1 x ;

C 2 = ^- C 0 M = ^c 2 r ^{+ jc} 2 x ^;

D = D 0 M ^{- d}y^z^^h12 1 = d r + jd x ^;

D 1 = ^- A 0 M = d 1 r + ^j d 1 x .

При использовании параллельной по току ратной связи (рис. 1, г ):

_H=           z^ [ f oc ( aa y + b y c ) + 1 ]

aA ₀ + bB ₀ + cC ₀ + dD ₀ + ( ad - bc ) E ₀ + H ₀ ’

об-

где

A 0 = ^[ f l oc f oc z 0 + ⁽¹ + f H z 0^{)( z}^ - f oc ^)] a y + A 01 ;

A 01 = ^cy^z 0 ^{( z}^ - f oc ) ; B 0 = a y ⁽¹ + f Hz 0^)] + ^z 0 ^cy ;

C 0 = ^[ f oc f oc z 0 + ^{( z}^ - f 22 ⁾⁽¹ + f oc z 0^)] b y + C 01 ;

C 01 = d y z 0^{( z}^ - f oc ) ; D 0 = d y z 0 + b y ⁽¹ + f oc z 0 ) ;

E 0 = f oc ^z0⁽ a y d y - b y c y ) ; H 0 = f oc z 0 ;

f oC , f oc , f oc , f oc — известные зависимости элементов смешанной матрицы F ЦОС от частоты.

Коэффициенты для взаимосвязи (3) для этого варианта:

B = - B 0 M = b r + jb x ;                               (9)

C = ^z^ ^- H 0 M = ^Cr ^{+ jC}x ; C 1 = E 0 M = ^c 1 r ^{+ jc} 1 x ;

C 2 = b y z H f ol - C 0 M = ^c 2 r ^{+ jc} 2 x ^;

D = D ₀ M = d r + jd_x ;

D 1 = a y z u f o ^- A 0 M = ^d 1 r ^{+ jd} 1 x .

Для отыскания выражений для определения параметров типовых схем ССЧ необходимо найти эле-

менты a , b , c , d [4; 5], выраженные через сопротивления или проводимости двухполюсников, а также коэффициенты B , C , C 1 , C 2 , D , D 1 с выбранным типом обратной связи и подставить их в (3). Затем это комплексное уравнение надо разделить на действительную и мнимую части и решить полученную таким образом систему двух алгебраических действительных уравнений относительно сопротивлений или проводимостей двух двухполюсников выбранной схемы ССЧ. В результате получаются зависимости сопротивлений резистивных и реактивных двухполюсников от частоты, оптимальные по критерию (1). Задача реализации этих частотных характеристик в ограниченной полосе частот решена в работе [4].

2. Результаты параметрического синтеза

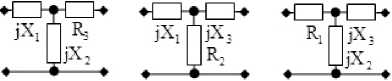
Здесь приводятся некоторые из решений, полученных для типовых схем ССЧ при использовании варианта структурной схемы с параллельной по напряжению обратной связью (рис. 1, а ). Если в качестве ССЧ используется последовательно включенные резистивный двухполюсник с сопротивлением R и реактивный двухполюсник с сопротивлением jX (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом:

R =

^{( c}r ^{- c} 1 r ^- d r ^{+ d} 1 r ) b r ^{+ ( c}x ^{- c} 1 x ^{- d}x ^{+ d} 1 x ) b x .

- ( b r ² + b x )

X =

^{( c}x ^{- c} 1 x ^- d x ^{+ d} 1 x ^{) b}r ^{- ( c}r ^{- c} 1 r ^- d r ^{+ d} 1 r ) b x

- ( b r ² + b x ² )

ССЧ в виде параллельно включенных двухполюсников R и jX (рис. 3, б ):

- ( c ² + c ² ) ^{2 r 2 x}                        ; (11)

^{( c}r ^{- c} 1 r ^- d r ^{+ d} 1 r ) ^c 2 r ^{+ ( c}x ^{- c} 1 x ^- d x ^{+ d} 1 x ) ^c 2 x

_____________________ ^{-( c} 2 r ^{+ c 2} x ) _____________________

^{( c}r ^{- c} 1 r ^- d r ^{+ d} 1 r ) ^c 2 x ^{- ( c}x ^{- c} 1 x ^- d x ^{+ d} 1 x ) ^c 2 r

ССЧ в виде Г-образного соединения двухполюсников R и jX (рис. 3, в ):

R ₌        С 2 r + Xd x       ;

c 1 r ^- c r + d r ^- d l r + Xb x

X _- X 0 + ⁽ c x - c l x - d x + d l x ^{) d} _X + b r c 2 r + b x c 2 x - Q - 2 ( b r d x - b x d r )                  ’

X 0 ^{- (} c r ^{- c} l _r ^- d r + ^d _{l r} ) d r ;

^Q = ± У ^[( c r ^- c i _r - d r + d i _r ) d r +

^{+ (} c x ^- c 1 x ^- d x ⁺ d l x ) d x ⁺ b r ^c2 r ⁺ b x ^c2 x ^]2 - Q 0^;

^Q 0 ^{- 4[(} c x ^{- c} 1 x ^- d x ⁺ d l x ) ^c 2 r ^-

^{- (} c r ^- c l r ^- d r + d l r ) c 2 x ^{] Q} 1^;

Q l = ( b r d x - b x d r ) .

ССЧ в виде Г-образного соединения двухполюсников jX и R (рис. 4, а ):

_{R -} ^c 2 r ⁺ X ^{( c} l x ^- c x ⁺ d x - d l x ) .                      (_l3)

d r + Xbx         ’

X _- X 0 ^{+ (} c x ^{- c} l x ^- d x ⁺ d l x ) d x ⁺ b r c 2 r ⁺ b x c 2 x ^- Q ;

^{- 2[} b r ⁽ c l x ^- c x ⁺ d x - d l x ) ⁺ b x ⁽ c r ^{- c} l r ^- d r ⁺ d l r ^)]

X 0 ^{- (} c r ^- c _{l r} ⁺ d _{l r} ^- d r ) d r ;

Q= ± V [( c_r - c _{l r} - d_r + d l _r ) d_r +

^{+ (} c x ^- c l x ^- d x ⁺ d l x ) d x ⁺ b r c 2 r ⁺ b x c 2 x ^{]2 -} Q 0^;

^Q 0 ^{- 4[} b r ⁽ c x ^- c l x ^- d x ⁺ d l x ) ⁺

⁺ b x ⁽ c l r ^- c r ⁺ d r ^- d l r ^)]2 "

ССЧ в виде обратного Г-образного соединения двухполюсников R и jX (рис. 4, б):

X ⁽ c x ^- c l x ⁺ d l x ^- d x ) ^- c 2 r d l r - Xb x          ’

X 0 ^{+ (} c x ^- c l x ^- d x ⁺ d l x ^{) d} l x ^- b r c 2 r ^- b x c 2 x ⁺ Q ;

^2[ b x ⁽ c r ^- c l r ^- d r ⁺ d l r ) ⁺ b r ⁽ c l x ^- c x ⁺ d x ^- d l x ^)]

X 0 - ⁽ c r ^- c l r ^- d r ⁺ d l r ) d l r ;

Q ^- ± V ^[( c l x ^- c x ⁺ d x ^- d l x ^)d l x ⁺

^{+ (} c l r ^- c r ^{+ d}r ^{- d} l r ) ^d l r ⁺ b r c 2 r ⁺ b x c 2 x ^{] 2 -} Q 0^;

^Q 0 ^{- 4[} b x ⁽ c r ^- c l r ^- d r ^{+ d} l r ) ^-

^- b r ⁽ c x ^- c l x ^{- d}x ^{+ d} l x ^)](c2 r ^d l x ^{- c}2 x ^d l r )•

^Q 0 ^{- 4[c}2 r ⁽ c x ^- c l x ^{- d}x ^{+ d} l x ) ^-- c 2 x ⁽ c r ^- c l r ^- d r ^{+ d} l r ^{)] Q} 0l ;

^{+ (} c l r ^- c r ^{- d} l r ^{+ d}r ) ^d l r ⁺ b r c 2 r ⁺ b x c 2 x ^{] 2 +} Q 0 S

X 0 ^{- (} c l x ^- c x ^{+ d}x ^{- d} l x ) ^d l x ;    Q 0l ^- b r d l x ^- b x d l r .

ССЧ в виде Т-образного соединения двухполюсников jX ₁ , jX ₂ и R ₃ (рис. 5, а ). При выборе комбинации X l , X 2 имеем:

X _l -

- B _l ± JB 2 - 4 A _l C _l

2 A ₁

X ₂ -

- B 2 ± д/ b 22 - 4 A 2 C 2 2 A ₂

где

A l - R 3 ( b r ² + b x ² ) + b r d l r + b x d l x ;

B l ^{- ( d} l x ⁺ R 3 b x ⁾⁽ c l r ^- c r ⁺ d r ) ^-

^{- ( d} l r ⁺ R 3 b r ⁾⁽ c l x ^- c x ⁺ d x ) ⁺

⁺ b r ⁽ c 2 x ^- R 3 ^dx ) ^- b x ⁽ c 2 r ^- R 3 d r ) ;

C l ^{- (} c_r ^- c l _r ^{- d} _r ⁺ d l _r ⁾⁽ c 2 _r ^- R 3 ^d _r ) ⁺

⁺ R 3⁽ b r c 2 r ⁺ b x c 2 x ) ^- R 3⁽ b r d r ⁺ b x d x ) ⁺

^{+ (} c 2 x ^- R 3 ^dx ⁾⁽ c x ^- c l x ^{- d}x ^{+ d} l x ) ;

A 2 ^- R 3⁽ b ^{2 +} b x ) ^{+ (} c x ^- c l x ^{- d}x ^{+ d} l x ) b x ⁺

^{+ (} c r ^- c l r ^- d r ^{+ d} l r ) b r ^;

B 2 ^{- ( d} l x ⁺ R 3 b x ⁾⁽ c r ^- c l r ) ^{- ( d} l r ⁺ R 3 b r ⁾⁽ c x ^- c l x ) ⁺

⁺ b r c 2 x ^- b x c 2 r ^{- d}r^d l x ^{+ d}x^d l r ;

C 2 ^{- c} 2 r^d l r ^{- c} 2 x^d l x ⁺

⁺ R 3⁽ b r c 2 r ⁺ b x c 2 x ^{- d}r^d l r ^{- d}x^d l x ) ^- R 3⁽ b r d r ⁺ b x d x )•

Далее при смене сочетаний по два из общего числа двухполюсников типовых схем ССЧ всюду изменяются коэффициенты A l , B l , C l , A 2 , B 2 , C 2 и смысл сопротивлений X ц X 2 в (l6). При выборе комбинации jX ц R 3 (рис. 5, а ) надо в (l6) положить X l - X l ; X 2 - R 3 >  и изменить указанные коэффициенты: A l - b x d l r - b r d l x - X 2 ( b r ² + b x ² ) ;

B l ^- b r c 2 r ⁺ b x c 2 x ⁺ d r d l r ⁺ d x d l x ^-

ССЧ в виде обратного Г-образного соединения двухполюсников jX и R (рис. 4, в ):

R -

c 2 r Xdl x clr ~ cr + dr - dl r + Xbx

;

X -

X 0 ^{- (} c r ^- c l r ^{+ d} l r ^- d r ) ^d l r ⁺ b r c 2 r ⁺ b x c 2 x ⁺ Q

2(ь -ь a.)

r 1 x     x 1 r

;

^{- X} 2 ⁽ b r ^{+ b} 2 ) ^{+ [} b x ⁽ c r ^{- c} l _r ^{- 2 d} _r ^{+ 2 d} l _r ) ^{+ +} b r ⁽ c l x ^- c x ^{+ 2 d}x ^{- 2 d} l x ^{)] X} 2^;

C l ^{- X} 2^{( d}x ^{- X} 2 b r ⁾⁽ c x ^{- c} l x ^{- d}x ^{+ d} l x ) ^{+ + X} 2⁽ b r c 2 r ⁺ b x c 2 x ) ^{- X} 2^{( d}r ^{- X} 2 b x ) ^{x X (} c l r ^- c r ⁺ d r ^{- d} l r ) ^- c 2 r^dx ⁺ c 2 x^dr ^;

Q ^- ± V ^[( c l x   c x  ^d l x ^{+ d}x ^)d"lx ⁺

A 2 -- ( b r d r + b x d x ) ;

B 2 = ^[ b x ⁽ c r ^- c l r ) + b r ^{( c} 1 x ^- c x ^{)] X} 2 +

+ X 2 ( b 2 + ^b 2 ) + b r C 2 r + b x C 2 x - d r d i r - d x d l x ;

C 2 = ^X 2⁽ d l r ^{- X} 2 b x ⁾⁽ c 1 x ^- c x ⁺ d x ) ^-

• ^- X 2⁽ d i x + X 2 b r ⁾⁽ c i r - c r + d r ) + X 2⁽ b r c 2 x ^- b x c 2 r ) +

• ^{+ X} 2 ⁽ b r d l r ⁺ b x d l x ) ⁺ c 2 r d l r ⁺ c 2 x d l x •

При выборе комбинации jX 2 , R 3 (рис. 5, а ) надо в (16) положить X i = X 2 ; X 2 = R 3 :

• A 1 = b x ⁽ c r ^- c l r ^- d r ⁺ d i r ) ^-

• - br(cx - clx - dx + dlx) - X1(b2 + b2);

B l = ⁽ d x ^{- X} 1 b r ⁾⁽ c x - c 1 x ^- d x ⁺ d l x ) ⁺

^{+ (} d_r ^{+ X} 1 b_x ^{)( c} _r ^- c 1 _r ^- d_r ⁺ d l _r ) ⁺

• ⁺    b r c 2 r ⁺ b x c 2 x ^{- X} 1 ⁽ b r ⁺ b x ) -

• -    X ₁ [( d _{1 x} - d_x ) b_r - ( d _{1 r} - d_r )b_x ];

C l = C 0 ^{+ X} 1⁽ b r c 2 r ⁺ b x c 2 x ⁺

• ^{+    d}r^d 1 r ^{+ d}x^d 1 x ) ^- c 2 r d x ⁺ c 2 x d r ;

C 0 = X l ² ( b x d l r - b r d l x ) ; A 2 =- ( bd + b x d x ) ;

B 2 = d r ⁽ c 1 r ^- c r ^- d l r ⁺ d r ) ⁺ d x ⁽ c 1 x ^- c x ^- d l x ⁺ d x ) ⁺

• ⁺    b r c 2 r ⁺ b x c 2 x ^{+ X 2 (} b r ⁺ b x ) ⁺

+ ^[ b r ⁽ c x ^- c 1 x ^{- 2} d x ) ⁺ b x ⁽ c 1 r ^- c r ^{+ 2} d r ^{)] X} 1 ;

C 2 = ^X 1^[ d l r ⁽ c x ^- c 1 x ⁺ d l x ) ⁺ d l x ⁽ c 1 r ^- c r ⁺ d r ) ⁺

• ⁺    b r c 2 x ^- b x c 2 r ^{] + X} l ^{2 (} b r d l r ⁺ b x d l x ) ⁺

• ⁺    c 2 r ⁽ c r ^- c 1 r ^- d r ⁺ d l r ) ⁺ c 2 x ⁽ c x ^- c 1 x ^- d x ⁺ d l x )•

ССЧ в виде Т-образного соединения двухполюсников jX 1 , jX 3 и R 2 (рис. 5, б ). При выборе комбинации jX ₁ , R 2 в (16) X ₁ = X ₁; X 2 = R 2 :

A l = X з ( ^b 2 + ^b 2 ) + b r d l x - b x d l r ;                      (17)

B l = ⁽ c x ^- c 1 x ^- d x ⁺ d l x ) d l x ⁺

• ^{+    X} 3^[( c x ^- c 1 x ^{- 2} d x ^{+ 2} d l x ) b r ^-

• -    bx (cr - cl r - 2 dr + 2 dlr)] + (cr - cl r - dr + dl r) dl r - -    brc2r - bxc2x + X3(br + b2);

C l = ⁽ c r ^- c l r ^- d r ⁺ d l r ⁾⁽ c 2 x ^{- X} 3 d r ) ^-

• ^{-    X} 3⁽ b r c 2 r ⁺ b x c 2 x ) ^{- X} 3⁽ b r d x ^- b x d r ) ^-

• ^{-    (} c x ^- c l x ^- d x ⁺ d l x ⁾⁽ c 2 r ^{+ X} 3 d x ) ;

A 2 = ⁽ c x ^- c 1 x ^- d x ⁺ d l x ) b x ^{+ (} c r ^- c l r ^- d r ⁺ d l r ) b r ;

B 2 = ^X 3^{( b} 2 ⁺ b x ) ^{+ [(} c x ^- c 1 x ^{+ 2} d l x ) b r ^-

• ^-    b xc ⁽ c r ^- c 1 r ^{+ 2} d l r ^{)] X} 3 ^{+ (} c r ^- c 1 r ^- d r ⁺ d l r ^{) d} 1 r ^-

• ^-    d l x ⁽ c 1 x ^- c x ⁺ d x ^- d l x ) ⁺ b r c 2 r ⁺ b x c 2 x ;

C 2 = ^X 3⁽ b r c 2 x ^- b x c 2 r ^- d r d l x ⁺ d x d l r ) ^-

• ^X 3⁽ b r d r ⁺ b x d x ) ⁺ c 2 r d l r ⁺ c 2 x d l x .

При выборе комбинации jX 1 , jX 3 (рис. 5, б ) надо в (16) положить X 1 = X 1 ; X 2 = X 3 :

A l = R 2 ( ^b 2 + ^b 2 ) + b r d l r + b x d l x ;

B l = b r c 2 x ^- b x c 2 r ⁺ d r d l x ^- d x d l r ⁺

• ⁺ R 2^[( c x ^- c 1 x ^{- 2} d x ^{) b}r ⁺ b x ⁽ c 1 r ^- c r ^{+ 2} d r ^)] ;

C l = ^R 2⁽ b r c 2 r ⁺ b x c 2 x ) ^-

• ^{-    R} 2⁽ d r ^{- R} 2 b r ⁾⁽ c r ^- c 1 r ^- d r ⁺ d l r ) ^-

• ^{-    R} 2⁽ d x ^- R 2 b x ⁾⁽ c x ^- c 1 x ^- d x ⁺ d l x ) ^-

• ^{-    (} c 2 r d r ⁺ c 2 x d x ) ;

A ₂ = R ₂ ( b ² + b 2 ² ) - b_Td_T - b_xd ; r x rr xx

B 2 = b r c 2 x ^- b x c 2 r ⁺ R 2^[ b r ⁽ c x ^- c l x ^{+ 2} d l x ) ^-

• ^-    b x ⁽ c r ^- c l r ^{+ 2} d l r ^{)] +} d x d l r ^- d r d l x ;

C 2 = R 2^[( d l x ⁺ R 2 b x ⁾⁽ c x ^- c 1 x ^- d x ⁺ d l x ) ⁺

• ⁺ b r c 2 r ⁺ b x c 2 x ^{] +} c 2 r d l r ⁺ c 2 x d l x ⁺

+ R 2⁽ d l _r + ^R 2 b_r ⁾⁽ c_r ^- c 1 _r ^- d_r + d l _r ) .

При выборе комбинации R 2 , jX 3 (рис. 5, б ) надо в (16) положить X 1 = R 2 ; X 2 = X 3 :

A 1 = b x ⁽ c x ^- c l x ^- d x ⁺ d l x ) ⁺ b r ⁽ c r ^- c 1 r ^- d r ⁺ d l r ) ;

B l = d x ⁽ c l x ^- c x ^- d l x ⁺ d x ) ⁺ d r ⁽ c l r ^- c r ^- d l r ⁺ d r ) ⁺

+ ^X 2^{( b} 2 + b x ) + b r c 2 r ⁺ b x c 2 x ^- d r d l r ^- d x d l x ⁺

+ X 1^[( c 1 _r ^- c_r + ² d_r ) b_x ^- b_r ⁽ c 1 _x ^- c_x + ² d_x ^)] ;

C l = ^X1⁽ b r c 2 x ^- b x c 2 r ⁺ d r d l x ^- d x d l r ) ^-

• ^- c 2 r d r ^- c 2 x d x ^{+ X} I⁽ b r d l r ⁺ b x d l x ) ;

A 2 = X l ² ( b r + b x ²) - b r d x + b x d , ;

B 2 = ⁽ d x ^{- 2 X} 1 b r ⁾⁽ d x ^{- d} 1 x ) ⁺

^{+ ( d} _r ^{+ 2 X} 1 b_x ^{)( d} _r ^{- d} 1 _r ) ^{- (} c_x ^- c 1 _x ^{)( d} _x ^{- X} 1 b_r ) ^-

22  2

r 2 r    x 2 x      r 1 x r    1 r       1 r x ;

C 2 = ⁽ X 1 d l x ^- c 2 r ⁾⁽ c x ^- c 1 x ^{- d}x ^{+ d} 1 x ) ⁺

^{+ X} 2⁽ b r d l x ^- b x d l r ) ^{- X} 1⁽ b r c 2 r ⁺ b x c 2 x ) ⁺

^{+ (} c 2 _x ^{+ X} 1 ^d 1 _r ⁾⁽ c r ^- c 1 _r ^{- d} _r ^{+ d} 1 _r ) .

ССЧ в виде Т-образного соединения двухполюсников R i , jX 2 , jX 3 (рис. 5, в ). При этом в (16) X ₁ = R ₁ ; X 2 = X 2 :

A l = b r d l r + b x d l x ;                                       (18)

B l = ⁽ c r ^- c 1 r ^{- d}r ^{+ d} 1 r ^{) d} 1 r ^{- d} 1 x ⁽ c 1 x ^- c x ^{+ d}x ^{- d} 1 x ) ⁺

⁺ b r c 2 r ⁺ b x c 2 x ^{+ X} 3^{( b} 2 ⁺ b x ) ⁺

^{+ X} 3^[( c 1 r ^- c r ^{- 2 d} 1 r ) b x ⁺ b r ⁽ c x ^- c 1 x ^{+ 2 d} 1 x ^)] ;

а              б              в

Рис. 5. Примеры синтезированных ССЧ с тремя двухполюсниками

Fig. 5. Examples of synthesized SFSs with three two-terminal networks

а                б               в

Рис. 6. Примеры синтезированных ССЧ с тремя двухполюсниками (продолжение)

Fig. 6. Examples of synthesized SFSs with three two-terminal networks (continued)

C l = ⁽ c 2 x ^X 3 d r ⁾⁽ c x c l x + d l x ) +

+ X 3⁽ b r c 2 x - b x c 2 r ) - X 3⁽ b r d r + b x d x ) -

• -    C 2 r d r - C 2 x d x + ⁽ C 2 r + X з d x ⁾⁽ c r - c l r + d l r ) ;

A 2 = b x ⁽ c r - ^c 1 r - d r ⁺ d l r ) -

• -    b r ⁽ c x - c l x - d x + d l x ) - X 3⁽ b 2 + b x ) ;

B 2 = ⁽ d r - ² X 3 b x ⁾⁽ d r - d l r ) ⁺ b r c 2 r ⁺ b x c 2 x -

• -    ⁽ d l x + X 3 b r ⁾⁽ c x - c l x ) - ⁽ c r - c l r ⁾⁽ d l r - X 3 b x ) -

• - X2(b2 + b2) +(dlx + 2X3br)(dx - dlx);

C 2 = X 3⁽ b r c 2 r ⁺ b x c 2 x ⁺ d r d l r ⁺ d x d l x ) ⁺

^{+ c} 2 r d l x - ^c 2 x d l r ^{+ (} b r d x - b x d r ) X 3 ^.

При выборе комбинации R l , jX 3 (рис. 5, в ) надо в (l6) положить X l = ^ l ; X 2 = X 3 :

A l = b r d l r ⁺ b x d l x ^;

B l = ⁽ b r ⁺ b x ) X 2 ⁺ b r c 2 r ⁺ b x c 2 x ⁺

⁺ X 2^[( c r - c l r ^)bx - b r ⁽ c x - ^c l x ^)] - d r d l r - d x d l x ^;

C l = ^[( c r - c l r - d r ⁺ d l r ) b r ⁺

⁺ b x ⁽ c x - ^c l x - d x ⁺ d l x ^)] X 2 ^{+ [} b r c 2 x - b x c 2 r ⁺

^{+ (} c x - ^c l x ⁺ d l x ^{) d}r - d x ⁽ c r - c l r ⁺ d l r ^)] X 2 -

• -    c 2 r d r - c 2 x d x ;

A 2 = b r d x - b x d r - X 2⁽ b ^{2 +} b ² ) ;

B 2 = X 2^[( c l x - c x ^{+ 2} d x - ² d l x ) b r - ⁽ b r ⁺ b x ) X 2 ⁺

• ⁺    b x ⁽ c r - c l r - ² d r ^{+ 2} d l r ^{)] +}

• ⁺    b r c 2 r ⁺ b x c 2 x ⁺ d r d l r ⁺ d x d l x ;

C 2 = ⁽ b r c 2 r ⁺ b x c 2 x ) X 2 -

• - X 2⁽ d l r - X 2 b x ⁾⁽ c r - c l r - d r ⁺ d l r ) -

  - X 2⁽ d l x ⁺ X 2 b r ⁾⁽ c x - c l x - d x ⁺ d l x ) ⁺ c 2 r d l x - c 2 x d l r ^.

При выборе комбинации jX 2 , jX 3 (рис. 5, в ) надо в (l6) положить X l = X 2 ; X 2 = X 3 :

A l = ⁽ b 2 ⁺ b x ) R l ^{+ (} c_r - c l _r - d_r ⁺ d l _r ) b_r ⁺

• ⁺    b x ⁽ c x - c l x - d x ⁺ d l x ) ;

B l = ⁽ R l b x - d x ⁾⁽ c r - c l r ) ^{+ (} d r - R l b r ⁾⁽ c x - c l x ) ⁺

• ⁺    b r c 2 x - b x c 2 r ⁺ d r d l x - d x d l r ;

C l = R 2⁽ b r d l r ⁺ b x d l x ) ⁺

• ⁺ R l⁽ b r c 2 r ⁺ b x c 2 x - d r d l r - d x d l x ) - c 2 r d r - c 2 x d x ;

A 2 = R l⁽ b 2 ⁺ b 2 ) - brdr - bxdx ; r x rr xx

B 2 = ⁽ c l x - c x - d x ^{) d}r ⁺ b r c 2 x - b x c 2 r ⁺

⁺ R l^[( c x - c l x ^{+ 2} d l x ^{) b}r - b x ⁽ c r - c l r ^{+ 2} d l r ^{)] +}

⁺ d x ⁽ c r - c l r ⁺ d l r ) ;

C 2 = ⁽ c 2 x ⁺ R l d l x ⁾⁽ c x - c l x - d x ⁺ d l x ) ⁺

^{+ (} c 2 _r ⁺ R l d l _r ⁾⁽ c_r - c l _r - d_r ⁺ d l _r ) ⁺

+ R l ( b r C 2 r + b x C 2 x ) + R 2 ( b r d l r + b x d l x ) .

ССЧ в виде П-образного соединения двухполюсников jX l , jX 2 и R 3 (рис. 6, а ). При этом в (l6) X l = X l ; X ₂ = X ₂ :

A l = ^[( d l x ^{+ R} 3 b x ⁾⁽ c x - c l x - d x ⁺ d l x ) ^{+                (l9)}

⁺ b r c 2 r ⁺ b x c 2 x ^{] R} 3 ^{+ [(} d l r ^{+ R} 3 b r ) ^X

^{X (} c r - c l r - d r ⁺ d l r ^{)] R} 3 ⁺ c 2 r d l r ⁺ c 2 x d l x ;

B l = ^[( c l r - c r - d l r ^)dx ⁺ d r ⁽ c x - c l x ⁺ d l x ) ⁺

⁺ b r c 2 x - b x c 2 r ^{] R} 3 ^{+ [(} c r - c l r ^{+ 2} d l r ^{) c} 2 x -

• -    c 2 r ⁽ c x - c l x ^{+ 2} d l x ^{)] R} 3 ;

C l = ^R 3⁽ c 2 r ⁺ c 2 x ) - ^R 3⁽ c 2 r d r ⁺ c 2 x d x ) ^;

A 2 = ⁽ b r c 2 r ⁺ b x c 2 x - d r d l r - d x d l x ) ^R 3 -

• -    ⁽ b r d r ⁺ b x d x ) ^R 3 ⁺ c 2 r d l r ⁺ c 2 x d l x ;

B 2 = ^[( c x - c l x ) c 2 r ^{+ (} c l r - c r ) c 2 x ^{] R} 3 ⁺

• ^{+ R} 3 [ b r c 2 x - b x c 2 r ⁺ d r ⁽ c l x - c x - d l x ) ⁺

+ d_x ( c_r - c _l r + d _{l r} )] ;

C 2 = ^[( c x — c l x — d x ⁺ d l x ) c 2 x ⁺

⁺ c 2 r ⁽ c r ^- c l r ^- d r ⁺ d l r ^{)] R} 3 ^{+ R} 3⁽ c 2 r ⁺ c 2 x ) •

При выборе комбинации jX _l , R ₃ (рис. 6, а ) надо в (l6) положить X l = X l ; X 2 = R 3 :

A l = ^(c2 x ^{+ X} 2 d l r ⁾⁽ c r ^- c l r ^- d r ⁺ d l r ) ⁺

^{+ X} 2 ⁽ b r d l x ^- b x d l r ) - ^X 2⁽ b r c 2 r ⁺ b x c 2 x ) -

- ⁽ c 2 r - X 2 ^d 1 x ⁾⁽ c x - ^c 1 x - d x + ^d 1 x ) ;

B 1 = X 2^{[( c} 1 x - c x + ² d x - ^{2 d} 1 x ^)c 2 r +

+ c 2 x ⁽ c r - c 1 r - ² d r + ^{2 d} 1 r ^)] -

- X 2 ⁽ b r c 2 r + b x c 2 x + dd r + d x d i x ) + C 2 r + C 2 x ;

C 1 = X 2⁽ c 2 r ⁺ c 2 x ) ⁺ X 2 ^{( c} 2 r d x - ^c 2 x d r ) ;

A 2 = ^[( c 1 x - c x - ^d 1 x ) d r ⁺ d x ⁽ c r - c 1 r ^{+ d} 1 r ) ⁺

⁺ b r c 2 x - b x c 2 r ^] X 2 - ⁽ b r d r ⁺ b x d x ) X 22 ⁺

^{+ (} c r - ^c 1 r - d r ^{+ d} 1 r ) ^c 2 r ^{+ c} 2 x ⁽ c x - ^c 1 x - d x ^{+ d} 1 x ) ;

B 2 = ⁽ b r c 2 r ⁺ b x c 2 x - d r^d 1 r - ^dx^d 1 x ) X 2 ^{+ c} 2 r ^{+ c} 2 x -

- ^[( c r - ^c 1 r ) ^c 2 x - ^c 2 r ⁽ c x - ^c 1 x ^)] X 2 ;

C 2 = ^{( c} 2 r^d 1 r ^{+ c} 2 x^d 1 x ) X 2 ^.

При выборе комбинации jX 2 , R 3 (рис. 6, а ) надо в (16) положить X 1 = X 2 ; X 2 = R 3 :

A 1 = X 2⁽ b r^d 1 x - b x^d 1 r ) - X 1⁽ b r c 2 r ⁺

• ⁺ b x c 2 x ⁺ d r^d 1 r ⁺ d x^d 1 x ) ⁺ c 2 r d x - c 2 x d r ;

B 1 = ^[( c 2 _x ^{+ d} 1 _r ^X 1⁾⁽ c_r - c 1 _r - ^d _r ^{+ d} 1 _r ) -

• - ⁽ c 2 r - ^d 1 x^X 1⁾⁽ c x - c 1 x - d x ^{+ d} 1 x ^)] X 1 -

• - X2(brc2r + bxc2x) - X1[c2x(dr - d1 r) -

  - c2 r⁽dx - ^d1 x^{)] +}c2 r⁺c2 x ;

C 1 = ^[( c 1 x - c x ⁺ d x - ^d 1 x ) c 2 r ⁺

⁺ c 2 x ⁽ c r - c 1 r - d r ^{+ d} 1 r ^)] X 2 ⁺ X 1⁽ c 2 r ⁺ c 2 x ) ;

A 2 = ^[( c x - c 1 x - d x ^{+ d} 1 x ) b x ⁺

⁺ b r ⁽ c r - c 1 r - d r ^{+ d} 1 r ^)] X 2 - c 2 r d r - c 2 x d x ⁺

^{+ [(} c 1 r - c r - ^d 1 r ) d x ⁺ d r ⁽ c x - c 1 x ^{+ d} 1 x ) ⁺

⁺ b r c 2 x - b x c 2 r ^] X 1 ;

B 2 = ^[( c x - c 1 x - d x ^{+ d} 1 x ) ^d 1 x -

- ^d 1 r ⁽ c 1 r - c r ⁺ d r - ^d 1 r ) ⁺ b r c 2 r ⁺ b x c 2 x ^] X 2 ⁺

⁺ c 2 r ⁺ c 2 x ^{+ [(} c 1 x - c x - ^{2 d} 1 x ) c 2 r ⁺

⁺ c 2 x ⁽ c r - c 1 r ^{+ 2 d} 1 r ^)] X 1 ;

C 2 = ⁽ c 2 r^d 1 r ⁺ c 2 x^d 1 x ) X 2 .

ССЧ в виде П-образного соединения двухполюсников jX 1 , R 2 и jX 3 (рис. 6, б ). При выборе комбинации jX 1 , R 2 в (16) надо положить X 1 = X 1 ; X 2 = R 2 : A 1 = ^X 3^{[( d} 1 _r - ^X 3 b x ⁾⁽ c r - c 1 _r - d r ^{+ d} 1 _r) ^{+             (20)}

^{+ ( d} 1 x ^{+ X} 3 b r ⁾⁽ c x - c 1 x - d x ^{+ d} 1 x ^)] -

- ^X 3⁽ b r c 2 r ⁺ b x c 2 x ) - c 2 r^d 1 x ⁺ c 2 x^d 1 r ;

B 1 = c 2 r ⁺ c 2 x ^{+ [} c 2 r ⁽ d x - ^d 1 x ) - c 2 x ⁽ d r - ^d 1 r ^{)] X} 3 ⁺

^{+ [(} c 2 x - d r^X 3⁾⁽ c r - c 1 r - d r ^{+ d} 1 r ) -

• -    ⁽ c 2 r ^{+ d}x^X 3⁾⁽ c x - c 1 x - d x ^{+ d} 1 x ^)] -

• -    X 3⁽ b r c 2 r ⁺ b x c 2 x ) ;

C 1 = ^X 3⁽ c 2 r ⁺ c 2 x ) ^{+ X} 3⁽ c 2 r d x - c 2 x d r ) ^;

A 2 = - ^X 3⁽ b r d r ⁺ b x d x ) ^{+ X} 3⁽ b r c 2 x - b x c 2 r -

• - d r^d 1 x ^{+ d}x^d 1 r ) ⁺ c 2 r^d 1 r ⁺ c 2 x^d 1 x ;

B 2 = ^X 3⁽ b r c 2 r ⁺ b x c 2 x ) ⁺

^{+ [(} c 1 x - c x ^{+ 2} d x ) c 2 r - c 2 x ⁽ c 1 r - c r ^{+ 2} d r ^{)] X} 3 ⁺

⁺ c 2 r ⁺ c 2 x ^{+ X} 3 ^[( c 1 x - c x - ^d 1 x ⁺ d x ) d x ⁺

⁺ d r ⁽ c 1 r - c r - ^d 1 r ⁺ d r ^)] ;

C 2 = ^X 3^[( c r - c 1 r - d r ^{+ d} 1 r ) c 2 r ⁺

⁺ c 2 x ⁽ c x - c 1 x - d x ^{+ d} 1 x ^)] .

При выборе комбинации jX ₁ , jX ₃ в (16) надо по-дожить X 1 = X 1 ; X 2 = X 3 (рис. 6, б ):

A 1 = ⁽ c 2 x ^{+ R} 2 ^d 1 x ⁾⁽ c 1 x - c x ⁺ d x - ^d 1 x ) -

- ^R 2⁽ b r c 2 r ⁺ b x c 2 x ) - ^R 2 ⁽ b r^d 1 r ⁺ b x^d 1 x ) -

- ⁽ c 2 r ^{+ R} 2 ^d 1 r ⁾⁽ c r - c 1 r - d r ^{+ d} 1 r ) ;

B 1 = ⁽ b x c 2 r - b r c 2 x - d r^d 1 x ⁺ d x^d 1 r ) ^R 2 ⁺

⁺ R 2^[( c x - c 1 x ^{+ 2 d} 1 x ) c 2 r - c 2 x ⁽ c r - c 1 r ^{+ 2 d} 1 r ^)] ;

C 1 = ^R 2 ⁽ c 2 r d r ⁺ c 2 x d x ) - R 2⁽ c 2 r ⁺ c 2 x ) ^;

A 2 = ⁽ c 2 x - ^R 2 d x ⁾⁽ c x - ^c 1 x - d x ^{+ d} 1 x ) ⁺

⁺ R 2⁽ b r c 2 r ⁺ b x c 2 x ) - R 2 ⁽ b r d r ⁺ b x d x ) ⁺

^{+ (} c 2 r - ^R 2 d r ⁾⁽ c r - c 1 r - d r ^{+ d} 1 r ) ;

B 2 = ⁽ b r c 2 x - b x c 2 r - ^dr^d 1 x ^{+ d}x^d 1 r ) R 2 ⁺

^{+ [(} c r - c 1 r - ² d r ) c 2 x ⁺ c 2 r ⁽ c 1 x - c x ^{+ 2} d x ^{)] R} 2 ;

C 2 = R 2 ⁽ c 2 r^d 1 r ⁺ c 2 x^d 1 x ) ^{+ R} 2⁽ c 2 r ⁺ c 2 x ) ^.

При выборе комбинации R ₂ , jX ₃ в (16) надо по-дожить X 1 = R 2 ; X 2 = X 3 (рис. 6, б ):

A 1 = ⁽ b x c 2 r - b r c 2 x - ^dr^d 1 x ⁺ d x^d 1 r ) ^X 1 ⁺

⁺ c 2 r d r ⁺ c 2 x d x - ^X 2 ⁽ b r^d 1 r ⁺ b x^d 1 x ) ;

B 1 = ^{- [} b r c 2 r ⁺ b x c 2 x ^- d r^d 1 r ^- d x^d 1 x ^{] X} 2 ⁺

^{+ [(} c 2 r ^{- X} 1 ^d 1 x ⁾⁽ c x ^- c 1 x ^{+ d} 1 x ) ^-

^{- (} c 2 x ^{+ X} 1 ^d 1 r ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ^)] - c 2 r ^- c 2 x ⁺

^{+ X} 1⁽ c 2 r^d 1 x ^- c 2 x^d 1 r ) ;

C 1 = ^- X 2 [ ⁽ c r ^- c 1 r ^- d r + d 1 r ) c 2 r +

+ c 2 x ⁽ c x - ^c 1 x - d x + ^d 1 x ^)] ;

A 2 = c 2 r d x - c 2 x d r - ^[ b r c 2 r + b x c 2 x + + ⁽ d r + X i b x )( c r - c i r - d r + d i r )] X i + ^{+ (} d x - X 1 b r ⁾⁽ c x - C 1 x - d x + d i x ) X 1 ;

B 2 = ^[( c 2 x ^{+ d} 1 r^X 1⁾⁽ c r - c 1 r - d r ^{+ d} 1 r ) -- X 1⁽ b r c 2 r + b x c 2 x ^{)] X} 1 ^{+ [} c 2 r ⁽ d x - ^d 1 x ) -- ^{( c} 2 r - ^d 1 x^X 1⁾⁽ c x - c 1 x - d x ^{+ d} 1 x ) -- c 2 x ⁽ d r - ^d 1 r ^{)] X} 1 ⁺ c 2 r ⁺ c 2 x ;

^C 2 = X 1⁽ C 2 r + c 2 x ) ^{X 2 (} c 2 r^d 1 x ^c 2 x^d 1 r ) .

ССЧ в виде П-образного соединения двухполюсников R ₁ , jX ₂ и jX ₃ (рис. 6, в ). При выборе комбинации ^ 1 , jX 2 в (16) надо положить X 1 = ^ ; X 2 = X 2 : A 1 = ^[( c r - c 1 r - d r ^{+ d} 1 r ^{) b} _r ^{+                             (21)}

⁺ b x ⁽ c x - ^c 1 x - d x ^{+ d} 1 x ^{)] X} 3 ⁺

^{+ X} 3^[( c r - ^c 1 r - d r ^{) d} 1 x ^{+ d} 1 r ^{( c} 1 x - c x ⁺ d x ) ⁺

⁺ b r c 2 x - b x c 2 r ^{] + c} 2 r^d 1 r ^{+ c} 2 x^d 1 x ^;

B 1 = c ² r ⁺ c 2 x ^{+ [(} c 1 r - c r - ^d 1 r ⁺ d r ^{) d}r ⁺

⁺ d x ^{( c} 1 x - c x - ^d 1 x ⁺ d x ) ⁺ b r c 2 r ⁺ b x c 2 x ^] X 3 ⁺

^{+ [(} c r - c 1 r - ² d r ) c 2 x ⁺ c 2 r ⁽ c 1 x - c x ^{+ 2} d x ^)] X 3 ;

• ^C 1 = - X 3⁽ c 2 r d r ⁺ c 2 x d x ) ;

A 2 = X 3^[ X 3⁽ b x d r - b r d x ) - b r c 2 r - b x c 2 x -

• - d r^d 1 r - ^dx^d 1 x ^] - c 2 r^d 1 x ⁺ c 2 x^d 1 r ;

B 2 = ^[( c 2 x - ^dr^X 3⁾⁽ c r - c 1 r - d r ^{+ d} 1 r ) -

• - X 3⁽ b r c 2 r ⁺ b x c 2 x ^)] X 3 ⁺

^{+ [ - (} c 2 r ^{+ d}x^X 3⁾⁽ c x ^- c 1 x ^- d x ^{+ d} 1 x ) ⁺

⁺ c 2 r ⁽ d x ^{- d} 1 x ) - c 2 x ⁽ d r ^{- d} 1 r ^)] X 3 ⁺

22 ⁺ c 2 r ⁺ c 2 x ;

^C 2 = X 3^[( c r ^- c 1 r ^- d r ^{+ d} 1 r ) c 2 x ^-

- c 2 r ⁽ c x ^{- c} 1 x ^- d x ^{+ d} 1 x ^{)] +} X 3⁽ c 2 r ⁺ c 2 x ) •

При выборе комбинации R ₁ , jX ₃ (рис. 6, в ) в (16) надо положить X 1 = R 1 ; X 2 = X 3 :

A 1 = ^[( c 1 r ^- c r ⁺ d r ) ^d 1 x ^{- d} 1 r ⁽ c 1 x ^- c x ⁺ d x ) ⁺

⁺ b r c 2 x ^- b x c 2 r ^{] X} 2 ^{+ (} b r^d 1 r ⁺ b x^d 1 x ) ^X 2 ⁺

^{+ (} c r ^- c 1 r ^- d r ^{+ d} 1 r ^)c2 r ⁺ c 2 x ⁽ c x ^- c 1 x ^- d x ^{+ d} 1 x ) ;

^C 1 = - ^X 2 ⁽ c 2 r d r ⁺ c 2 x d x ) ;

B 1 = ^X 2 ⁽ b r c 2 r ⁺ b x c 2 x ^- d r^d 1 r ^- d x^d 1 x ) ⁺

⁺ c ² r ⁺ c 2 x ^{- X} 2^[ c 2 x ⁽ c r ^{- c} 1 r ) - c 2 r ⁽ c x ^- c 1 x ^)];

A 2 = ⁽ c r ^- c 1 r ^- d r ^{+ d} 1 r ⁾⁽ c 2 x ^{- d}r^X 2 ) ^-- X 2⁽ b r c 2 r ⁺ b x c 2 x ) - ^X 2 ⁽ b r d x ^- b x d r ) ^{-- (} c 2 r ^{+ d}x^X 2⁾⁽ c x ^- c 1 x ^- d x ^{+ d} 1 x ) ;

B 2 = ^X 2^{[( c} 1 x ^- c x ^{+ 2} d x ^{- 2 d} 1 x ) c 2 r ⁺

⁺ c 2 x ⁽ c r ^- c 1 r ^{- 2} d r ^{+ 2 d} 1 r ^{)] -}

• ^- X 2⁽ b r c 2 r ⁺ b x c 2 x ⁺ d r^d 1 r ⁺ d x^d 1 x ) ⁺ c 2 r ⁺ c 2 x ;

^C 2 = ^X 2⁽ c 2 r ⁺ c 2 x ) - ^X 2 ⁽ c 2 r^d 1 x ^- c 2 x^d 1 r ) •

При выборе комбинации jX ₂ , jX ₃ (рис. 6, в ) в (16) надо положить X 1 = X 2 ; X 2 = X 3 :

A 1 = ⁽ b r c 2 r ⁺ b x c 2 x ^{+ d}r^d 1 r ^- d x^d 1 x ) ^R 1 -

• —    c 2 r d r — c 2 x d x ^{+ (} b r^d 1 r ⁺ b x^d 1 x ) R 1 ;

B 1 = ^R 2^[( c 1 r ^- c r ⁺ d r ) ^d 1 x ⁺ b r c 2 x ^- - b x c 2 r ^{- d} 1 r ⁽ c 1 x ^- c x ⁺ d x ^{)] -}

• ^{- R} 1^[( c r ^- c 1 r ) c 2 x ^- c 2 r ⁽ c x ^- c 1 x ^)] ;

^C 1 = ^R 1⁽ c 2 r ⁺ c 2 x ) ^{+ R} 1 ^[( c r ^- c 1 r ^- d r ^{+ d} 1 r ) c 2 r ⁺

⁺ c 2 x ⁽ c x — c 1 x — d x ^{+ d} 1 x ^)] ;

A 2 = ⁽ b r c 2 r ⁺ b x c 2 x ) ^R 1 - ⁽ c 2 r d r ⁺ c 2 x d x ) ^-

• ^{-    [(} d r ^- R 1 b r ⁾⁽ c r ^- c 1 r ^- d r + d 1 r ) +

• 3. Математическое и схемотехническое моделирование динамических звеньев

^{+ (} d x ^- R 1 b x ⁾⁽ c x ^- c 1 x ^- d x ^{+ d} 1 x ^)] R 1 ;

B 2 = ^[( c r ^- c 1 r ^- d r ^{) d} 1 x ^{+ d} 1 r ⁽ c 1 x ^- c x ⁺ d x ) ⁺

⁺ b r c 2 x ^- b x c 2 r ^{] R} 2 ^{+ R} 1^[( c 1 x ^- c x ^{+ 2} d x ) c 2 r ^- - c 2 x ⁽ c 1 r ^- c r ^{+ 2} d r ^)] ;

^C 2 = R 1 ⁽ c 2 r ⁺ c 2 x ) ^{+ R} 2 ⁽ c 2 r^d 1 r ⁺ c 2 x^d 1 x ) •

На рис. 7–10 для примера показаны результаты теоретических и экспериментальных исследований принципиальной и эквивалентной схем узкополосного усилителя, соответствующих структурной схеме рис. 1, а , в виде их частотных характеристик.

В качестве НЭ использован транзистор типа BFQ17PH, включенный по схеме с общей базой по высокой частоте (рис. 7, а ). Схема НЧ выполнена в виде параллельно соединенных НЭ и ЦОС с П-образным соединением трех элементов C 22 , C 23 , R 3 ₆ . Схема общей ЦОС построена в виде П-образного соединения трех элементов C 25 , C 26 , R 46 . Нагрузка выполнена на элементе R 47 . Сопротивление источника сигнала сформировано с помощью элемента R 30 . Схема ССЧ собрана в виде П-образного четы-

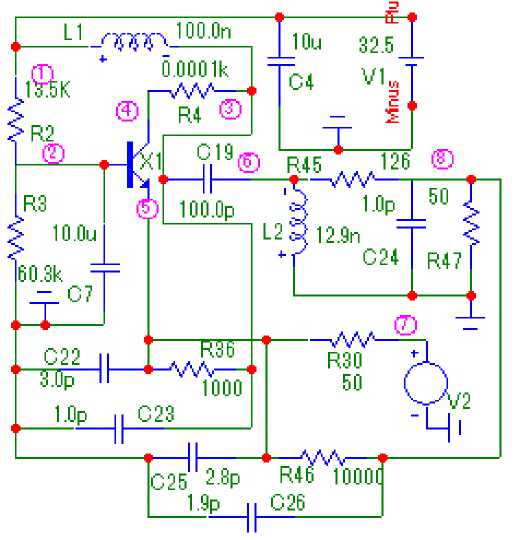
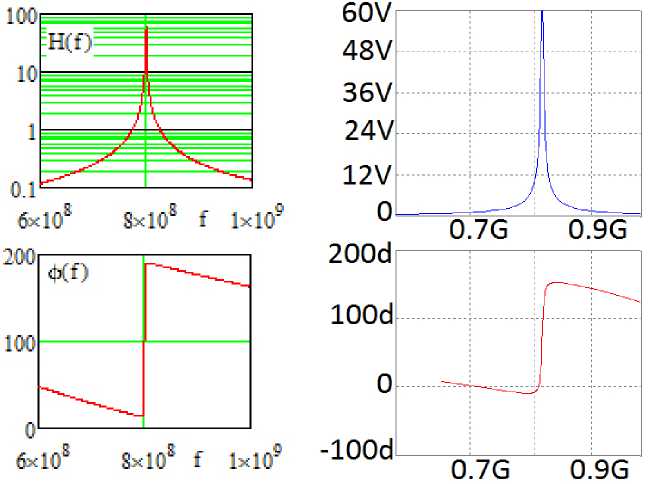
Рис. 7. Принципиальная схема узкополосного усилителя ( а ), соответствующая первой структурной схеме (рис. 1, а ). АЧХ- и ФЧХ-усилители, полученные в системе MicroCap ( б ) и в системе MathCad ( в ), показаны на рис. 8

Fig. 7. Schematic diagram of a narrow-band amplifier ( a ), corresponding to the first block diagram (Fig. 1, a ). The frequency response and phase response of the amplifier obtained in the MicroCap system ( b ) and in the MathCad system ( c ) are shown in Fig. 8

а                          б

Рис. 8. АЧХ- и ФЧХ-усилители (рис. 7), полученные в системе MicroCap ( а ) и в системе MathCad ( б )

Fig. 8. Frequency response and phase response of the amplifier (Fig. 7), obtained in the MicroCap system ( a ) and in the MathCad system ( b )

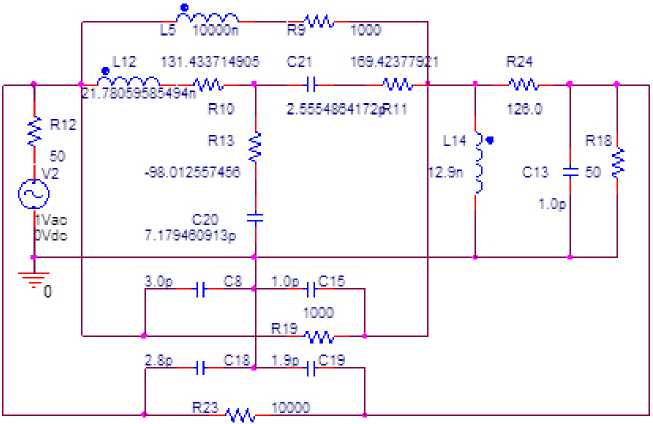
Рис. 9. Эквивалентная схема ( а ) узкополосного усилителя (рис. 7), соответствующего первой структурной схеме (рис. 1, а ). АЧХ и ФЧХ, полученные в системе OrCad, показаны на рис. 10 Fig. 9. Equivalent circuit ( a ) of a narrow-band amplifier (Fig. 7) corresponding to the first block diagram (Fig. 1, a ). The frequency response and phase response obtained in the OrCad system are shown in Fig. 10

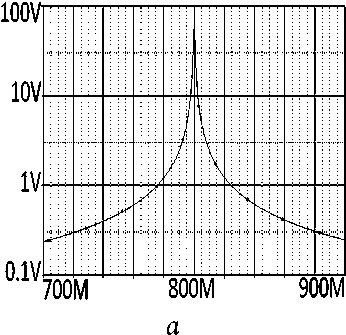
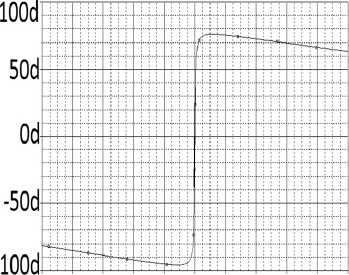
700М       800М       900М

б

Рис. 10. АЧХ ( а ) и ФЧХ ( б ) эквивалентной схемы (рис. 9), полученные в системе OrCad

Fig. 10. Frequency response (a) and phase response (b) of the equivalent circuit (Fig. 9), obtained in the OrCad system рехполюсника на элементах L2, C24, R45, параметры которых определялись по формулам (16), (19).

Эквивалентная схема транзистора выполнена в виде перекрытого Т-образного четырехполюсника на элементах L 12 , R 10 , C 20 , R 13 , R _n, C 21 , R 9 , L ₅ (рис. 9).

Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C 8 , C 15 , R 19 • Схема общей ЦОС построена в виде

П-образного соединения на основе трех элементов C 18 , C 19 , R 23 , а схема ССЧ - на основе П-образного соединения трех элементов L 14 , R 24 , C 13 '

Заключение

Анализ показывает, что экспериментальные (рис. 8, а) частотные характеристики (АЧХ и ФЧХ) принципиальной схемы узкополосного усилителя (рис. 7) удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 9) усилителя, полученные расчетным путем (рис. 8, б) и экспериментально (рис. 10). Резонансная частота эквивалентной схемы f ≈ 800 МГц (рис. 8, б и 10) незначительно отличается от резонансной частоты принципиальной схемы f ≈ 812 МГц (рис. 8, а). Произведение коэффициента усиления на полосу частот составляет примерно 200 МГц.

Таким образом, полученные математические модели ССЧ (10)–(21) могут быть использованы для технического проектирования различных динамических звеньев автоматических систем управления с обратной связью с заданными частотными характеристиками. Результаты можно также использовать для формирования заданных АЧХ- и ФЧХ-фильтров и квазилинейных склонов АЧХ высокочастотных частей (до фильтра нижних частот) демодуляторов сигналов с угловой модуляцией.