Параметрический синтез комплексных четырехполюсников для вариантов их включения между источником сигнала и нелинейной частью по критерию обеспечения заданных характеристик усилителей с общей обратной связью

В работе [1] предложен алгоритм параметрического синтеза согласующих комплексных четырехполюсников (КЧ), включенных в заданные структурные схемы усилителей, с учетом наличия нелинейной части (НЧ), состоящей из нелинейного элемента (НЭ) и охватывающей его параллельной или последовательной по току или напряжению обратной связи.

Цель данной работы состоит в расширении областей физической реализуемости заданных АЧХ- и ФЧХ-усилителей путем включения дополнительной цепи обратной связи ЦОС, охватывающей и НЧ, и КЧ.

Для достижения этой цели делается попытка определить минимальное количество двухполюсников и значения параметров КЧ, при которых обеспечиваются заданные частотные характеристики (зависимости модуля m и фазы ф передаточной функции H от частоты) усилителей с дополнительной обратной связью в одном из режимов работы нелинейного элемента (здесь и далее аргументы опущены):

H = m (cos ф + j sin ф ). (1)

Для составления исходных уравнений, удовлетворяющих (1), выделим в явном виде НЧ, которая может быть выполнена в виде НЭ с обратной связью или без нее, цепь прямой передачи (ЦПП) из КЧ и НЧ, а также общую ЦОС сопротивления источника сигнала z о = ? q + jx о и нагрузки ^z ^ = ^r ^ ⁺ К ⁽Р^ис. 1, 2).

1.    Алгоритм параметрического синтеза

Для отыскания передаточных функций исследуемых усилительных звеньев будем использовать известные правила применения матриц различных параметров для описания четырехполюсников и их соединений, а также условия нормировки общей матрицы передачи узла «КЧ–НЧ–ЦОС» [1; 2]. На основании этого запишем передаточную функцию для структуры с параллельной по напряжению ЦОС, показанной на рис. 1, а , в следующем виде:

z _H [ y Oc ( ab_v + bd_v ) + 1]

H =------- —--y---y ----------,     (2)

aA ₀ + bB 0 + cC 0 + dD 0 + ( ad - bc ) E 0 + H 0

где

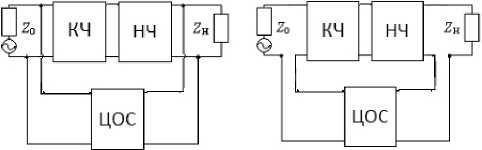
а                       б

Рис. 1. Структурные схемы усилительных звеньев с параллельной по напряжению ( а ), последовательной по току ( б ) общими цепями обратной связи и КЧ

Fig. 1. Structural diagrams of amplifying links with parallel voltage ( a ), series current ( b ) common feedback circuits and HF

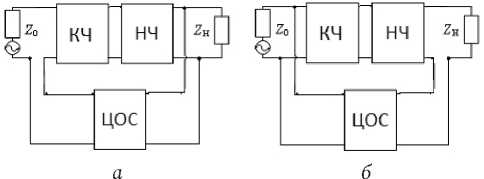
Рис. 2. Структурные схемы усилительных звеньев с последовательной по напряжению ( а ), параллельной по току ( б ) общими цепями обратной связи и КЧ

Fig. 2. Structural diagrams of amplifying links with serial voltage ( a ), parallel current ( b ) common feedback circuits and HF

A 0 = ^{[ y} oc y oc z 0 ^Z H + ^{( 1} + ^y Hz 0 ^{)( 1   y} 22 ^Z H ^{)] b} y +

^{+ a} y ^z u ^{( 1} + ^yH^z 0 ) ;   ^C 0 = ^z 0 ^{[ a} y ^z u + b y ^{( 1} - ^y 2 2 ^Z H ^)];

При использовании последовательной по току ЦОС (рис. 1, б ) передаточную функцию можно представить следующим образом:

B 0 = [ y &  2oi z 0 z_H + (1 + y& 0 )(1 - y °^_н )] d y +

^{+ c} y ^z n ^{( 1 + y} 11 ^z 0 ) ; ^D 0 = ^z 0 ^{[ c} y ^z n ⁺ d y ^{( 1 y} 22 ^z H ^)];

^H 0 = y¹ c z 0 ^z H ; ^E 0 = ^- y¹ c ^z 0 ^z H ^{( a} y ^d y ^{- b} y ^c y );

a y ’ b y , C y , d y — известные зависимости комплексных элементов классической матрицы передачи НЧ от частоты; y Ц , У 1c , У 2 c , У OC — известные зависимости элементов матрицы проводимостей ЦОС от частоты; a , b , c , d – искомые зависимости комплексных элементов классической матрицы передачи КЧ от частоты. Если положить y “С = 0, У “С = 0, У 2c = 0, У 2 2 = 0, то предлагаемый алгоритм синтеза оказывается справедливым и для усилителей без ЦОС и задача синтеза сводится к ранее решенной в [1] задаче. При синтезе КЧ без ЦОС и НЧ надо дополнительно принять a y = 1, b y = 0, C y = 0, d y = 1. Этот случай соответствует задаче синтеза неуправляемых динамических звеньев, согласующе-фильтрующих и корректирующих устройств. Если (1) означает обеспечение квазилинейного склона зависимости модуля передаточной функции от частоты, излагаемый материал применим и для синтеза высокочастотной части демодуляторов сигналов с угловой модуляцией.

Подставим (2) в (1). Получим комплексное урав- нение, решение которого приводит к взаимосвязи элементов классической матрицы передачи КЧ, оптимальной по критерию (1):

(C1 с + B) b + D1 d + C2 c + C z„ [ z21 (avc + cd) +1]

H =------------ ^{H 21 y} ----^y -----------------,        (4)

aA 0 + bB 0 + cC 0 + dD 0 + ( ad - bc ) E 0 + H 0

где

^A 0 = ^b y ^{+ a} y ^{( z} h  ^zOc ) ^{; B} 0 = ^d y ^{+ c} y ^{( z} h ^zOc ) ^;

^C 0 = ^{( z} 0 ^{+ z} 11 ^{)[ b} y ^{+ a} y ^{( z} H   ^z 22 ^{)] + a} y ^z 12 ^z 21 ;

D 0 = ( z 0 + z ic )[ d y + c y ( z_H - z 22)] + c y z ^z d;

^E 0 = ^z 1c ^{( a} y ^d y ^b y ^c y ); ^H 0 = ^z 1 2 ;

z “c , z “ 2 , z 2 c , z 2 c - известные зависимости элементов матрицы сопротивлений ЦОС от частоты.

Взаимосвязь между элементами классической матрицы передачи КЧ, оптимальную по критерию (1), можно также представить в форме (3), но при следующих уточнениях:

B = - B 0 M ; C = z_H - H 0 M ; C 1 = E 0 M ;         (5)

C 2 = a y z_Hz ic - C 0 M ; D = A 0 M ;

^D 1 = c y z_Hz2^c - ^D 0 ^M .

При использовании последовательной по напряжению ЦОС (рис. 2, а ):

z _H [ hic ( be + dd ) + 1]

H =----------- ^{H 21 y} ----^y -----------------,        (6)

aA ₀ + bB 0 + cC ₀ + dD 0 + ( ad - bc ) E 0 + H 0

где

^A 0 = ^a y ^z H ^{+ b} y ^{( 1 - h} 22 ^z H ) ;

^B 0 = ^c y ^z H ^{+ d} y ^{( 1 -} h oc z H );

^E 0 = ^{h1c z} н ^{( a} y ^d y ^{- b} y ^c y );

C 0 = ( z 0 + h ic )[ a y z_H + b y (1 - K ic z_H )] + b y h 1 ₂ ^ch 2 ¹ 1 ^cz_H ;

D 0 = ( z 0 + h H )[ c y z_H + d y (1 - K ic z_H )] + d y h 1 ₂ ^ch 2 c z_H ;

c

0    ^h 12 ^z н ;

h oc , h oC ’ h 2C ’ h "0C — известные зависимости элементов смешанной матрицы H ЦОС от частоты.

Коэффициенты для взаимосвязи (3) между элементами классической матрицы передачи ССЧ, оптимальной по критерию (1):

B = - B 0 M ; C = z_^ - H 0 M ; C _o = E 0 M ;         (7)

C o = W - C o M ; D = A 0 M ;

D 1 = d y z u h oc - D 0 ^M .

При использовании параллельной по току обратной связи (рис. 2, б ):

z ^ [ f oc ( a y a + C y b ) + 1]

H =------------------------------------------- ,        (8)

aAo + bBo + cCo + dDo + (ad - bc)Eo + Ho где

^C o = ^[ b y - a y ^{( f} 22 - ^z ^ ^{)] z} o ;

D o = ^[ d y - ^c y ^{( f} 22 ^{- z} ^ ^{)] z} o ;

E o = f oc ^z o ⁽ a y d y ^- b y ^C y );

A o = (1 + f oC z o )[ b y - a y ( f OC - z ^ )] + a y f o c f OC z o ;

B o = (1 + f OC z o )[ d y - C y ( f OC - z ^ )] + C y f c oC f o o l c Z o ;

• 2.    Результаты параметрического синтеза

Здесь в качестве примера приводятся некоторые из новых решений, полученных для типовых схем КЧ и структурной схемы, показанной на рис. 1, а . Число независимых решений равно количеству двухполюсников выбранных типовых схем КЧ. При соответствующем выборе характера свободных параметров результаты синтеза можно использовать при проектировании динамических звеньев радиоэлектронных систем автоматического управления [3–5]. Если в качестве КЧ используется последовательно включенный одиночный комплексный двухполюсник с сопротивлением z ₁ (рис. 3, а ), то зависимость этого сопротивления от частоты определяется следующим образом:

C - C + D - D₃

z o =  ----5------                             (^oo)

КЧ в виде параллельно включенного двухполюсника с сопротивлением z ₁ (рис. 3, б ):

z _o =

C ₂

C _o - C + D - D _o

oc

H o = J 12 ^z o ^;

f oC , f oc , f oc , f 22 — известные зависимости элементов смешанной матрицы F ЦОС от частоты.

Коэффициенты для взаимосвязи (3) для этого варианта:

B = z 2' - B o M ; C = z ^ - H o M ;              (9)

C ₁ = E _o M ; C ₂ = - C _o M ;

D = A o M - a f ; D o =- D o M .

Для отыскания выражений для определения параметров типовых схем КЧ необходимо взять известные элементы a , b , c , d [1; 2], выраженные через сопротивления двухполюсников, а также коэффициенты B , C , C o , C 2 , D , D o из (3), (5), (7), (9) с выбранным типом обратной связи и подставить их в (3). Решение сформированных таким образом комплексных уравнений определяется в виде зависимостей сопротивлений двухполюсников выбранных схем КЧ от частоты, оптимальных по критерию (1) на всех частотах. Эти зависимости в сплошной полосе частот (даже очень узкой) полностью реализовать невозможно. Однако возможно определение значений параметров квазиоптимальных двухполюсников, реальные частотные характеристики которых совпадают с оптимальными на заданном количестве частот и с заданными погрешностями в окрестностях этих частот (см. ниже).

КЧ в виде Г-образного соединения двухполюсников z o , z 2 (рис. 3, в ):

^C 2 ⁺ D o ^z 2 _____ C _o - C + D - D _o - Bz 2 ; z _o( C _o - C + D - D _o) - C ₂

D _o + Bz _o

КЧ в виде обратного Г-образного соединения двухполюсников z o , z 2 (рис. 4, а ):

_ C ₂ + z ₂ ( C - C _o - D + D _o)

'^o =         D - Bz 2

=      C 2 - Dz o

'² C _o - C + D - D _o - Bz_o"

КЧ в виде Т-образного соединения двухполюс-

ников z o , z 2 , z ₃ (рис. 4, 6 ):

z^. ( C - C - D + D. + Bz o) + C^ + z o D-. 2     1       1    3    2   31

D - B ( z 2 + z ₃)

z ₂ =

C ₂ - Dz _o + D _o z ₃ + Bz _o z 3

C _o - C + D - D _o - B ( z _o + z 3 );

z 2 ( C _o - C + D - D _o - Bz _o) + z _o D - C ₂ D _o + B ( z _o + z 2 )

КЧ в виде П-образного соединения двухполюсников z o , z 2 , z 3 (рис. 2, е ):

z o =

C ₂

- [ z ₃ ( C ₂ + z 2 D _o) + C ₂ z 2 ]

- z 2 D + z 3 ( C - C _o - D + D _o + Bz 2 ) ;

Рис. 3. Примеры синтезированных КЧ

Fig. 3. Examples of synthesized CNs

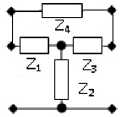
а

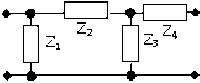
б

Рис. 5. Примеры синтезированных КЧ (продолжение)

Fig. 5. Examples of synthesized CNs (continuation)

а                б               в

Рис. 4. Примеры синтезированных КЧ (продолжение)

Fig. 4. Examples of synthesized CNs (continuation)

Рис. 6. Примеры синтезированных КЧ (продолжение)

Fig. 6. Examples of synthesized CNs (continuation)

_ C 2 z 1 + z 3 [ C 2 + z 1 ( C - C 1 - D + D 1 )]

z 4 _ { [ C 2 + z 3 ( C - C 1 + z 2 B )] z 1 +

+ ( C 2 - z 1 D )( z 2 + z 3 ) + z 3 D 1 ( z i + z 2 ) } /

/ - [( D 1 + z 1 B )( z 2 + z 3 ) + z i D i ].

КЧ в виде двух обратных Г-образных соединеНий двухполюсников z 1 , z 2 , z 3 , z 4 (рис. 3, в ): z i _ { ( C 2 + z 4 D 1 )( z 2 + z 3 ) + C 2 z 4 -

• - z2 D (z3 + z4) + z2 z4 (C - C1 + z 3 B)} /

  / { ^{( D - z} 4 ^{B )( z} 2 + ^z 3 ) + ^z 4 ^D } ^;

_    -[(C2 - z 1D)(z3 + z4)+ z3 z4(D1 + z 1B)].

• 2    " (C -C. -D + D3)z4 + C9 + (z. + zo)(z,B -D) ; 1       14   2   1   34

_ ( C ₂ - z 1 D )( z 2 + z 4 ) + z 2 z 4 ( C - C 1 - D + D 1 + z 1 B )

z3 _        -[(z4B - D)(z 1 + z2) + C2 + z4D1 ]’ z4 _{(z1 D - C2)(z2 + z3) + z2 z3d} /

/ { [( C - C 1 - D + D 1 + ( z i + z 3 ) B ] z 2 +

+ z 3 ( D 1 + z 1 B ) + C ₂ - z 1 D } .

КЧ в виде каскадно-соединенных Г-образного и П-образного соединений двухполюсников z 1 , z 2 , z ₃, z ₄, z ₅ (рис. 3, г ):

{[z 4(z 2 + z 3)+ z 2 z 3](C2 + z5 D1)+ z5 C2(z 2 + z 3)} z 1 _-------------------------------------------------------------;

^{[ C} 2 ^{- z} 2 ^{D + z} 5 ^{( D} 1 ⁺ Bz 2 ^)]( z 3 ^{+ z} 4 ) ^{+ Z} 01       (19)

^Z 01 ^{_ z} 5 ^{[ C} 2 ^{+ z} 3 ^{( C - C} 1 ^{+ z} 4 ^{B )] - D [ z} 3 ^{( z} 4 ^{+ z} 5 ) ^{+ z} 2 ^z 5 ^{] ;}

z 2 _

[( C - C 1 - D + D 1 + z 4 B ) z 5 + C 2 - z 4 D ] z 1 z 3 + Z ₀₂

^{- [( z} 3 + ^z 4 + ^z 5 ^{)( C} 2 ^{- z} 1 ^D ) + ^z 5 ^{( D} 1 + ^z 1 ^{B )( z} 3 + ^z 4 ^)]

^Z 02 ^{_ ( z} 1 ^{+ z} 3 ^{)[ C} 2 ^{( z} 4 ^{+ z} 5 ) ^{+ z} 4 ^z 5 ^D 1 ^] ;

_ ^{- {[ C} 2 ^{( z} 4 ^{+ z} 5 ) ^{+ z} 4 ^z 5 ^D 1 ^{)]( z} 1 ^{+ z} 2 ) ^{- Z} 04 ^} _

• ³    " [ C ₂ - z 1 D + z ₅ ( D 1 + z 1 B )]( z 2 + z 4 ) + Z ₀₃ ’

Z 03 _ C 2 ( z 1 + z 5 ) + z 1 z 5 ( C - C 1 - D + D 1 );

Z 04 _ z 1 z 2 [ D ( z 4 + z 5 ) - z 4 z 5 B )];

( C 2 z 1 D ) Z 5 ( z 2 + z 3 ) + C 2 [Z 3 ( z 1 + z 2 ) + z 1 z 5 ] + Z 05

z ^{4 _}     - {[C₂ - Dz 1 + Z₅ ( D 1 + z 1 B )]( z 2 + z 3 ) + Z ₀₆}     ’

а

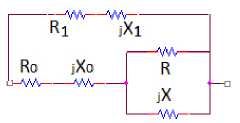
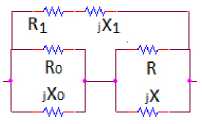
Рис. 7. Обобщенные квазиоптимальные комплексные двухполюсники

Fig. 7. Generalized quasi-optimal complex two-terminal networks

б

а

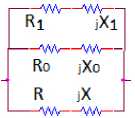
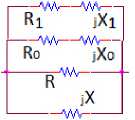
Рис. 8. Обобщенные квазиоптимальные комплексные двухполюсники (продолжение)

Fig. 8. Generalized quasi-optimal complex two-port networks (continued)

Z 05 — z 3 z 5 [ Z i ( C C i + ^^i ) + z 2 ( D i + z i B )] z i z 2 z 3 D ;

_— - {( C ₂ - z 1 D )[z₂ ( z 3 + z 4 ) + z 3 z 4 ] + C ₂ z 1 ( z 3 + z 4 )}, 5”      [ C - C 1 - D + D 1 + B ( z 2 + z 4 )] z 1 z 3 + Z 07     ’

Z 07 ^{— C} 2 ^{( z} i ^{+ z} 2 ^{+ z} з ) ⁺ D i ^{[( z} i ^{+ z} з ) ^z 4 ⁺

+ ( z 3 + z 4 ) z 2 ] - z _i z 2 ( D - Bz 4 ).

Аналогично для второго двухполюсника (рис. 4, б ):

r + jx —

RjX

R + jX

^R 0 j^X 0 1

^R 0 + j^X 0 J

( R i + jX i )

RjX + R^jX 0

R + jX R 0 + jX 0

+r2 + jX i

;

Частичную реализацию оптимальных частотных характеристик (10)–(19) будем проводить путем оптимизации параметров обобщенных ква-зиоптимальных реактивных двухполюсников,

X0 —

- B ₂ ± B 2 - 4 A ₂ C ₂

2 A ₁

;

включенных в состав квазиоптимальных ком-

плексных двухполюсников. Пусть требуется определить зависимости сопротивлений X ₀ и X реак-

X — - B2 ± Bb- - 4 A2 C2

2 A ₂

где

тивных двухполюсников от частоты, оптимальные по критерию обеспечения заданной зависимости комплексного сопротивления z — r + jx от частоты всех обобщенных двухполюсников, показанных на рис. 7.

Приравняем оптимальное комплексное сопро-

тивление z — r + jx , определенное в соответствии с (10)–(19), реальной зависимости сопротивления двухполюсника (рис. 4, а ) от частоты :

^R 0 ^{+ jX} 0 ⁺

r + jx —

RjX ) r + jx J

( R _i + jx _i)

^R 0 ^{+ jx} 0 ⁺ _R + jX ⁺ R i ^{+ jx} i

A i ^{— RR} 0 ^[ x ² + ^{( R} i ^- r ^{) 2 ]} + ^X 2 ^[ x ² + ^{( R} 0 ^- r ^{) 2 ] -}

• -    2 R ( rR 0 R 2 + xX _i R 0 ) - 2 xR 0 X _i R ² +

+ [ R ₂ R ² + R ( r2 + 2 R 0 R ₂ )](r ² + x ² ) -

• ^{-    R 2 {} r^R 2 ^{- X} 2 ^{( R} 0 ^- r ) ^{- R} 0 ^{[( R} i ^- r ^{) 2} + x ^{2 ]}};

B ₂ — 2 RR 0 [( r ² + x ² ) X _i - x ( R i + X 2 )];

C ₂ — {( r ² + x ² )[( R 2 + X 2 ) R + R ₂ R ² ] - rR ² ( R 2 + X 2 )} R 0 ;

A 2 — {[( R ₂ + R ) ² + X 2 ] R 0 + ( R ₂ + R ) R 0 }( r ² + x ² ) +

+ R 2 [ R 0 ( R ² - rR ₀) + R ( R 0 - 2 rR 0 )] -

После разделения (20) на действительную и мнимую части получим систему двух уравнений, решение которой имеет вид:

_ x ( R 2 + X 2 ) - X _i ( r ² + x ² ) + Q

X 0 ^—            о          О ;

⁽ R i ^{- r} ) ^{+ ( X} i ^{- x} )

X — QRI { ( R + R 0 )[( R _i - r ) ² + ( X _i - x ) ² ] + + R i ( r ² + x ²) - r ( R ² + X ² ) } ;

- 2 RR ₀ ( R ₂ r + X _i x )( R + R 0 ) +

+ R 0 X 2 [ R 0 ( R - r ) + R ( R - 2 r )];

B 2 — 2 R ₀ R ² [( r ² + x ² ) X _i - x ( r2 + X 2 )];

C ₂ — R ² { R ₂ R 0 ( r ² + x ² ) - ( R 2 + X 2 )[ rR 0 - R 0 ( r ² + x ² )]}.

Для третьего двухполюсника (рис. 8, а ):

r + jx

' ^{( R} 0 + j^X 0 ) ^R j_X R 0 + jX 0 + R¹

^{( R} 0 + j^X 0 ) ^R + j_X ^ R 0 + jX 0 + R ¹

^{- i}

( R ₂ + jX _i)

A ,

где

Q ^— ±^^{- {[(} R i ^{- r ) 2} + ^{( X} i ^{- x ) 2 ] R} 0 + + R i ⁽ r ² + x ² ) ^- r ⁽ R ² + ^{X 2 )}} Q 0 ;

Q 0 ^{— ( R + R} 0 ^{)[( R} i ^{- r ) 2 + ( X} i ^{- x ) 2 ] +} + R i ( r + x ) - r ( R i + X i ).

' ^{( R} 0 + j^X 0 ) ^R _jX R 0 + jX 0 + R¹

^{( R} 0 + j^X 0 ) ^R + j_X

( R 0 + jX 0 + R ¹

+ R i + jX i

Коэффициенты для (23):

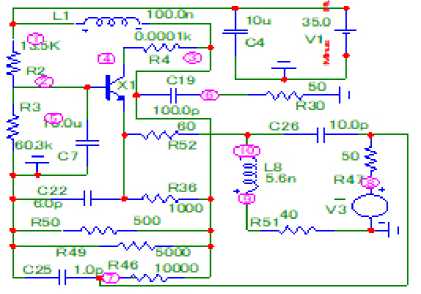
Рис. 9. Принципиальная схема узкополосного усилителя, соответствующая первой структурной схеме (рис. 1, а ). АЧХ- и

ФЧХ-усилители показаны на рис. 10

Fig. 9. Schematic diagram of a narrow-band amplifier corresponding to the first block diagram (Fig. 1, a ). The frequency response and phase response of the amplifier are shown in Fig. 10

а

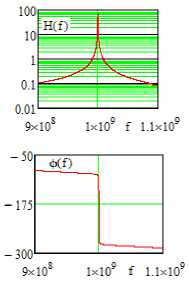
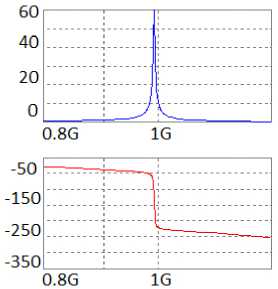
Рис. 10. АЧХ- и ФЧХ-усилители (рис. 9), полученные в системе MicroCap ( а ) и в системе MathCad ( б )

Fig. 10. Frequency response and phase response of the amplifier (Fig. 9), obtained in the MicroCap system ( a ) and in the MathCad system ( b )

б

A 1 = ( R ² R 1 + RR 2 + RX 2 )(r ² + x ² ) - rR ² ( R 2 + X 2 );

B 1 = 0;

C 1 = RR ₀ [( R + R ₀)( r ² + x ² ) - RR ₀ r ]( R 2 + X 2 ) +

+ R 1 R ² R 0 ( r ² + x ² );

C ₂ = R ² R ₀( R 2 + X 2 )( r ² + x ² );

A 2 = [( R 2 + X 2 )( R ₀ + R ) + R ² ( R ₀ + R 1 ) +

+ 2RR0R1 ](r2 + x2) + [R2 (R0 - r) - 2RR0r] x x (R2 + X2) - 2 R2 R0 (R1 r + X 1 x);

B 2 = 2 R 0 R ² [( r ² + x ² ) X 1 - x ( R 2 + X 2 )];

Для четвертого двухполюсника (рис. 8, б ):

r + jx

" ( R + jX^ )

R 0 + jX 0 + R + jX ¹ ' ¹

^{( R} 0 + jX 0 )^{( R} + jX )

+ R -i + 1A

R 0 + jX 0 + R + jX   ^{1    1}

Коэффициенты для (23):

A 1 = [( R 1 - r ) ² + ( X 1 - x ) ² ] R + R 1 ( r ² + x ² ) - r ( R 2 + X 2 );

B 1 = 2 R [( r ² + x ² ) X 1 - x ( R 2 + X 2 )];

C 1 = [( R + R ₀)( r ² + x ² ) - rR ₀ ( R ₀ + 2 R )]( R 2 + X 2 ) +

+ RR 2 [ R 1 ( R 1 - 2 r ) + X 1 ( X 1 - 2 x )] +

+ R 0 ( r ² + x ² )[ R 0 ( R + R 1 ) - 2 RR 1 ];

A 2 = ^{( r 2 + x 2 )( R} 0 ^{+ R} 1 ) ^{+ ( R} 2 ^{+ X} 2 ^{)( R} 0 ^{- r} ) ^-

• - 2 R 0 (R1 r + X 1 x);

3. Математическое и схемотехническое моделирование усилителей

B 2 = 2 R 0 [( r ² + x ² ) X 1 - x ( R 2 + X 2 )];

C 2 = ( r ² + x ² )[ R 0 ( R + R 1 ) ² + X 2 ( R + R ₀)] +

+ ( r ² + x ² )[ RR 1 ( R + R 1 ) - 2 R ² R 0 ( R 1 r + xX 1 )] +

+ [ R ² ( R ₀ - r ) - 2 rRR 0 ]( R 2 + X 2 ).

Таким образом, по крайней мере, для рассмотренных вариантов обобщенных квазиоптималь-ных двухполюсников (рис. 7, 8) задача обеспечения заданной зависимости комплексного сопротивления z = r + jx от частоты может быть сведена к задаче обеспечения необходимых (вспомогательных, дополнительных) зависимостей сопротивлений X ₀ и X реактивных двухполюсников от частоты, входящих в состав этих квазиоптимальных комплексных двухполюсников. Параметры реактивных двухполюсников, оптимальные по критерию обеспечения заданных частотных характеристик сопротивлений реактивных двухполюсников, определены в работе [1]. Количество частот, на которых может быть реализовано совпадение реальных и оптимальных характеристик комплексных двухполюсников, увеличивается до четырех. Полоса частот возрастает. Возможны и другие варианты квазиоптимальных комплексных двухполюсников, оптимизированных таким же образом. Для узкополосных усилителей использование этого этапа алгоритма параметрического синтеза не обязательно.

На рис. 9–12 в качестве примера показаны экспериментальные и теоретические характеристики эквивалентной и принципиальной схем узкополосного усилителя, соответствующих структурной схеме рис. 1, а . В качестве НЭ использован транзистор типа BFQ17PH, включенный по схеме с общей базой по высокой частоте (рис. 9). Схема НЧ выполнена в виде параллельно соединенных НЭ и

L5 1№3n

•10.029767

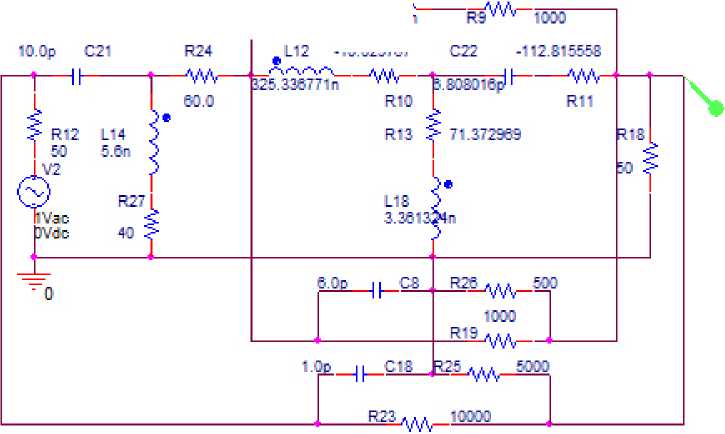
Рис. 11. Эквивалентная схема ( а ), узкополосного усилителя (рис. 9), соответствующего первой структурной схеме (рис. 1, а ). АЧХ- и

ФЧХ-усилители, полученные в системе OrCad, показаны на рис. 12

Fig. 11. Equivalent circuit ( a ) of a narrow-band amplifier (Fig. 9) corresponding to the first block diagram (Fig. 1, a ). The frequency response and phase response of the amplifier obtained in the OrCad system are shown in Fig. 12

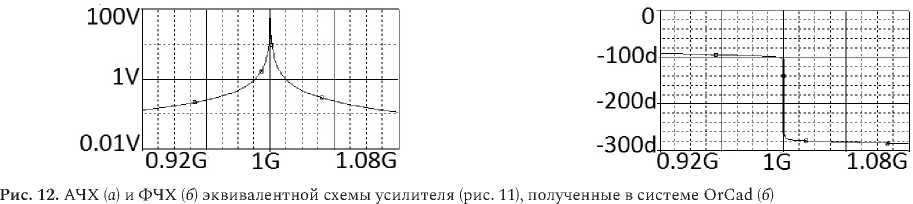
Fig. 12. Frequency response ( a ) and phase response ( b ) of the equivalent amplifier circuit (Fig. 11), obtained in the OrCad system ( b )

ЦОС с П-образным соединением трех элементов C 22 > R 36 > R 50 •

Схемаобщей ЦОС выполненаввиде П-образного соединения трех элементов C 25 , R 46 , R 49 •

Нагрузка и сопротивление источника сигнала выполнены на элементах R ₃₀ и R ₄₇ соответственно. Схема КЧ собрана в виде Т-образного четырехполюсника на элементах L 8 , C 26 , R 51 , R 52 , параметры которых определялись по формулам (14).

Эквивалентная схема НЭ выполнена в виде перекрытого Т-образного четырехполюсника на элементах L 12 , R ^, L 16 , R 13 , R 11 , C 22 , R 9 , L 5 (рис. 6, а ).

Схема НЧ выполнена в виде параллельно соединенных эквивалентной схемы НЭ и ЦОС с П-образным соединением трех элементов C 8 , R 19 , R 26 • Схема общей ЦОС выполнена в виде П-образного соединения трех элементов C 18 , R 23 , R 25 • Схема КЧ выполнена в виде Т-образного соединения четырех элементов L 14 , C 21 , R 24 , R 27 •

Заключение

Анализ показывает, что экспериментальные (рис. 10, а ) частотные характеристики принципиальной схемы узкополосного усилителя удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 11) усилителя, полученные расчетным путем (рис. 10, б ) и экспериментально (рис. 12). Резонансная частота эквивалентной схемы f ≈ 1000 МГц (рис. 10, б и 12) незначительно отличается от резонансной частоты принципиальной схемы f ≈ 992 МГц (рис. 10, а ). Произведение коэффициента усиления на полосу частот составляет примерно 200 МГц.

Таким образом, полученные математические модели КЧ (10)–(25) могут быть использованы для технического проектирования различных радиотехнических устройств с общей обратной связью, охватывающей нелинейную часть и согласующий КЧ, в интересах реализации заданных частотных характеристик.