Параметрический синтез радиоустройств с заданным количеством неодинаковых каскадов для вариантов включения реактивных четырехполюсников между нелинейной частью и нагрузкой

В работах [1–3] предложены алгоритмы параметрического синтеза согласующих четырехполюсников (СЧ), оптимальных по критерию обеспечения заданных характеристик усилителей, высокочастотных частей демодуляторов сигналов с угловой модуляцией, модуляторов и генераторов. При этом предполагалось, что нелинейная часть (НЧ) состоит из нелинейного элемента (НЭ) и охватывающей его цепи обратной связи (параллельной по напряжению, последовательной по току, последовательной по напряжению, параллельной по току). Исследовались структурные схемы, состоящие из одного каскада типа СЧ – НЧ и НЧ – СЧ.

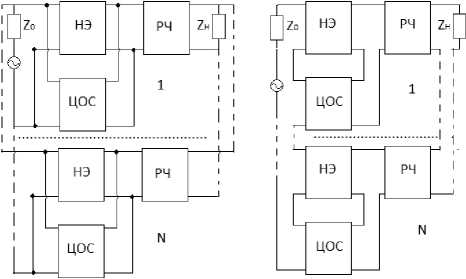
Цель данной работы состоит в увеличении произведения коэффициента усиления на рабочую полосу частот усилителей и демодуляторов путем включения произвольного количества неодинаковых каскадов типа «НЧ – реактивный четырехполюсник (РЧ)», включенных по той же схеме, что и НЭ и цепь обратной связи (ЦОС), между сопротивлениями источника сигнала z о = 1 q + jx о и нагрузки z _н = r _H + jx _н (рис. 1).

Для достижения этой цели делается попытка определить минимальное количество и значения параметров согласующих РЧ, при которых обеспечиваются заданные частотные характеристики

(зависимости модуля m и фазы ф передаточной функции H от частоты) усилителей и демодуляторов с произвольным количеством указанных каскадов в одном из режимов работы нелинейных элементов:

H = m (cos ф + j sin ф ), (1)

Согласующие РЧ n -го ( n = 1 , 2 .... N) каскада характеризуются искомыми зависимостями элементов a n , b n , c n , d n классической матрицы передачи от частоты.

Для составления исходных уравнений, удовлетворяющих (1), будем использовать известные правила применения матриц различных параметров для описания четырехполюсников и их соединений, а также условия нормировки общей матрицы передачи узла «НЧ – ЦОС – СЧ» [1; 4]. Рассмотрим вариант структурной схемы с параллельной по напряжению обратной связью (рис. 1, а ). Для этой схемы комплексные элементы классической матрицы передачи НЧ n -го каскада можно записать следующим образом:

a yn

'; b = А_ ; y 21 n     ^yn    y 21 n

cyn

-(У11 пУ22n - У12пУ21 n ). d   = У11 n y21n               yn   y21n

а                         б

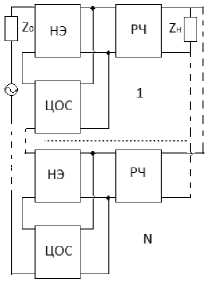
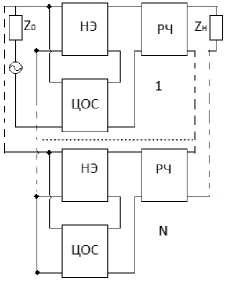
Рис. 1. Структурные схемы многокаскадных радиоустройств с параллельной по напряжению ( а ), последовательной по току ( б ), последовательной по напряжению ( в ), параллельной по току ( г ) цепями обратной связи, включенными между источником сигнала и РЧ

Fig. 1. Block diagrams of multistage radio devices with parallel in voltage ( a ), sequential in current ( b ), sequential in voltage ( c ), parallel in current ( d ) feedback circuits connected between the signal source and RF

в

г

íý oc íý oc íý где y 11 n = y 11 n + y 11 n; y 12n = y 12n + y 12n; y21 n = y21 n + + Уocn S У22n = У222n + У2cn - известные суммарные элементы матрицы проводимостей НЧ (НЭ и ЦОС).

Перемножим матрицы передачи НЧ и РЧ каждого каскада. Получим общие матрицы передачи и общие матрицы проводимостей отдельных ка-

C ym	_  —Ym   .		D n    oc В + Y 11 n
	1 B n	oc + Y 21	ym — + Y2 ° i c B n 21
где

m

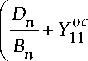
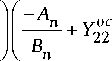
oc

скадов:

A Kn	A n C n	Bn D n	Y = ;      Kn =	Y 11 n Y 21 n	y19 12 n 22 n	,
где
An = a	a n yn	+ b yn jc n ; B n		= jb n	a yn + b yn d n
Cn = a	n c yn	+ d yn jc n ; D n		= jb n	c yn + d yn d n

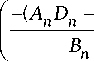
N

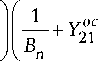
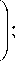
oc

Y 11        / .    Y 11m ;

m = 1, m ^ n

N

^Y0 =   / ^Y 12 m ;

m = 1, m ^ n

Y 11 n	= D n ; Bn	Y 12 n =	— ( A n D n — B n C n ) Bn
	1		— A
21 n	" Bn5	y99 = 22 n	n . Bn

Общая матрица проводимостей всех N каскадов

N

Y oc = / ^Y 21 m ;

m = 1, m ^ n

N

^Y0c =   /   ^Y22 m ;

m = 1, m * n

находится путем суммирования матриц проводимостей отдельных каскадов. Из сумм элементов матриц проводимостей выделим отдельно элементы матрицы проводимостей n -го каскадов и

Y °1 , ^Y°2 , Y 21 , Y 22 - известные зависимости суммарных элементов матрицы проводимостей всех каскадов (кроме n -го) от частоты.

Тогда передаточную функцию для структуры с параллельной по напряжению ЦОС, показанной на рис. 1, а , можно записать в следующем виде:

выразим их через элементы матрицы передачи. Остальные каскады можно рассматривать как цепи обратной связи. Следовательно, элементы общей матрицы передачи многокаскадной схемы можно записать в следующем виде:

H = { z ^ [ Y 21 ( d n b yn + ja yn b n ) + 1 ]}/

I ^{{ a}n A 0 ⁺ jb n B 0 ^{+ jc}n C 0 ⁺ d n D 0 ^{+                      (5)}

^{+ (} a n d n ⁺ b n c n ) E 0 ⁺ H 0 ^} , где

—

oc Y 22

—

An

Aym

B n

oc

Bym

B n

B n

oc 21

A 0 = z H ^[ c y z 0 ⁺ a yn ^{( 1 + Y}n^z 0^)];

B0 = [ Y12Y2O1Cz 0 zh + (1 + YUz 0)x x (1 — Y22zn)]ayn + cynz0(1 — Y2°2CzH);

C 0 = ^z h ^[ d yn z 0 ⁺ b yn ^{( 1 + Y} 1 ° 1 C z 0^)];

D 0 = ^{[ Y}12^Y21^z 0 ^z h ^{+ ( 1 + Y} n ^z 0 ) ^x

^х ( 1 ^Y2^Cz^ ^)] b yn + d yn z 0 ( 1 ^Y 22 ^z h ^);

E 0 = " Y l ^z 0 ^z^ ⁽ a yn d yn - b yn^Cyn );

H 0 = Y oc z 0 ^z^ ^;

Подставим (5) в (1). Получим комплексное уравнение, решение которого приводит к взаимосвязи элементов классической матрицы передачи РЧ n -го каскада, оптимальной по критерию (1):

a = (- Cl Cn + B) bn + D1 dn + C 2 Cn + C n          C dn + D где

B = j ( a y Y o 4 — B 0 M ) = b r + jb x ;

^C = z ^ — H 0 M = C r + jC x ;

C l = E 0 M = ^C 1 r + ^jC 1 x ^;

C 2 = ^{- jC} 0 M = ^C 2 r ^{+ jC} 2 x ^;

D = A 0 M = dr + jdx;

D 1 = b y^Y 2 ° i ^Cz _H D 0 M = d i r + jd i x ^;

M = m (cos ф + j sin ф ).

При использовании последовательной по току ЦОС (рис. 1, б ) передаточную функцию можно представить как:

H = { ^z^ ^{[ Z} 21⁽ a n^Cyn ^{+ jC}n^dyn ) ^{+ i ]}} /

/ ^{ a n^A 0 + jb n B 0 + ^jCn C 0 + d n^D0 +                     (7)

^{+ (} a n d n ^{+ b}n^Cn ) E 0 ⁺ H 0 ^} , где

A 0 = [( z 0 + Zh )( z ^ — Z 2 2 ) +

⁺ Z o^C Z 21 ^{] C}yn ⁺ a yn ⁽ z H - ^Z2 2^);

B 0 = a yn ^{+ C}yn ^{( z} 0 ^{+ Z}11 ^);    H 0 = ^Zo2 ^;

C 0 = [( z 0 + Zh )( z ^ - Z 2 2 ) +

⁺ Z o2^Z21 ^] d yn ⁺ b yn ^{( z} h - ^Z2 2^);

D 0 = b yn ⁺ d yn ^{( z} 0 ^{+ Z}11 ^);

E 0 = - ^Z21 ⁽ a yn d yn - b yn^Cyn ^);

NN

oc Z11 = Z Z11 m; oc Z12 = Z Z12 m; oc Z21 m=1, m ^ n N = Z  Z 21 m; m=1, m ^ n oc Z22 m=1, m ^ n N = Z  Z 22 m; m=1, m ^ n oc    oc    oc    oc Z11, Z12 , Z21, Z22 марных элементов – известные зависимости матрицы сопротивлений сум-всех каскадов (кроме n-го) от частоты.

Взаимосвязь между элементами классической матрицы передачи ССЧ, оптимальную по крите- рию (1), можно также представить в форме (6), но при других коэффициентах:

B = - jB 0 M = b r + jb x ;

^C = z ^ — H 0 ^M = C r + jC x ;

^C 1 = E 0 ^M = ^C 1 r ^{+ jC} 1 x ^;

_oc                                                   (8)

^C 2 = ^jdyn^z н ^Z2i - ^jC 0 ^M = ^C 2 r ^{+ jC} 2 x ^;

D = A 0 ^{M - C}y ^z h ^Z 21 = d r ^{+ jd}x ^;

D 1 = ^- D 0 M = d 1 _r + ^j d 1 x .

При использовании последовательной по напряжению ЦОС (рис. 1, в ):

H = { z ^ [ H 2 o 1 ^C (jb n C yn + d n d yn ) + 1 ]}/

/ ^{ a n A 0 ⁺ jb n B 0 ^{+ jC}n^C 0 ^{+ d}n D 0 ^{+                      (9)}

+ (andn + bC) E 0 + H 0 }, где

A 0 = ^z^ ^[ a yn ^{+ C}yn ^{( z} 0 ^{+ H}11 ^)];

B 0 = ^{( 1} - ^H 2 2 ^z^ ) a yn ⁺

+ c yn [ ^{( 1} - ^H^ ) ⁽ z 0 + ^HOC ) + H o 2 ^C H 2 ^o 1 ^C z_H ^] ;

^H 0 = ^HO2 ^z ^ ^{; C} 0 = ^z^ ^[ b yn ⁺ d yn ^{( z} 0 ^{+ H}1‘C ^)];

D 0 = ^{( 1} — ^H02C z ^ )by n +

+ d yn [( 1 - H °^ )( z 0 + H OC ) + H O 2 ^C H OC z h ];

oc

0    21 ^ yn yn yn yn ^;

	N		N
oc H 11	= Z H 11 m ;	oc H 12	= Z   H 12 m ;
	m = 1, m ^ n		m = 1, m ^ n
	N		N
oc H 21	= Z H 21 m ;	oc H 22	= Z H 22 m .
	m = 1, m ^ n		m = 1, m ^ n

H oC , H OC , H 21 , H 22 — известные зависимости суммарных элементов смешанной матрицы H всех каскадов (кроме n -го) от частоты.

Коэффициенты для взаимосвязи (6) между элементами классической матрицы передачи ССЧ, оптимальной по критерию (1):

B = j ⁽ C yn H 2C z H - B 0 ^M ) = b r + jb x ;

^C = z ^ - ^H 0 ^M = C r + jC x ;

^C 1 = E 0 ^M = ^C 1 r ^{+ jC} 1 x ^;                               (10)

^C 2 = ^{- jC} 0 ^M = ^C 2 r ^{+ jC} 2 x ^;

D = A 0 M = dr + jdx;

D 1 = ^dyn^HOC z H D 0 ^M = ^d 1 r ^{+ jd}1 x .

При использовании параллельной по току обратной связи (рис. 1, г ):

H = { ^z^ ^[ F olc ⁽ a n a yn + jb yn c n ) + ^{l ]}} /

/{ a n A 0 + jb n B 0 + jC n C 0 + ^dn D 0 +                   (11)

+ (andn + bncn) E 0 + H 0 }, где

A 0 = [ FnFOlz 0 + (l + Folz 0)x x (z^ -F22 )]ayn + cynz0(z^ -F22 );

B 0 = a yn ^{( l +} F l o l c z 0^{)] + z} 0 c yn ^;

H 0 = F O Z 0 ;

C 0 = [ F№ 0 + ( z ^ - F 2 ^o 2 c ) X

x ( l + F l o l c z 0)] b yn + d yn z 0( Z H -	F O );
D 0 = d yn z 0 + b yn ( l + F l o l c z 0);
oc 0    21 0 yn yn yn yn	;
N	N
oc                        oc F ll =   2^   F ll m ;    F l2 =	2 F l2 m ;
m = l, m ^ n	m = l, m ^ n
N	N
oc                        oc F 2l =   2   F 2l m ;    F 22 =	2   F 22 m ;
m = l, m ^ n	m = l, m ^ n

F l >  F l2 >  F 2l >  F 22 — известные зависимости суммарных элементов смешанной матрицы F всех каскадов (кроме n -го) от частоты.

Коэффициенты для взаимосвязи (6) для этого варианта:

B = - jB 0 M = b r + jb x ;

C = z ^ - H 0 M = C r + jC x ;

C l = E 0 M = c 1 r ⁺ jc 1 x ^;

_oc                                          (12)

C 2 = j ⁽ b yn^Z H F 2l - C 0 M ) = c 2 r ^{+ jc} 2 x ^;

D = A 0 M - ^ayn^Z _H ^F 2 ° l ^C = d r + jd x ^;

D l =- D 0 M = d l r + jd l x .

Для отыскания выражений для определения параметров типовых схем РЧ n-го каскада необходимо взять известные формулы для элементов an, bn, cn, dn [l; 4], выраженные через сопротивления или проводимости двухполюсников, а также коэффициенты B, C, Cl, C2, D, Dl с выбранным типом обратной связи и подставить их в (6). Затем полученное комплексное уравнение надо разделить на действительную и мнимую части и решить сформированную таким образом систему двух алгебраических действительных уравнений относительно сопротивлений или проводимостей двух двухполюсников выбранной схемы РЧ из M двухполюсников. В результате получаются огра- ничения в виде зависимостей сопротивлений двух реактивных двухполюсников от частоты, оптимальные по критерию (1). Задача реализации этих частотных характеристик в ограниченной полосе частот решена в работе [1]. Параметры остальных M-2 двухполюсников РЧ и ЦОС n-го каскада, свободных от указанных ограничений, а также параметры двухполюсников РЧ и ЦОС всех остальных каскадов выбираются из условия обеспечения других критериев, например из условия обеспечения заданной формы полосы рабочих частот [1]. Для этого могут быть использованы известные численные методы оптимизации [5]. При этом время оптимизации сокращается в сотни раз по сравнению с временем оптимизации с помощью только численных методов. Это связано с тем, что при использовании получаемых таким образом ограничений на каждом шаге оптимизации, включая первый, на заданном количестве частот обеспечивается совпадение реальных значений передаточной функции с заданными (1).

2. Результаты параметрического синтеза

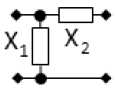
Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем РЧ, при использовании параллельной по напряжению обратной связи (рис. 1, а ). Если в качестве РЧ используется Г-образное соединение двух двухполюсников (рис. 2, а ), то зависимости их сопротивлений X ₁₂ от частоты (ограничения) определяются следующим образом:

X =        c 2 r X 2 d l r _;

^O c r ~ c l r ^- d r ⁺ d l r ⁺ X 2 b r

_ - B 2 ± V B 2² - 4 A 2 C 2

X 9 =--------------------,

²          2 A ₂

где

A 2 = b x d lr ^- b r d lx ^;

B 2 = ⁽ c x ^- c l x ^- d x ^)dlr ⁺

⁺ d l x ⁽ c l r ^- c r ⁺ d r ) ⁺ b r c 2 x ^- b x c 2 r ^;

C 2 = ⁽ c l x ^- c x ⁺ d x ^- d l x^)c 2 r ⁺

⁺ c 2 x ⁽ c r ^- c l r ^- d r ⁺ d l r ^).

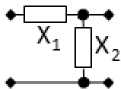
Обратное Г-образное соединение двухполюсников X ₁₂ (рис. 2, б ):

X _l =

⁽ c r ^- c l r ^- d r ⁺ d l r ) X 2 ^- c 2 r

d r - X 2 b r

б

в

г

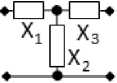
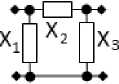
Рис. 2. Примеры синтезированных РЧ для устройств с заданным количеством каскадов типа НЧ-РЧ

Fig. 2. Examples of synthesized RF for devices with a given number of stages of the LF-RF type

^- В 2 ± BB ^{2 -} 4 A 2 С 2

X-) —---------------------

²          2 A ₂

где

A 2 ^{— (} c r - ^c 1 r - d r + ^d 1 r ) b x -

- b r ⁽ c x ^- C 1 x ^- d x + d i x ^);

^B 2 ^{— ( c} 1 r - c r - d i r ) d x ⁺

⁺ d r ⁽ c x - ^c 1 x ⁺ d i x ) ⁺ b r c 2 x - b x c 2 r ^;

^C 2 ^{— c} 2 r d x - ^c 2 x d r •

Т-образное соединение двухполюсников X ₁₂₃ (рис. 2, в ):

^{( c} 1 r - c r ⁺ d r - ^d 1 r - ^X 3 b r ) ^X 2 ^{+ c} 2 r - ^X 3 ^d 1 r ^{( X} 2 ^{+ X} 3 ) b r - d r

- B 2 ± B 2 - 4 A 2 C 2

2 A ₂          ’

где

A 2 ^{— (} c r ^- c 1 r ^- d r ^{+ d} 1 r ) b x ^-

^- b r ⁽ c x ^- c 1 x ^- d x ^{+ d} 1 x ^);

^B 2 ^{— (} X 3 b x ^- d x ⁾⁽ c r ^- c 1 r ) ⁺

⁺ b r ⁽ c 2 x ^{- 2 X} 3 ^d 1 x ) ^- b x ⁽ c 2 r ^{- 2 X} 3 ^d 1 r ) ^{+ + (} c x ^- c 1 x ⁾⁽ d r ^{- X} 3 b r ) ⁺ d r^d1 x ^- d x^d1 r ^;

^C 2 ^{— (} b x^d 1 r ^- b r^d1 x ) ^X 3 ^{+ (} b r c 2 x ^- b x c 2 r ^{+ +} d r^d 1 x ^{- d}x^d1 r ) ^X 3 ⁺ c 2 r d x ^- c 2 x d r ^;

⁽ c 1 r ^- c r ⁺ d r ^{- d} 1 r ^{- X} 3 b r ) X 2 ⁺ c 2 r ^{- X} 3 ^d 1 r ^{( X} 2 ^{+ X} 3 ) b r ^- d r

- ^B 3 ± V ^B 3 - ⁴ A 3 ^C 3

2 A 3        ’ где

A 3 ^— b x^d 1 r   b r^d1 x ^;

B3 = [ X2(cr  c 1 r + 2 d1 r) c2 r] bx br[c2x   X2(cx   c 1 x + 2d1 x)] + drd1 x   dxd1 r;

^C 3 = ⁽ b r d x ^- b x d r ) ^X 2 ^{+ X} 2^[ b r c 2 x ^- b x c 2 r ^-

• ^{- (} d x ^{- X} 2 b x ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ) ^{+ (} d r ^{- X} 2 b r ) ^X

^{X (} c x ^- c 1 x ^{+ d} 1 x ^{)] +} c 2 r d x ^- c 2 x d r ;

X =   ⁽ d r ^{- X} 3 b r ) ^X 1 ⁺ c 2 r ^{- X} 3 ^d 1 r   .

• ²    c r ^- c 1 _r ^- d r ^{+ d} 1 _r ^{+ ( X} 1 ^{+ X} 3 ) b r

_ - ^B 3 ± V ^B 3² - ⁴ A 3 ^C 3

^{X 3} =       2 A 3

где

A 3 = b x^d 1 r ^- b r^d 1 x ^;

^B 3 = ^{( d} 1 r ^{+ X} 1 b r ⁾⁽ c x ^- c 1 x ) ^{- (} c r ^- c 1 r ) ^X

• ^{X ( d} 1 x + X 1 b x ) ⁺ b r c 2 x ^- b x c 2 r ⁺ d r^d 1 x ^- d x^d 1 r ;

C 3 = ( b r d x - b x d r ) X 12 + X 1 ( b r c 2 x - b x c 2 r ) +

⁺ c 2 x d r ^- c 2 r d x ^{+ (} c 2 x ^{+ X} 1 d x ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ) ^-

• ^{- (} c 2 r ^{+ X} 1 d r ⁾⁽ c x ^- c 1 x ^{+ d} 1 x )•

П-образное соединение двухполюсников X _{12 3} (рис. 2, г ):

X = ^d 1 r^X 2 ^X 3 ^- c 2 r ^{( X} 2 ^{+ X} 3 ) ,

• ^{1    (} c 1 r ^- c r ⁺ d r ^{- d} 1 r ^{- X} 2 b r ) ^X 3 ⁺ c 2 r ^{+ X} 2 d r

_ - B 2 ± B^B 22 - 4 A 2 C 2

X Q —                      ,

• ²          2 A ₂

где

A 2 ^{— (} b x^d 1 r ^- b r^d1 x ) ^X 3 ^{+ (} b r c 2 x ^- b x c 2 r ⁺

⁺ d r^d 1 x ^{- d}x^d 1 r ) ^X 3 ⁺ c 2 r d x ^- c 2 x d r ^;

^B 2 ^{— [} c 2 r d x ^- c 2 x d r ^{- (} c 2 x ^{- X} 3 ^d 1 x ^{)( c} 1 r ^- c r ⁺ d r ) ⁺

^{+ (} c 2 r ^{- X} 3 ^d 1 r ⁾⁽ c 1 x ^- c x ⁺ d x ^{)] X} 3 ⁺

• 3    r 2 x     x 2 r ^;

^C 2 ^{— [} c 2 x ⁽ c r ^- c 1 r ^- d r ^{+ d} 1 r ) ^-

• ^-    c 2 r ⁽ c 1 x ^- c x ^- d x ^{+ d} 1 x ^{)] X} 3^;

X _— ^d 1 r^X 2 ^X 3 ^- c 2 r ^{( X} 2 ^{+ X} 3 ) , ^{1  (} d r ^- c r ^{- d} 1 r ⁺ E 0 M ^{- X} 2 b r ) ^X 3 ⁺ c 2 r ^{+ X} 2 d r

_ - ^B 3 ± V ^B 3² - ⁴ A 3 ^C 3

X 3 —       2A3       , где

A 3 ^{— (} b x^d 1 r ^- b r^d 1 x ) ^X 2 ⁺ c 2 x ^{( d} 1 r ^{+ X} 2 b r ) ^-

• ^-    c 2 r ^{( d} 1 x ^{+ X} 2 b x ) ^{- (} c 2 x ^{- X} 2 ^d 1 x ⁾⁽ c 1 r ^- c r ⁺ d r ) ⁺

^{+ (} c 2 r ^{- X} 2 ^d 1 r ⁾⁽ c 1 x ^- c x ⁺ d x ^);

^B 3 ^{— (} b r c 2 x ^- b x c 2 r ^{+ d}r^d1 x ^- d x^d1 r ) ^X 2 ⁺

^{+ [} c 2 r ⁽ c 1 x ^- c x ^{+ 2} d x ) ^- c 2 x ⁽ c 1 r ^- c r ^{+ 2} d r ^{)] X} 2^;

^C 3 ^{— X} 2 ⁽ c 2 r d x ^- c 2 x d r ^);

а

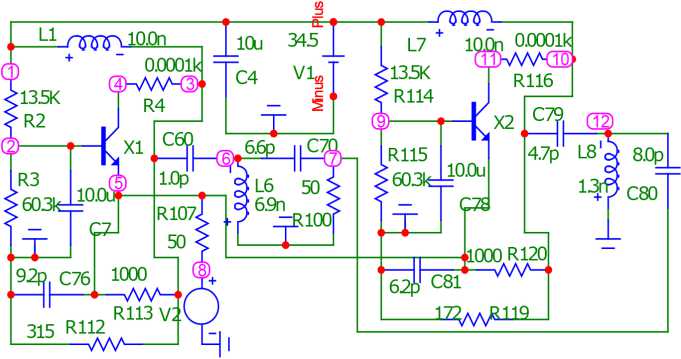
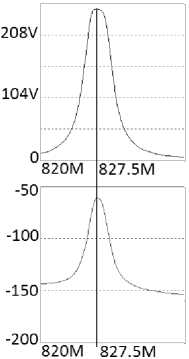
Рис. 3. Принципиальная схема двухкаскадного широкополосного усилителя ( а ), соответствующая первой структурной схеме (рис. 1, а ), АЧХ и ФЧХ усилителя, полученные в системе MicroCap ( б )

Fig. 3. Schematic diagram of a two-stage broadband amplifier ( a ) corresponding to the first structural diagram (Fig. 1, a ), frequency response and phase response of the amplifier obtained in the MicroCap system ( b )

б

X 2 =

⁽ c r - ^c 1 r - d r + ^d 1 r ) X 1 X 3 - ^c 2 r ⁽ X 1 + X 3 ) ^c 2 r - X 3 ^d 1 r ⁺ X 1 ( d r - X 3 b r )

X 3 =

- B 3 ±

V B 32 - ⁴ A 3 C 3

2 A ₃

где

A 3 = [ b x ( c 2 r - X 1 ^d 1 r ) - b r ( c 2 x - X 1 ^d 1 x ) +

+ (d1 x + X1 bx)(C1 r - Cr + dr) - (d1 r + X1 br) X x (c 1 x - cx + dx)]X1 + c2rd1 x - c2xd1 r;

B 3 = ⁽ b x c 2 r - b r c 2 x - ^dr^d 1 x ^{+ d}x^d 1 r ) X 1 ⁺

⁺ X 1 ^[( c r ^- c 1 r )( c 2 x + X 1 d x ) ^-

• ^{- (}cx - c 1 x⁾⁽c2r⁺X1 dr^)];

3. Математическое и схемотехническое моделирование усилителей

C 3 = X 1⁽ c 2 x d r ^- c 2 r d x )•

На рис. 3, 4 для примера показаны принципиальная и эквивалентная схемы двухкаскадного широкополосного усилителя, соответствующие структурной схеме рис. 1, а , и их теоретические и экспериментальные характеристики. В качестве НЭ использован транзистор типа BFQ17PH , включенный по схеме с общей базой по высокой частоте (рис. 3, а ).

Схемы НЧ-усилителя выполнены в виде параллельно соединенных НЭ и ЦОС в виде П-образного соединения трех элементов C76, R112, R113 и C81, R119, R120 • Нагрузка выполнена на элементе RWo • Сопротивление источника сигнала выполнена на элементе R^ • Схемы РЧ собраны в виде Т-образного четырехполюсника на элементах L6, C60, C70 и L8, C79, C80, значения параметров двух из которых определялись по формулам (15). Остальные параметры РЧ и ЦОС определялись численно. Эквивалентные схемы нелинейного элемента выполнены в виде перекрытых Т-образного звеньев на элементах R27, L22, R3, и R30, L26, R33, C35, R31,

C 30 , ^R 28 , L 23 , R 9 , L 19

L 27 , R 29 , L 25 (рис. 4, а). Значения параметров эквивалентной схемы нелинейного элемента выбраны из условия совпадения значений выходного сопротивления НЧ [1] с аналогичными значениями при использовании реального транзистора.

Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C 8 , R 19 , R 26 и C 36 , R 35 , R ₃₆ . Схема РЧ реализована на основе Т-образного соединения трех элементов L 28 , C 33 , C 34 • Физический смысл и назначение остальных элементов принципиальной и эквивалентной схем очевидны.

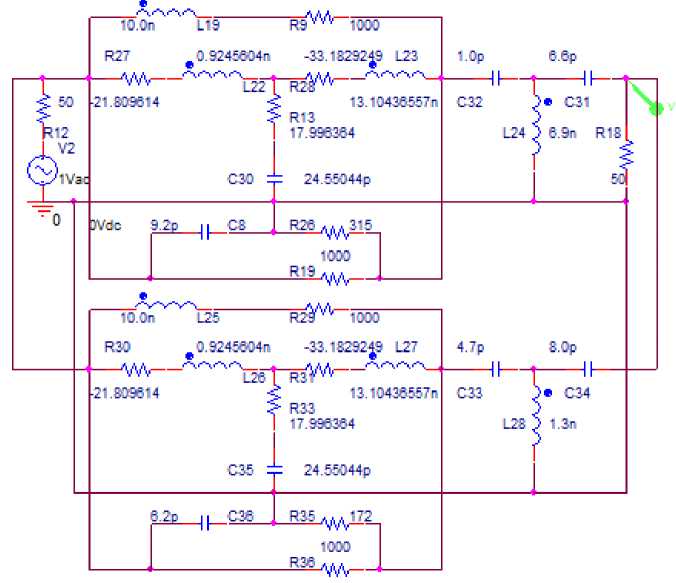
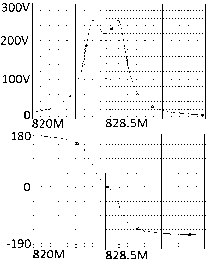
Анализ характеристик, представленных на рис. 3, 4, показывает, что экспериментальные (рис. 3, б ) частотные характеристики принципиальной схемы широкополосного двухкаскадного усилителя (рис. 3, а ) удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 4, а ) усилителя, полученные расчетным путем (рис. 4, в ) и экспериментально (рис. 3, б , 4, б ). Некоторые отличия экспериментальных (рис. 3, б ) и расчетных характеристик могут быть объяснены имеющимися погрешностями используемой эквивалентной схемы нелинейного элемента. Средняя частота рабочей полосы частот эквивалентной схемы f « 828 , 5 МГц (рис. 4, б и в ) незначительно

0.9245Ю4П

18292^3 127

■E^V'/V

6.2d i । C36

6.6p

• C31

L24 J 6.9n R18

JVdc

R26

3'5

нгУ^-- ззз

R30

■21.809614

R33 17.996364

TSTr^--

<        13.10436557П

C35

1V«

C33

• C34

-,3г

10.3n

RS^-1000

-33.18292^9 123

д^ул—■^.■^.■^.■^_

13.10436557ц

R13

17.996364

C33

24.55344p

R27

'--Wv-

■2- i:?:4

б

а

в

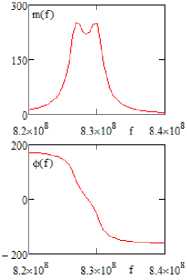
Рис. 4. Эквивалентная схема ( а ) широкополосного усилителя (рис. 3, а ), соответствующего первой структурной схеме (рис. 1, а ), и ее АЧХ и ФЧХ, полученные в системе OrCad ( б ) и в системе MathCad ( в )

Fig. 4. Equivalent circuit ( a ) of a broadband amplifier (Fig. 3, a ) corresponding to the first structural diagram (Fig. 1, a ), and its frequency response and phase response obtained in the OrCad system ( b ) and in the MathCad system ( с )

отличается от средней частоты принципиальной схемы f ≈ 827 , 5 МГц (рис. 3, б ). Произведение коэффициента усиления на полосу частот АЧХ составляет примерно 700 МГц. Это примерно в 8–9 раз больше площади усиления однокаскадного усилителя.

Таким образом, полученные математические модели РЧ-типа (13)–(16) могут быть использованы для технического проектирования различных многокаскадных усилителей и демодуляторов в интересах реализации заданных частотных характеристик.