Параметрический синтез радиоустройств с заданным количеством одинаковых каскадов для вариантов включения реактивных четырехполюсников между источником сигнала и нелинейной частью

В работах [1–3] предложены алгоритмы параметрического синтеза согласующих четырехполюсников по критерию обеспечения заданных частотных характеристик усилителей, генераторов, модуляторов и демодуляторов. Предполагалось, что нелинейная часть (НЧ) состоит из трехполюсного нелинейного элемента (НЭ) и охватывающей его цепи обратной связи (параллельной или последовательной по току или напряжению).

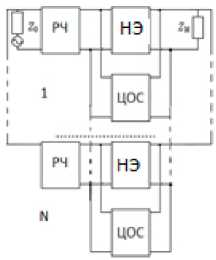
Цель данной работы состоит в расширении функциональных возможностей таких радиоустройств путем включения произвольного количества N дополнительных одинаковых каскадов типа «реактивный четырехполюсник (РЧ) – НЧ»; между источником сигнала с сопротивлением z о = Г д + jx о и нагрузкой z _н = r _H + jx _н (рис. 1). Каскады между собой соединены с использованием того вида обратной связи, по которому соединены НЭ и цепь обратной связи (ЦОС).

Для достижения этой цели делается попытка определения минимального количества двухполюсников РЧ и значения их параметров, при которых обеспечиваются заданные частотные характеристики (зависимости модуля m и фазы ф

передаточной функции H от частоты) перечисленных радиоустройств в одном из режимов работы НЭ (аргументы опущены):

H = m (cos ф + j sin ф ).

Согласующий РЧ характеризуется искомыми элементами классической матрицы передачи a , jb , jc , d .

1. Алгоритм параметрического синтеза

Для отыскания передаточных функций исследуемых радиоустройств можно использовать известные правила применения матриц различных параметров для описания четырехполюсников и их соединений, а также условия нормировки общей матрицы передачи узла «РЧ – НЧ» [1; 4]. Рассмотрим вариант структурной схемы с параллельной по напряжению обратной связью (рис. 1, а ). Для этой схемы комплексные элементы классической матрицы передачи НЧ одного каскада можно записать следующим образом:

ay

cy

- y ²² ; b_y = -; y 21      ^yy 21

⁽ y 11 y 22    y 12 y 21 ) _;

y ₂₁

d = y 11 , ^yy ₂₁

б

в

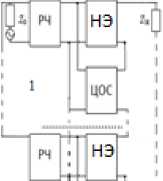
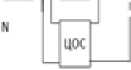
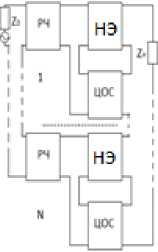
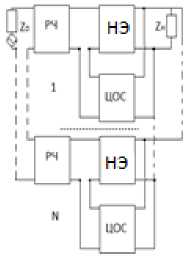
Рис. 1. Структурные схемы многокаскадных радиоустройств с параллельной по напряжению ( а ), последовательной по току ( б ), последовательной по напряжению ( в ), параллельной по току ( г ) цепями обратной связи, включенными между РЧ и нагрузкой Fig. 1. Block diagrams of multistage radio devices with parallel in voltage ( a ), sequential in current ( b ), sequential in voltage ( c ), parallel in current ( d ) feedback circuits connected between the RF and the load

íý oc           íý oc           íý oc где y 11 - y 11 + y 11; y 12 - y 12 + y 12; y21 - y21 + y21;

y 22 - У 22 + У 22 — известные суммарные элементы матрицы проводимостей НЧ (НЭ и ЦОС).

Перемножим матрицы передачи РЧ и НЧ одного каскада. Получим общую матрицу передачи и общую матрицу проводимостей каскада:

C ₌ _ j ⁽ b y + Na y z_H ) d y ^{+ Nc}y z H

D -----------

= ^cr ^{+ jc}x ;

zí

m [cos( ф ) + j sin( ф )] z 0 ( d_y + Nc_yz_H )

= d r ^{+ jd}x •

A K -	A 1 C 1	B 1 D 1	;    y k -		Y 11   Y 12 Y 21   Y 22	,                              (3)
где
A 1 - aa y +		jbcy ;		B 1	= aby + jbdy ;
C 1 - c y d +		a yjc ;		D 1 -	b y jc + d y d ;
Y 11 -	D 1 - B 1 ’	Y 12 -		- ( A 1 D 1 - B 1 C 1 B 1		);
	1			- A 1 • B 1
Y 21 -	B 1-	Y 22 -

Аналогичные операции проводим для остальных вариантов. При использовании последовательной по току ЦОС (рис. 1, б ) элементы классической матрицы передачи НЧ одного каскада удобно выразить через элементы матрицы сопротивлений:

a	- z 11 ;	b v -	( z 11 z 22 z 12 z 21 ) ;
y	z 21	y	z 21	(6)
c	- 1	d v -	- z 22 ,
y	z 21	y	z 21

где z ₂₂

z ₁₁ íý ^- z 22

íý

- z 11

oc

⁺ z 22

oc

-11 ;

z ₁₂

íý z ₁₂

oc

' 12 ;

z ₂₁

íý z ₂₁

+ z

oc

– известные суммарные элементы

Общая матрица проводимостей всех N каскадов находится путем суммирования матриц проводимостей отдельных каскадов. Поэтому общая передаточная функция всего устройства может быть записана следующим образом:

H - Nz_H I {( jb + Ndz 0 )( d_y + Nc_yz_H ) +

+ ( a + Njcz 0 )( b y + Na_yz_B )}.

Подставим (4) в (1). Получим комплексное уравнение, решение которого приводит к взаимосвязи элементов классической матрицы передачи РЧ, оптимальной по критерию (1):

d - Aa + Bb + Cc + D ,                            (5)

где

^{- (} b y + Na y z_H ) _

^Nz 0 ^{( d} y ⁺ Nc y z H ) ^ar+)x^{X ;}

B = NL . b r + jb x ^;

матрицы сопротивлений НЧ (НЭ и ЦОС).

Перемножим матрицы передачи РЧ и НЧ одного каскада. Получим общую матрицу передачи (3) и общую матрицу сопротивлений каскада:

Zê

Z 11

Z 21

Z 12

Z 22

где

_ A 1_       _-( A 1 D 1 - B 1 C 1)_

^Z11 ^- C ’ Z 12 ^- C       >

Z 21 ^-_r^;

C ₁

- D

1Z22 - r

C ₁

Общая матрица сопротивлений всех N каска-

дов находится путем суммирования матриц сопротивлений отдельных каскадов. Поэтому общая передаточная функция всего устройства может быть записана следующим образом:

H - Nz_H I {( Nb_y + a_y z_H )( Na + jcz 0 ) + + ( Nd_y + c_yz_H )( Njb + dz 0 )}•

Подставим (8) в (1). Получим комплексное урав-

нение, решение которого приводит к взаимосвязи (5) элементов классической матрицы передачи РЧ, оптимальной по критерию (1), но с другими коэффициентами:

^{N ( Nb}y ^{+ a}y^Z ^ )

A = -                = a , + ja_v ;

z о ( Nd y + C y z ^ )     r x*’

B = — — b r + jb x ;

z 0   ^rx

C = - ^{j ( Nb}y ⁺ a y ^ ) ^Ndy ^{+ c}y^z ^

= c r ^{+ jc}x ;

N ( by + NayZ ^ ) A — -                — a , + jaY ; z о ( d y + Nc y z ^ )     r ' x’
B—-^ — b r + jb x ; z 0   rx j ( by + NayZ ^ )       _	(13)
C        ,                   c 1 )CV ; d y + Ncyz ^ Nz D —----------------- ^ ---------------— d r + jd x • m [cos( 9 ) + j sin( ф )] z 0 ( dy + Ncyz^ )

При использовании параллельной по току обратной связи (рис. 1, г ) элементы классической матрицы передачи НЧ одного каскада проще определить через элементы смешанной матрицы f :

D —

Nz í m [cos(ф) + j sin(ф)] z 0 (Ndy + cyz^)

= d r ^{+ jd}x •

При использовании последовательной по напряжению ЦОС (рис. 1, в ) элементы классической матрицы передачи НЧ одного каскада целесообразно определить через элементы смешанной матрицы h :

ay f ^; f ₂₁

by

Z f22 ; f ₂₁

. _ ^f 11 .    3 _ ⁽ f 11 f 22 f 12 f 21 )

cy — f ; dy —         f f21                   f21

a = ^{( h} 11 h 22 ^h 12 h 21 ) . b _— ^h 11 .

^y            h 2i         ^; y h 2i ^;

C —- h ! • d — _!_ ^y h 2i      ^y h 2i ,

íý oc íý oc íý oc где J11 — J11 + J11 ; J12 — J12 + f 12 ; f21 — f21 + f21 ; f22 — J12 + f'00 — известные суммарные элементы смешанной матрицы f НЧ (НЭ и ЦОС).

Перемножим матрицы передачи РЧ и НЧ одного каскада. Получим общую матрицу передачи (3) и общую смешанную матрицу F_k каскада:

íý oc           íý oc где hii — h11 + h11; h12 — h12 + h12 ;

h 21 — h 2i + h oc ;

h 22 — h o2 + h o2 — известные суммарные элементы

смешанной матрицы h НЧ (НЭ и ЦОС).

Перемножим матрицы передачи РЧ и НЧ одного каскада. Получим общую матрицу передачи (3) и общую смешанную матрицу H_k каскада:

Hê

H ₁₁

H ₂₁

H ₁₂

H ₂₂

Fê

F ₁₁

F ₂₁

F ₁₂

F ₂₂

где

F11 —

F 21 ^—

C 1 _;

A ₁

A ₁

F 12 ^—

( A 1 D 1 - B 1 C 1 )

-B-

F ^{22 —} A 1

A ₁

где

_ B 1 ,       _ ⁽ A D i - B i C i) .

H ¹¹ = D 1 ^; H ¹² = D 1     ^;

- C

H i— —; H₂ —— •

21 D ₁ 22    D ₁

Общая смешанная матрица всех N каскадов на- ходится путем суммирования смешанных матриц Hk отдельных каскадов. Поэтому общая передаточная функция всего устройства может быть записана следующим образом:

H — Nz_H / {( d_y + Nc_yz_H )( dz 0 + Njb ) + + ( jcz 0 + Na )( b y + Na_yz_^ )}•

Подставим (12) в (1). Получим комплексное уравнение, решение которого приводит к взаимосвязи (5) элементов классической матрицы передачи РЧ, оптимальной по критерию (1), но с уточненными коэффициентами:

Общая смешанная матрица всех N каскадов на- ходится путем суммирования смешанных матриц Fk отдельных каскадов. Поэтому общая передаточная функция всего устройства может быть записана следующим образом:

H — Nz_H / {( Nd y + c_yz_H )( jb + Ndz 0 ) + + ( a + Njcz 0 )( Nb y + a_yz_^ )}•

Подставим (16) в (1). Получим комплексное уравнение, решение которого приводит к взаимосвязи (5) элементов классической матрицы передачи РЧ, оптимальной по критерию (1), но с новыми коэффициентами:

B—— — br+jbx; zí j ( by + NdyZ 0 ) ay + Ncyz 0

^— c r ^{+ jc}x ;

_   ^{N (} b y + Nd y z 0 )

^{D    Z} ^ ⁽ a y + Nc y z 0 )

^_ d r + jd x ;

dz ₀ + jb dz_Q + Njb C0~r_a ^ jcz 0 + Na •

---------------------------------_ er + jex m [cos(q) + j sin(Q)]( ay + Ncyz 0)

Анализ выражения для передаточной функции (4) показывает, что частотные характеристики исследуемых радиоустройств из N одинаковых каскадов типа РЧ-НЧ (рис. 1, а) идентичны АЧХ и ФЧХ радиоустройств из одного каскада, но с со- противлениями источника сигнала и нагрузки, умноженными на N (рис. 2, а). В общем случае частотные характеристики исследуемых радиоустройств из N2 групп одинаковых каскадов по N1 не обязательно одинаковых каскадов типа РЧ – НЧ в каждой группе идентичны АЧХ и ФЧХ радиоустройств из одной группы N1 не обязательно одинаковых каскадов типа НЧ – РЧ, но с сопротивлениями источника сигнала и нагрузки, умноженными на N2.

Анализ выражения для передаточной функции (8) показывает, что частотные характеристики исследуемых радиоустройств (рис. 1, б) из N одинаковых каскадов типа РЧ – РЧ идентичны АЧХ и ФЧХ радиоустройств из одного каскада, но с со- противлениями источника сигнала и нагрузки, разделенными на N (рис. 2, б). В общем случае частотные характеристики исследуемых радиоустройств из N2 групп каскадов по N1 не обязательно одинаковых каскадов типа РЧ – НЧ в каждой группе идентичны АЧХ и ФЧХ радиоустройств из одной группы N1 не обязательно одинаковых каскадов типа РЧ – НЧ, но с сопротивлениями источника сигнала и нагрузки, разделенными на N2.

Анализ выражения для передаточной функции (12) показывает, что частотные характеристики исследуемых радиоустройств (рис. 1, в ) из N одинаковых каскадов типа РЧ – НЧ подобны АЧХ и ФЧХ радиоустройств из одного каскада, но с сопротивлением нагрузки, умноженным на N , и измененным выходным сопротивлением РЧ (рис. 2, в ):

dz 0 + jb dz 0 + Njb jcz 0 + a jcz 0 + Na

.

Правая часть выражения (18) означает, что сопротивление источника сигнала разделяется на N (рис. 2, в ). Модуль передаточной функции умножается на N . Правая часть выражения (19) означает, что сопротивление источника сигнала разделяется на N 2 . Модуль передаточной функции умножается на N 2 . Полосы частот полностью совпадают.

Анализ выражения для передаточной функции (16) показывает, что частотные характеристики исследуемых радиоустройств (рис. 1, г ) из N одинаковых каскадов типа РЧ – НЧ подобны АЧХ и ФЧХ радиоустройств из одного каскада, но с сопротивлением нагрузки, разделенным на N , и измененным выходным сопротивлением РЧ (рис. 2, г ):

dz 0 + jb dz 0 + jb IN jcz 0 + a jcz 0 + a IN

.

В общем случае частотные характеристики исследуемых радиоустройств из N ₂ групп каскадов по N ₁ не обязательно одинаковых каскадов типа РЧ – НЧ в каждой группе подобны АЧХ и ФЧХ радиоустройств из одной группы N ₁ не обязательно одинаковых каскадов типа РЧ – НЧ, но с сопротивлением нагрузки, разделенным на N 2 , и измененным выходным сопротивлением РЧ:

^dy^z 0 ⁺ b y    ^dy^z 0 ⁺ b y ^{1 N} 2

c y z 0 ⁺ a y    ^cy^z 0 ⁺ a y ^1N 2 .

Правая часть выражения (20) означает, что со- противление источника сигнала умножается на N (рис. 2, г). Модуль передаточной функции разделяется на N. Правая часть выражения (21) означает, что сопротивление источника сигнала умножается на N2 . Модуль передаточной функции разделяется на N2 . Полосы частот полностью совпадают. Такие схемы будем называть эквивалентными. Они могут значительно упростить решение многих задач радиоэлектроники, например задач обеспечения распространения сигнала только в одном направлении (от входа к выходу) и независимости предыдущего каскада от присоединения последующего. Эти свойства необходимы для динамических звеньев при построении радиоустройств автоматического регулирования.

Для отыскания выражений для определения параметров типовых схем РЧ необходимо взять известные формулы для элементов a , b , c , d [1; 4], выраженные через сопротивления или проводимости двухполюсников, а также коэффициенты A , B , C , D для (5) с выбранным типом обратной связи.

а                            б                            в                            г

Рис. 2. Структурные схемы однокаскадных радиоустройств с параллельной по напряжению ( а ), последовательной по току ( б ), последовательной по напряжению ( в ) и параллельной по току ( г ) цепями обратной связи, эквивалентные со схемами, показанными на рис. 1, а , б , в , г

Fig. 2. Block diagrams of single-stage radio devices with parallel in voltage ( a ), sequential in current ( b ), sequential in voltage ( c ) and parallel in current ( d ) feedback circuits, equivalent to the circuits shown in Fig. 1, a , b , c , d

а

б

в

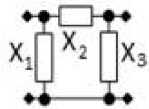
г

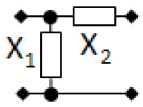
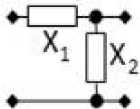
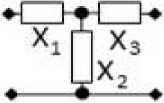
Рис. 3. Примеры синтезированных реактивных СЧ для многокаскадных устройств

Fig. 3. Examples of synthesized reactive midrange for multistage devices

Затем надо разделить полученное комплексное уравнение на действительную и мнимую части и решить сформированную таким образом систему двух действительных алгебраических уравнений относительно сопротивлений или проводимостей двух двухполюсников выбранной схемы РЧ из N двухполюсников. В результате получаются ограничения в виде зависимостей сопротивлений двух реактивных двухполюсников от частоты, оптимальных по критерию (1). Задача реализации этих частотных характеристик в ограниченной полосе частот решена в работе [1]. Параметры остальных N - 2 двухполюсников, свободных от указанных ограничений, выбираются из условия обеспечения других критериев, например из условия обеспечения заданной полосы рабочих частот [1].

где Л₉ — h ; B₉ — a_x + d - bc + bc ; C₉ — c - ac + x       x x rx xr       x rx

+ a c + cd - cd . xr r x x r

Обратное Г-образное соединение двух сопро тивлений jX 1 2 (рис. 3, б):

_y _ ^cr - ^X 2^{( a}r ⁺ d r - ¹⁾. ;

ar + X 2 br v _ - B2 ± BB-4 4 Л2 C2

X o — -------------------,

²           2 A ₂

где Л9 — bY - arbY + ah + bd - bd ; B9 — aY + ad - x rx xr r x x r        x rx

- ad - bc + bc ; C₉ — ac - ac . x r rx xr       xr rx

Т-образное соединение двухполюсников jX 1 2 3

(рис. 3, в ):

X 1 —

X 3 + c r - X 2 ( a r + d r + X 3 b r - 1) ^ar ^{+ ( X} 2 ^{+ X} 3 ^{) b}r

2. Результаты параметрического синтеза РЧ при использовании каскадов типа РЧ – НЧ

- B ₉ ±

X 2 —    ²

У B 2 - 4 Л 2 ^C 2

2 A ₂

где

Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем РЧ и структурной схемы, показанной на рис. 1, а . Если в качестве РЧ используется Г-образное соединение двух сопротивлений jX ₁₂ (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом:

Л₂ — b (1 - a - d ) + b ( a + d ); x r r rx x

^B2 ^{— a}x ^{+ a}r^dx - ^ax^dr - b r c x ⁺

+ bc + X. (2 b + bd - bd ); xr         x   r x   x r

C ^— b X 2 ^{+ ( a -} he ⁺ b c ) ^X ₃ ^{- a} c ^{+ ac} ;

x     x  rx  xr      rx xr

X 1 —

X 3 + c r - X 2 ( a r + d r + X 3 b r - 1)

^ar ^{+ ( X} 2 ^{+ X} 3 ^{) b}r

;

X 1 =

X 2 ⁺ c r _;

a r + d r + X 2 b r - 1 ’

X ₂ =

— B ₂ ±

B 2 - 4 A 2 C ₂

2 A ₂

X 3 —

- B ₃ ± B^B-

’3² -

2 A ₃

4 A ₃ C ₃

)

где

^Л 3 ^{— b}x ^;

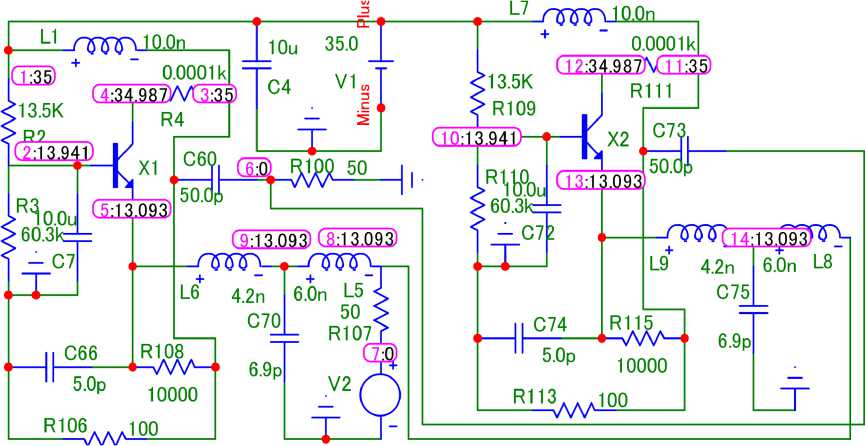
а

Рис. 4. Принципиальная схема двухкаскадного узкополосного усилителя ( а ), соответствующая структурной схеме (рис. 1, а ), и его частотные характеристики ( б ), полученные в системе MicroCap

Fig. 4. Schematic diagram of a two-stage narrow-band amplifier ( a ), corresponding to the structural diagram (Fig. 1, a ), and its frequency characteristics ( b ), obtained in the MicroCap system

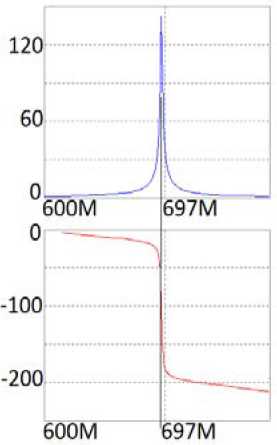
б

B o = a - b c + b c + X ₂ (2 b + b d - b d ); x rx xr        x r x x r

C = [ b_x (1 - a - d _r) + b ( a + d_x )] X 2 + x r r rx x

^{+ ( a}x ^{+ a}r^dx ^{- a}x^dr ^- b r c x ⁺ b x c r ) ^X 2 ^- a r c x ^{+ a}x c r ;

X = c r + X 3 ^- X 1^{( a}r + X 3 b r ) _;

( X i + X з ) b_r + d r + e r - 1

• - B o ±,/ B 2 - 4 A,Co

X 3    3    33

= ,

• ³           2 A ₃

где

A 3 = ^bx ^;

B o = a + d - X ₁ ( b_rd„ - bd ) - b_rc_x + b_xc_r ; x x r x x r rx xr

Co = ( a b - a b ) X ₁² + ( ad - ad - a_x - xrrx   xrrxx

• - bc + b c ) X + c (1 - a + d ) + c ( a + d ). rx xr x r r r x x

П-образное соединение двухполюсников jX 1 2 3 (рис. 3, г ):

X1 ________X3(X2 + cr) + X2 cr_______. X2 ar - cr + X3 (ar + dr + X2 br -1) (25) X2 - B2 ± BB- - 4 A2 C2 =        2 A2        , где

A n = b X n + ( a - b c + b c ) Xo - a c + a c ; x      x rx xr      rx xr

C ₂ = X 2 [ c r ( a_x + d x ) + c x (1 - a r - d r )];

• ^B 2 = ^X 3^{( a}x ^{+ d}x ^{- b}r^cx ⁺ bxcr ) ⁺ x x rx xr

^{+ X} 3^{( 2 a}x^cr ^{- 2 a}r^cx ^{+ c}r^dx ^{- c}x^dr ^);

_X = ^X 3^{( X} 2 ⁺ c r ) ^{+ X} 2 c r _;

X 2 a r - c r + X 3 ( a r + d r + X 2 b r - 1)

• - B o ±_Л/ B 2 - 4 A o C o

X3    333

= где

A3 = bxX2 + (c + X2)(a + d ) + x    rxx

+ c (1 - a - d ) - X ( b c - b c ) x r r       rx xr

B3 = Xo (2 a c - 2 a c + c d - c d ) + xr rx r x x r

• + X n ( a - b c + b c ); x rx xr

• ^C 3 = ^X 2 ^{( a}x^{c - a}r^cx ^); xr rx

_X = ( X 1 + X 3 ) c_r + X 1 X 3 (1 - a_r - d_r ) , ²”     X 1 a_r - c_r + X 3 ( X 1 b r - 1)    ;

X ₃ =

- B 3 ± 7 ^B 3 ² - 4 A 3 C 3

2 A ₃

где

A 3 = [ b_x (1 - a_r - d ) + b ( a_x + d_x )] X. ² + x r r rx x

• + ( bc - bc - a_x - d_x ) X + c_x ; xr rx x x x

Bo = X12 (a + a d - a d - x rx xr

• - b c + b c ) - X ₁ ( c d - c d ); rx xr       r x x r

• ^C 3 = ^X 2 ^{( a}x^{c - a}r^cx ). xr rx

• 3. Математическое и схемотехническое моделирование усилителей с одинаковыми каскадами типа РЧ – НЧ

Здесь для примера показаны принципиальная и эквивалентная схемы однокаскадного и двухкаскадного узкополосных усилителей (рис. 4–9), соответствующих исследуемым структурным схемам с параллельной по напряжению связью, пока-

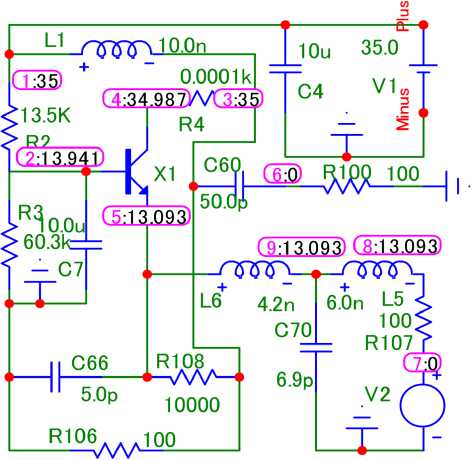
а

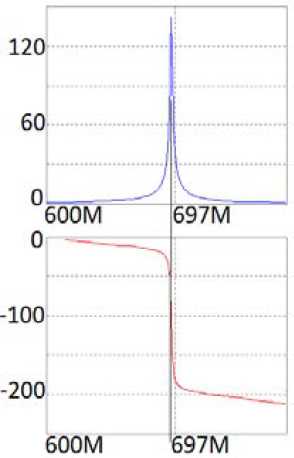
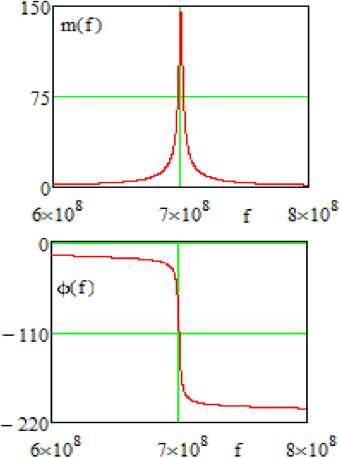
Рис. 5. Принципиальная схема однокаскадного узкополосного усилителя ( а ), соответствующая структурной схеме (рис. 2, а ), его частотные характеристики ( б ), полученные в системе MicroCap, и частотные характеристики его эквивалентной схемы, полученные в системе MathCad ( в )

Fig. 5. Schematic diagram of a single-stage narrow-band amplifier ( a ) corresponding to the structural diagram (Fig. 2, a ), its frequency characteristics ( b ) obtained in the MicroCap system, and the frequency characteristics of its equivalent circuit obtained in the MathCad system ( c )

б

1-™

-106.737064

а

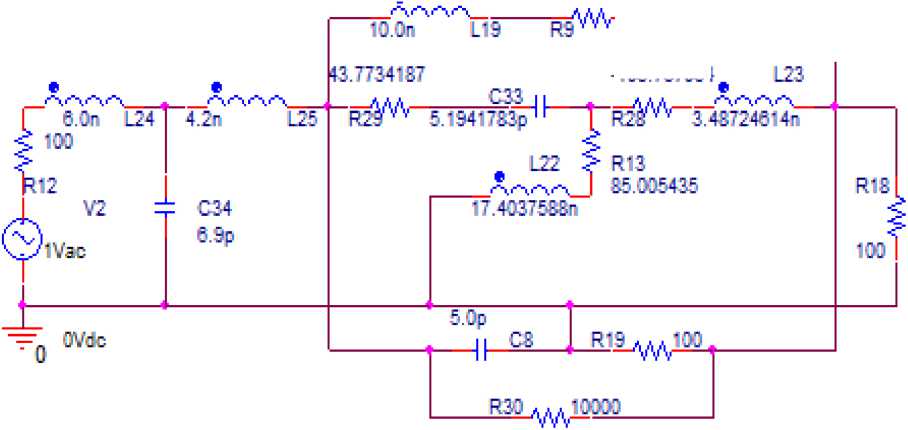
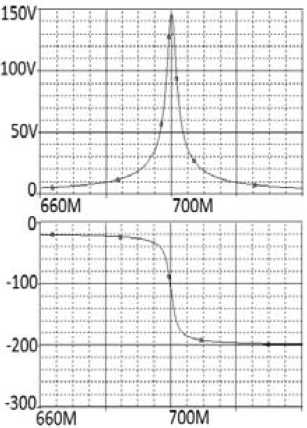
Рис. 6. Эквивалентная схема ( а ) однокаскадного узкополосного усилителя (рис. 5, а ), соответствующая структурной схеме (рис. 2, а ), и ее частотные характеристики ( б ), полученные в системе OrCad

Fig. 6. Equivalent circuit ( a ) of a single-stage narrow-band amplifier (Fig. 5, a ), corresponding to the structural diagram (Fig. 2, a ), and its frequency characteristics ( b ) obtained in the OrCad system

б

занным на рис. 1, а , 2, а , а также их теоретические и экспериментальные характеристики. Использован транзистор типа BFQ17PH (рис. 4, а , 5, а ). Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС в виде П-образного соединения трех элементов С б ₆, R 106 , R ₁₀ 8 , С 74 , R 113 , R _n5 на двухкаскадной схеме (рис. 4, а ) и С ₆₆, R 106 , R 108 на однокаскадной схеме (рис. 5, а ). Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₀₀ и R ₁₀₇ соответственно. Схемы РЧ собраны в виде Т-образного четырехполюсника на элементах L 5 , L 6 , C 70 , L 8 , L 9 , C 75 (рис. 4, а ), L 5 , L 6 , C 70 (рис. 5, а ), параметры которых определялись по формулам (24).

Эквивалентная схема нелинейного элемента выполнена в виде перекрытого Т-образного че- тырехполюсника на элементах R29, С33, R13, L22, R28, L23, R9, L19 (рис. 6, а). Параметры эквивалентной схемы НЭ выбраны из условия совпадения входного сопротивления НЧ с входным сопротивлением НЧ с использованием реального транзистора [1]. Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов С8, R19, R30. Параметры ЦОС заданы произвольно. Схема РЧ собрана на основе Т-образного соединения трех элементов L24, L25, С34.

Частотные характеристики принципиальных схем, показанных на рис. 4 и 5, идентичны. Это соответствует выводам, сделанным на основе анализа полученных выше выражений для передаточных

а

б

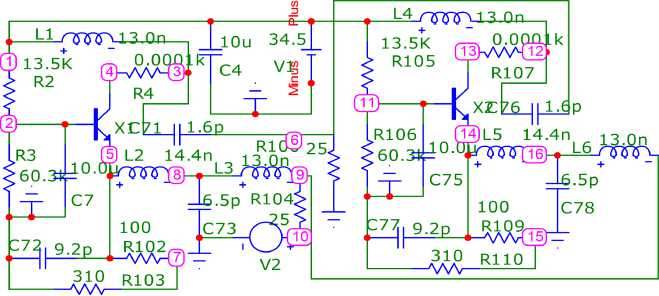
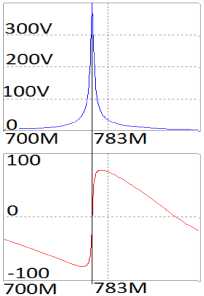
Рис. 7. Вторая принципиальная схема двухкаскадного узкополосного усилителя ( а ), соответствующая структурной схеме (рис. 1, а ), и его частотные характеристики ( б ), полученные в системе MicroCap

Fig. 7. The second schematic diagram of a two-stage narrow-band amplifier ( a ), corresponding to the structural diagram (Fig. 1, a ), and its frequency characteristics ( b ), obtained in the MicroCap system

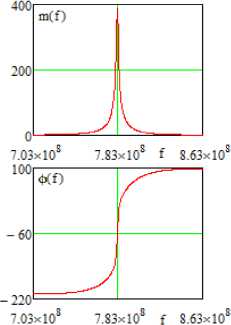
а

б

в

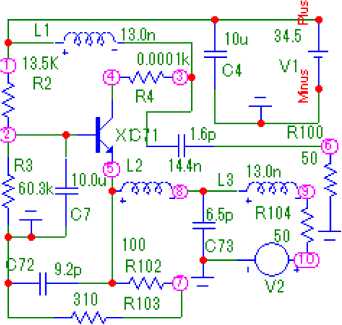
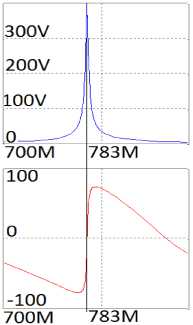
Рис. 8. Принципиальная схема однокаскадного узкополосного усилителя ( а ), соответствующая структурной схеме (рис. 2, а ), его частотные характеристики ( б ), полученные в системе MicroCap, и частотные характеристики его эквивалентной схемы, полученные в системе MathCad ( в )

Fig. 8. Schematic diagram of a single-stage narrow-band amplifier ( a ), corresponding to the structural diagram (Fig. 2, a ), its frequency characteristics ( b ), obtained in the MicroCap system, and the frequency characteristics of its equivalent circuit, obtained in the MathCad system ( c )

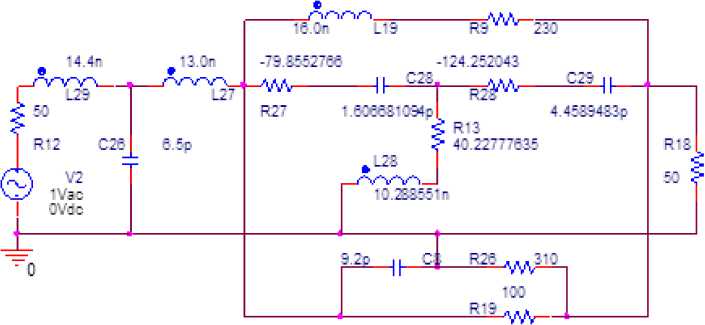
Рис. 9. Эквивалентная схема ( а ) однокаскадного узкополосного усилителя (рис. 9, а ), соответствующая структурной схеме (рис. 2, а ), и ее частотные характеристики ( б ), полученные в системе OrCad

Fig. 9. Equivalent circuit ( a ) of a single-stage narrow-band amplifier (Fig. 9, a ), corresponding to the structural diagram (Fig. 2, a ), and its frequency characteristics ( b ), obtained in the OrCad system

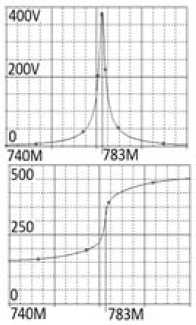
б

функций исследуемых структурных схем (рис. 1, а ). Анализ также показывает, что экспериментальные (рис. 4, б , 5, б ) частотные характеристики принципиальной схемы узкополосного усилителя (рис. 4, а , 5, а ) удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 6, а ) усилителя, полученные расчетным путем (рис. 5, в ) и экспериментально (рис. 6, б ). Резонансная частота эквивалентной схемы f ≈ 700 МГц (рис. 5, в и 6, б ) незначительно отличается от резонансной частоты принципиальной схемы f ≈ 697 МГц (рис. 4, б , 5, б ). Произведение коэффициента усиления на полосу частот составляет примерно 120 МГц.

На рис. 7–9 показана еще одна пара эквивалентных однокаскадной и двухкаскадной схем, но с другими значениями сопротивлений источника сигнала и нагрузки. В этих схемах с помощью описанной выше методики оптимизированы параметры двухполюсников не только РЧ, но и всех остальных двухполюсников. Произведение коэффициента усиления на полосу частот составляет примерно 500 МГц.

Таким образом, полученные математические модели РЧ-типа (22)–(25) могут быть использованы для технического проектирования различных радиоустройств с заданными частотными характеристиками.