Параметрический синтез различных радиоустройств с заданным количеством каскадов типа «нелинейная часть - резистивный четырехполюсник»

В работе [1] предложены алгоритмы параметрического синтеза плоско-слоистых сред (ПСС), содержащих заданное количество управляемых и неуправляемых слоев, по критерию обеспечения заданной амплитудно-фазовой модуляции рассеянного сигнала. Управляемые слои – это двумерно-периодические решетки проводящих стержней или полосок, в разрывы которых включены нелинейные элементы, управляемые низкочастотным сигналом. Неуправляемые слои (НС) – это однородные диэлектрические слои без потерь или двумерно-периодические решетки стержней или полосок. В общем случае ПСС функционирует в смешанном режиме – присутствует как отраженная, так и проходная волна. Если один из НС, расположенный последним по направлению

падающей волны, выполнен в виде проводящего экрана, то ПСС является отражающей. В этом случае ПСС может быть использована в качестве основы для построения перспективной курсоглиссадной системы [2]. Суть алгоритмов состоит в формировании систем алгебраических уравнений, отвечающих требованиям к системным операторам (коэффициентам отражения и передаточным функциям) в заданном количестве состояний, удовлетворяющих заданным уровням низкочастотного сигнала. Результатом решения этих уравнений является система взаимосвязей между элементами классической матрицы передачи некоторых НС, отнесенных к неуправляемой части. Оставшаяся часть НС отнесена к управляемой части ПСС. Система взаимосвязей – это исходная система уравнений для отыскания параметров НС.

ЕЭЕ^Ж © Головков А.А., 2024

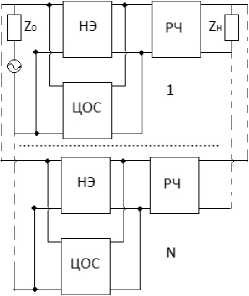
а

Рис. 1. Структурные схемы многокаскадных радиоустройств с параллельной по напряжению ( а ) и последовательной по току ( б ) цепями обратной связи, включенными между источником сигнала и РЧ

Fig. 1. Block diagrams of multi-stage radio devices with voltageparallel ( a ) and current-series ( b ) feedback circuits connected between the signal source and RF

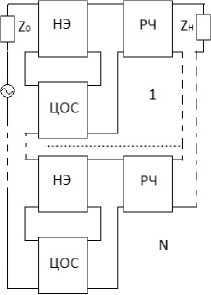
б

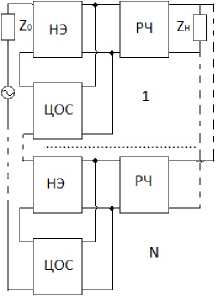
а

Рис. 2. Структурные схемы многокаскадных радиоустройств с последовательной по напряжению ( а ) и параллельной по току ( б ) цепями обратной связи, включенными между источником сигнала и РЧ

Fig. 2. Block diagrams of multistage radio devices with voltage-sequential ( a ) and current-parallel ( b ) feedback circuits connected between the signal source and RF

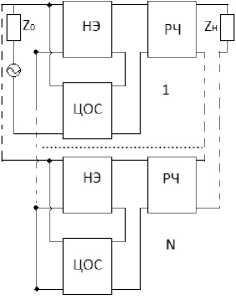
б

Разработанные алгоритмы могут быть использованы практически в любом диапазоне радиочастот. Отличие состоит лишь в реализации элементов классической матрицы передачи НС. В соответствующих диапазонах частот это могут быть элементы либо с распределенными [1; 2], либо с сосредоточенными параметрами [3–7]. Для реализации геометрических размеров неуправляемых и управляемых решеток ПСС [1; 2] необходимо привлечение результатов решения задач дифракции электромагнитных волн на различных проводящих телах [8].

Наиболее полно метод решения задач параметрического синтеза различных радиоустройств (за исключением многокаскадных) с обоими типами элементов изложен в работе [9].

В данной работе предлагается рассмотреть особенности этих алгоритмов с учетом наличия каскадов типа «нелинейная часть (НЧ) – резистивный четырехполюсник (РЧ)». Эти каскады включены между источником сигнала с сопротивлением z о = 10 + jx о и нагрузкой z _^ = r _^ + jx _H (рис. 1, 2). При этом учитывалось, что НЧ состоит из трехполюсного нелинейного элемента (НЭ) и охватывающей его цепи обратной связи (ЦОС – параллельной или последовательной по току или напряжению).

Оптимизация параметров двухполюсников, не входящих в КЧ, осуществляется с помощью известных численных методов [10] по критерию обеспечения заданной рабочей полосы частот. Все обозначения неописанных величин в данной статье соответствуют принятым в [9].

Алгоритм синтеза многокаскадных радиоустройств с учетом наличия каскадов типа «НЧ – РЧ» приведен в работе [11].

1. Результаты параметрического синтеза

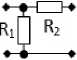
Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем РЧ при использовании параллельной по напряжению обратной связи (рис. 1, а ) и алгоритма синтеза [1–3] с учетом указанных изменений. Этот вид обратной связи допускает применение РЧ практически любой сложности. Если необходимо синтезировать радиоустройство с одинаковыми каскадами типа «НЧ – РЧ», а в качестве РЧ используется Г-образное соединение двух сопротивлений R ₁₂ (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом (аргументы опущены):

e x + R 2 d x

R i =-- ;

d x + e x + R 2 b x

- B 2 ± ^22 - 4 A 2 C 2

2 A ₂

где

• A 2 = b x d _r - b r d x ;

• B. = d (1 - e ) + b e - b e + d e ; x r xr rx rx

C = er ^{( d}x ⁺ ex) ^- cx ^{( d +} e ^{- 1 )-} rx x xr r

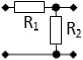
Обратное Г-образное соединение двух сопро тивлений R12 (рис. 3, б):

а

б

в

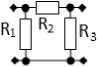
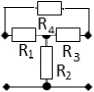
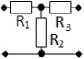
Рис. 3. Синтезированные РЧ

Fig. 3. Synthesized RF

а

б

Рис. 4. Синтезированные РЧ (продолжение)

Fig. 4. Synthesized RF (continued)

R1 =

c r ⁺ R 2 ⁽ d r ⁺ e r - 1).

1-Rbr   ;

(2)

R 2 =

- B2 ± BB- - 4 A 2 C2

2A2

C3 = bxR + (d + e + b c - b c )R + x x x rx xr

^{+ ( d} _r ⁺ e_r ^{- 1 ) c} _x ^- c_r ^{( d} _x ⁺ e_x ). r r x rx x

П-образное соединение трех сопротивлений

где

R12 3 (рис. 4, а):

A = ( d + e - 1) b - b ( d + e );

r r x rx x

B2 = dx + ex - brc + bc ;    C2 = c .

x x rx xr         x

Т-образное соединение трех сопротивлений

R12 3 (рис. 3, в):

_R _ ^cr ⁺ R 2^{( d}r ⁺ e r ⁺ R 3 ^br ^{- 1 +} R 3 ^dr .

R =

• ¹             1 - b r ( R 2 + R 3 )

„ _ - B 2 ± В B 2 - ⁴ A 2 C 2

Rq = где

A2 = (dr + er - 1b - br(dX + ex); r   r xrx x

By = dx + e - b c + b c - x  x  rxxr

- R3 [(2dx + ex)br - bx(2dr + er)];

x xr x r r

C2 = (bd - bd ) R - + (dx - be + bc ) R, + cx. x r r x       x rx xr x

(3)

_R = ^cr ^{+ R} 2^{( d}r ⁺ e r ^{+ R} 3 ^br ^{- 1 + R} 3 ^dr

• ¹             1 - b r ( R 2 + R 3 )

_p _ - ^B 3 ± В^B 3 - ⁴ A 3 ^C 3

Ro =,

• ³          2 A ₃

где

A 3 = bd - bA;

(4)

^B 3 = ^dx ^{- R} 2^{[( 2 d}x ⁺ e x ) ^br ^{- b}x ^{( 2 d}r ⁺ e r ^{)] - b}r c x ^{+ b}x c r ;

^C 3 = ^{[( d}r ⁺ er ^- 1 ) ^bx ^{- b}r ^{( d}x ⁺ ex ^{)] R} 2 ⁺ r r x rx x

^{+ ( d}x ⁺ e x ^- brcx ^{+ b}x cr ) R 2 ⁺ c x .

R = ^{( 1 - R} 3 ^br ) ^R 1 ^{- c} r ^{- R} 3 ^dr _;

(R1 + R3 )br + dr + er -1

„ _ - B 3 ± В B 3 -4 A 3 C 3

r^=,

3         2A3

где

A3 = brdx - bxdr;

B3 = brcx - bxcr - R. (brex - bxer) - dx - drex + dxer;

rx xr     rx xr   x rx xr

^{( c}r ^{+ R} 2 ^dr ) ^R 3 ^{+ R} 2 ^cr

1   R 2 - cr - R 3( dr + er + R 2 br - 1
- B ± 2	ВB 22 - 4 A 2 C 2
	2 A 2
где
A 2 = ( bxdr -	’ brdX ) R 3 + ( d X - brcX + b X c ) R 3 + c X ; r x       x rx xr      x
B 2 = ( d x - br	. c + b c + d e - d e ) R 3 + x xr rx xr
+ (2 c x + c r e x	: - c x e r ) R 3;
C 2 = R 3[( dx	+ e x ) c r - c x ( d r + e r - 1 )] .
R         ( c	r + R 2 dr ) R 3 + R 2 cr      .
1    R 2 - c r	- R 3 ( d r + e r + R — b r - 1)
- B o ± R 3 =    3	В B 3 - 4 A 3 C 3
	2 A 3
где
A 3 = ( bxdr -	' brdX ) R 2 + ( d X + e X ) cr - c X ( dr + er - 1) + rx        x x r x r r
+ ( d x - b r c x	+ bxcr + drex - dxer ) R o; xr rx xr
C 3 = R 2 c x ;
B 3 = ( d x - br	■ cx + bxcr ) R 2 + ( 2 cx + c r e x - c x e r ) R 2 .
R = R <( 1 -	d r - e r ) - c r ( R 1 + R 3 ) _
2       c r -	R 1 + R 3 ( d r + R 1 b r )    ;
- B o ± R 3 =    3	В B 3 - 4 A 3 C 3
	2 A 3

где

A = (bx + brdx - bxdr + brex - bxer)R22 - crdx + cxdr + x rx xr rx xr rx xr

+ (dx + bcx - bxcr + drex - dxer) R.;

x rx xr rx xr

C 3 = ^{- R} 2 c x ^;

B3 = R. (c e - c e ) - R2 (d + e - b c + b c ). rx xr      x x rx xr

(6)

(7)

(8)

Перекрытое Т-образное соединение четырех со-

противлений R12 3 4 (рис. 4, б):

r    [R 2 (1 - d r - e r ) - c r ^]( R 3 + R 4 ) - R 3 R 4 ⁽ d r + b r R 2 ).

1         c r - R 4 + ( R 2 ⁺ R 3⁾⁽ d r ⁺ e r ⁺ b _r ^R 4 - 1)

R 2 =

- B 2 ± A² - 4 A 2 C 2

2 A2

где

A2 = [(dr + er - 1) bX - br(dx + ex)] R2 ; r   r xrx x

B2 = [dx + ex - brcx + bxcr + R3B0]R2 + x  x  rxxr

+ R 3 R 4 ^[( d + 1)e_x ^- dx ⁽ er ^{- 2 )];} r x xr

B _o = b_x (2 d + e _r) - b (2 d_x + e_x );

xrr rx x

C 2 = C x R 4 (2 R 3 + R 4 ) +

⁺ R 3⁽ R 3 ⁺ R 4^)[( d x ^- b r c x ⁺ b x c r ) R 4 ⁺ c r e x ^- c x e r ^{] +}

+ R 2 [( b_xd_r - b_rd_x ) R 2 + xr rx

^{+ (} d r e x ^- d x e r ) ^R 4 ⁺ c x ⁺ c r d x ^- c x d r ]•

^R 1 = ^{[ R 2^{( 1 -} d r ^{- e} _r ) ^{- c} _r ^{]( R} 3 + R 4 ) ^{-                   (10)}

• ^- R 3 R 4⁽ d r + ^b_r^R2 ^)} / ^{{ c} _r ^{- R} 4 ⁺

+ ⁽ R 2 + R 3⁾⁽ d r + e r + b _r ^R 4 ^- 1)J;

• „ _ - ^B 3 ± J B 3 - ⁴ A 3 ^C 3

R-r = ,

• ³          2 A ₃

где

A 3 = ⁽ bxd ^- brdx ) ^{R 2 +} cx ^{( 1 -} d ^- er ) ⁺ cr ⁽ dx ⁺ ex ) ⁺ xr rx x r r r x x

+ ( d_x - b_rc_x + b_xc_r + d_re_x - d_xe_r ) R ₄;

x rx xr rx xr

B 3 = ⁽ dx ^- brcx ⁺ bxcr ) ^{R 2 + ( 2} cx ⁺ crex ^- cxer ) R ^{2 -} x rx xr       x rx xr

• -    { R ₂ [ R 2 [(2 d_x + e_x )b_r - b_x (2 d _r + e _r)] - B _o]; x xr x r r

B o = R ^{2 [(} dr ⁺ 1) ex ^- dx ⁽ er ^{- 2 );} r x xr

^C 3 = ^{[ bx ⁽ dr ⁺ er ^- 1) ^- br ⁽ dx ⁺ ex ^{)] R 2 + C} O ⁺ cx ^{} R 2;} xr r     rx x        x

C o = ( dx + e_x - b_rCx + b_xc_r ) R 2 x x rx xr

^R 1 = ^{{[ R}2 ^{( 1 -} d r ^{- e} _r ) ^{- c} _r ^{]( R} 3 ^{+ R} 4 ) ^-

^{- R} 3 ^R 4⁽ d r + ^b _r ^R 2^)} / ^{{ c} _r ^{- R} 4 ⁺

+ ⁽ R 2 + ^R 3⁾⁽ d r + e r + b r R 4 ^- 1 ^)};

• -    R 3 R ₄ ( d r + b _r R 1 )}/

I ( R 1 + R 3 + R 4 )( d r + e r - 1) + b r R 4 ( R 1 + R 3 );

• „    _ - B 3 ± ] B 3 - ⁴ A 3 ^C 3

R o =---------------------,

• ³          2 A ₃

где

A3 = (bxdr - brdx)R2 + Cx (1 - dr - er) + Cr (dx + ex) + xr rx x r r r x x

+ ( d_x - b_rc_x + b_xc_r + d_re_x - d_xe_r ) R ₄;

x rx xr rx xr

B 3 = ( R 1 + R ₄)[ R ₄( d r e x - d x e r ) -

• ^{-    2} c ⁽ d + e — 1) + ² c ⁽ d + e ^)] + xr r     rx x

+ ^[ dx ^{+ R} 1⁽ brex ^- bxer ^{)] R 2 -} x rx xr

• ^{-    R} 4^{[( R} 4 ^{- 2} R ^{)( b} _r ^c _x ^- bxcr ) ^{- e}x^R4 ^]; rx xr x

• C 3 = (R1 + R)2 [(dx + ex )cr - cx(dr + er -1)] - bxR2R2 -x xr x r rx

• ^{- R} 1 ^R 4^{( R} 1 ^{+ R} 4^{)( d}x ⁺ ex ⁺ brcx ^- bxcr ^); x x rx xr

R2 = {(R3 + R4)(R1 - cr)- [cr + R3(dr + er)]R1 -

- R 3 R ₄ ( d r + b _r R 1 )}/

I ^{{( R} 1 + ^R 3 + ^R 4⁾⁽ d _r + e _r ^- 1) + ^b _r ^R 4^{( R} 1 + ^R 3^)};

_ _ - B4 ± bb4 -4 A 4 C 4 R, где

A 4 = ^{( c} _r ^{- R} 1^{)( d} _x + ^e _x ) +

+ cx ^{( 1 -} dr ^- er ) ^{- R 2 (} brdx ^- bxdr ) ^- x r r      rx xr

• ^{- b}x^Rl ^{+ R} 3 ^[ dx ^{+ R} 1⁽ brex ^- bxer ) ⁺ drex ^- dxer ^{] -} x       x rx xr rx xr

• ^{- (} b r c x ^- b x c r ^{)( R} 1 ^{+ R} 3 );

B 4 = ⁽ b x C r - b r C x ^{)( R} 1 + ^R 3⁾² +

+ ^{[ R} 3 ⁽ drex ^- dxer ) ^{- 2} cx ⁽ dr ⁺ er ^- 1) ^{+ 2} cr ⁽ dx ⁺ ex ) ^- rx xr x r r        r x x

• ^- e x^R1 ^{]( R} 1 ^{+ R} 3 ) ^{+ ( R} 3 ^- R ² ) d x ^;

• ^C 4 = ^{( R} 1 + ^R 3^{)2 [( 1 - e} _r ^- d ^)c _x ⁺ cr ^{( d} _X ⁺ e_X ^)] r rx rx x

• ^R 3 = ^{{[( 1 - d} _r ^{- e} _r ) ^R2 ^{- c} _r ^{)]( R} 1 ^{+ R} 4 ) ^{-                   (14)}

  R ₄ =

  
  

  - B ₄ ± ^ B 4 - 4 A ₄ C ₄

  2 A ₄

  
  

где

A4 = ⁽ bxdr ^- brdx ⁾⁽ R 2 ^{+ R} 3 ^{)2 + (} dx ⁺ ex ) R 2 ^{- b}x^R 2 ⁺ xr rx             x x x

• ⁺ c x ⁺ d x^R 3 ^{+ [} b x c r ^- b r c x ^{- R}2 ⁽ b r e x ^- b x e r ^{)]( R}2 ^{+ R} 3 ^

B 4 = ⁽ d x ^- b r c x ⁺ b x c r ) ^R 3 ^{+ [ 2} c x ⁺ c r e x ^- c x e r ⁺ B 0^{] R} 3 ;

B _o = R ₂ (2 d_x + e ) + ( d_re_x - d_xe_r )( R ₂ + R ₃);

x x rx xr

C ₄ = [ c_x (1 - d_r - e _r) + c _r ( d_x + e_x )] R 2 ; x r r rx x

- R 1 R ₄ ( b _r R ₂ - 1)}/

/ ^{ c _r + d _r ^R 4 + ^{( R} 1 + ^R 2⁾⁽ d _r + e _r + b _r ^R 4 ^{- 1 )};}

R ₄ =

- B ₄ ± J B 4 - 4 A ₄ c ₄

2 A ₄

где

A = b (R. + R. )^ - crdx + cxd + R2 (brdx - bxdr) + x          rx  xr     rx xr

+ (Rx + R2)[d + R2 (b e - b e ) + bc - bc ] + x rx xr rx xr

• + R ₂ ( d r e x - d x e r );

• B4 = ^{R 2 ( d} _X ^{+ e} _X ^{+ b}r^C_X ^{- b}_X^Cr ) ^- x x rx xr

  — \2c d — 2c d ^ с c — с c —

  1 rx xr rx xr

  
  

  - ^R 2^{( 2} d x + e x + d r e x - d x e r ^)] ;

  C 4 = [( d_r + e_r - 1) c_x - c_r ( ^d _x + e_x )] ^R • r r x rx x

  
  

  Пусть теперь требуется синтезировать радиоустройство с неодинаковыми каскадами типа «НЧ– РЧ». Если в качестве РЧ используется Г-образное соединение двух сопротивлений R ₁₂ (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом:

  
  

  ^- b r⁽ c x ^- c 1 x ^{+ 2 d} 1 x ^{)] R} 3 ⁺

  ^{+ (} c x ^- c 1 x ^{+ d} 1 x ^)dr ^{- d}x ⁽ c r ^- c 1 r ^{+ d} 1 r );

  C 2 = ⁽ b x^d 1 r ^- b r^d1 x ) ^R 3 ⁺

  ^{+ (} b x c 2 r ^- b r c 2 x ^{+ d}r^d1 x ^{- d}x^d1 r ) ^R 3 ^- c 2 r^dx ⁺ c 2 x^dr • •

  
  

  R 1 =

  
  

  c 2 r + ^R 2 ^d 1 r _______.

  c 1 r - c r + d r - ^d 1 r - R 2 br

  
  
  
  

  _D   - B 2 ± J В 2 - ⁴ A 2 C 2

  R o =----------------

  ²           2 A ₂

  где

  
  

  r = c 2 r ^{+ R} 3 ^d 1 r ⁺ R 2⁽ C d ^{+ R} 3 b r ) .

  • ^{1          d}r ^{- ( R} 2 ^{+ R} 3 ) b r

  „ _ - ^B 3 ± ^B 3 - ⁴ A 3 C 3

  Ro =---------------------,

  • ³          2 A ₃

  где

  A 3 = b r^d1 x ^- b x^d1 r ^;

  ^B 3 = b r c 2x ^- b x c 2r ⁺ R 2 ^[( c x ^- c 1 x ^{+ 2 d}1 x ) b r ^-

  
  

  b x ⁽ c r    c 1 r ^{+ 2 d} 1 r ^{)] + d}x^d1 r   ^dr^d1 x ^;

  
  
  
  

  A 2 = b r^d1 x - b x^d1 r ^;

  ^B 2 = ⁽ c r - c 1 r - d r ) d 1 x +

  + ^d 1 r ⁽ c 1 x ^- c x + d x ) + b r c 2 x - b x c 2 r ^;

  
  

  C 2	C d	c 2 x -	Co D : 2 r c ;
  C d	= c r	- c 1 r	- d r + d 1 r ;
  D c	= c x	- c 1 x	- dx + d 1 x

  •

  
  

  Обратное Г-образное соединение тивлений R ₁₂ (рис. 3, б ):

  R = c 2 r ^{+ R} 2 C d .

  ¹ d - Rb ’

  
  

  двух сопро-

  
  
  
  

  C 3 = ⁽ D c b r ^- b x C d ) ^{R 2 + [(} c 1 x ^- c x ^{- d} 1 x ) ^dr ⁺

  ^{+ d}x ⁽ c r ^- c 1 r ^{+ d}1 r ) ⁺ b r c 2x ^- b x c 2r ^{] R}2 ⁺

  ⁺ c 2r d x ^- c 2x d r •

  r = ^{( d}r ^{- R} 3 b r ) ^R 1 ^- c 2 r ^{- R} 3 ^d 1 r .

  • ^{2        ( R} 1 + ^R 3 ) b r + C d      ’

  _p _ - ^B 3 ± V ^B 3 - ^{4 A} 3 C 3

  R o =,

  • ³          2 A ₃

  где

  A 3 = b r^d1 x ^- b x^d1 r ^;

  ^B 3 = b r c 2x ^- b x c 2r ^{- R} 1^[( c x ^- c 1 x ) b r ^-

  
  
  
  

  ■ 2 -

  Bl ±’ 2	B 2
  R 2
  	2 A 2
  где
  A2 = b r D c -	b x C d ;
  B 2 = ( c 1 x - c	x - d1 x
  + dx ( c r - c 1 r	+ d 1 r )

  ) d r +

  r c 2 x

  C 2 = c 2 r d x

  
  

  2 C 2

  ,

  
  

  _-

  
  

  b x c 2 r ;

  
  

  _-

  
  

  c 2 x dr •

  
  

  Т-образное соединение трех сопротивлений

  
  

  R _{12 3} (рис. 3, в ):

  R = c 2 r ^{+ R}3 ^d1 r ^{+ R}2 ⁽ C d ^{+ R} 3 b r )

  ^{1          d}r - ^{( R} 2 ^{+ R} 3 ) b r

  
  
  
  

  ^- b x ⁽ c r ^- c 1 r ^{)] + (} c r ^- c 1 r ^- d r ^)d1 x ^{+ d} 1 r ⁽ c 1 x ^- c x ^{+ d}x ^);

  
  

  C 3 = ⁽ b x^dr   b r^dx ) ^R 1 ⁺ C d c 2 x   D c c 2 r ^{+ [} b r c 2 x

  ^- b x c 2 r ^{+ (} c x ^- c 1 x ^{+ d}1 x ) d r ^{- d}x ⁽ c r ^- c 1 r ^{+ d}1 r ^{)] R} 1 •

  
  

  П-образное соединение трех сопротивлений

  
  

  R _{12 3} (рис. 4, а ):

  
  

  ^{( R} 2 + ^R 3 ) c 2 r + R 2 ^R 3 ^d 1 r ,

  R =------------------------ ;

  ^R 2 ^dr ^- c 2 r ^{- (} C d ^{+ R} 2 b r ) ^R3

  
  

  „ _ - B 2 ± JB 2² - 4 A 2 C 2

  R o =---------------------,

  ²           2 A ₂

  где

  A 2 = ⁽ b r^d1 x ^- b x^d1 r ) ^R 3 ^{+ (} brc 2x ^- b x c 2 r ^-

  
  
  
  

  „ _ - B 2 ± J B 2² - 4 A 2 C 2

  Ro =---------------------,

  ²           2 A ₂

  где

  A 2 = b x C d - b r^Dc ;

  
  

  ^{- d}r^d1 x ^{+ d}x^d1 r ) ^R 3 ⁺ c 2x C d ^- c 2r^Dc ^;

  A 0 = ^[( c 1 x ^- c x ^{+ 2 d}x ^{) c} 2 r ^- c 2 x ⁽ c 1 r ^- c r ^{+ 2} d r ^{)] R} 3^;

  ^B 2 = ^[ brc 2x ^- b x c 2 r ^{+ B} 0^{] R} 3 ⁺

  ^{+ [(} c 1 x ^- c x ^{+ 2 d}x ) c 2 r ^- c 2 x ⁽ c 1 r ^- c r ^{+ 2} d r ^{)] R} 3^;

  ^B 0 = ⁽ c r ^- c 1 r ^- d r ^{) d} 1 x ^{+ d}1 r ⁽ c 1 x ^- c x ^{+ d}x ^);

  
  

C2 — (c 2 xCd c 2 rDc) R 3 • r — (R2 + R3)c 2 r + R2 R 3 d1 r .

1 R 2 d r - ^c 2 r - ⁽ C d + R 2 b r ) R 3

„ _ - B 3 ± ] B 3 - ⁴ A 3 C 3

R o —--------------------- ,

• ³          2 A ₃

где

A 3 ^{— (} b r^d1 x - b x^d1 r ) R 2 + ⁽ b r^c 2 x - b x^c 2 r + A 0 ) ^R 2 + + ^c 2 x C d - ^c 2 r D c ^;

A 0 = ^{( c}r - ^c 1 r - ^dr ) ^d1 x + ^d1 r ^{( c} 1 x - ^cx + ^dx ^);

B 3 = ^[ b r^c 2 x - b x^c 2 r - ^dr^d1 x + ^dx^d1 r ^{] R} 2 +

+ ^{[( c} 1 x - ^cx + ^{2 d}x ) ^c 2 r - ^c 2 x ^{( c} 1 r - ^cr + ^{2 d}r ^{)] R} 2^;

C 3 ^{— ( c} 2 r^dx - ^c 2 x^dr ) R 2 •

R _—   ⁽ R + R 3 ) c 2 r + ^R1 R 3 C d .

• ^{2   ( d}r - ^R 3 br ) R 1 ^{- c} 2 r - ^R 3 ^d 1 r

„ _ - B 3 ± ] B 3 - ⁴ A 3 C 3

R o —--------------------- ,

• ³          2 A ₃

где

A 3 ^{— (} D c b r ^- b x C d ) R 2 ^{+ (} b r^c 2 x ^- b x^c 2 r ⁺ A 0 ) R 1 ^{-- c} 2 r^d1 x ^{+ c}2x^d1 r ^;

A 0 ^{— ( c} 1 r ^{- c}r ⁺ d r ) ^d 1 x ^{- d} 1 r ^{( c} 1 x ^{- c}x ^{+ d}x ^);

B 3 ^— R 2 ^[ b r^c 2 x ^- b x^c 2 r ^{+ ( c} 1 x ^{- c}x ^{- d} 1 x ^)dr +

^{+ d}x ^{( c}r ^{- c} 1 r ^{+ d} 1 r ^{)] -} R 1 [ ^{( c}r ^{- c} 1 r ) ^c2x ^{- c}2r ^{( c}x ^{- c} 1 x ^)];

C 3 ^{— ( c} 2 r^dx  ^c 2 x^dr ) R 2 •

Перекрытое Т-образное соединение четырех со-

C 2 ^{— {(} b x^d1 r ^- b r^d1x ) R 4 ^{+ [( c}x ^{- c} 1 x ^)d1 r ^-

• ^{-    d}1 x ^{( c}r ^{- c} 1 r ^)] R 4 ^{+ c}2r^d1 x ^{- c}2x^d1 r } R 3 ^-

• ^{-    ( c} 2 r d x ^{- c} 2 x d r ⁾⁽ R 3 ⁺ R 4^{)2 -}

• ^{-    (} R 3 ⁺ R 4^)[ R 4⁽ b r^c 2 x ^- b x^c 2 r ^-

• ^{-    d}r^d1 x ^{+ d}x^d1 r ) ⁺ C 0^] R 3^;

C 0 ^{— ( c}r ^{- c} 1 r ^{) c} 2 x ^{- c} 2 r ^{( c}x ^{- c} 1 x ^);

C d ^{— c}r ^{- c} 1 r ^{- d}r ^{+ d}1 r ;

D c ^{— c}x ^{- c} 1 x ^{- d}x ^{+ d} 1 x •

_{R —} ⁽ C d R 2 + c 2 r X R 3 + R 4 ) + R 3 R 4^{( d} 1 r + R 2 b r )

• ¹        R 4 d r ^{- c} 2 r ^{- (} C d ⁺ R 4 b r ⁾⁽ R 2 ⁺ R 3 )

„ _ - B 3 ± V B 3 - ⁴ A 3 C 3

R ^{3 —}       2 A      ’

где

A 3 ^{— ( c} 2 r ⁺ R 4 ^d1 r ^{)( c}x ^{- c} 1 x ) ^{- ( c}r ^{- c} 1 r ^{)( c} 2 x ⁺ R 4 ^d1 x ) ^-

• ^{-    (} b r^d1 x ^- b x^d1 r ) R 4 ⁺ R 4⁽ b r^c2x ^- b x^c2r ^{- d}r^d1 x ^{+ d}x^d1 r ) ⁺

^{+ c} 2 x ^{( d}r ^{- d} 1 r ) ^{- c} 2 r ^{( d}x ^{- d} 1 x ^);

B 3 ^— B 0 ^{- 2} R 4^{( c} 2 r^dx ^{- c} 2 x^dr ) ^-

• -    [2 R 2 ( b r^d 1 x - b x^d1 r ) + b r c 2 x - b x c 2 r ] R 4 ;

B 0 — [(2 R 2 + R 4 )( d _r d 1 x - d _x d 1 r ) + B ₀₁ ] R 4 ;

B 01 ^{— ( c}x ^{- c} 1 x ^{)[ c} 2 r ⁺ R 2^{( d}r ^{+ d} 1 r ^{- R} 4 b r ^{)] -}

• ^{-    ( c}r ^{- c} 1 r ^{)[ c} 2 x ^{+ R} 2^{( d}x ^{+ d} 1 x ^{- R} 4 b x ^)];

C 3 ^{— {[} C 0 ^{+ ( d}r ^- R 2 b r ^{)( c}x ^{- c} 1 x ^{+ d} 1 x ^{)] R} 2 ⁺

• +    ( b r d x - b x d r ) R 2² + c 2 x d r - c 2 r^dx } R 4 5

C 0 ^— b x^c 2 r ^- b r^c2x ^{- ( d}x ^{- R} 2 b x ^{)( c}r ^{- c} 1 r ^{+ d}1 r ^).

противлений R _{123 4} (рис. 4, б ):

R _— < C d R 2 + c 2r ) ⁽ R 3 + R 4 ) + R 3 R 4^{( d} 1 r + R 2 b r ) ¹       R 4 d r ^{- c} 2 r ^- ( C d ⁺ R 4 b r ⁾⁽ R 2 ⁺ R 3 )

R ₂ —

- B 2 ± B Dl - 4 A 2 C 2

2 A2         ’ где

• A 2 — ⁽ b x C d - b r D c ) R 4 ;

B 2 ^{— (} b x^c 2 r ^- b r^c 2 x ⁺ B 0 ) R 4 ^-

• ^-    R 3 R 4 [ ⁽ c r ^{- c} 1 r ^{)( d}x ^{+ d}1 x ) ^-

• ^{-    ( c}x ^{- c} 1 x ^{)( d}r ^{+ d}1 r ) ^{+ 2 ( d}x^d1 r ^{- d}r^d1 x ^)];

B 0 ^{— (} R 3 b x ^{- d}x ^{)( c}r ^{- c} 1 r ^{+ d} 1 r ) ⁺

^{+ (} d r ^- R 3 b r ^{)( c}x ^{- c} 1 x ^{+ d} 1 x ) ^-

• -    R 3 ( b r^d1 x - b x^d1 r );

( C d^R2 + c 2r )( ^R 3 + ^R 4 ) + ^R 3 ^R 4 ( ^d 1 r + ^R2 b r ) R 4 d r - c 2r - ( C d + R 4 b r )( R 2 + R 3 )

R ₄ —

- B 4 ± J B 4 - 4 A ₄ C ₄

2 A ₄

где

A4 — (brdx - bxdr)R22 + (drd1 x - dxd1 r)R3 -

• ^{-    R} 2 ^{{[ d}x ^- b x ^{( R}2 ^{+ R} 3^{)]( c}r ^{- c} 1 r ^{+ d} 1 r ) ^- A 0 } ^-

• ^{-    ( R} 2 ^{+ R} 3^{)[ R} 3^{( b}r^d1 x ^{- b}x^d1 r ) ^{+ b}r^c 2 x ^-

• ^-    b x^c 2 r ^{] - c} 2 r^dx ^{+ c}2x^dr ^;

A 0 ^{— [ d}r ^- b r ^{( R} 2 ^{+ R} 3^{)]( c}x ^{- c} 1 x ^{+ d} 1 x ^);

B 4 ^{— [} B 0 ^{- 2 ( c} 2 r^dx ^{- c} 2 x^dr ^{)] R} 3 ^{- R} 3^{( b}r^c 2 x ^{- b}x^c 2 r ^);

B 0 ^{— [( 2 R} 2 ^{+ R} 3^{)( d}r^d1 x ^{- d}x^d1 r ) ⁺

^{+ ( c}x ^{- c} 1 x ^{)[ c} 2 r ^{+ ( R} 2 ^{+ R} 3 ) ^d1 r ^{+ R} 2 ^dr ^{)] -}

• -    ⁽ c r - ^c 1 r ^)[ c 2 x + ^d 1 x ⁽ R 2 + R 3 ) + R 2 d x ^];

C 4 = ⁽ c 2 r^Dc - c 2 x C d ) R 3 •

R 2 = { R 4 [ R 1 d r - R 3 ( d 1 _r + R 1 b r )] -                      (26)

• —    C 2 r ⁽ R 1 + R 3 + R 4 ) — C d^R1^R 3 ^}/

I {( R 1 + R 3 + R 4 ) C_d + R 4 ( R 1 + R 3 )b r };

„ _ - B 3 ± J B 3 - ⁴ A 3 C 3

Rq =,

• ³          2 A ₃

где

A 3 = ⁽ c 2 r ⁺ R 4 ^d 1 r ⁾⁽ c 1 x ^- c x ^{+ d}x ) ⁺ R 4⁽ b r c 2 x ^- b x c 2 r ) ⁺

• ^{+ (} b r^d1 x   b x^d1 r ) ^R4   c 2 r^d1 x ⁺ c 2 x^d1 r

• ^{-    (} c 2 x ^{+ R} 4 ^d1 x ⁾⁽ c 1 r ^- c r ⁺ d r ^);

B 3 = [ R 1 R 4 ( d r - R 4 b r ) -

• ^{-    ( R} 1 + ^R 4 ⁾⁽ 2 c 2 r + ^R 4 ^d 1 r ^)]( c x ^- c 1 x ) +

^{+ (} c r ^- c 1 r ^{)[( 2} c 2 x ^{+ R} 4 ^d 1 x ^{)( R} 1 ^{+ R} 4 ) ^-

• -    ^R 1 ^R4 ^{( d} _x ^{- R} 4 ^b _x ^{)] - ( R} 1 ^{+ R}4 ^{)[( 2 c} 2 _x ^{( d} _r ^{- d} 1 _r ) ^-

• ^{-    2} c 2 r ^{( d}x ^{- d} 1 x ^{)] - R} 4^{( d}r^d1 x ^{- d}x^d1 r ) ⁺

+ ^R 4^{( 2 R} 1 + ^R 4⁾⁽ b r c 2 x ^- b x c 2 r ^);

C 3 = ⁽ C 2 x C d - C 2 r^Dc ^{)( R} 1 + ^R 4⁾² +

^{+ R} 1 ^R 4^{( R} 1 ^{+ R} 4^{)[( c} _x - ^c 1 _x ^{+ d} 1 _x ^)d _r ⁺ C 0^{] -}

• -    R 1² R 4 ( b _r d _x - b _x d _r );

C 0 = b r c 2x - b x c 2r ^{- d}x ⁽ c r ^- c 1 r ^{+ d} 1 r ^).

R 2 = { R 4 [ R 1 d r - R 3 ( d 1 _r + R 1 b r )] -

- c 2 r ( R 1 + R 3 + R 4 ) - C d R 1 R 3 }/

I {( R 1 + R 3 + R 4 ) C d + R 4 ( R 1 + R 3 ) b r };

R ₄ =

- B 4 ± J B 4 - 4 A 4 C 4

2 A ₄

где

A 4 = ⁽ c 2x ^{- R} 1 ^dx ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ) ^{+ R} 1⁽ b r c 2x ^- b x c 2r ) ^-

^{- (} br^d_X ^- b x d r ) ^R1 ^{+ ( b}r^d1 x ^- b x^d1 r ) ^{R 2 +} c 2r^dx ^- c 2x^dr ^-

• ^{-    (} c 2r ^{- R} 1 d r ⁾⁽ c x ^- c 1 x ^{+ d} 1 x ) ⁺

^{+ R} 3^[( c 1 x ^- c x ^{+ d}x ^)d1 r ⁺ A 0 ⁺ b r c 2x ^- b x c 2r ^];

A 0 = ^R 1^[ b x ⁽ c r ^- c 1 r ) ^- b r ⁽ c x ^- c 1 x ^{)] - d}1 x ⁽ c 1 r ^- c r ⁺ d r ^);

B 4 = ^{ B 0 - ^R3 ^{[ d} 1 x ^{( c} 1 r ^- c r ⁺ d r ) ^-

• ^{-    d} 1 r ⁽ c 1 x ^- c x ^{+ d}x ) ^{- b}r^c 2 x ^{+ b}x^c 2 r ^{]}( R} 1 ^{+ R} 3^);

B 0 = ^{( 2} c 2 x ^{- R} 1 ^dx ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ) ^-

• ^{-    ( 2 c} 2 r ^{- R} 1 ^dr ⁾⁽ c x ^- c 1 x ^{+ d} 1 x ) ⁺

^{+ R} 1^{( b}_rc 2 x ^{- b}x^c 2 r ) ^{+ 2 (} c 2 x^dr ^{- c} 2 r^dx ^);

C 4 = ( C 2x C d - C 2 r D c )( ^R 1 + ^R 3 ) 2 •

( d r - R 2 b r ) R 1 R 4 - ( R 1 + R 4 )( C d R 2 + c 2 r ) . ( C d + R 4 b r )( R 1 + R 2 ) + C 2 r + R 4 d 1 r   ’

R ₄ =

- B 4 ± 7 B 4 - 4 A ₄ C ₄

2 A ₄

где

A 4 = ^{R 2 ( b}r^d1 x ^{- b}x^d1 r ) ^{- C} 2 r^d1 x ^{+ C} 2 x^d1 r ⁺

^{+ {[ d}1 _x ^{+ b} _x ^{( R} 1 ^{+ R} 2^{)]( C} 1 _r ^{- C} _r ^{+ d} _r ) ^-

• ^-    A 0^{[ d} 1 _r ^{+ b} _r ^{( R} 1 ^{+ R} 2^{)]} R} 2 ^{+ R} 1⁽ d _r^d1 _x ^{- d}_x^d1 _r ) ^-

• ^{-    ( R} 1 ^{+ R} 2^{)[ R} 1⁽ b r d x - ^bx^dr ) - ^br^C 2 x ^{+ b}x^C 2 r ^] ;

• A 0 = ^{( C} 1 x ^{- C}x ^{+ d}x ^);

B 4 = ^{ B 0 ^{- [ C} 2 r ^{- d}r ^{( R} 1 ^{+ R}2 ^{)]( C}x ^{- C} 1 x ^{+ d} 1 x ^{)} R} 1 ⁺

• ^{+    R} 2 ^{( b}r^C 2 x ^{- b}x^C 2 r ^);

B 0 = ^{[ C} 2 x ^{- d}x ^{( R} 1 ^{+ R}2 ^{)]( C}r ^{- C} 1 r ^{+ d}1 r ) ⁺

• ^{+    d}1 r^(C2 x^{- R}2 ^dx)^{- d}1 x^(C2 r^{- R}2 ^dr) ^-

• ^{-    R}2^[(Cr^{- C}1 r)^d1 x^{- d}1 r^(Cx^{- C}1 x^)];

2. Математическое и схемотехническое моделирование

C 4 = ⁽ C 2 x C d - C 2 r D C ) ^R 12 •

Оптимизация значений сопротивлений двухполюсников РЧ, входящих в правую часть формул (1)–(28), производится с помощью известных численных методов [10].

На рис. 5–11 для примера показаны принципиальные и эквивалентные схемы однокаскадного и двухкаскадного усилителя, соответствующие исследуемой структурной схеме с параллельной по напряжению связью, представленной на рис. 1, а , а также их теоретические и экспериментальные характеристики. Использован транзистор типа BFQ17PH (рис. 5, а , 6). Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС (П-образного соединения трех элементов C 78 , R 105 , R 110 ) на однокаскадной схеме (рис. 5, а ) и C 78 >  R 105 , ^R 110 , C 82 , R 123 >  R 124 на двухкаскадной схеме (рис. 6). Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₁₄ и R ₁₁₇ соответственно. Схемы РЧ собраны в виде Г-образных четырехполюсников на элементах R 118 ’ R 119 ^(рис. ⁴⁾, R 118 , R 119 , R 127 ’ R 128 ^(рис. ⁶⁾, параметры которых определялись по формулам (1).

Эквивалентная схема нелинейного элемента выполнена в виде перекрытого Т-образного че-

а

б

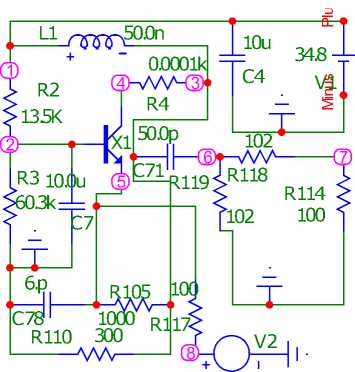
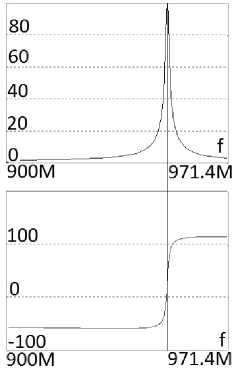
Рис. 5. Принципиальная схема однокаскадного усилителя ( а ), соответствующая структурной схеме (рис. 1, а ), при напряжении U = 34,8 В, АЧХ и ФЧХ ( б ), исследуемые в системе MicroCap

Fig. 5. Schematic diagram of a single-stage amplifier ( a ), corresponding to the block diagram (Fig. 1, a ), at voltage U = 34,8 V, frequency response and phase response ( b ), studied in the MicroCap system

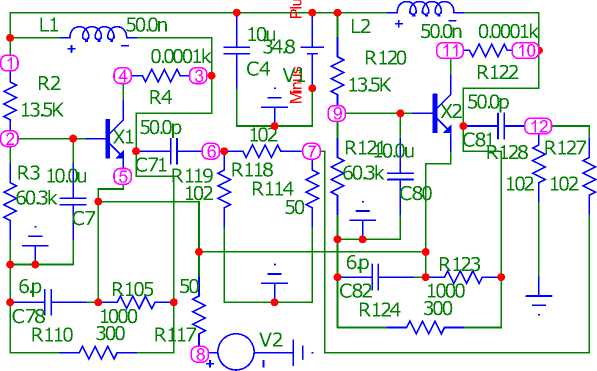
Рис. 6. Принципиальная схема двухкаскадного усилителя с одинаковыми каскадами, соответствующая структурной схеме (рис. 1, а ), частотные характеристики (рис. 5, б ) которого идентичны соответствующим характеристикам (рис. 5, б ) однокаскадного усилителя (рис. 5, а )

Fig. 6. Schematic diagram of a two-stage amplifier with identical stages, corresponding to the block diagram (Fig. 1, a ), the frequency characteristics (Fig. 5, b ) of which are identical to the corresponding characteristics (Fig. 5, b ) of a single-stage amplifier (Fig. 5, a )

тырехполюсника на элементах R_w, L 6 , R 13 , L 7 , R 11 , L 9 , R 9 , L 5 (рис. 7). Параметры эквивалентной схемы НЭ выбраны из условия совпадения выходного сопротивления НЧ с выходным сопротивлением НЧ с использованием реального транзистора [9].

Частотные характеристики принципиальных схем, показанные на рис. 5, б (сопротивления источника сигнала и нагрузки равны 100 Ом) и 6 (сопротивления источника сигнала и нагрузки равны 50 Ом), идентичны. Это соответствует выводам, сделанным на основе анализа полученных ранее [1; 3] выражений для передаточных функций исследуемых многокаскадных структурных схем (рис. 1, а).

Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов - С 8 , R 19 , R 22 . Параметры ЦОС заданы произвольно. Схема РЧ собрана на основе Г-образного соединения двух элементов ^- R 23 , R 24 .

Таким образом, при использовании РЧ также наблюдается новое явление, состоящее в том, что при определенных соотношениях между количеством каскадов и значениями сопротивлений

O.^6B5J5n     R10

—,-■,..-,.,-,,-,.--^м-

LB 4.891112

-78.073П 5     R23

*

T9 2.073065г

< R13 < 25.957347

f L7

< 6.513337г

6.0p C8 300 R22

|—II------VA--

,F19jW 000----

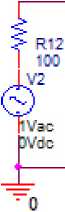
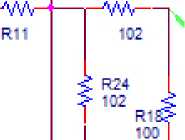
Рис. 7. Эквивалентная схема однокаскадного усилителя (рис. 5, а ), соответствующая структурной схеме (рис. 1, а ), исследуемая в системе OrCad

Fig. 7. Equivalent circuit of a single-stage amplifier (Fig. 5, a ), corresponding to the structural diagram (Fig. 1, a ), studied in the OrCad system

а

б

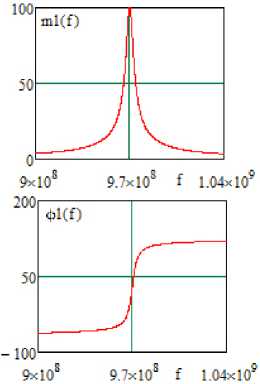
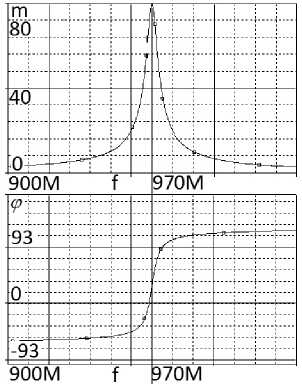
Рис. 8. Частотные характеристики (АЧХ и ФЧХ) эквивалентной схемы (рис. 7), полученные в системе MathCad ( а ) и OrCad ( б )

Fig. 8. Frequency characteristics (frequency response and phase response) of the equivalent circuit (Fig. 7), obtained in the MathCad (a) and OrCad (b) systems источника сигнала и нагрузки однокаскадного радиоустройства частотные характеристики однокаскадного и многокаскадного радиоустройств оказываются идентичными или подобными [1]. Такие схемы названы эквивалентными.

Необходимо отметить, что это явление наблюдается при любой сложности каскадов типа «НЧ – РЧ», а также при отсутствии НЧ или РЧ. Указанное явление не зависит от структуры схемы, включенной между источником сигнала и нагрузкой, и значений параметров этой схемы.

Анализ также показывает, что экспериментальные (рис. 5, б) частотные характеристики принципиальной схемы усилителя (рис. 5, а, 6) удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 7) усилителя, получен- ными расчетным путем (рис. 8, а) и экспериментально (рис. 8, б).

Средняя частота эквивалентной схемы f ® ® 970 МГц (рис. 8, а и б) незначительно отличается от средней частоты принципиальной схемы f ® 971,4 МГц (рис. 5, б ). Значения модулей передаточной функции принципиальной и эквивалентной схем усилителя m = 100. Сопротивления РЧ, ЦОС, нагрузки и источника сигнала принципиальных и эквивалентных схем АФМ полностью совпадают.

При использовании неодинаковых каскадов возникает возможность значительно увеличить рабочую полосу частот. Например, для двухкаскадной схемы (рис. 9) произведение коэффициента усиления на полосу частот составляет при-

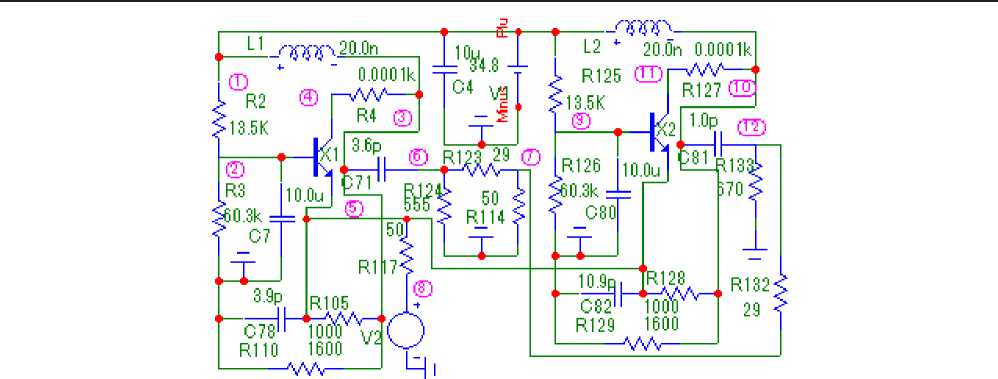
Рис. 9. Принципиальная схема двухкаскадного усилителя с неодинаковыми каскадами, соответствующая структурной схеме (рис. 1, а ), частотные характеристики которого, полученные в системе MicroCap, показаны на рис. 11, а

Fig. 9. Schematic diagram of a two-stage amplifier with unequal stages, corresponding to the block diagram (Fig. 1, a ), the frequency characteristics of which, obtained in the MicroCap system, are shown in Fig. 11, a

L5 9.0n

125.873025p R10

!.012016p R31 -3.3+898

125.873025p R27

'--II--VA-

CH -22.443+84

8.012016^11 R13 ■3 34898

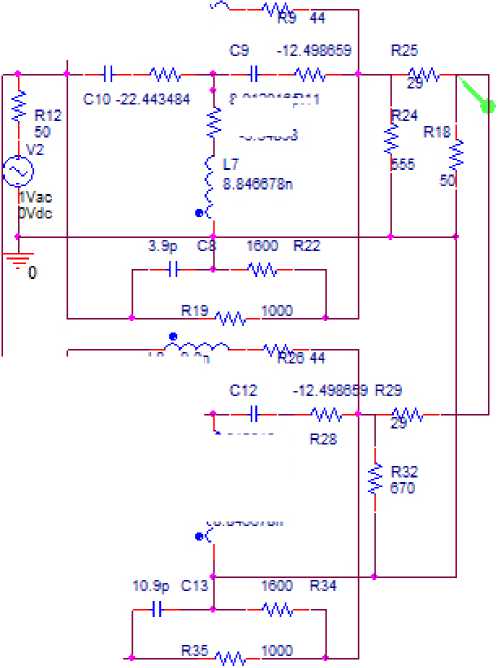
Рис. 10. Эквивалентная схема двухкаскадного усилителя (рис. 9) с неодинаковыми каскадами, соответствующая структурной схеме (рис. 1, а ), исследуемая в системе OrCad

Fig. 10. Equivalent circuit of a two-stage amplifier (Fig. 9) with unequal stages, corresponding to the block diagram (Fig. 1, a ), studied in the OrCad system

L8 9.

< L9 <8.84667811

мерно 450 (рис. 11). Это почти в 3 раз больше, чем произведение коэффициента усиления на полосу частот однокаскадного усилителя или двухкаскадного усилителя с одинаковыми каскадами.

Средняя частота эквивалентной схемы (рис. 10) f ® 735 МГц (рис. 11, б и в) незначительно отлича- ется от средней частоты принципиальной схемы f ® 734 МГц (рис. 11, а). Значения модулей передаточной функции принципиальной (рис. 10) и эквивалентной (рис. 11) схем усилителя m = 100. Формы АЧХ и ФЧХ совпадают удовлетворительно. Сопротивления РЧ, ЦОС, нагрузки и источ-

а

б

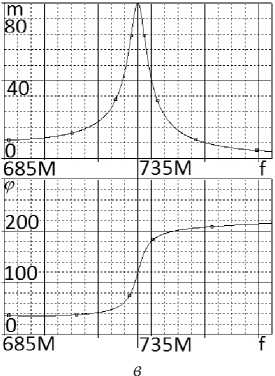
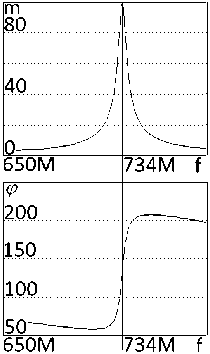
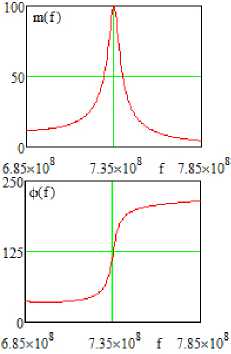
Рис. 11. Частотные характеристики (АЧХ и ФЧХ) принципиальной (рис. 9) эквивалентной (рис. 10) схем, полученные в системе MicroCap ( а ), MathCad ( б ) и OrCad ( в )

Fig. 11. Frequency characteristics (frequency response and phase response) of the principal (Fig. 9) equivalent (Fig. 10) circuits obtained in the MicroCap (a), MathCad (b) and OrCad (c) system ника сигнала принципиальных и эквивалентных схем усилителей полностью совпадают.

В работе [12] показано, что результаты схемотехнического моделирования удовлетворительно совпадают с результатами экспериментальных исследований физических макетов радиоустройств.

Заключение

Таким образом, полученные математические модели РЧ типа (1)–(14) могут быть использованы для технического проектирования радиоустройств с одинаковыми каскадами. Возможность изменения величины эквивалентного сопротивления источника сигнала и нагрузки путем включения произвольного количества каскадов типа «НЧ – РЧ» значительно упрощает решение многих задач радиоэлектроники [13], например задач обеспечения однонаправленности распространения сигнала и независимости процессов, происходящих в предыдущем и последующем динамических звеньях систем автоматического регулирования. Использование полученных математических моделей одного из РЧ (15)–(28) совместно с известными численными методами позволяет ускорить процесс оптимизации радиоустройств с неодинаковыми каскадами по критерию обеспечения максимально возможной рабочей полосы частот в десятки и сотни раз по сравнению с применением только численных методов.