Параметрический синтез различных радиоустройств с заданным количеством каскадов типа «нелинейная часть - смешанный четырехполюсник»

В работе [1] предложены алгоритмы параметрического синтеза плоско-слоистых сред (ПСС), содержащих заданное количество управляемых и неуправляемых слоев, по критерию обеспечения заданной амплитудно-фазовой модуляции рассеянного сигнала. Управляемые слои – это двумерно-периодические решетки проводящих стержней или полосок, в разрывы которых включены нелинейные элементы, управляемые низкочастотным сигналом. Неуправляемые слои (НС) – это однородные диэлектрические слои без потерь или двумерно-периодические решетки стержней или полосок. В общем случае ПСС функционирует в смешанном режиме – присутствует как отраженная, так и проходная волна. Если один из НС, расположенный последним по

направлению падающей волны, выполнен в виде проводящего экрана, то ПСС является отражающей. В этом случае ПСС может быть использована в качестве основы для построения перспективной курсо-глиссадной системы [2]. Суть алгоритмов состоит в формировании систем алгебраических уравнений, отвечающих требованиям к системным операторам (коэффициентам отражения и передаточным функциям) в заданном количестве состояний, удовлетворяющих заданным уровням низкочастотного сигнала. Результатом решения этих уравнений является система взаимосвязей между элементами классической матрицы передачи некоторых НС, отнесенных к неуправляемой части. Оставшаяся часть НС отнесена к управляемой части ПСС. Система взаимосвязей – это ис-

ЕЭЕ^Ж © Головков А.А., 2024

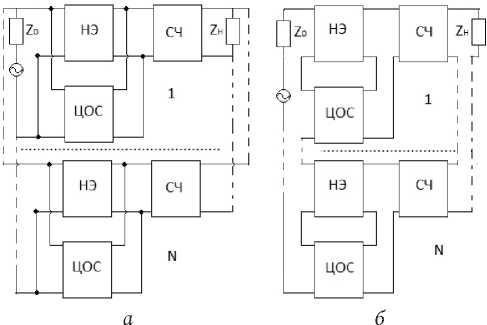
Рис. 1. Структурные схемы многокаскадных радиоустройств с параллельной по напряжению ( а ) и последовательной по току ( б ) ЦОС, включенными между источником сигнала и СЧ Fig. 1. Structural diagrams of multi-stage radio devices with parallel voltage ( a ) and serial current ( b ) digital signal processing systems connected between the signal source and the midrange

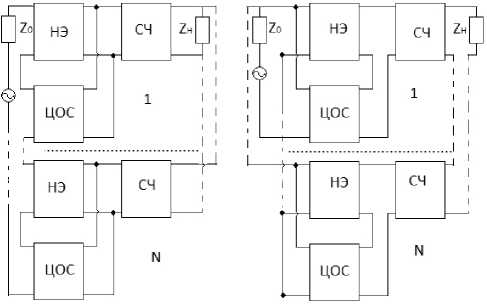
Рис. 2. Структурные схемы многокаскадных радиоустройств с последовательной по напряжению ( а ) и параллельной по току ( б ) цепями обратной связи, включенными между источником сигнала и СЧ

Fig. 2. Structural diagrams of multi-stage radio devices with serial voltage ( a ) and parallel current ( b ) feedback circuits connected between the signal source and the midrange

ходная система уравнений для отыскания параметров НС.

Разработанные алгоритмы могут быть использованы практически в любом диапазоне радиочастот. Отличие состоит лишь в реализации элементов классической матрицы передачи НС. В соответствующих диапазонах частот это могут быть элементы либо с распределенными параметрами [1; 2], либо с сосредоточенными параметрами [3–7]. Для реализации геометрических размеров неуправляемых и управляемых решеток ПСС [1; 2] необходимо привлечение результатов решения задач дифракции электромагнитных волн на различных проводящих телах [8].

Наиболее полно метод решения задач параметрического синтеза различных радиоустройств (за исключением многокаскадных) с обоими типами элементов изложен в работе [9].

В данной работе предлагается рассмотреть особенности этих алгоритмов с учетом наличия каскадов типа «нелинейная часть (НЧ) – смешанный четырехполюсник (СЧ)».

Эти каскады включены между источником сигнала с сопротивлением z о = i^ + jx о и нагрузкой z_^ = r_^ + jx_^ (рис. 1, 2). При этом учитывалось, что НЧ состоит из трехполюсного нелинейного элемента (НЭ) и охватывающей его цепи обратной связи (ЦОС – параллельной или последовательной по току или напряжению).

Оптимизация параметров двухполюсников, не входящих в КЧ, осуществляется с помощью известных численных методов [10] по критерию обеспечения заданной рабочей полосы частот. Все обозначения неописанных величин в данной статье соответствуют принятым в [9].

Алгоритм синтеза многокаскадных радиоустройств с учетом наличия каскадов типа «РЧ – НЧ» приведен в работе [11].

1. Результаты параметрического синтеза

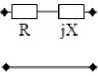
Здесь в качестве примера приводятся некоторые из решений, полученных для типовых схем СЧ при использовании параллельной по напряжению обратной связи (рис. 1, а ). Если синтезируется радиоустройство с одинаковыми каскадами [11], а в качестве СЧ используется последовательное соединение сопротивлений R и X (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом (аргументы опущены):

⁽ 1 - ^d r - e r )b_r - b x ^{( d} x ⁺ e x ) R =-------------------

b r + b x

X = ( d_r + e r - 1) b x - b_r ( d_x + e x ) ■         b r + b x

;

.

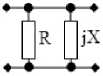
Два параллельно соединенных сопротивления R и X (рис. 3, б ):

R =

^c r ²

+ c

2 x

(1 - d - e )c - c (d + e ) r r r xx x

X =

:² + c ² rx

^{( d}x ⁺ ex ^)cr - cx ^{( d +} e ^- 1) x x r xr r

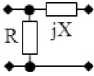
Г-образное соединение двух сопротивлений R и X (рис. 3, в ):

^Xd x ^- c r d_r + e_r - 1 - Xb_x

а

Рис. 3. Синтезированные СЧ

Fig. 3. Synthesized mixed quadrupole

б

в

абв

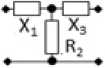
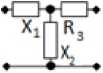
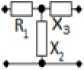
Рис. 4. Синтезированные СЧ (продолжение)

Fig. 4. Synthesized mixed quadripoles (continued)

_v_ - B 2 ± ] B - 4 A 2 C 2 X

2 A ₂

где

в

аб

A 2 — b r d x - b x d r ;

Bn — d² + d 2 + d_re_r + d_xe_x - d_r - b_rc_r - b_xc_x ;

r x rr xx r rr xx

C ^— ( d + e ^- 1) c ^- c ( d + e ). r r x rx x

Рис. 5. Синтезированные СЧ (продолжение)

Fig. 5. Synthesized mixed quadripoles (continued)

Г-образное соединение двух сопротивлений X

и R (рис. 4, а ):

R _— X ^{( d} x + e x ) - ^cr . d r - Xbx    ’

_{X —} ⁽ d r ⁺ e r ^{- 1 - X} 3 b r ) R 2 ^{+ c} r ^{- X} 3 d x

¹              R 2 b x + ^X 3 ^b r

„ _ - B 2 ± ]B 2 - 4 A 2 C 2

Rn —--------------------- ,

²           2 A ₂

где

- B_o ± _xIB: X — —²—^

'2

2 A ₂

4 A ₂ C ₂

,

где

A ₂ — ( d + e ) b - b (d + e - 1); x xr x r r

^A 2 ^{— (} d r ⁺ e r ^{- 1 ) b} r ⁺ b x ⁽ d x ⁺ e x );

^B 2 ^{— (} b 2 ⁺ b 2 ) ^X 3 ⁺ [² bx ⁺ brex ^- bxer ^{] X} 3 ⁺ r x        x rx xr

+ 1 - d r - e r + b r c r + b x c x ;

Cn — ( bd + bd ) X 2 + ( d_x + bc - hc_r ) Xn - c_r . r r x x        x rx xr       r

2 r x rr xx

-

d r ^- b r c r ^- b x ^c x ;

C 2 — c x d r - c r d x .

Обратное Г-образное соединение двух тивлений R и X (рис. 4, б ):

_R^cr ^- X ^{( d} x ⁺ e x )

R —                 ;

Xb x + 1

( d + e - 1 - Xnb ) Rn + c - Xnd rr      r r x

R 2 ^b x + ^X 3 ^b r

сопро-

- B 2 ± № - 4 A 2 C 2

X ^—       2 A      ,

где

A ^{— (} dr ⁺ er ^- ^bx ^- br ⁽ dx ⁺ ex ^); r r x rx x

Bn — d_r + e_r - 1 + b_rc_r + b_xc_x ; Cn — c_x . r r rr xx        x

Обратное Г-образное соединение тивлений X и R (рис. 4, в):

двух

сопро-

c

R —----- r—

Xb x + 1 - d r

-

^; e_r

- ^B 3 ± B ^B 3 - ^{4 A} 3 ^C 3

2 A ₃

где

A ₃ — ( b ^! + b 2² ) R ₂ + b_rd_r + b_xd_x ; r x rr xx

Bn — d_x + b_rc_x - b_xc_r + Rn (2 b_x + b_re_x - b_xe_r ); x rx xr      x rx xr

^C 3 ^{— [( d}r ⁺ er ^{- 1} br ⁺ bx ^{( d}x ⁺ ex ^{)] R 2 +} r r r xx x

^{+ ( b}r^cr ^{+ b} x ^c x ^{+ 1 - d} r ^- e r ) ^R 2 ^{- c} r .

_{R —}    ^{( d} x ^{+ X} 1 ^b r ) ^X 3 - ^c r   .

²    d r + e r - 1 - b x ( X 1 + X 3 )

_v _ - ^B 3 ± ]^B 3 - ^{4 A} 3 ^C 3

X ^{3 —}        2 A 3        ’

_v_ - B 2 ± J B2 - 4 A 2 C 2 X

2 A ₂

где

-An — — b \ Bn — d н^- e — 1 f b c ~\~ b c 1

2 x ^;    2 r r r r x x ^;

^{C — (} dx ⁺ ex)^{c - c}x ^{( d +} e ^- 1). x xr x r r

Т-образное соединение трех сопротивлений

X ₁₃ и R ₂ (рис. 5, а ):

где

An — bd -bd -X(br2 + b2); xr xrr x

B3 — [bx (2dr + er - 2) - br (2dx + ex)]X + xr rrx x

+ d_r - d² - d² + bc_r + b_xc_x - d_re_r - d_xe_x ; r r x rr xx rr xx

Cn — (dr + er -1 + bc + bc ) X - b X2 + r r rr xxx

^{+ ( d}x ⁺ ex ) ^cr ^{- c}x ^{( d}r ⁺ e ^- 1). x xr x r r

Т-образное соединение трех сопротивлений

X ₁₂ и R ₃ (рис. 5, б ):

аб

в

Рис. 6. Синтезированные СЧ (продолжение)

Fig. 6. Synthesized mixed quadripoles (continued)

где

A = ^{( b} 2 ^{- b} 2 ) ^X 3 ^{+ ( d}r ⁺ er ^{- 1Ь}х ⁺ br ( ^dx ⁺ ex ^);

r x        r r x rx x

B2 = (b2 - b2 )X3 + [(2dr + er - 2)bx + br(2dx + ex)]X3 + r x    rr xrxx

+ d r + e r - 1 - b r c r + b x c x ;

X = R3 dr + cr - X2 (dx + ex + R3 bx) 1           R 3 bx + X2 br v _ - B2 ± J B22 — 4 A 2 C 2

x? = ,

²          2 A ₂

где

C ² = ( b_rd_x + b d ) X 2 + ( d - b c + b c ) X ₃ + c . r x x r        r rr xx       x

_   X3dx + X2 (dx + ex + X3br) - cr x     xx r r

^R 1 =           L            \ Л          ^;

A = ⁽ b2 ⁺ b ² ) R 3 ^{+ (} dr ⁺ er - 1 ) br ⁺ bx ( dx ⁺ ex ^); r x       r r r xx x

By = d_Y + e_Y - R o ( b_re_Y - b_Ye_r ) + b_rc_Y - b_Yc_r ;

x x     rx xr   rxxr

C2 = (bd + bd )R2 + (b c - d + b c )Ro - rrxx   rrrxx r

R3dr + cr - X2(dx + ex + R3bx) rrxx x

-X;

^{1            R} 3 b x + X 2 b r

R 3 =

- ^B 3 ± B 2 3 - ⁴ A 3 ^C 3

2 A ₃

где

^A 3 = b r d r ⁺ b x d x ;

B 3 = ( b2 + b 2 ) X ² + ( b_xe_r - br^ex ) X 2 - d_r + b_rc_r + b_xc_x ; r x       xr rx      r rr xx

C3 = [(dr + er - 1) br + bx(dx + ex)] X2 + r r r xx x

^{+ (} d x ⁺ e x ⁺ brcx ^- b x c r ) X 2 ^- c r .

X =   ⁽ d r ^- X 1 b x ) ^R 3 ⁺ c r _;

^ d + e + R₃b_x + X^b xx x r

- ^B 3 ± B 2 3 - ⁴ A 3 ^C 3

2 A ₃

где

A 3 = ^br^dr ^{+ b} x ^d x ;

B 3 = d r - d_r + d x +

⁺ [ ^{( 2 d} _x ^{+ e} _x ) ^b _r ^{- b} _x ^{( 2 d} _r ^{+ e} _r ^)] X ⁺ X 2 ^{( b} 2 ^{+ b} 2 ) ⁺ x xr x r r           r x

+ bc_r + b_Yc_Y + d_re_r + d_Ye_Y ; rr xx rr xx

^C3 = ⁽ d r ⁺ e r ^{- 1} c r ⁺ c x ^{( d} x ⁺ e x ) ⁺

^{+ (} b r c x - b x c r - ^d x - e x ) X 1 ^{- b}r^X 2 .

v _ - B 3 ± BB 3 2 - 4 A 3 C 3
3            2 A 3         , где A 3 = bd + bd + ( br 2 - b 2 ) X 2 ; rx   xr   r   x B 3 = ( b r - b 2 ) X 2 + dr - brcr + bx r    x        r   rr	: cx +
+ X 2 [(2 dr + er - 2)bx + br (2 dx + ex )]; rr xrxx
C 3 = cx + [( d + e - 1 ) b + b ( d x    r r    x rx	+ e x )] X 2 +
+ ( d + e - 1 - b c + b c ) X 2. r r      rr xx
r 13 x 1 x -X q                                     ;	(15)
d x + e x + R 1 b x + X 3 b r
v _ - B 3 ± j B 3 - 4 A 3 C 3
3            2 A 3         ,
где
A = bd + bd + ( br 2 + b 2 ) R ; rr xx   r x
B o = d „ + bc - bc + de - d„	e „ +
3    x rx xr rx x
+ (2 b + b e - b e ) R ; x rx xr
C 3 = ( d + e - 1) c + c ( d + e ) r r    r xx x	- R 2 br +
+ ( bc + bxcx - d - e + 1) R . rr xx r r
П-образное соединение	трех сопротивлений
X 13 и R 2 (рис. 6, а ):
v     ( cr - X3dx ) Ry - X3cx rx   x	;                           (16)
( d + e - 1 + Ryb ) X 3 + c rr     r    x

—

R 2 =

- B ₂ ± BB:

где

2 A ₂

4 A ₂ C ₂

,

Т-образное соединение трех сопротивлений

X ₂₃ и R ₁ (рис. 5, в ):

^X3^dx ⁺ X ^{2 ( d}x ⁺ ex ^{+ X}3^br ) ^- cr x     xx r r

Ri =-----------------------------

^{1           b} x ( X 2 + X 3 ) + ¹

A = ( b d + b d ) X 2 + ( d + b c - b c ) X ₃ - c ; r r x x        x rx xr       r

By = ( b c + b c - d + d e + d e ) X 2 + rr xx r rr xx

^{+ (} cxer ^- crex ) ^X 3 ^{+ ( c}x ^{+ X}3^dr ^{)2 + (} cr ^{- X}3^dx ^)2; xr rx       x r     r x

C = ^[( dr ⁺ er ^- 1) cr ⁺ cx ^{( d}x ⁺ ex ^{)] X} 3 . r r r xx x

X ₂ =

- B 2 ±

] B 2 - 4 A 2 C 2

2 A ₂

( c _r - X₃d_x ) Ry - X₃c_x rx   x

( d + e - 1 + Ryb ) X ₃ + c rr     r    x

_y _ - B 3 ± 7 B 3 - ⁴ A 3 C 3

X3 =      2A3       , где

A = (d2 + d2 — dr + brcr + bc + d e + d e )R2 + r x r rr xx rr xx

⁺ ( ^d r + e r - 1 ^)c r + c x ( ^d x + e x ) + R 2 ( b r ^d r + b x ^d x ^);

B 3 = ^{( d}x ⁺ brcx - bxcr ) R ^{2 -} x rx xr

^- R [ ^{( 2 d} _x + e_x ) c_r - c_x ⁽ 2 d + e )]; x xr x r r

C 3 = R 2⁽ c r ⁺ c x ) - ^{R 2} c r •

R = (i-dr—erXX^zCx^^.

2          (dx + X 1 br) X3 - cr’ y _ - B3 ± ] B 3 - 4 A 3 C 3

X3 =      2A, где

A 3 = cx^{d - c}r^dx ^- bxerX ^{2 + [( d}x ⁺ X l b r^{)( d}x ⁺ ex ) ⁺ x r r x xr         x r x x

^{+ d}rer ^{+ ( d}r ^{- 1 )( d}r ^- Xbx ) ^- brcr ^- bxcx ^] X I^; rr r r x rr xx

B 3 = ⁽ X 1 ^- cx ^{)2 +} cr ^- X ^{2 ( d}r ⁺ er ⁺ brcr ⁺ bxcx ) ^-

^- X ^{[( 2 d + e} ) ^{c - c ( 2 d + e )];} x xr x r r

C 3 = X 1⁽ c r ⁺ c x ) ^- X ² c x •

П-образное соединение трех сопротивлений X ₁₂ и R ₃ (рис. 6, б ):

( c_r - X₂d_x ) R o - X₂c_x

X, = ------ ^r -----^{2 x 3}----- ² x ;                      (19)

( d_x + ex + X^br ) R 3 + Cx - X xx r x

_v _ - B 2 ± JB 2 - 4 A 2 C 2

X? =----------------

²          2 A ₂

где

A ₂ = ( b d + bd ) R 2 - c + R ₃ ( bc - d + bc ); rrxx r rrrxx

B2 = (d + brcx - bxc + x rx xr

^{+ d} r e x ^{- d} x e r ) ^R 3 ^{+ (} c r e x ^- c x e r ) ^R 3 ;

C 2 = ^R 3^{( C} X ⁺ c ² ) ^{+ R} 3 ^{[( d} r ⁺ e r ^- 1) c r ⁺ c x ^{( d} x ⁺ e x ^)] .

( c _r - X₂d _x) R ₃ - X₂c_x rx   x

¹   ( d + e + X₂b ) R ₃ + c_x - X₂

xx r x

„ _ - B 3 ± ] B 3 - ⁴ A 3 C 3

Ro =, где

A ₃ = ( d_x + bc_x - b_xc_r + d_re_x - d_xe_r ) X ₂ + x rx xr rx xr

+ (b d + b d )X2 + c (d + e -1) + c (d + e ); rr xx       r r rx x x

B 3 = ^X 2⁽ crex ^- cxer ) ⁺ c ^{2 +} c ^{2 + X} 2 ⁽ brcr ^{- d}r ⁺ bxcx ^);

rx xr r x      rr r xx

C 3 =

^X 2 c r •

[cr - X(dx + ex)]R3 rxx

.X n —

^{( d} _x ^{+ X} 1 ^b _r ) ^R 3 ^{+ c} _x

-

X ₁ c_x

X 1 ;

-

„ _ - B 3 ± J B 3 - ⁴ A 3 C 3

R3= где

A 3 = c d + c d + X 2 [( d + e - 1) b + b ( d + e )] - rr xx        r r r x x x

- X ( d - b_rc_x + b_xc + d e - d e ); x rx xr rx xr

B 3 = ^{X 2 (} brcr ⁺ bxcx ^{+ 1 - d}r ^{- e}r ) ^{+ c 2 + c 2 -} rr xx r r r x

—   (2c + c e — ce):

г x r x x r ^;

C 3 = ^{- X} 1 ^c r •

П-образное соединение трех сопротивлений R ₁

и X ₂₃ (рис. 6, в ):

( c _x + Xod_r ) X ₂ + X o c_x

R = -^---3 r—2---3-x ;(22)

cr - X3(dx + ex + X2br) rxx r v _ - B2 ± ^ B2 - 4 A 2 C 2

X? =---------------- где

A = (b d - b d ) X2 + (d + b c + b c ) X3 + c ; x r r x        r rr xxx

B 2 = ⁽ b r c r ⁺ b x c x ^{+ d} r ^{- d} r e r ^{- d} x e x ) ^X 3 ⁺

+ ⁽ 2 c + ce ^- c e ) X ^{- (} c + X^^d_r ^{)2 - (} c_r ^{- X}^^d_x ^)2;

x rx xr        x r r x

C2 = X3[(dx + ex)cr - cx(dr + er -1)] - X3(cг + c2

x xr x r rr x n    (cx + X3dr) X2 + X3cx xrx

R. =  ;

^c r ^{- X} 3^{( d} x ⁺ e x ^{+ X} 2 ^b r )

_y _ - B 3 ± JB 3 - ⁴ A 3 C 3

Xo =, где

A 3 = ^cr ^{( d}x ^{+ e}x ) ^{- c}x ^{( d}r ⁺ er ^- 1) ^{- X} 2 ^{( b}r^dx ^{- b}x^dr ) ^- r x x x r r           rx xr

- X ₂ ( d 2 + d ² - d - b c - b c + d e + d e ); r x r rr xx rr xx

B 3 = ^X 2 ^{[( 2 - e}r ^{- 2 d}r ) ^cx ⁺ cr ^{( 2 d}x ⁺ ex ^{)] - c} г ^{- c 2 +} r rx r x x r x

^{+ X} 2 ^{( d} x ⁺ b r c r ⁺ b x c x );

C 3 = ^X 2 ^c x ^{- X} 2^{( c} r ^{+ c} x )•

^{[ c}r ^{- X} 3^{( d}x ⁺ ex ^)] R ^{2 - X}3^cx r    xx      x

• ^{2        ( d} _r ^{+ R} 1 ^b _r ) ^X 3 ^{+ c} _x

_y _ - B 3 ± ] B 3 - ⁴ A 3 C 3

X3=       2A3        ’ где

A 3 = ^{[( d}r ⁺ R²b r^{)( d}r ^{+ e}r ^- 1) ^{+ ( d}x ⁺ Rbx ^{)( d}x ⁺ ex ) ⁺ r rr r     x xx x

+ b_rc_r + b_xc_x ] R + c_rd_r + c_xd_x ; rr xx r r x x

B3 = R ^{2 ( d}x ^{+ e}x ⁺ brcx ^- bxcr ) ^- x x rx xr

^- R ^[( 2 d + e ^{) c -} c ⁽ 2 d + e ^)]; x xr x r r

C 3 = ^R 1 ( c 2 + c x ²) - ^R 1² c r •

Если синтезируется радиоустройство с неодинаковыми каскадами [11], а в качестве СЧ ис-

пользуется последовательное соединение сопротивлений R и X (рис. 3, а ), то зависимости этих сопротивлений от частоты определяются следующим образом:

X = R 2 C d ^{+ C} 2 r   X 3^{( d} 1 x ⁺ R 2 ^b x ) .

1        R 2 ^b x ^{- d} x ⁺ X 3 ^b r

„   - B 2 ± V B 2² - 4 A 2 C 2

R? =----------------

²           2 A ₂

где

R   C.b'-b.D . X Cdb-bD b2 + bx2 ’         ь2 + ьХ    , где

C d = ^C r ^{- C} 1 r ^- d r ^{+ d} 1 r ^; D C = ^C x ^{- c} 1 x ^- d x ^{+ d} 1 x •

Два параллельно соединенных сопротивления

R и X (рис. 3, б ):

R = ^C 2 ^{r + C} 2 ^x ; X = ^C 2 ^{r + C} 2 ^x .            (26)

C d ^C 2 r ^{+ C} 2 x ^D C        ^D C ^C 2 r ^{- C} 2 x C d

• ^B 2 = ^b r ^C 2r ^{+ b} x ^C 2x ^{+ ( C} 1 r ^{- C} r ^{- d} 1 r ) ^d r ^-

• - dx(Cx - C1 x + d1 x)+ (dx - brX3)2 + (dr + bxX3)2 +

⁺ X 3 К ^C 1 r ^{- C} r ) ^b x ^{+ b} r ^{( C} x ^{- C} 1 x ^)];

• A 2 = ^b r C d + ^b x D ;

C 2 = ^{( b} r ^d 1 r ^{+ b} x ^d 1 x ) X 3 ⁺

• ^{+ ( b} r ^C 2 x ^{- b} x ^C 2 r ^{+ d} r ^d 1 x ^{- d} x ^d 1 r ) X 3 ^{- C} 2 r ^d r ^{- C} 2 x ^d x •

Г-образное соединение двух сопротивлений R и

X (рис. 3, в ):

_R = C 2 r - Xd 1 Х . X = - B 2 ± B* 2 - ⁴ A 2 C 2

^Xb x - Cd ’             ² A 2

где

^B 2 = ^d 1 r C d ^{+ d} 1 x ^D C ^{- b} r ^C 2r ^{- b} x ^C 2x ^;

A 2 = ^b r ^d 1 x ^{- b} x ^d 1 r ^; C 2 = C d ^C 2 x ^{- C} 2 r ^D C •

Г-образное соединение двух сопротивлений X

и R (рис. 4, а ):

R = XDc - C^ , X = - ^B 2 ± B^B 2 - ⁴ A 2 C 2 d i r - Xbx ’              2 A 2

X = R 2 C d ^{+ C} 2 r   X 3^{( d} 1 x ⁺ R 2 ^b x ) .

1       R2 bx - dx + X3 br y _ - B3 ± 7 B3 -4 A 3 C 3

X3 =      2A      ’ где

^B 3 = [ ^C 2 x ^- R 2^{( C} 1 x ^{- C} x ^{+ 2 d} x ^{)] b} r ^-

^{- b} x [ ^C 2 r ^{- R} 2^{( C} 1 r ^{- C} r ^{+ 2 d} r ^{)] + d} r ^d 1 x ^{- d} x ^d 1 r ^;

A 3 = R 2 ( b r + b x ) + ^b r ^d 1 r + ^b x ^d 1 x ;

C 3 = [ C 0 ^{- ( d} x ^{- R} 2 ^b x ) ^D C ^{] R} 2 ^{- ( C} 2 r ^d r ^{+ C} 2 x ^d x ^);

C 0 = ^{( b}r^C 2r ^{+ b} x ^C 2 x ^{+ ( d} r ^{- R} 2 ^b r ^)Cd •

где

^B 2 = ^b r ^C 2r ^{+ b} x ^C 2x ^- C d ^d 1 r ^{- D} C ^d 1 x ^;

A 2 = ^b x C d ^{- b} r ^D C ^; C 2 = ^C 2 r ^d 1 x ^{- C} 2 x ^d 1 r •

Обратное Г-образное соединение двух сопро-

тивлений R и X (рис. 4, б ):

R = .^ XD  X = - B 2 ± BB 2 - ⁴ A 2 C 2

d_r + Xbx ’              2 A ₂        ’

где

^B 2 = ^{- ( b} r ^C 2 r ^{+ b} x ^C 2 x ⁺ C d ^d r ^{+ D} C ^d x );

A 2 = ^b r ^D C ^{- b} x C d ^; C 2 = ^C 2 r ^d x ^{- C} 2 x ^d r •

Обратное Г-образное соединение двух сопро-

r = ^C 2 r ⁺ X 1 ^d x X 3^{( d} 1 x ⁺ X 1 ^b r ) .

2       (X1 + X3) bx ~ Cd v _ -B3 ± ]B3 - 4 A 3 C 3

X3=     2A     ’ где

A 3 = X 1^{( b} r ^{+ b} X ) ^{+ b} r ^d 1 x ^{- b} x ^d 1 r ^;

B 3 = X 1 [ ^{( C} x ^{- C} 1 x ) ^b r ^{- b} x ^{( C} r ^{- C} 1 r ) ^-

^{- 2 ( b} r ^d x ^{- b} x ^d r ^{)] - b} r ^C 2 r ^{- b} x ^C 2 x ⁺

^{+ ( C} r ^{- C} 1 r ^{- d} r ) ^d 1 r ^{- d} 1 x ^{( C} 1 x ^{- C} x ^{+ d} x ^{)] +}

^{+ ( d} 1 _x ^{+ b} _r ^x 1^{)2 + ( d} 1 _r ^{- b} _x ^X 1^)2;

C 3 = C d ^{( C} 2 x ^{- x} 1 ^d r ) ^{- x} 1^{( b}r^C 2r ^{+ b} x ^C 2 x ) ^-

тивлений X и R (рис. 4, в ):

C 2 r + Xd x . X = - ^B 2 ± № - ⁴ A 2 C 2

^Xb x - C d ’             ² A 2

^{- x 2 ( b}r^d_X ^{- b}_X^dr ) ^{+ ( C}2r ⁺ Xdx ) ^Dc • rx xr r x c

Т-образное соединение трех сопротивлений

X ₁₂ и R ₃ (рис. 5, б ):

X = ^C 2 r ^{+ R} 3 ^d 1 r ^- X 2^{( D} c ^{+ R} 3 ^bx ) .                  (34)

1        R3bx - dx + X2b       ’ xx r

где

^B 2 = ^b r ^C 2 r ^{+ b} x ^C 2 x ⁺ C d d r ^{+ D} C ^d x ^;

A 2 = ^b r ^d x ^{- b} x ^d r ^; C 2 = ^C 2 r ^D C ^{- C} 2 x C d •

Т-образное соединение трех сопротивлений

X ₁₃ и R ₂ (рис. 5, а ):

_v _ - B 2 ± 7 B 22 - 4 A 2 C 2 x? =----------------

²          2 A ₂

где

A = R ₃ ( b_r ² + b 2 ) + D_cb_x + b_rC_d ; r x cx r

B 2 = ( c x - c 1 x + d 1 x ) d r - d x ( c r - c l r + d 1 r ) + + brc 2 x - b x c 2 r - R 3[( c x - c 1 x ) b r - b x ( c r - c 1 r )] ; C 2 = ( b r d lr + b x d lx ) R 2 + + ( b r c 2 r + b x c 2 x - d r d lr - d x d lx ) R 3 - c 2 r d r - c 2 x d x •	v _ - B 3 ± B 2 32 - 4 A 3 C 3 X 3 _        2 A 3         , где B 3 _ b r c 2 r + b x c 2 x + d r d 1 r + d x d 1 x - ( b 2 + b x ) X 2 +
X _ c 2 r + R 3 d l r - X 2( D c + R 3 b x ) .                  (35) 1         R3bx - dx + X2b       ’                   { } xx   r	+ [ 2 ( b r d x - b x d r ) + b x ( c r - c ir + 2 dr ) - rx xr   x r    r     r - b r ( c x - c 1 x + 2 d 1 x )] X 2 ’
„ _ - B 3 ± B 2 3 - 4 A 3 C 3 R o _                       , 3          2 A 3 где	C 3 _ [ C 0 + ( d x - X 2 b r )( c x - c 1 x + d 1 x )] X 2 + + ( b r d x - b x d r ) X 2 - c 2 r d x + c 2 x d r ; A 3 _ b x d 1 r - b r d 1 x - X 2( b r + b x );
A 3 = b r d 1 r + b x d 1 x ; B 3 = ( b r + b x ) X 2 + К c 1 x - c x ) b r + b x ( c r - c 1 r )] X 2 + + b r c 2 x - b x c 2 r - d r d 1 r - d x d 1 x ; C 3 = ( C d b r + b x D c ) X 2 + ( c x - c 1 x + d 1 x ) d r - - d x ( c r - c 1 r + d 1 r ) + b r c 2x - b x c 2r ] X 2 - c 2 r d r - c 2 x d x •	22 0 r 2 r    x 2 x    r     x + ( d r + X 2 b x )( c r - c 1 r + d 1 r )• X _ c 2 r - R 1 d r - X 3( d 1 x + R 1 b x ) .                    (39) 2        D c + R 1 bx + X 3 br      ’ v   - B 3 ± B 2 32 - 4 A 3 C 3
X _ ( d x - R 3 b x ) X 1 + c 2 r + R 3 d 1 r .                    (36) 2         D c + R 3 bx + X 1 br      ’	x 3 _ , 3          2 A 3 где
p _ — B 3 ± B 2 2 — 4 A 3 C 3 R 3 =         2 A 3         , где	A 3 _ R 1 ( b r + b x 2 ) + b r d 1 r + b x d 1 x ; B 3 _ ( d 1 x + R 1 b x )( c 1 r - c r + d r ) - R 1( b r d x - b x d r ) + + b r c 2 x - b x c 2 r - ( d 1 r + R 1 br )( c 1 x - c x + d x );
A 3 = b r d 1 r + b x d 1 x ; B 3 = ( c r - c 1 r - d r ) d 1 r - d 1 x ( c 1 x - c x + d x ) + + b r c 2 r + b x c 2 x + ( d 1 x + b r X 1)2 + ( d 1 r — b x X 1)2 + + X 1 [( c x - c 1 x ) b r - b x ( c r - c 1 r )] ; C 3 = C d c 2 r + c 2 x D c - ( b r d r + b x d x ) X 2 + + [ d x ( c r — c 1 r + d 1 r ) — d r ( c x — c 1 x + d 1 x ) + + b r c 2 x - b x c 2 r ] X 1 . Т-образное соединение трех сопротивлений	C 3 _ R 1( b r c 2 r + b x c 2 x ) + ( c 2 r - R 1 d r C d + + ( С 2 x - R 1 d x ) D c - ( b r d r + b x d x ) R • П-образное соединение трех сопротивлений X 13 и R 2 (рис. 6, а ): X _ ( c 2 x + R 2 d 1 x ) X 3 - R 2 c 2 r .                    (40) 1    R 2 d x - c 2 x - ( C d + R 2 b r ) X 3 D _ - B 2 ± B* - - 4 A 2 C 2 R? _                       , 2           2 A 2
X 23 и R 1 (рис. 5, в ): r _ c 2 r - X 3 d 1 x - X 2( D c + X 3 b r ) ;                   (37) 1         ( X 2 + X 3 )h + d       ’	где A 3 _ ( b r c 2 x - b x c 2 r + d r d 1 x - d x d 1 r ) X 3 -
v _ — B 2 ± B2 22 - 4 A 2 C 2 x? _                      , 2          2 A 2	- c 2 r d r - c 2 x d x + ( b r d 1 r + b x d 1 x ) X 3 ; B 2 _ ( c 2 x + X 3 d 1 r )2 + ( c 2 r - X 3 d 1 x )2 + + X 3[( c r - С 1 r ) C 2 x - c 2 r ( c x - c 1 x )] + X 3[ b r c 2r + b x c 2x +
где A 2 _ Cdbx - brDc - X 3 ( b г + b 2 ); x rc      r x B 2 _ ( d x - X 3 b r )( c x - c 1 x + d 1 x ) + + ( d r + X 3 b x )( c r - c 1 r + d 1 r ) + b r c 2 r + b x c 2 x - - X 3( brd 1 x - b x d 1 r ) - ( d r + b x X 3)2 - ( d x - b r X 3)2 ; C 2 _ ( b x d 1 r - b r d 1 x ) X 3 + ( b r c 2 r + b x c 2 x + + d r d 1 r + d x d 1 x ) X 3 - c 2 r d x + c 2 x d r •	+ ( c r - c 1 r - d r ) d 1 r - d 1 x ( c 1 x - c x + d x )] ; C 3 _ ( c 2 r C d + c 2 x D c ) X 3 • X _ ( c 2 x + R 2 d 1 x ) X 3 - R 2 c 2 r .                    (41) 1   R 2 d x - c 2 x - ( C d + R 2 b r ) X 3 y _ - B 3 ± B 2 32 - 4 A 3 C 3 X 3 _        2 A 3         ,
r _ c 2 r - X 3 d 1 x - X 2( D c + X 3 b r ) .                  (38) 1-        ( X 2 + X 3 ) b x + dr       ’                      '	где A 3 _ ( c 2 x + R 2 d 1 x ) D c + C d ( c 2 r + R 2 d 1 r ) +

+ R 2⁽ b r c 2 r + b x c 2 X ) + ⁽ b r d lr + ^b x ^d 1X ) R 2 ^;

B 3 = R ^{2 (} b r c 2 x - ^b x c 2 r + d r d lx - d x d lr ) + + R 2^{[ 2 (} c 2 x ^d 1 r - c 2 r ^d 1 x ) + + c 2 x ⁽ c r - c 1 r ) - c 2 r ⁽ c x - c 1 x ^)] ;

C 3 = ⁽ c 2 r + c 2 x ) R 2 - R 2 ⁽ c 2 r d r + c 2 x d x ^).

= c 2 x ( X 1 + X 3 ) + X 1 X 3 C d  _;

c 2 r ⁺ X 1 d x - X 3^{( d} 1 x ⁺ X 1 ^b r )

_y _ - B 3 ± JB 3 - ⁴ A 3 C 3

X ³ =       2 A 3

где

A 3 = ^{[( d} 1 x ⁺ X 1 ^b r ) D c ^{+ ( d} 1 r ^- X 1 ^b x ^{) C}d ^- - ^b x ^c 2x ^{- b} r ^c 2r ^] X 1 ^{+ c} 2x ^d 1 r ^{- c} 2r ^d 1 x ^;

B 3 = ⁽ c 2 r ⁺ X 1 ^d x ) ^{+ (} c 2 x ^- X 1 ^d r ) ⁺

⁺ [ B 0 ^{+ (} c 2 x ^- X 1 ^d r ⁾⁽ c r ^- c 1 r ^{+ d} 1 r ) -

• -    ( c 2 r ⁺ X 1 ^d x ⁾⁽ c x ^{- c} 1 x ^{+ d} 1 x ^)] X 1 -

• ^-    X 2⁽ b_rc 2 r ^{+ b} x c 2 x ^);

B 0 = c 2 x ^d 1 r ^- c 2 r ^d 1 x ^;

C 3 = ⁽ c 2 r ^d x ^- c 2 x ^d r ) X 2 ^{+ (} c 2 r ⁺ c 2 x ) X 1

П-образное соединение трех сопротивлений

X 12 и R 3 (рис. 6, б ):

B 3 = X 2 ^{( b} r ^c 2 r ^{+ b} x ^c 2 x ^{- d} r ^d 1 r ^{- d} x ^d 1 x ) ^{+ c} 2 r ^{+ c} 2 x ^-- X 2^{[ c} 2 x ⁽ c r ^{- c} 1 r ) ^{- c} 2 r ⁽ c x ^{- c} 1 x ^)];

C 3 = ^- X 2 ^{( c} 2 r ^d r ^{+ c} 2 x ^d x ^).

=   ^{( c} 2 r   X 1 D c ) ^R 3   X 1 ^c 2 x   _;

^c 2 x ^{+ R} 3 ^d 1 x ^- X 1^{( d} r ^{- R} 3 ^b r )

„ _ - B 3 ± V B 3 - ⁴ A 3 C 3

R ³ =        2 A 3

где

A 3 = ^{[ b} r ^c 2 x ^{- b} x ^c 2 r ^{- ( d} 1 r ^- X 1 ^b x ) D c ⁺

^{+ ( d} 1 x ⁺ X 1 ^b r ^)Cd ] X 1 ⁺ c 2 r ^d 1 r ^{+ c} 2 x ^d 1 x ;

B 3 = X 1 [ ⁽ c r ^- c 1 r ^{- 2 d} r ) ^c 2 x ^- c 2 r ⁽ c x ^{+ c} 1 x ^{- 2 d} 1 x ^{)] +}

^{+ c} 2 r ^{+ c} 2 x ⁺ X 2 ^{( b} r ^c 2 r ^{+ b} x ^c 2 x C d d r ^d x D c ^);

C 3 = ^{- ( c} 2 r ^d r ^{+ c} 2 x ^d x ) X 2 •

П-образное соединение трех сопротивлений

X ₂₃ и R ₁ (рис. 6, в ):

r = ^c 2 x ⁽ X 2 ⁺ X 3 ) ⁺ X 2 X 3 ^d 1 r _;                    (46)

^{1 c} 2 r ⁺ X 2 ^d x ^{- (} D c ⁺ X 2 ^b r ) X 3

_v _ - B 2 ± В B 2 - 4 A 2 C 2

X ² =       2 A 2

где

- = ⁽ c 2 r X 2 ^d 1 x ) R 3 X 2 c 2 x _; ^{1  (} D c ⁺ X 2 ^b r ) R 3 ⁺ c 2 x ^- X 2 ^d r

X 2 =

- B 2 ± B ² 2 — 4 A 2 C 2

2 A ₂

где

A 2 = ⁽ b r c 2r ^{+ b} x c 2x ^{- d} r ^d 1 r ^{- d} x ^d 1 x ) R 3 ^-- c 2 r ^d r ^- c 2 x ^d x ^{+ ( b} r ^d 1 r ^{+ b} x ^d 1 x ) R 3 ;

B 2 = R 3^[( c x ^{- c} 1 x ^{) c} 2 r ^- c 2 x ⁽ c r ^- c 1 r ^{)] + +} R 3^[ brc 2x ^{- b} x c 2r ^{+ (} c 1 r ^- c r ⁺ d r ) ^d 1 x ^{-- d} 1 r ⁽ c 1 x ^- c x ^{+ d} x ^)] ;

C 2 = ⁽ c 2 r C d ⁺ c 2 x D c ) R 3 ^{+ (} c 2 r ⁺ c 2 x ) R 3 •

- = ⁽ c 2 r X 2 ^d 1 x ) R 3 X 2 c 2 x _; ^{1  (} D c ⁺ X 2 ^b r ) R 3 ⁺ c 2 x ^- X 2 ^d r

R 3 =

- B 3 ± B ² 3 - ⁴ A 3 C 3

2 A ₃

где

A 3 = ⁽ c 2 x ⁺ X 2 ^d 1 r ⁾⁽ c x   ^c 1 x   ^d x ) ⁺

^{+ (} c 2 r ^- X 2 ^d 1 x ⁾⁽ c 1 r ^- c r ^{+ d} r ) ⁺

⁺ X 2^{( b} r c 2 x ^- b x c 2 r ) ⁺ X 2 ^{( b} r ^d 1 r ^{+ b} x ^d 1 x ) ⁺

⁺ c 2r ^d 1 r ⁺ c 2x ^d 1 x ;

A 2 = ^{( b} r ^d 1 x   ^b x ^d 1 r ) X ^{2  ( b} r c 2 r ^{+ b} x c 2 x ⁺

^{+ d} r ^d 1 r ^{+ d} x ^d 1 x ) X 3 ⁺ c 2 r d x ^- c 2 x d r ;

B 2 = B 0 X 3 ^{+ ( c} 2 r ^- X 3 ^d 1 x ) ^{+ ( c} 2 x ⁺ X 3 ^d 1 r ) ^-

• ^-    X 3^{( b}r^c 2r ^{+ b} x ^c 2 x ^);

B 0 = ⁽ c 2 r ^- X 3 ^d 1 x ⁾⁽ c 1 x ^- c x ^{+ d} x ) ^-

• ^{-    (} c 2 x ⁺ X 3 ^d 1 r ⁾⁽ c 1 r ^- c r ⁺ d r ) ⁺ c 2 r d x ^- c 2 x d r ;

C 2 = ^{( c} 2 x C d ^{- c} 2 r D c ) X 3 ^{+ ( c} 2 r ^{+ c} 2 x ) X 3 •

„ _ ^c 2 x ⁽ X 2 ⁺ X 3 ) ⁺ X 2 X 3 ^d 1 r

R = ;

^c 2 r ⁺ X 2 ^d x ^{- (} D c ⁺ X 2 ^b r ) X 3

_v _ - B 3 ± В B 3 - ⁴ A 3 C 3

X3=      2A      ’ где

A 3 = ⁽ X 2 ^d 1 x ^{- c} 2r ^{)( c} x ^{- c} 1 x ^{- d} x ) ^-

• ^{-    (} c 2x ⁺ X 2 ^d 1 r ⁾⁽ c 1 r ^- c r ⁺ d r ) ⁺

+ X 2^{( b} r ^d 1 x ^{- b} x ^d 1 r ) ^{- c} 2 r ^d 1 x ⁺ c 2 x ^d 1 r ⁺

⁺ X 2^{( d} 2 r ^{+ d} 2 x ^{- b} r ^c 2 r ^{- b} x ^c 2 x ^);

B 3 = ^c 2 r ^{+ c} 2 x ^- X 2 ^{( b} r ^c 2 r ^{+ b} x ^c 2 x ^{+ d} r ^d 1 r ^{+ d} x ^d 1 x ) ^{+ +} X 2^{[ c} 2 x ⁽ C d ^{- d} r ^{+ d} 1 r ) ^{- c} 2 r ⁽ D c ^{- d} x ^{+ d} 1 x ^)];

C 3 = ^{( c} 2 r ^d x ^{- c} 2 x ^d r ) X 2 ^{+ ( c} 2 r ^{+ c} 2 x ) X 2 •

а

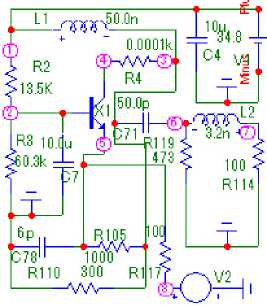
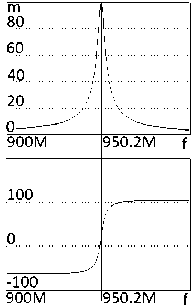
Рис. 7. Принципиальная схема однокаскадного усилителя ( а ), соответствующая структурной схеме (рис. 1, а ), при напряжении U = 34,8 В, АЧХ и ФЧХ ( б ), исследуемые в системе MicroCap Fig. 7. Schematic diagram of a single-stage amplifier ( a ), corresponding to the structural diagram (Fig. 1, a ), at a voltage of U = 34,8 V, frequency response and phase response ( b ), studied in the MicroCap system

б

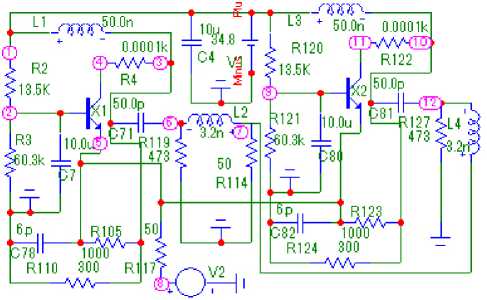
Рис. 8. Принципиальная схема двухкаскадного усилителя с одинаковыми каскадами, соответствующая структурной схеме (рис. 1, а ), частотные характеристики (рис. 7, б ) которого идентичны соответствующим характеристикам (рис. 7, б ) однокаскадного усилителя (рис. 5, а )

Fig. 8. Schematic diagram of a two-stage amplifier with identical stages, corresponding to the structural diagram (Fig. 1, a ), the frequency characteristics (Fig. 7, b ) of which are identical to the corresponding characteristics (Fig. 7, b ) of a single-stage amplifier (Fig. 5, a )

С 2 r ^R 1 - X 3 ( C 2 x + R 1 D c )

X 2 =

( d i r + ^R 1 b_r ) X 3 + c 2 x   ^R 1 d x

^R 3 =

- B 3 ± B 2 3 - ⁴ A 3 C 3

2 A ₃

где

A 3 = ⁽ b r c 2 r ⁺ b x c 2 x ⁺ A 0 ) ^R 1 ⁺ c 2 r d ir ⁺ c 2 x d ix ;

A 0 = ^{( d} 1 r ^{+ R} 1 b r ^{) C} d ^{+ ( d} 1 x ^{+ R} 1 b x ) D c ;

B 3 = ⁽ c 2 x ^d 1 r - ^c 2 r ^d 1 x ⁺ B 0 ) ^R 1 ^{+ R} 2 ⁽ b r c 2 x ^- b x c 2 r ^);

B 0 = ⁽ c 2 x ^{- R} 1 ^d x ^{)( C} r ^{- C} 1 r ^{+ d} 1 r ) -

• - ⁽c2r - ^R1 ^dr⁾⁽cx - c 1 x^{+ d}1 x^);

2. Математическое и схемотехническое моделирование

C 3 = ^R 1⁽ c 2 r ⁺ c 2 x ) - ^R 2 ⁽ c 2 r ^d r ⁺ c 2 x ^d x )•

Оптимизация параметров двухполюсников, свободных от ограничений типа (1)–(44) (то есть находящихся в правой части полученных в данной статье выражений), производится с помощью известных численных методов [10].

На рис. 7–13 для примера показаны принципиальные и эквивалентные схемы однокаскадного и двухкаскадного усилителей с одинаковыми и неодинаковыми каскадами, соответствующие исследуемой структурной схеме с параллельной по напряжению связью, представленной на рис. 1, а , а также их теоретические и экспериментальные характеристики. Использован транзистор типа BFQ17PH (рис. 7, а , 8, 11). Схема НЧ выполнена в виде параллельно соединенных транзистора и ЦОС (П-образного соединения трех элементов

C 78 , R 105 , R 110 ) на однокаскадной схеме (рис. 7, а ) и C ₇₈, R ₁₀ 5 , R ₁₁₀, C ₈₂, R ₁₂₃, R ₁₂₄ на двухкаскадной схеме (рис. 8). Нагрузка и сопротивление источника сигнала выполнены на элементах R ₁₁₄ и R ₁₁₇ соответственно. Схемы СЧ собраны в виде Г-образных четырехполюсников на элементах R ₁₁₉, L 2 (рис. 7), R ₁₁₉, L 2 , R ₁₂₇, L 4 (рис. 8), параметры которых определялись по формулам (3).

Эквивалентная схема нелинейного элемента выполнена в виде перекрытого Т-образного четырехполюсника на элементах R _w, C 9 , R 13 , L ₇, R 11 , L 9 , R 9 , L 5 (рис. 9). Параметры эквивалентной схемы НЭ выбраны из условия совпадения выходного сопротивления НЧ с выходным сопротивлением НЧ с использованием реального транзистора [4]. Схема НЧ реализована в виде параллельно соединенных эквивалентной схемы нелинейного элемента и цепи обратной связи из П-образного соединения трех элементов C ₈, R 19 , R 22 • Параметры ЦОС заданы произвольно. Схема СЧ собрана на основе Г-образного соединения двух элементов R 24 , L 10 • Частотные характеристики принципиальных схем, показанные на рис. 7, б (сопротивления источника сигнала и нагрузки равны 100 Ом) и 8 (сопротивления источника сигнала и нагрузки равны 50 Ом), идентичны. Это соответствует выводам, сделанным на основе анализа полученных ранее [3] выражений для передаточных функций исследуемых многокаскадных структурных схем (рис. 1, а ).

Таким образом, при использовании СЧ также наблюдается новое явление, состоящее в том, что

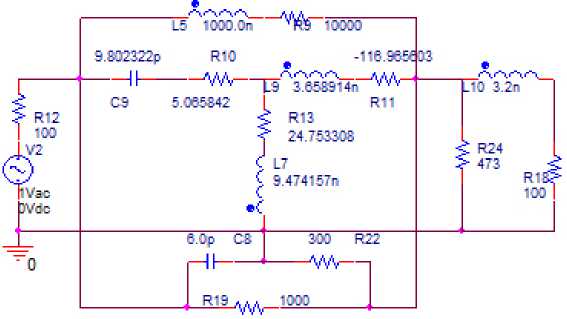
Рис. 9. Эквивалентная схема однокаскадного усилителя (рис. 5, а ), соответствующая структурной схеме (рис. 1, а ), исследуемая в системе OrCad

Fig. 9. Equivalent circuit of a single-stage amplifier (Fig. 5, a ), corresponding to the structural circuit (Fig. 1, a ), studied in the OrCad system

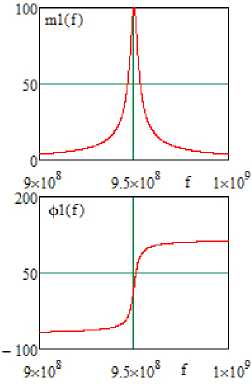
а

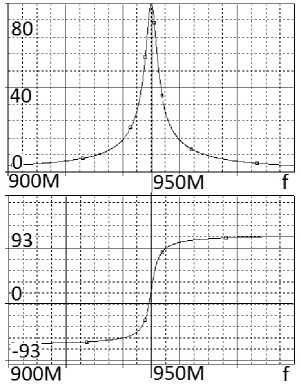
б

Рис. 10. Частотные характеристики (АЧХ и ФЧХ) эквивалентной схемы (рис. 9), полученные в системе MathCad (а) и OrCad (б) Fig. 10. Frequency characteristics (frequency response and phase response) of the equivalent circuit (Fig. 9), obtained in the MathCad (a) and OrCad (b) systems при определенных соотношениях между количеством каскадов и значениями сопротивлений источника сигнала и нагрузки однокаскадного радиоустройства частотные характеристики однокаскадного и многокаскадного радиоустройств оказываются идентичными или подобными [3]. Такие схемы названы эквивалентными.

Анализ также показывает, что экспериментальные (рис. 7, б ) частотные характеристики принципиальной схемы усилителя (рис. 7, а , 8) удовлетворительно совпадают с характеристиками эквивалентной схемы (рис. 9) усилителя, полученными расчетным путем (рис. 10, а ) и экспериментально (рис. 10, б ).

Средняя частота эквивалентной схемы f ® ® 950 МГц (рис. 10, а и б) незначительно отличается от средней частоты принципиальной схемы f « 950,2 МГц (рис. 7, б ).

Значения модулей передаточной функции принципиальной и эквивалентной схем усилителя равны m = 100. Сопротивления РЧ, ЦОС, нагрузки и источника сигнала принципиальных и эквивалентных схем АФМ полностью совпадают.

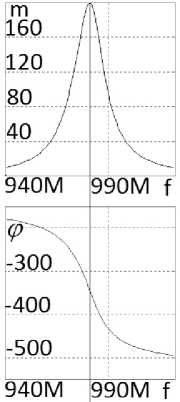
При использовании неодинаковых каскадов возникает возможность значительно увеличить рабочую полосу частот. Например, для двухкаскадной схемы (рис. 11) произведение коэффициента усиления на полосу частот составляет примерно 2100 (рис. 12). Это почти в 7 раз больше, чем произведение коэффициента усиления на полосу частот однокаскадного усилителя или двухкаскадного усилителя с одинаковыми каскадами (рис. 7, б ).

Основные показатели (средняя частота, полоса частот, коэффициент усиления, форма АЧХ, значения параметров) принципиальной (рис. 11, 13, а )

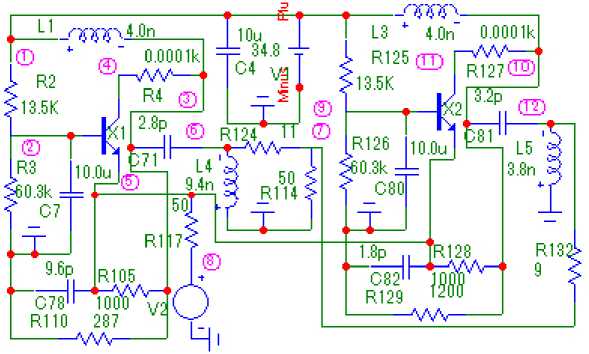
Рис. 11. Принципиальная схема двухкаскадного усилителя с неодинаковыми каскадами, соответствующая структурной схеме (рис. 1, а ), частотные характеристики которого получены в системе MicroCap и изображены на рис. 13, а

Fig. 11. Schematic diagram of a two-stage amplifier with unequal stages, corresponding to the structural diagram (Fig. 1, a ), the frequency characteristics of which were obtained in the MicroCap system and are shown in Fig. 13, a

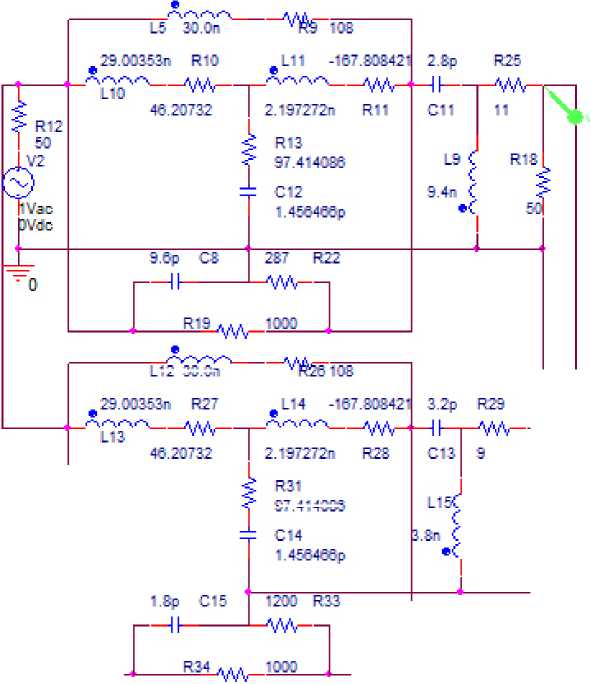
LI 2 30 On

?T 4-4'--

Рис. 12. Эквивалентная схема двухкаскадного усилителя с неодинаковыми каскадами (рис. 11), соответствующая структурной схеме (рис. 1, а ), исследуемая в системе OrCad

Fig. 12. Equivalent circuit of a two-stage amplifier with unequal stages (Fig. 11), corresponding to the structural circuit (Fig. 1, a ), studied in the OrCad system

и эквивалентной (рис. 12, 13, б и в ) схем усилителя с неодинаковыми каскадами совпадают удовлетворительно. Формы ФЧХ этих схем отличаются, что говорит о недостаточном совпадении эквивалентной и принципиальной схем. Характеристики эквивалентных схем, полученные теоретически

(рис. 13, б ) и экспериментально (рис. 13, в ), совпадают полностью.

В работе [12] показано, что результаты схемотехнического моделирования удовлетворительно совпадают с результатами экспериментальных исследований физических макетов радиоустройств.

а

б

в

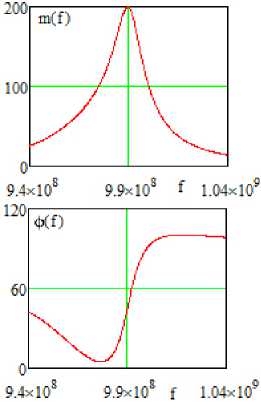
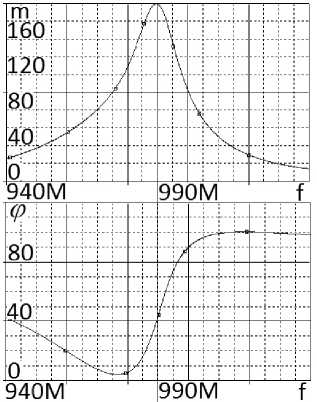
Рис. 13. Частотные характеристики (АЧХ и ФЧХ) принципиальной схемы (рис. 11), полученные в системе MicroCap ( а ), и характеристики (АЧХ и ФЧХ) эквивалентной схемы (рис. 12), полученные в системе MathCad ( б ) и OrCad ( в )

Fig. 13. Frequency characteristics (frequency response and phase response) of the basic circuit (Fig. 11), obtained in the MicroCap system ( a ), and characteristics (frequency response and phase response) of the equivalent circuit (Fig. 12), obtained in the MathCad system ( b ) and OrCad ( c )

Заключение

Таким образом, полученные математические модели СЧ типа (1)–(24) могут быть использованы для технического проектирования усилителей с одинаковыми каскадами типа «НЧ – СЧ». Возможность изменения величины эквивалентного сопротивления источника сигнала и нагрузки путем включения произвольного количества каскадов типа «НЧ – СЧ» значительно упрощает решение многих задач радиоэлектроники [13], например задач обеспечения однонаправленности распространения сигнала и независимости процессов, происходящих в предыдущем и последующем динамических звеньях систем автоматического регулирования. Использование математических моделей (25)–(48) для синтеза неодинаковых каскадов типа «НЧ – СЧ» совместно с известными численными методами [10] приводит к значительному увеличению (в десятки и сотни раз) скорости оптимизации радиоустройств по критерию обеспечения максимально возможной рабочей полосы частот по сравнению с применением для этой цели только численных методов. На практике использовать модели СЧ (1)–(48) надо совместно с результатами работы [9].