Параметрическое сглаживание в минимаксных задачах

Минимаксные (или максиминные) оптимизационные задачи являются важной составляющей инструментария методов принятия решений, таких как: теория игр или исследование операций. При этом их практическое применение ограничивается принципиальной негладкостью функций максимума, от минимума, (или наоборот).

Один из возможных подходов, позволяющих преодолевать затруднения такого рода, может быть основан на. использовании гладких асимптотических оценок зависимостей решения оптимизационных задач от некоторого вспомогательного инструментального параметра.

Продемонстрируем особенности применения данного подхода, вначале на. примере достаточно широко используемого в вычислительной практике метода гладких штрафных функций.

Пусть требуется решить следующую минимаксную задачу: найти минимум и(ж) при условии ж € П, где П С Еп - компакт, а и(ж) = max {fk(ж)} ,                               (1)

/ге [1 ,У ]

причем функции f _k (ж) Ук € [1,7V], непрерывно дифференцируемые на множестве П.

В случае, когда множество П задается системой неравенств вида уфж) 6 0, г = [1,т], задача (1), как показано в [1], равносильна задаче математического программирования: максимизировать по {ж, и} — и, при условиях

/ к (ж) — и 6 0 Ук = [1,V] и                          (2)

уфх) 6 0 Vi = [1, т].

Здесь мы также предполагаем, что функции уфт) Vi Е [1,m], непрерывно дифференцируемые на множестве И.

Функция и(х) в сделанных предположениях непрерывна, но не является дифференцируемой. Поэтому для решения задачи (2) применим метод гладких штрафных функций [2] с вспомогательной функцией

Nm

А(т, х, и)

= -и - ^ Р(т,/k(х) - и) - ^ Р(т,И(х^• k=1г=1

Условия стационарности для функции (3) можно записать в виде системы

' N ЭР/    _  _\       _ m ЭР/   _\_

Е        ^{(х) -и}) • gr^{ad f}k^{(х) +} fsv^p •^{grad ш(х)} = ⁰ ,

. к=1                          Х            ’"1                     "(4)

N ЭР/  ,\

-1 + Д .-     ■(х)-и) =0•

Ее решения и(т) и х(т ), как показано в [3], будут являться непрерывно дифференцируемыми функциями от параметра т, поскольку к условиям (4) применима стандартная теорема о системе неявно заданных функций (см., например, [4]).

Здесь следует также отметить, что решениями системы (4) будут оценки не только минимаксных точек задачи (1) - (2), но и оценки всех других стационарных точек функции (3). Это может потребовать дополнительного исследования при решении именно минимаксной задачи.

Здесь и далее мы будем предполагать, что штрафная функция Р (т, s) дважды непрерывно дифференцируема Vs и Vт >  0, а также удовлетворяет условиям

Р (т, s) > 0

Vs, Vт >  0

іі lim ^Р(т,s) = ( ⁺^, т м+0                0,

s > 0, s < 0,

причем этот предельный переход монотонен. Кроме того, Vт >  0 и Vs должны быть выпол

нены неравенства

⁸А> 0,  ^> 0.

ds         ds2

Заметим, что для конкретной штрафной функции Р (т, s) вид системы (4) может упро

ститься.

Покажем это на примере Р (т, s) = т exp

(:)

. В этом случае

ЭР (s          f k (х) -и          f k (х)           и\

"эі =^exp =^exp          ) =^exp •^exp l^-т)

Поэтому система (4) принимает вид exp ("l) • Д exp (^ • grad/‘(х) + 1eXp (^)

• grad ц(х) = о ,

X

/ й\    і     (fk (х)\ exp     = Е exp         ,

7     k=1        Т где из первого (векторного) равенства можно исключить и, получив

|        f k (х)                    ।     //k (х)       і     /_Уг(х)

exp          • gradfk(х) + exp           • exp         • gradц(х) = о, k=1        т ) х            k=1        т         і=1        т ) х

-        ( N а последнее (скалярное) равенство упрощается до и(т) = т ln ^ exp k=1

.

В качестве примера использования соотношений (6) - (7) рассмотрим две следующие задачи.

Задача 1. Найти минимальные значения функции максимума и(ж)

Г и(ж) > ж2, [ и(ж) > sin4$ на отрезке [— 2, 1].

Решение

Условия (2) в данном случае имеют вид

максимизировать по

{ж, и}

^{- и},

_________________ при условиях: ж2

-

и 6 0 ,

sin4ж -

и 6 0 ,

-

— ж

6 0 ,

-1 + ж 6 0 .

Вспомогательная функция (3) имеет

вид

Л(т,ж,и) = -и-тexp (ж!-^) -тexp (4') ^{т                  т}

-т exp

(

-

-

ж

\

т

-т exp

— 1 + ж

т

.

В то время как уравнение (7) будет выглядеть так

ж2 - и\

- exp I

• 2ж - expf ™® - = • 4cos4x-^т

-

(

( - 1 - ж)

-

т exp

V

V

-

т

+ т exp

⁽~)) • (.....⁽9

( sin 4ж

.       =0.

Наконец, сглаженная аппроксимация функции максимума определяется формулой

и(т)= т In^exp     + exppn4^.

Уравнение (8) на промежутке [-2, 1] имеет три корня, являющихся приближением к точкам жі = 0, ж2 = - = 0.392699082 и жз = 0.669283188, 8

последняя из которых есть корень уравнения ж2 = sin4ж.

Решение получено.

Результаты решения уравнения (8) для разных значений т приведены в табл. 1, а графическое представление задачи 1 показано на рис. 1.

т	ж 1 (т)	ж 2 (т )	ж з (т)
0.50	— 0.166596357	0.413732397	0.723794952
0.25	— 0.124388280	0.398475953	0.704617207
0.10	— 0.077449382	0.392845484	0.688202392
0.05	— 0.046509302	0.392699415	0.679216477
Точное решение	0	0.392699082	0.669283188

Таблица 1

Задача 2 . Найти минимальное значение функции максимума п(ж, у)

| п(ж)  >   ж² + у² ,

( п(ж)  >  10 - (ж + 1)2 - (у — 2))2 , зависящей от двух переменных.

Решение

В данной задаче на независимые переменные явных ограничений нет, поэтому постановка задачи (2) в данном случае имеет более простой вид:

максимизировать по {ж, у, п} — п, при условиях ж2 + у2 — п 6 0 ,

10 — (ж + 1)2 — (у — 2)2 — п 6 0 .

Вспомогательная функция (3) будет иметь вид

А(т,ж,у,п)

= —п — т exp

(

ж² + у²

т

—

—

—т exp

(

10 — (ж + 1)

—

т

(у — 2)

—

Исключение переменной п из системы уравнений (5) выполняется тривиально и дает

—ж exp

(

ж2 + у2

т

—

п

— I + (ж + 1)

exp

—у exp

ж² + у²

—

т

exp

(“)=exp(

ж² + у²

(

—

(ж + 1)2

—

(у — 2)2

—

т

+ (у — 2) exp f

+exp(

exp

10 — (ж + 1)

—

(у — 2)

—

т

—

—

(ж + 1)2

—

(у — 2)2

т

т

п)

= 0,

1 т

= 0,

—

Качественный анализ (см. рис. 2) в этом случае показывает, что система (10) имеет три решения - точки А, В и С.

Точка В - очевидный максимум, имеет координаты ж = —1 и у = 2. Точки А и С являются стационарными точками задачи на условный экстремум вида максимизировать по {ж, у} ж2 + у2, при условии 10 — (ж + 1)2 — (у — 2)2 = ж2 + у2 , имеющей два решения:

А

{ ^3 + 1 -

3+1

} „ С{

—

: 1 —

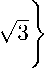
, при этом

точка А является седловой для сглаженной функции максимума, а точка С является

приближением точки минимума функции максимума - решения задачи 2.

Решение получено.

В табл. 2 приведено численное решение задачи (9)—(10) ₉ дающее оценки минимакса для различных значений параметра т.

Таблица 2

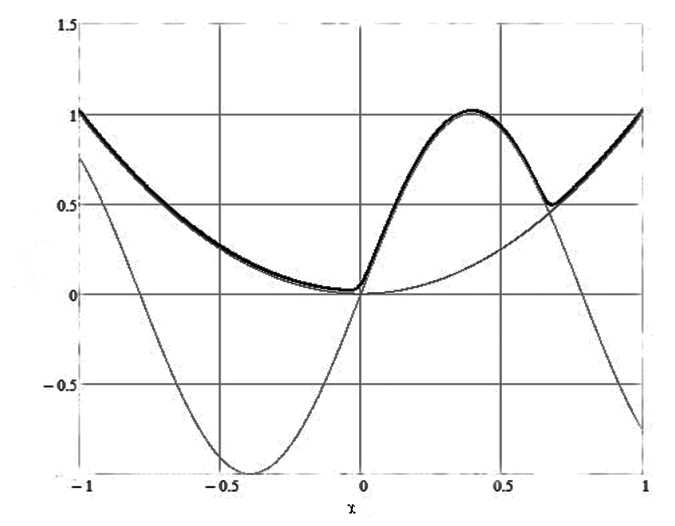
Рис. 1. Графическое представление задачи 1

т	ж ( т )	у ( т )	и( т )
0.50	0.401395490	— 0.802790980	0.931525443
0.25	0.384328458	— 0.768656917	0.799793144
0.10	0.373511177	— 0.747022355	0.721607245
0.05	0.369797284	— 0.739594568	0.695699622
Точное решение	0.366025404	— 0.732050806	0.669872981

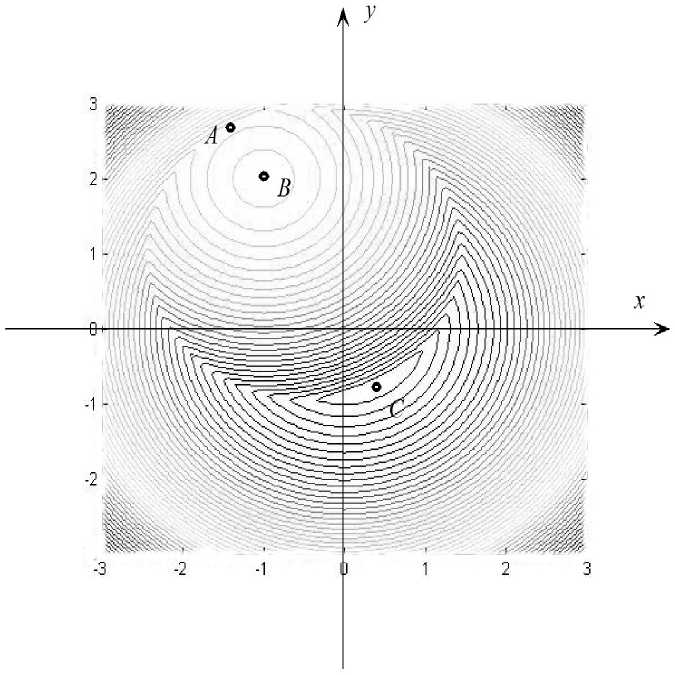
Рис. 2. Система, изолиний функции максимума, в задаче 2

Рассмотрим теперь процедуру построения сглаженной аппроксимации функции максимума. (или минимума), которая может быть выполнена, по схеме, альтернативной методу штрафных функций, а. именно путем использования функций обратных связей, описание и обоснование которого приводится в [5], [6] и [7].

Введем дополнительно к определенной ранее функции Р(t,s) функции Q(t,s) и R(t, s) такие, что Q(t,s) есть обратная по s к строго монотонной по s функции --,, а для ds dR(T, s)

фүіІКШШ R(t, s) Верно   --- = Q ( t, s) .

ds

Вначале кратко опишем основные свойства функции Р ( t,s ) (а также связанных с ней функций), следующие только из их определения.

Пусть функция Р ( t,s), удовлетворяющая условиям (5), имеет непрерывные частные производные по всем своим аргументам до второго порядка включительно для всех т >  0 л Vs.

Тогда для любого фиксированного s < 0

д²Р lim —- = 0 , т ^+0 ds²

ЭР lim —— = 0 II т ^+0 ds а для любого фиксированного s > 0

ЭР lim —— = +х  II т ^+0 ds

д2Р

lim —-у = х . т ^+0 ds²

дР,   .

—— (т, S, можно отнести следу-ds ^х ’

К основным свойствам функции Q(t, s) , как обратной к ющие: она определена и непрерывно дифференцируема при Vt > 0, Vs > 0, а область ее значений есть множество всех вещественных чисел.

Кроме того, она строго выпукла вверх и монотонно возрастает по s при любом фик- 8Р,   .

сированном т >  0, поскольку функция —— Iт, s) определена, положительна, непрерывно 8s '

дифференцируема Vs и монотонно возрастает, и строго выпукла вниз по s.

Также вполне очевидными свойствами функции Q ( t, s ) являются: наличие у нее вертикальной асимптоты вида lim Q ( t, s ) = —то при любом фиксированном т >  0, равно как 5Ю + 0

и выполнение равенства lim Q ( t, s ) = 0 при любом фиксированном s >  0, т >  ■ 0

Важное для дальнейшего свойство функции R ( t, s) описывает

Теорема 1. Для любого фиксированного s >  0 lim R ( t, s ) = 0 . т ю +0

Доказательство

Согласно определению [/-функции R ( t. s), при любом фиксированном а > 0 имеем

S

R ( t , s) = j Q ( t, t) dt .

a

Проинтегрировав правую часть этого равенства по частям, получим

s

^{R ( t}.« ⁾= .q^ ^—«ом -J ^tQ‘^f(T.^t) ^dt.

a

Непосредственно из свойств функции Q(t, s) следует, что при любых фиксированных s >  0 и а >  0

lim sQ ( t s) = 0 и lim uQ (t, а) = 0 .

т ^ +0                      т ^ +0

Для слагаемого с интегралом, в силу правила дифференцирования обратной функции и взаимной обратности функций Q(t, s) и —— (т, s) , будет верно при —— (т, w(s)^ = s os                           os \       7

s

s

I = У tQ f (T,t)dt = j

tdt

s

7 = /

a

a

a

f

tdt д 2Р/      \ dtnT,w(t))

Затем, применив интегральную теорему о среднем [8], получим, что найдется такое фиксированное положительное q Е [а, s], для которого

s

I =

q Г              q . х dt =--------------(s — а) .

• ⁸ 2^Р,    х .           ⁸"^Р,    X

• 8.2 ^(T.^q) “           8Л ^(T.^q)

Последнее выражение стремится к нулю при т ^ +0 в силу соотношения (11).

Теорема доказана.

Суть рассматриваемого подхода заключается в том, что для исходной задачи математического программирования вида максимизировать по ||ж|| = || ^1, ^2,..., ^n^T достаточно гладкую функцию F(ж) при условиях: ^j > 0 Vj = [1,п], /»(ж) 6 0 Vi = [1,rn], где функции /і(ж) Vi = [1,ш] также достаточно гладкие, строится вспомогательная функция т         тп

и(т,ж, Л) = Ғ(ж) - ^ Xifi(x) + ^ R(T,Xi) - ^ r(t,£j), i=1            i=1

ИЛИ тп

и(т, Ж Л) = Цж,Л) + ^ R(T, хг) - ^ r(t, Cj) , i=i

т где L(ж, Л) = Ғ(ж) — 52 Хifi(ж) - стандартная функция Лагранжа.

г =1

Условия стационарности этой вспомогательной функции имеют вид

dL _ . дХ^ Л) dL . д^(ж,Л) = — Q(т, Хг)     Уг = [1,ш] , _                                         (12) =     Q(т,Cj)     VJ = [1,^], причем для регулярных задач, как показано в [5], [6] и [7], lim ж(т) = ж*, п lim Л(т) = Л* , т м+0               т м+0

где ж* и Л* - точные решения исходной задачи математического программирования.

Конкретно, в случае минимаксной задачи (2) функция Лагранжа будет

N             т

L(ж, п, И, Л) = —п — ^ ш_к f k k (ж) — п) — ^ Х г у г (ж), к =1                    i =1

а условия стационарности (12) соответственно имеют вид:

—(ж,п, fi,Л) °s j	= д(тл3 )	Vj = [1,п] ,
dL,- - ж —(ж,п, И, Л) дп dLM-+.^	= 9(т,п),	(13)
дх(ж,п,И,Л)	= — 9(т,Хг)	Уг = [1, ш] ,
dL    __ -—(ж,п,И,Л)	= — 9(т,Шк )	Vk = [1,^] .

Совместно вектор-функция ж(т) и скалярная функция п(т) образуют непрерывно дифференцируемую по т аппроксимацию решения минимаксной задачи (2). Непосредственное использование системы условий (13) продемонстрируем на примере следующих задач, для решения которых возьмем (как предложено в [7]) Р (т, s) такую, что

Q(т,s)

=т (s—9-

Задача 3.

Найти минимальное значение функции п(ж, у) = max{ 2 — 2ж; ж } при усло виях ж > 0;

ж 6 р для р =2

II р = 1.

Решение

Запишем условие задачи в виде максимизировать 0 • ж + (—1) • и при условиях ж > 0 , и > 0,

—2ж — и 6 —2 , ж — и 6   0 , ж 6   р.

Нетрудно убедиться, что решением этой минимаксной

и* = ж* = 1, а при р = 1 - и* = ж* = 3.

задачи при р

2 будет

Система уравнений (13) в этом случае имеет вид:

• —2 — 2A1 + A2 + A3

1 — Ai — A2

• <          2 — 2ж — и

• ж — и
• —р + ж

  _-

  _-

• т

т

т

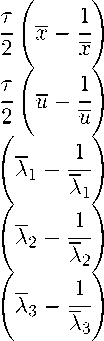
Результаты расчетов приведены в табл. 3.

Таблица 3

т	и для р = 2	и для р = 1
0.1	0.912994245	0.741263714
0.01	0.985411722	0.673919921
0.001	0.998503843	0.667389209
0.0001	0.999850038	0.666738892
0.00001	0.999985000	0.666673889
0.000001	0.999998500	0.666667389
0.0000001	0.999999850	0.666666739
0.00000001	0.999999985	0.666666674
Точное решение	1	2 3

Решение получено.

Применим метод функций обратных связей в нелинейной задаче, имеющей решение, совпадающее с одним из решений задачи 1.

Задача 4. Найти на промежутке [2; 1] минимум функции максимума и(ж)

( и(ж) > ж2, [ и(ж) > sin4ж.

Решение

Запишем условия задачи в виде максимизировать по {ж, и} — и, при условиях ж² — и 6 0 , sin 4ж — и 6 0 ,

В данной задаче функция Лагранжа будет

Е(ж, и, Ai, А₂) = —и — А1(ж² — и) — A₂(sin4ж — и).

Соответствующая ей система уравнений (13)

—

—

т

т

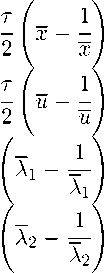
—2 А1ж — 4 A2 cos 4ж

—1 + Ai + А2

и — ж²

и — sin 4ж

Эта система на промежутке [2, 1] имеет решение ж(т) - приближение к ж = 0.669283188, являющемуся корнем уравнения ж2 = sin4ж.

Решения системы уравнений (14) для разных значений т приведены в табл. 4.

Таблица 4

т	ж ( т )	и ( т )	А 1 ( т )	А 2 ( т )
0.1	0.644421822	0.391810461	0.792480392	0.315541808
0.01	0.666512412	0.441084537	0.733141487	0.275988786
0.001	0.669003439	0.447243056	0.728185244	0.272709094
0.0001	0.669255187	0.447870180	0.727700682	0.272388564
0.00001	0.669280387	0.447933004	0.727652337	0.272356586
0.000001	0.669282908	0.447939287	0.727647504	0.272353388
0.0000001	0.669283160	0.447939916	0.727647021	0.272353069
0.00000001	0.669283185	0.447939978	0.727646972	0.272353037
Точное решение	0.669283188	0.447939985	0.727646967	0.272353033

Решение получено.

В заключение рассмотрим случай задачи поиска максимина следующего вида:

на произведении компактов X С Е ^п и У С Е^т для непрерывной функции Ғ (х, у) найти Ғ * = max min Ғ(x,y^ .

х е х y e ¥

Эта задача, как показано в [1] и в [9], может быть сформулирована в виде задачи математического программирования с неограниченным числом ограничений:

найти Ғ * = max и при условиях

{х,и} j x EX, [ Ғ (x, y) > и Vy ЕУ.

В монографии [9] (гл. 1, § 5) показано, что метод штрафных функций допускает свое использование для решения задач подобных классов, причем в качестве штрафующей суммы

Ғ(x,y)) dy.

в (2), применяя интегрирование по Лебегу, можно взять S (т, х) = f РІт,и ¥

-

Вспомогателвная функция при этом будет

А(т, x,u)=u -IР (т,и — Ғ (x, y)) dy. ¥

Кроме того, если Ғ (x,y) выпукла вверх по x, то и А(т, x,u) будет выпукла вверх по х, а если Ғ(x,y) непрерывно дифференцируема по x, то и А(т, x,u) будет непрерывно дифференцируемой, и в этом случае условие стационарности функции (16) еств система равенств

дА

= 1 ди дА

-

,др

¥ ^т,^и -^Ғ (^x,^y

дҒ (x,y)

. ^Әж з

-

г др

¥ -^Ғ (^x,^y

' ди дҒ (x,y) д^

dy = 0,

dy = 0     Vj = [1,n] .

Вывод формул (15) и (16) приведен в [9] для штрафных функций внешнего типа, однако эта схема оказывается применимой и для гладких штрафных функций, удовлетворяющих условиям (5). Строгое доказателвство этого факта выходит за рамки данной статьи, однако его можно проиллюстрировать следующим примером.

Рассмотрим задачу отыскания глобального экстремума непрерывной на некотором отрезке [а, Ь] функции Ф(х). При поиске максимума эта задача сводится к задаче математического программирования:

минимизировать Ғ(х,и) = и при условиях Ф(х) 6 u Vx = [а, Ь] .

s

Если взять Р(т, s) = т exp     , то подлежащая максимизации вспомогательная функ- т пня будет А(т, и) = —и

-

b т J exp

a

——---I dx , а ее условие стационарности по перемен-^т

ной u

—1 +

b /              \

Ф(x) — Ц

J expl a         x             z

dx = 0.

Откуда exp

и ^b      Ф(x)

= exp          dx,

\т) a \ Т )

_           b      Ф(х)

что лает и(т) =т ln J exp         dx. Нетрудно а \ т /

убедиться, что оценка для глобального минимума представляется формулой аналогичного

1 ^Ь 7 Ф(x)^ у вида: и(т ) = —т ln exp — dx .

а \ т /

В заключение применение этих формул продемонстрируем на примере следующей простой задачи.

Задача 5. Найти максимальное и минимальное значения функции Ф(ж) = 2 — |ж| на отрезке [—1, 3].

Решение

Для использования формулы (17) предварительно необходимо вычислить ch

)■

j exp--- •—- dx = 2т f exp--

-1

Понятно, что величина выражения т 1п2т | expch —| не очень наглядно представ-т т ляет максимальное значение исследуемой функции на отрезке [—1, 3]. Поэтому найдем также и и* = lim и(т) = lim т ln 2т exp ch =2 . т м+0       т м+0             т т

Аналогично для оценки величины и* предварительно находим

• ³     ( 2 - |ж|\           /

  - 2 exp (-т)у

  
  

  1 ch

  
  

exp I--I dx = 2т I I

1 ch

- 2exp (-т))]=-1 ■

и окончательно:   и* = lim и(т) = — lim т ln 2т К т м+0         т м+0

Нетрудно проверить, что глобальный максимум достигается в точке ж = 0, а глобальный минимум в точке ж = 3.

Решение получено.