Параметризация алгоритмов идентификации электрического диполя

Своевременное обнаружение грозовых очагов и прогнозирование их развития является актуальной задачей. В работе [1] приведено множество примеров применения информации о грозовых очагах в решении различных проблем, связанных с безопасностью жизнедеятельности.

Одним из подходов к моделированию молниевых разрядов является представление его в виде точечного источника электромагнитного излучения (т.е. электрического диполя) находящегося над плоскостью с бесконечной проводимостью. Модель электрического диполя достаточно хорошо описывает большое количество разнобразных внутриоблачных разрядов. Поэтому задача идентификации местоположения электрического диполя по его электромагнитному полю индуцируемому в точке наблюдения над плоскостью с бесконечной проводимостью, представляет большой интерес. Данной проблеме посвящено множество работ, опубликованных в ведущих отечественных [2 – 5] и международных изданиях [9 – 13].

Рассматриваемая задача, как и большинство обратных задач математической физики, является плохо обусловленной. Следствием этого является высокая чувствительность алгоритма к погрешностям в исходных данных и погрешностям вычисления. Аналитическое и численное исследование ряда алгоритмов [2, 13, 14] показывает необходимость предобработки наблюдаемых сигналов, причем параметры оптимальных фильтров определяются спектральными характеристиками источника электромагнитного излучения (ЭМИ) и расстоянием до него. Таким образом, для оценки местоположения источника ЭМИ необходимо иметь оценки его характеристик, получить которые можно зная оценки местоположения. В работе предлагается разорвать указанный выше порочный круг применением параметризованного семейства алгоритмов с последующей статистической обработкой полученных результатов.

Среди возможных методов определения параметров положения произвольно ориентированного электрического диполя, в работе будет рассмотрена параметризация прямого метода [8, 2] и экстремального параметрического метода [3, 10]. Однако заметим, что для повышения статистической значимости оценки параметров следует использовать по возможности большее число алгоритмов.

1.    Математическая модель

Задачу определения дальности до произвольно ориентированного дипольного источника излучения в радиусе до 100 kM можно решить, используя диапазон СДВ. Вполне адекватной математической моделью земной поверхности для рассматриваемых расстояний и длин волн является бесконечно проводящая плоскость. Как показано в [8], ортогональные проекции компонент поля, индуцируемого в точке наблюдения электрическим диполем, размещенным над бесконечно проводящей плоскостью, равны ez (t) = q(t) • v + q‘(t) v + q’’(t) -U, a a2

hxoy(t)= qq')t) 1+ q‘‘(t)aL) , ex(t) = ey (t) = hz (t) = 0.

Здесь a = c/r - величина, обратная времени распространения волны от источника до точки наблюдения, переменные u, v – неизвестные параметры положения источника излучения, q ( t ) — неизвестный дипольный момент источника излучения, r - расстояние до источника излучения.

Компоненты e _z , h _xoy могут быть измерены с помощью антенной системы, состоящей из вертикальной электрической антенны и пары взаимно ортогональных рамочных магнитных антенн и, следовательно, использованы в качестве исходных данных для решения задачи оценки размещения диполя.

2.    Прямой алгоритм и его параметризация

В работах [8, 2] предложен и исследован алгоритм определения параметров u, v и α, заключающийся в прямом вычислении где

/ hf 2 a =

V h 2 f o

^{— h} 2 ^f i

, - h i f i

u =

^f 0 ^f 2 ^{- f} 1

^h 2 ^f 0

,

- h i f i

go + foa v = —~----, h0a

∞ f k = j eZk^(t)hXkOy (tw,

∞ hk = j (hkoy(t)) dt, 0

∞ g k = j eZk+i) (t)hXkOy (t^dt,

k = 0,1, 2. (5)

Для повышения степени разнообразия сигналов от источника с заданными параметрами положения можно использовать предобработку измеренных сигналов e z (t) , h _xoy (t) линейными фильтрами [16].

Спектр молниевого разряда лежит в достаточно узком диапазоне частот, поэтому применение полосового фильтра с подходящими нижней Q и верхней Q частотами среза позволит максимально использовать всю полезную информацию, которую несет сигнал, и ослабить влияние присутствующих в сигнале шумов. Поскольку параметры положения и спектр источника излучения не известны, то будем строить множество оценок

E1 = {(ai, Ui, vi) : i = 1, 2,..., N} для семейства полосовых фильтров

F iM^^{1 ,} если ^{Ш E} [^i , ^ i] ^, i = 1, 2,...,N. I 0, в противном случае,

Элементы множества E будем рассматривать как реализацию векторной случайной величины, а для оценки истиных параметров положения u , v и α применять методы статистического робастного оценивания.

3.    Экстремальный алгоритм и его параметризация

Прямой алгоритм был получен в предположении, что источник излучения является диполем, а подстилающая поверхность – плоскостью с бесконечной проводимостью. В силу неидеальности моделей и наличия шумов в наблюдаемых сигналах, приходится допускать наличие невязок в полученных уравнениях. Поэтому, с интуитивной точки зрения предпочтительней использовать принцип наименьших квадратов, в соответствии с которым параметры модели определяются из условия где

∞

I ^{( x )}= J

A =

t

^x 1 e z + ^x 2 e z + ^x 3 ^h xoy + ^x 4 h xoy + ^x 5

j h xoy ( т ) dT dt = ( x , Ax )

^ min, x

∞

s · s ^T dt,

s=(

k • e ‘ (t)

e (t)

k • h ‘ (t)    h (t)

k у ■ ^{( T} > ^dT) -

k – постоянная времени дифференцирующего и интегрирующего звеньев, введенная для согласования масштабов координат вектора x.

Пусть собственные числа матрицы A упорядочены: A q <  Л 1 <  Л ₂ <  А з <  Л ₄ , и пусть x ⁽⁰⁾ , x ⁽¹⁾ , x ⁽²⁾ , x ⁽³⁾ , x ⁽⁴⁾ – соответствующие им собственные векторы.

Экстремальный алгоритм [3, 10] определения параметров u, v и α, устойчивый к ошиб- кам в исходных данных состоит в выполнении следующих шагов.

Пусть A _mn — определитель матрицы, полученной из матрицы (x ⁽²⁾ , x ⁽³⁾ , x ⁽⁴⁾) путем удаления строк с номерами m и n .

Вычислить ka12 = <

2A 25

• ^{—    A} 24 ^{- A} 15 ± у ^(A 24 + ^A 15 ^{) 2 - 4A} 14 ^A 25

• —    A 24 — A 15 ^ J (A 24 + A 15 ) ² — 4A 14 A 25

если | A 25 I >  | A i₄ | ,

2A 14

в противном случае,

= ko n A i^ +A ^a ^A 12

v n

^{— A} 45 ^ka n ^A 24 ^{+ A} 25 ,

П = 1, 2.

Пусть

n * = arg    min      ( 1,ka n — u n — ka*, — k ² a n 2v_n \ A ( 1,ka n — U n , — ka n v n — k ² a n ² vJ T .

n G{ 1, 2: a n >0 } L^{x                                            7                                                 7} J

Положить

a( A ) = a n * , u( A ) = u n * , v( A ) = v n * .                         (11)

Параметризацию экстремального алгоритма осуществим также как и параметризацию прямого алгоритма, т.е. построим множество оценок

E2 = {(a(Ai), u(Ai), v(Ai)) : i = 1, 2,..., N} для семейства полосовых фильтров Fi, i = 1, 2,..., N используемых для предобработки измеренных сигналов. Элементы множества E2 также будем рассматривать как реализацию случайной величины, а для оценки истиных параметров положения u, v и α применять методы статистического робастного оценивания.

4.    Эффективная реализация алгоритмов с применением преобразования Фурье

При выполнении приведенных выше алгоритмов необходимо вычисление величин

ОО

4=7

^ hk = [ №

dt, k E { 0,1 } ;

dt, k E {- 1, 0,1 } ;

где e i (t) , h i (t) — результаты предобработки

ОО fk = /e^toh^W k E {0,1};

ОО gk = j «У^У^ (t)dt, k E { —1,0};

сигналов e z (t) и h xoy (t) с помощью фильтра

F i , i = 1, 2,...,N . С целью повышения эффективности алгоритма, значения переменных f k , h k , g k целесообразно вычислять, применяя преобразование Фурье

( E M, HM) = F (e z (t) ^, h xoy (t)) .

Действительно, представление переменных f k , h k , g k в терминах преобразования Фурье с учетом равенства Парсеваля имеет вид

Ωi kk = I M2k| E(^, 2d_.

Ω ^ˆ i

ˇ hk = [Qi . ■ |h(^)|2d^,

Ω i

ˇ fk = ^ i ..  Re (e(oW) d^,

ˇ gk = / M2kIm (^B(^)HИ) d^, Ωi k E { —1,0,1,2},

i = 1, 2,...,N.

Поэтому для вычисления всех интегралов f k , h k , g k , k E {— 1,0,1, 2 } , i = 1, 2,..., N потребуется не более O(T log ₂ T + NT) операций, здесь T - количество отсчетов в наблюдаемых реализациях e _z , h _xoy .

Используя алгоритм (4) и значения f k , h k , g k , k E { — 1, 0, 1, 2 } , i = 1, 2, ..., N, построим следующее множество оценок положения источника излучения

- jV      /hlf

¹ = IVi = УЖО"

-

h ⁱ2 f 1ⁱ

— h l f l

^U i ⁼

ii

f0f2

-

(f l ) ²

h 2 f 0 — h l f l

v i = ^g 0 + / 0 ^a i : i = 1, 2 ,...,nL   (12)

h ⁱ ₀ α i

Используя алгоритм (8)-(11) и значения f k , h ^ , g k , k E { — 1, 0, 1, 2 } , i = 1, 2, ..., N , построим следующее множество оценок положения источника излучения

E 2 = { (a( A i ), u( A i ), v( A i )) : i = 1, 2,...,N } ,                        (13)

где

	i e 1 0	0 e o	f 1i -go	i g 0 f 0i	- f 0o g - 1
A i =	f 1i	- g o	h i 1	0	-h 0
	i g 0	f 0i	0	h ' h 0	0
	- f oi	g - 1	-h 0	0	h i - 1

5.    Вычислительный эксперимент

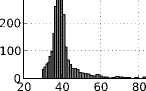
Для проведения вычислительного эксперимента с помощью имитационного моделирования [15] были сгенерированы сигналы e z (t) , h xoy (t) от двух источников, расположенных на расстоянии 40 и 120 километров. В качестве функции источника использовалась аппроксимация, предлагаемая в работе [17]. Для оценки возможности использования алгоритмов в реальных условиях в сигналы необходимо добавить шум. Для моделирования шума в сигналах используется известный факт, что ошибку квантования сигнала по уровню можно рассматривать как белый шум: ошибка квантования является случайным процессом, при этом с уменьшением числа используемых для представления сигнала уровней растет мощность шума квантования. Число используемых уровней квантования, в нашем случае это 2 7 = 128 и 2 8 = 256 уровней, определяет точность представления данных, а следовательно и уровень шума.

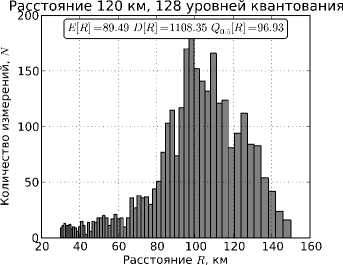
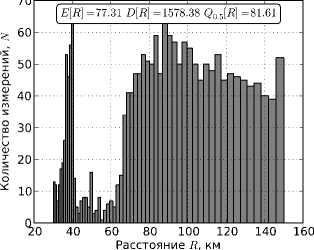
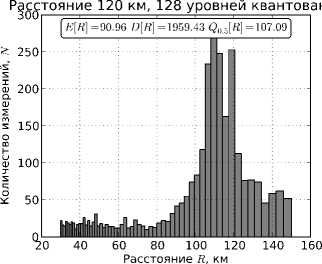
На рис. 1 представлены гистограммы оценок дальности по множеству E 1 (12), полученные прямым алгоритмом (4) в результате обработки смоделированных сигналов. На рис. 2 представлены гистограммы оценок дальности по множеству E 2 (13), полученные экстремальным алгоритмом (8)–(11) в результате обработки смоделированных сигналов.

Из приведенных гистограмм можно сделать следующие выводы: (1) наличие шумов существенно влияют на работу рассматриваемых алгоритмов, (2) повышение уровня шума заметно увеличивает дисперсию значений результатов отдельных измерений алгоритмов, (3) экстремальный алгоритм работает существенно лучше прямого алгоритма для дальних источников излучения, (4) статистики: среднее значение E [R] , выборочная медиана Q o.5 [R] и выборочная дисперсия D[R] , - дают относительно приемлемые оценки дальности.

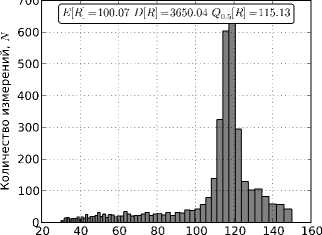
Повысить качество оценивания можно объединив множества оценок E 1 и E 2 . На рис. 3 представлены гистограммы оценок дальности по множеству E = E i U E 2 всех оценок. Из рис. 3 видно, что для сгенерированных сигналов построенные по множеству E статистики: среднее значение E [R] , выборочная медиана Q o.5 [R] и выборочная дисперсия D[R] , – дают более достоверные результаты, чем статистики по множествам E 1 и E 2 .

Большое разнообразие результатов измерения не позволяет строить достаточно точные гарантированные оценки параметров u , v и α . Все данные, полученые в результате работы параметризованных прямого и экстремального методов требуют дополнительной фильтрации. Для построения фильтрующих функционалов будем использовать метод антитрасс [18] и метод проектирования [9, 10, 13].

Метод антитрасс [18] основан на восстановлении функции источника q(t) по сигналам e z , h xoy . При безошибочных значениях оцениваемых параметров u , v и а решение q Uv^a (t) дифференциального уравнения (1) должно совпадать с решением q Uv^a (t) уравнения (2). Это

Р^стояние 40 км, 128 уровней квантования £[/?] -37.61 Р[Д] -127.28 QqJA] ~38Лр]

700 -

600 -

Р^стояние 40 км, 256 уровней квантования

5[Я] -39.64 Р[Я] -89.14 Qp.^T?] -40.29]

1400-

= 1200-

^ 1000-

800 -

600 -

400 -

200 -••

Расстояние 7?, км

100  120  140  160

%   40   60   80   100 120 140 160

Расстояние R, км

Рс^стояние 120 км, 256 уровней квантования

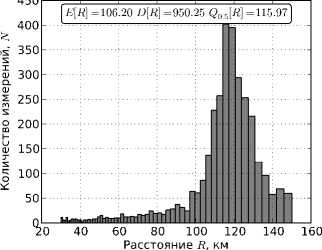
Рис. 1. Гистрограммы оценок дальности прямым алгоритмом

Расстояние 40 км, 128 уровней квантования

Расстояние R, км

Расстояние 40 км, 256 уровней квантования

Расстояние 120 км, 256 уровней квантования

Расстояние R, км

Рис. 2. Гистрограммы оценок дальности экстремальным алгоритмом

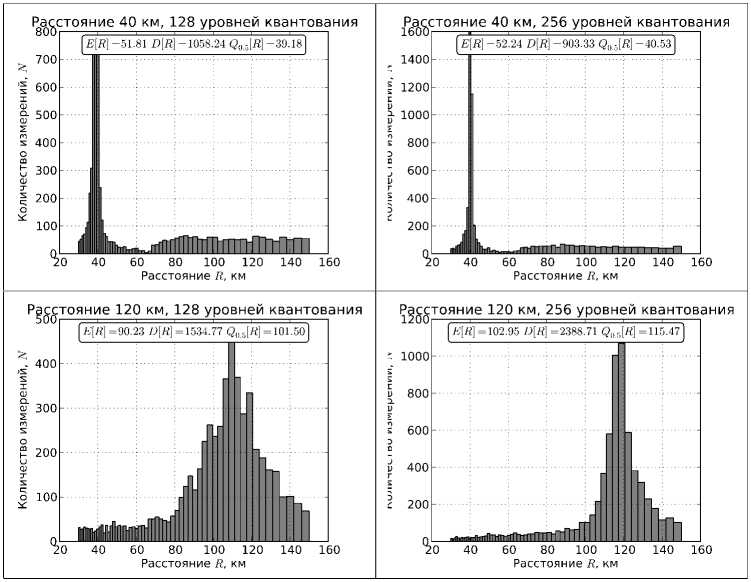
Рис. 3 . Гистрограммы распределения множества всех оценок дальности

позволяет для фильтрации вариантов предложить функцию потерь

L ( u,v,a ) = \^ ^а ( 1 ) — qT^ W =

E(w)              H (w)

— uw" ² + jwva + va ²    — w ² + jwa

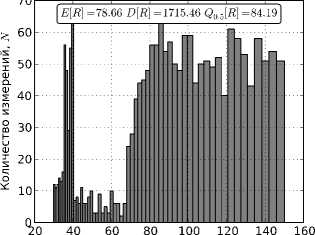
Заметим, что при (u, v,a) = 0 алгоритм вычисления значения L ( u, v,a ) является вполне устойчивым, а сама функция L ( u, v,a ) непрерывна. На рис. 4 представлены гистограммы оценок дальности по множеству оценок E l = { (u, v, a) G E : L ( u, v, a) <  L o } .

Метод проектирования [9, 10, 13] основан на проектировании прообраза вектор-функции (e z , h xoy ) на линейное многообразие L решений системы дифференциальных уравнений (1)(2). При безошибочных значениях оцениваемых параметров u , v и α существует решение q, удовлетворяющее системе дифференциальных уравнений (1)–(2), т.е. прообраз пары сигналов (e z , h xoy ) принадлежит L , и длина проекции максимальна. Это позволяет для фильтрации вариантов использовать длину проекции в качестве функции пополезности. В терминах преобразования Фурье функция полезности имеет вид [9, 10, 13]

U ( u, v, a) =

E(w)( — uw ² — jwva + va ² ) + H (w)( — w ² — jwa) | — uw ² + jwva + va ² | ² + |— w ² + jwa \ 2

При ( u, v,a ) = 0 алгоритм вычисления значения U ( u,v,a) является вполне устойчивым, а сама функция U ( u,v, a) непрерывна. На рис. 5 представлены гистограммы оценок дальности по множеству оценок E u = { (u, v,a ) G E : U ( u,v,a ) >  U o } . Из рис. 4 и рис. 5 видна эффективность использования фильтрации для рассматриваемых сигналов.

Введем теперь мнжество оценок

E = { (u, v,a ) G E : U ( u,v,a ) >  U o , L(u,v,a) <  L o } .

Р^стояние 40 км, 128 уровней квантования

[ АДК] =38-31 ОД =63-85 Q().r,[«] =зоТбз]

Р^стояние 40 км, 256 уровней квантования

[ АДК] =39.33 ОД =42.72 ФОД =40Л7]

350 -

300 -

250 -

200 -

150-

100-

io 40   60   80   100 120 140 160

Расстояние R, км

50 - qI кишишь ,--^—^—^—^—^

20   40   60   80   100 120 140 160

Расстояние R, км

Расстояние 120 км, 128 уровней квантования зоо

[ОД] = 110.09 ОД] = 1267.02 ОД[К] =120.85 ]

Расстояние 120 км, 256 уровней квантования

(ОД =116.24 ОД] =31.92 фОД] =116.80 ]

%  40

60   80   100 120 140 160

Расстояние R, км

400 -

300 -■

200 -

100-

%  40

60   80   100  120  140 160

Расстояние R, км

Рис. 4. Результаты фильтрации по функции потерь

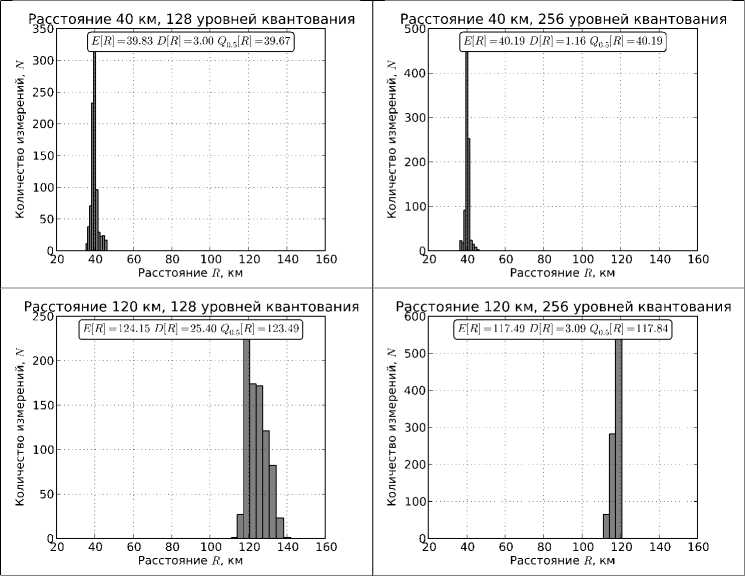
Рис. 5 . Результаты фильтрации по функции полезности

Р^стояние 40 км, 128 уровней квантования [ОД] -39.83 ОД] -3.27 ОДД] -З9.бб]

Р^стояние 40 км, 256 уровней квантования

[ОД —40.15 ОД -1.26 QoJ-R] -40.17]

... 350 -■

’| 300 - ф 200

250 -■

200 -

150--

100-

50--

%   40   60   80   100 120 140 160

Расстояние 7?., км

О1----^—^-ОД—ОД—ОД—ri.

20   40   60   80   100  120  140  160

Расстояние R, км

Р^^тояние 120 км, 128 уровней квантования

(ОД] =122.62 ОД =14.92 Q„ JK] = 122.061

Р^^тояние 120 км, 256 уровней квантования

150-

[ь]К] =116.57 ОД] =2.40 ОД[К] = 117.02]

250 -

ф 200 -

150-

100--

50-

%   40   60   80   100 120 140 160

Расстояние R, км

0^--^--^--^--,'    —ОД—г*

20   40   60   80   100 120 140 160

Расстояние R, км

Рис. 6. Гистрограмма оценок дальности по множеству E

В множество E включены оценки, удовлетворяющие условиям фильтрации как по потерям, так и по полезности. На рис. 6 представлены гистограммы оценок дальности по множеству оценок E . Рис. 6 показывает эффективность применения совместной фильтрации по функции потерь L и по функции полезности U .

6.    Заключение

Предложенный в статье метод решения обратных задач для систем линейных дифференциальных уравнений с постоянными коэффициентами, заключающийся в применении к результатам наблюдения параметризованного множества алгоритмов с последующей фильтрацией и статистической обработкой результатов, является вполне конструктивным и работоспособным.

Работа проводилась при финансовой поддержке РФФИ, проект № 10-07-96003-р_урал_а