Параметризация задачи Коши для нелинейных дифференциальных уравнений с контрастными структурами
Автор: Кузнецов Евгений Борисович, Леонов Сергей Сергеевич, Цапко Екатерина Дмитриевна
Журнал: Инженерные технологии и системы @vestnik-mrsu
Рубрика: Физико-математические науки
Статья в выпуске: 4, 2018 года.
Бесплатный доступ
Введение. В статье приводятся результаты анализа численных методов решения задачи Коши для нелинейных обыкновенных дифференциальных уравнений с контрастными структурами (внутренними слоями). Подобные уравнения моделируют различные прикладные задачи гидроаэромеханики, химической кинетики, теории каталитических реакций и т. д. Получить аналитическое решение этих задач удается редко, а их численное решение сопряжено со значительными трудностями, связанными с плохой обусловленностью в окрестности пограничных и внутренних слоев. Целью статьи является анализ области применения традиционных численных методов к решению задач данного класса и апробация альтернативных методов решения. Материалы и методы. Для численного решения задачи Коши используются традиционные явные методы Эйлера и Рунге-Кутты четвертого порядка точности, а также неявный метод Эйлера с постоянным и переменным шагом. В качестве альтернативы предложено использовать метод продолжения решения по наилучшему аргументу, который заключается в замене исходного аргумента задачи на новый, отсчитываемый вдоль интегральной кривой задачи. Переход к наилучшему аргументу позволяет получить наилучшим образом обусловленную задачу Коши. Результаты исследования. На примере решения тестовой задачи показаны вычислительные затруднения, возникающие при решении уравнений с контрастными структурами традиционными явными и неявными методами. Они выражаются в значительном уменьшении шага интегрирования в окрестности пограничных слоев, что приводит к увеличению времени счета и усложнению процесса решения сверхжестких задач. Достоверность полученных результатов подтверждается сопоставлением с аналитическим решением и известными работами других авторов. Обсуждение и заключение. Результаты вычислительного эксперимента демонстрируют применимость традиционных методов решения задачи Коши к уравнениям с контрастными структурами лишь при малой жесткости, в остальных случаях данные методы малоэффективны. Показано, что метод продолжения решения по наилучшему аргументу позволяет снять большинство недостатков, присущих непреобразованной задаче. Это отражается в снижении времени счета и увеличении точности полученного решения.
Контрастные структуры, метод продолжения решения, наилучший аргумент, плохая обусловленность, задача коши, обыкновенное дифференциальное уравнение
Короткий адрес: https://sciup.org/147220594
IDR: 147220594 | УДК: 517.91 | DOI: 10.15507/0236-2910.028.201804.486-510
Текст научной статьи Параметризация задачи Коши для нелинейных дифференциальных уравнений с контрастными структурами
ных задач Коши, но не могут сравниться по быстродействию с явными методами, т. к. на каждом шаге неявного метода приходится решать систему нелинейных уравнений. Этот недостаток удается устранить при помощи метода продолжения решения33, который заключается в замене исходного аргумента задачи Коши на новый. Можно выбирать различные аргументы продолжения решения, но наиболее часто используют наилучший аргумент. Данный аргумент отсчитывается по касательной к интегральной кривой рассматриваемой задачи и обладает рядом исключительных свойств. Для задачи (3)-(4) наилучший аргумент X записывается в скалярной форме:
dX1 = dy 1 +-----+ dy 2 + dt 2. (9)
Будем полагать, что все переменные у1,у2,...,yn и аргумент t зависят от X. Дополняя систему (3) соотношением (9) и разрешая полученную систему относительно производных по λ, получим преобразованную систему dyi _ fi (t,У1,^,Уп)
d^ Q(t,Ух,-,Уп) ’ dt _ 1
d^ Q (t, У1,^, Уп) ’ i _ 1,..., n,
где
_____________ Q ( t , У 1 , ^ , y „ )= ________________ = 71 + ft ( t , yv-, У п ) + - + f 2 ( t , yv-, У п ) .
Начальные условия (4) для системы (10) перепишутся в виде
Задача (10)-(11) обладает рядом важных для численного решения свойств34:
-
1. Квадратичная норма правой части системы (10) равна единице, т. е. устраняются все вычислительные трудности, связанные с неограниченным возрастанием правых частей системы (3).
-
2. Обусловленность системы (10) является наилучшей.
-
3. Показатель жесткости преобразованной системы (10) меньше, чем у исходной.
Все отмеченные свойства дают возможность решать преобразованную задачу (10)-(11) любыми численными методами, в том числе и явными.
Далее рассмотрим применение указанных методов к решению задачи Коши для систем дифференциальных уравнений с контрастными структурами.
Результаты исследования
В статье А. А. Белова и Н. Н. Калит-кина [3] для проверки эффективности численных методов при решении задач с контрастными структурами предложен ряд тестовых задач. Проанализируем решение одной из этих задач, называемой степенным тестом.
Постановка задачи
Рассмотрим начальную задачу для уравнения следующего вида [3]:
du __ £(t)(u2 -a2)2
dt ( u 2 + a 2 )
с начальным условием u (0) = 0.
При ^ ( t ) = ^ 0 • cos t решение задачи (12)-(13) имеет вид:
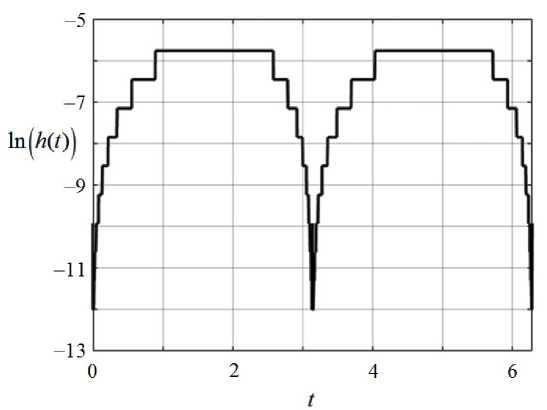
u 1 + ^/1 + 4 a ^E2( t) Z-(0)= Ую, t(0)= 0, i = 1, —,n. (11) где H(t) = ^osint. В дальнейших расчетах a = п. Жесткость задачи характеризуется множителем ^0 при периодической функции. Условно по значению параметра £0 можно разбить задачи вида (12)-(13) на следующие классы [5]: при малых значениях ^0 (порядка нескольких единиц) задача является нежесткой, при ξ0 ≥ 10 – жесткой и при ξ0 ≥ 1000 – сверхжесткой. Это определяется видом правой части: при приближении значения косинуса к нулю скорость изменения решения, даже при большом параметре £0, стремится к нулю, а при стремлении значения косинуса к единице значение правой части становится наибольшим. Таким образом, происходит смена плавно меняющихся компонент решения с быстро меняющимися переходными зонами, которые тем короче, чем больше значение ^0. Данные особенности видны на рис. 1. Явные методы решения Результаты решения задачи явным методом Эйлера и явным методом Рунге-Кутты четвертого порядка точности с постоянным шагом, схемы которых MORDOVIA UNIVERSITY BULLETIN даны выше, представлены на рис. 1 и в табл. 1. На рис. 1 изображены кривые, соответствующие решениям задачи (12)-(13) для значений ^0 = 1; 10; 100, полученные методом Рунге-Кутты четвертого порядка точности с постоянным шагом h = 0,001. Полученные численные решения визуально совпадают с аналитическими. Для явного метода Эйлера кривые аналогичны изображенным на рис. 1. В табл. 1 приведены данные о средней погрешности е, вычисленной с использованием аналитического решения (14), и времени счета tc решений задачи (12)-(13), полученных явными методами с постоянным шагом интегрирования. Из нее видно, что метод Рунге-Кутты четвертого порядка выигрывает у явного метода Эйлера в точности, хотя и требует большего времени счета. Стоит также отметить, что при повышении значения параметра $0 невозможно получить решение при малых шагах интегрирования. Так, для $0 = 10 невозможно получить решение при Р и с. 1. Численное решение задачи (12)-(13) при $0 = 1; 10; 100, метод Рунге-Кутты четвертого порядка с постоянным шагом h = 10-3 F i g. 1. Numeric solution of problem (12)-(13) for $0 = 1; 10; 100, fourth order Runge-Kutta method with constant step size h = 10-3 Т а б л и ц а 1 T a b l e 1 Погрешность решения и время счета для задачи (12)-(13), явные методы с постоянным шагом Computational error and computational time for problem (12)-(13), explicit methods with constant step size Здесь и далее расчет проведен на персональном компьютере с процессором DualCore Intel Core i5-660 3477 MHz, оперативной памятью 2,00 ГБ DDR3 SDRAM Kingston «ValueRAM» KVR1333D3N9/2G (2 шт.), видеокартой ATI Radeon HD 5770 (Juniper) 1,00 ГБ и 64-разрядной операционной системой Windows 10. Используемые методы реализованы в вычислительной среде Matlab R2012b. Замечание 3 В рассматриваемом диапазоне шагов интегрирования не удалось получить решение задачи (12)-(13) для $0 > 1 000. Анализируя полученные результаты, отметим, что для решения задачи с фиксированным $0 шаг интегрирования h не может превышать величину 1/$0. Это говорит о малоэффективности применения явных методов для решения сверхжестких задач при больших значениях $0. Неявный метод Эйлера Явные методы с постоянным шагом интегрирования позволяют получить ре-498 шение задачи (12)-(13) только при умеренных значениях $0. Уже при $0 = 103 в рассматриваемом диапазоне шагов интегрирования не удается найти решение. Можно ожидать, что неявные методы за счет расширения области устойчивости позволят получить решение при больших шагах интегрирования. Используем неявный метод Эйлера. На k-ом шаге решение задачи (12)-(13) неявным методом Эйлера находится как решение нелинейного уравнения вида: uk+1 = uk- h • £ocos(tk+1) ((uk+1 )2 -a2) (uk+1 )2+a2 . (15) Уравнение (15) решается методом простых итераций и методом Ньютона. Итерационный процесс метода простых итераций задается соотношением: uk +11) = uk — h • (j)\2 2 2 ^0cos(tk+1) ((uj ) — a ) (j ) uk +1 ) , а для метода Ньютона ‒ u (j+1) k+1 _ u (j) - F (tk+1, uk+1) k+1F4t u( j)) Fu(tk+1, uk+1) . В формуле (16) ^0cost (u2- a2) F (t, u) = u - uk + h------—— u2 + a2 FU( t, u) = 1- h • 2^0cost (u2- a2)u (u2+ 3a2) (u2 + a2 )2 dF (t, u) где F,'(t, u) = —^. du Кривые, полученные при решении задачи (12)-(13) неявным методом Эйлера, имеют вид, аналогичный представленному на рис. 1. В табл. 2 даны значения средней погрешности е и времени счета tc решений задачи (12)-(13), полученные неявным методом Эйлера с постоянным шагом интегрирования при использовании метода простых итераций и Ньютона. Расчеты показывают, что по сравнению с явным методом Эйлера неявный метод Эйлера позволяет получить результаты с меньшей погрешностью. Однако время счета в связи с усложнением вычислительного процесса как для метода простых итераций, так и метода Ньютона, может увеличиваться на порядок и более. При малой жесткости метод Ньютона позволяет быстрее получить решение задачи по сравнению с методом простых итераций, но с повышением жесткости уступает ему как в точности, так и в быстродействии. Это можно связать и с особенностями реализации метода Ньютона (в частности, с выбором начального приближения на каждом шаге) и с затруднением при переходе через внутренний слой для неявного метода Эйлера. Таким образом, используемый неявный метод не позволяет значительно улучшить результаты явных методов, затрачивая Т а б л и ц а 2 T a b l e 2 Погрешность решения и время счета для задачи (12)-(13), неявный метод Эйлера с постоянным шагом Computational error and computational time for problem (12)-(13), implicit Euler method with constant step size Наилучшая параметризация Из приведенных выше расчетных данных видно, что ни явные методы, ни неявный метод Эйлера не позволяют получить решение задачи (12)-(13) без значительных вычислительных затруднений. Применим к этой задаче метод продолжения решения по наилучшему аргументу35, описанный выше. Наилучший аргумент X для рассматриваемой задачи запишется в скалярном виде: dX1 = du2+ dt 2. (17) Преобразуя к аргументу (17) систему (12), получим: du dn dt d^ -§(t) (u2- a2)2 ( u2 + a2) + £2( t)( u2 - a2) ( u2+ a2) ( u2+ a2) + ^2( t)( u2- a2) Начальные условия (13) для системы (18) примут вид: u(0) = 0, t(0) = 0. (19) Как отмечалось выше, преобразованная задача (18)-(19) обладает рядом преимуществ при численном решении. В табл. 3 приведены результаты расчета преобразованной задачи (18)-(19) методом Рунге-Кутты четвертого по- рядка точности с постоянным шагом (качественно для метода Эйлера результаты аналогичны), где l – шаг по аргументу λ. Кривые, полученные при численном решении, аналогичны приведенным на рис. 1. Для сравнения в табл. 3 приведены результаты решения исходной задачи (12)-(13) с шагом, подбираемым из условия равенства порядков средней ошибки решения исходной и преобразованной задач. Видно, что для непреобразованной задачи (12)-(13) для достижения того же порядка ошибки приходится брать шаг до нескольких порядков меньше по сравнению с преобразованной. При этом, несмотря на то, что интервал изменения значений аргумента λ больше, чем у аргумента t, для задачи (18)-(19) удается сократить время счета от 0,4 (при ^0 = 1) до 10 раз (при $0 = 1 000). В табл. 4 приведены результаты расчета задач (12)-(13) и (18)-(19) методом Рунге-Кутты четвертого порядка с переменным шагом. Процедура изменения шага описана выше. Для преобразованной задачи (18)-(19) параметр точности для правила Рунге 9 = 10-12. Для исходной задачи (12)-(13) параметр 6 выбирался из условия равенства порядков средней погрешности для обеих задач. Результаты показывают, что и при переменном шаге интегрирования использование наилучшего аргумента X позволяет получить вычислительные преимущества: удается сократить время счета минимум в два раза. Для сверхжестких задач уменьшение времени счета может достигать нескольких порядков. Отметим также, что, в отличие от преобразованной задачи, решение исходной задачи зависит от начального шага; в особенности это характерно для больших значений $0. Однако стоит указать и на ряд недостатков наилучшей параметризации. Преобразованная задача (18)-(19) 34 Там же. Т а б л и ц а 3 T a b l e 3 Средняя ошибка и время счета задач (12)-(13) и (18)-(19), метод Рунге-Кутты четвертого порядка с постоянным шагом Computational error and computational time for problems (12)-(13) and (18)-(19), fourth order Runge-Kutta method with constant step size ξ0 Параметризованная задача / Parameterized problem Непараметризованная задача / Nonparametrized problem l ɛ tc, c h ɛ tc, c 1 0,1 5,4369∙10-7 0,0213 0,02 3,6307∙10-7 0,0418 0,01 2,9799∙10-11 0,183 0,002 3,6427∙10-11 0,2405 0,001 5,0522∙10-14 0,5505 0,0002 6,4592∙10-13 2,0987 10 0,1 2,4647∙10-4 0,0236 0,02 3,0375∙10-4 0,0422 0,01 3,2723∙10-9 0,0969 0,001 2,5136∙10-9 0,4414 0,001 3,7533∙10-12 0,5886 2∙10-4 3,662∙10-12 2,2979 100 0,1 0,3525 0,0289 0,004 0,0012 0,1303 0,01 4,834∙10-6 0,1178 0,001 2,4843∙10-6 0,4484 0,001 5,0063∙10-11 0,5289 5∙10-5 1,7076∙10-11 8,2501 1000 0,1 – – – – – 0,01 0,0047 0,2086 4,7∙10-4 0,0012 0,9134 0,001 4,0885∙10-8 0,5288 7∙10-5 5,9638∙10-8 5,9466 Т а б л и ц а 4 T a b l e 4 Средняя ошибка и время счета задач (12)-(13) и (18)-(19), метод Рунге-Кутты четвертого порядка с переменным шагом Computational error and computational time for problems (12)-(13) and (18)-(19), fourth order Runge-Kutta method with variable step size Еще одним недостатком является заниженная оценка погрешности по правилу Рунге для преобразованной задачи. Уже при $0 = 1 оценка погрешности на два порядка ниже, чем реальная средняя погрешность. Для сверхжестких задач разница возрастает до пяти порядков. Диаметрально противоположная ситуация характерна для исходной задачи. Здесь правило Рунге дает завышенную оценку погрешности начиная с $0 = 10. Если посмотреть на характер изменения шага интегрирования, изображенный на рис. 2 в полулогарифмических координатах, то видно, что уже при значении $0 = 30 значение шага интегрирования не поднимается выше 10-5, снижаясь до 10-12 в окрестности пограничных и внутреннего слоев. При этом значение шага изме- няется плавно, т. е. после прохождения внутреннего слоя шаг начинает плавно возрастать до максимального значения, а при подходе к внутреннему слою – плавно убывать до минимума (при этом ширина переходного слоя уменьшается при увеличении ξ0 ). Данный механизм изменения шага интегрирования и приводит к уменьшению погрешности решения на горизонтальных участках до значений меньших, чем задаваемая точность θ. Для преобразованной задачи кривая решения в зависимости от аргумента λ изменяется более плавно, как это отмечено в статьях А. А. Белова и Н. Н. Ка-литкина [3; 5]. По этой причине такого же падения погрешности не происходит; наоборот, в узловых точках, соответствующих внутренним слоям, концентрируется максимальная погрешность. В заключение отметим, что, исходя из характера изменения шага интегрирования, можно объяснить и увеличение времени счета для исходной задачи. Помимо усложнения процесса решения, связанного со сменой шага, уже при относительно малом значении $0 = 30 шаг Р и с. 2. Шаг интегрирования в полулогарифмических координатах для задачи (12)-(13) при $0 = 30, метод Рунге-Кутты четвертого порядка, 9 = 10-4 F i g. 2. Step size in semilogarithmic coordinates for problem (12)-(13), $0 = 30, fourth order Runge-Kutta method, 9 = 10-4 интегрирования не поднимается выше 10-5, при повышении же значения $0 шаг интегрирования будет уменьшаться еще сильнее, а вместе с этим будет возрастать время счета. Замечание 4 В отличие от непреобразованной задачи (12)-(13), переход к наилучшему аргументу позволяет получить хорошие результаты при параметре жесткости $0 большем, чем рассмотренные в табл. 3 и табл. 4. При задаваемой точности θ = 10-12 и начальном шаге h = 0,001 удается построить решение вплоть до $0 = 106. Замечание 5 Использование неявного метода Эйлера с переменным шагом не позволило получить результаты значительно лучшие, чем приведенные в табл. 2. Получить решение со средней погрешностью е порядка 10-2 удается, но время счета по сравнению с результатами табл. 2 возрастает до 10 раз при $0< 100. При большей точности (ɛ ≤ 10-3) или большей жесткости ($0 > 1000) результаты либо не удавалось получить, либо время счета составляло до 1 000 с. Обсуждение и заключение В статье рассмотрено применение традиционных явных и неявных методов решения задачи Коши с контрастными структурами. Получены численные решения задачи (12)-(13) с постоянным и переменным шагом, изменяемым по правилу Рунге. Анализируя результаты, приведенные на рис. 1 и в табл. 1‒2, отметим следующее. 1. Все полученные расчетные данные хорошо согласуются как с аналитическим решением, так и с результатами, полученными А. А. Беловым и Н. Н. Калиткиным [3; 5]. 2. При малых значениях параметра жесткости $0 явные методы с постоянным шагом позволяют получить решение с приемлемой погрешностью, но при больших $0 явные методы становятся малоэффективными, т. к. при фиксированном $0 шаг интегрирования 3. Используемый в статье неявный метод Эйлера дает возможность уменьшить погрешность полученного решения для малых $0, но не позволяет построить решение при $0 > 1 000. При этом, в силу особенностей реализации, время счета для неявного метода Эйлера значительно превышает аналогичные значения для явных методов. 4. Метод Ньютона, используемый при решении нелинейных уравнений в неявном методе Эйлера, при малых $0 позволяет сократить время счета по сравнению с методом простых итераций, но уступает ему в точности. 5. Неявный метод Эйлера вызывает значительные затруднения при переходе через внутренний слой, что сказывается на быстродействии и точности. h не может превосходить значения 1/$0. Уже при $0 > 1 000 решение в рассматриваемом диапазоне шагов интегрирования построить не удалось. Для устранения отмеченных недостатков исходная задача (12)-(13) преобразуется к наилучшему аргументу λ. Преобразованная задача (18)-(19) обладает рядом вычислительных преимуществ (см. табл. 3‒4). 1. При решении задачи (18)-(19) с постоянным шагом удается получить большую точность. При этом для исходной задачи, в зависимости от значения $0, аналогичные результаты можно получить с меньшим (от нескольких раз до нескольких порядков) шагом. Время счета для преобразованной задачи меньше от 0,4 (при $0 = 1) до 10 раз (при $0 = 1 000). 2. При использовании переменного шага интегрирования задача (18)-(19) также выигрывает в быстродействии. Переход к аргументу λ позволяет при одинаковых значениях средней погрешности сократить время счета от двух раз для малых значений $0 до нескольких порядков при $0 = 1 000. Более того, в отличие от исходной, преобразованную задачу можно решать вплоть до значений $0 = 106. 3. Для преобразованной задачи (18)-(19) процедура смены шага слабо зависит от начального шага 10, в то время как для исходной задачи решение существенно зависит от выбора начального шага h0. Помимо значительных преимуществ задача (18)-(19) имеет и ряд недостатков. 1. Правило Рунге для преобразованной задачи дает заниженную оценку локальной погрешности. Уже при $0 = 1 оценка погрешности на два порядка ниже, чем реальная средняя погрешность. Для сверхжестких задач разница возрастает до пяти порядков. Диаметрально противоположная ситуация отмечается с исходной задачей. Для нее правило Рунге дает завышенную оценку погрешности начиная с ξ = 10. Это необходимо учитывать при построении решения. 2. В отличие от исходного уравнения (12), преобразованная система (18) имеет большую размерность и усложненный вид. В ряде случаев это может Том 28, № 4. 2018 перекрывать преимущества наилучшей параметризации. Несмотря на отмеченные недостатки, наилучшая параметризация является одним из наиболее эффективных методов решения плохо обусловленных задач, к которым можно отнести и задачи с контрастными структурами. Показано, что традиционные явные и неявные методы имеют существенные ограничения в использовании при больших $0 и малоэффективны. В то же время переход к наилучшему аргументу позволяет получить решение рассматриваемой задачи даже при больших $0 быстро и с приемлемой точностью. В дальнейшем для подтверждения полученных результатов необходимо рассмотреть решение еще ряда тестовых и прикладных задач данного класса. Однако, опираясь на уже полученные результаты решения различных задач36-38 [33], можно предположить, что метод продолжения решения по наилучшему аргументу будет также эффективен и для других задач данного класса. Поступила 05.07.2018; принята к публикации 03.09.2018; опубликована онлайн 28.12.2018 Об авторах: Все авторы прочитали и одобрили окончательный вариант рукописи.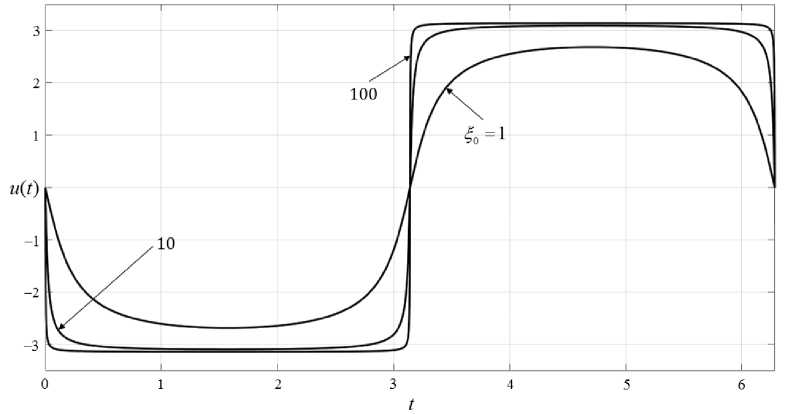
Параметры / Parameters
Явный метод Эйлера / Explicit Euler method
Метод Рунге-Кутты четвертого порядка / Fourth order Runge-Kutta method
$0
h
ɛ
tc, c
ɛ
tc, c
1
0,1
0,4548
0,009
2,1332∙10-4
0,0081
0,01
0,0361
0,0095
2,2776∙10-8
0,0656
0,001
0,0035
0,0255
2,1461∙10-12
0,1732
10
0,1
–
–
–
–
0,01
0,0826
0,0109
2,3893∙10-5
0,0168
0,001
0,008
0,0301
2,5136∙10-9
0,0759
100
0,1
–
–
–
–
0,01
–
–
–
–
0,001
0,0127
0,0381
2,4843∙10-6
0,1011
h = 0,1, а при $0 = 1 000 нельзя получить решение при h ≥ 10-3.
Параметры / Parameters
Неявный метод Эйлера / Implicit Euler method
Метод простой итерации / Fixed-point iteration method
Метод Ньютона / The Newton’s method
5о
h
ɛ
tc, c
ɛ
tc, c
1
0,1
0,3137
0,0662
0,3138
0,0255
0,01
0,034
0,1774
0,0345
0,1457
0,001
8,6629∙10-4
1,188
0,0035
0,6134
10
0,1
–
–
–
–
0,01
0,074
0,1864
0,0787
0,0878
0,001
0,0029
1,1653
0,008
0,7302
100
0,1
–
–
–
–
0,01
–
–
–
–
0,001
0,0078
0,9977
0,0126
1,5954
при этом большее время счета. Для повышения точности можно, как и в статье А. А. Белова и Н. Н. Калиткина «Численные методы решения задач Коши с контрастными структурами» [5], рекомендовать использование более сложных методов, например, неявных обратных схем Рунге-Кутты [37] или явно-неявных комплексных схем Розенброка [38].
Параметры / Parameters
Параметризованная задача / Parameterized problem
Непараметризованная задача / Nonparametrized problem
ξ0
h0 / l0
θ
ɛ
tc, c
θ
ɛ
tc, c
1
0,1
10-12
1,1561∙10-10
0,2388
10-10
2,1774∙10-10
0,4892
0,01
10-12
1,6079∙10-10
0,2592
3∙10-10
1,1338∙10-10
0,571
0,001
10-12
1,7008∙10-10
0,1889
10-10
2,1458∙10-12
1,3038
10
0,1
10-12
2,365∙10-9
0,2065
10-7
1,5164∙10-9
1,6533
0,01
10-12
2,2218∙10-9
0,2812
4∙10-8
1,1642∙10-9
2,025
0,001
10-12
1,6625∙10-9
0,2691
10-7
2,5134∙10-9
1,3089
100
0,1
10-12
3,497∙10-8
0,2982
10-4
5,8346∙10-8
3,2128
0,01
10-12
3,1933∙10-8
0,3346
10-5
2,3953∙10-8
4,0536
0,001
10-12
3,0792∙10-8
0,3015
3∙10-5
2,3106∙10-8
4,7691
1000
0,1
10-12
4,2953∙10-7
0,2729
–
–
–
0,01
10-12
3,2001∙10-7
0,2318
10-3
9,1802∙10-8
15,794
0,001
10-12
8,7845∙10-7
0,1772
10-2
6,4254∙10-7
9,8967
имеет более сложный вид и большую размерность по сравнению с исходной (12)-(13). Для рассматриваемой задачи это несущественно, но при решении задач большой размерности преимущества, даваемые наилучшей параметризацией, могут перекрываться сложностью преобразованной задачи.
Список литературы Параметризация задачи Коши для нелинейных дифференциальных уравнений с контрастными структурами
- Тихонов А. Н. О зависимости решений дифференциальных уравнений от малого параметра // Матемематический сборник. 1948. Т. 22 (64), № 2. С. 193-204. URL: http://mi.mathnet.ru/msb6075
- Васильева А. Б., Бутузов В. Ф., Нефедов Н. Н. Контрастные структуры в сингулярно возмущенных задачах // Фундаментальная и прикладная математика. 1998. Т. 4, № 3. С. 799-851. URL: http://mi.mathnet.ru/fpm344
- Belov A. A., Kalitkin N. N. Features of calculating contrast structures in the Cauchy problem // Mathematical Models and Computer Simulations. 2017. Vol. 9, Issue 3. P. 281-291. DOI: 10.1134/S2070048217030048
- Belov A. A., Kalitkin N. N. Curvature-based grid step selection for stiff Cauchy problems // Mathematical Models and Computer Simulations. 2017. Vol. 9, Issue 3. P. 305-317. X DOI: 10.1134/S207004821703005
- Белов А. А., Калиткин Н. Н. Численные методы решения задач Коши с контрастными структурами // Моделирование и анализ информационных систем. 2016. Т. 23, № 5. С. 529-538. DOI: 10.18255/1818-1015-2016-5-529-538
- Тихонов А. Н. О системах дифференциальных уравнений, содержащих параметры // Матемематический сборник. 1950. Т. 27 (69), № 1. С. 147-156. URL: http://mi.mathnet.ru/msb5907
- Тихонов А. Н. Системы дифференциальных уравнений, содержащие малые параметры при производных // Матемематический сборник. 1952. Т. 31 (73), № 3. С. 575-586. URL: http://mi.mathnet.ru/msb5548
- Butuzov V. F., Vasileva A. B., Nefedov N. N. Asymptotic theory of contrast structures (review) // Automatics and Remote Control. 1997. Vol. 58, Issue 7. P. 1068-1091. Available at: http://mi.mathnet.ru/at2615
- Butuzov V. F., Levashova N. T., Melnikova A. A. A steplike contrast structure in a singularly perturbed system of elliptic equations // Computational Mathematics and Mathematical Physics Journal. 2013; 53(9):1239-1259.
- DOI: 10.1134/S0965542513090054
- Бутузов В. Ф., Денисов И. В. Угловой пограничный слой в нелинейных эллиптических задачах, содержащих производные первого порядка // Моделирование и анализ информационных систем. 2014. Т. 21, № 1. С. 7-31. URL: http://mi.mathnet.ru/mais356
- Бутузов В. Ф., Белошапко В. А. Сингулярно возмущенная эллиптическая задача Дирихле с кратным корнем вырожденного уравнения // Моделирование и анализ информационных систем. 2016. Т. 23, № 5. С. 515-528.
- DOI: 10.18255/1818-1015-2016-5-515-528
- Butuzov V. F., Bychkov A. I. Asymptotics of the solution of the initial boundary value problem for a singularly perturbed parabolic equation in the case of a triple root of the degenerate equation // Computational Mathematics and Mathematical Physics Journal. 2016. Vol. 56, Issue 4. P. 593-611.
- DOI: 10.1134/S0965542516040060
- Бутузов В. Ф. О контрастных структурах с многозонным внутренним слоем // Моделирование и анализ информационных систем. 2017. Т. 24, № 3. С. 288-308.
- DOI: 10.18255/1818-1015-2017-3-288-308
- Козлов М. В., Щенников В. Н. Асимптотическая устойчивость однородных сингулярных систем // Вестник Мордовского университета. 2017. Т. 27, № 4. С. 546-554.
- DOI: 10.15507/0236-2910.027.201704.546-554
- Нефедов Н. Н., Никулин Е. И. Существование и асимптотическая устойчивость периодического решения с внутренним переходным слоем в задаче со слабой линейной адвекцией // Моделирование и анализ информационных систем. 2018. Т. 25, № 1. С. 125-132.
- DOI: 10.18255/1818-1015-2018-1-125-132
- Антипов Е. А., Левашова Н. Т., Нефедов Н. Н. Асимптотическое приближение решения уравнения реакция-диффузия-адвекция с нелинейным адвективным слагаемым // Моделирование и анализ информационных систем. 2018. Т. 25, № 1. С. 18-32.
- DOI: 10.18255/1818-1015-2018-1-18-32
- Давыдова М. А., Нефедов Н. Н. Существование и устойчивость контрастных структур в многомерных задачах реакция-диффузия-адвекция в случае сбалансированной нелинейности // Моделирование и анализ информационных систем. 2017. Т. 24, № 1. С. 31-38.
- DOI: 10.18255/1818-1015-2017-1-31-38
- Antipov E. A., Levashova N. T., Nefedov N. N. Asymptotics of the front motion in the reaction-diffusion-advection problem // Computational Mathematics and Mathematical Physics Journal. 2014. Vol. 54, Issue 10. P. 1536-1549.
- DOI: 10.1134/S0965542514100029
- Нефедов Н. Н. Общая схема асимптотического исследования устойчивых контрастных структур // Нелинейная динамика. 2010. Т. 6, № 1. С. 181-186. URL: http://mi.mathnet.ru/nd65
- Efstathiou C., Luhar M. Mean turbulence statistics in boundary layers over high-porosity foams // Journal of Fluid Mechanics. 2018. Vol. 841. P. 351-379.
- DOI: 10.1017/jfm.2018.57
- Comparison of turbulent boundary layers over smooth and rough surfaces up to high Reynolds numbers / D. T. Squire [et al.] // Journal of Fluid Mechanics. 2016. Vol. 795. P. 210-240.
- DOI: 10.1017/jfm.2016.196
- Swaters G. E. Internal dissipative boundary layers in the cross-equatorial flow of a grounded deep western boundary current // Geophysical & Astrophysical Fluid Dynamics. 2017. Vol. 111, no. 2. P. 91-114.
- DOI: 10.1080/03091929.2017.1287909
- Kumar D. A parameter-uniform method for singularly perturbed turning point problems exhibiting interior or twin boundary layers // International Journal of Computer Mathematics. 2018. P. 1-18.
- DOI: 10.1080/00207160.2018.1458098
- Xu H., Jin Y. L. The contrast structures for a class of singularly perturbed systems with heteroclinic orbits // Discrete Dynamics in Nature and Society. 2016. Article ID 6405853.
- DOI: 10.1155/2016/6405853
- Belov A. A., Kalitkin N. N., Kuzmina L. V. Modeling of chemical kinetics in gases // Mathematical Models and Computer Simulations. 2017. Vol. 9, Issue 1. P. 24-39.
- DOI: 10.1134/S2070048217010057
- Lahaye M. E. Une metode de resolution d'une categorie d'equations transcendentes // Comptes rendus hebdomadaires des seances de L'Academie des sciences. 1934. Vol. 198, no. 21. P. 1840-1842.
- Lahaye M. E. Solution of system of transcendental equations // Académie royale de Belgique. Bulletin de la Classe des sciences. 1948. Vol. 5. P. 805-822.
- Давиденко Д. Ф. Об одном новом методе численного решения систем нелинейных уравнений // Доклады Академии наук СССР. 1953. Т. 88, № 4. С. 601-602.
- Давиденко Д. Ф. О приближенном решении систем нелинейных уравнений // Украинский математический журнал. 1953. Т. 5, № 2. С. 196-206.
- Ворович И. И., Зипалова В. Ф. К решению нелинейных краевых задач теории упругости методом перехода к задаче Коши // Прикладная математика и механика. 1965. Т. 29, вып. 5. С. 894-901.
- Riks E. The application of Newton's method to the problem of elastic stability // Journal of Applied Mechanics. 1972; Vol. 39, Issue 4. P. 1060-1065. URL: http://appliedmechanics.asmedigitalcollection.asme.org/article.aspx?articleid=1400638
- Kuznetsov E. B., Leonov S. S. Parametrization of the Cauchy problem for systems of ordinary differential equations with limiting singular points // Computational Mathematics and Mathematical Physics Journal. 2017. Vol. 57, Issue 6. P. 931-952.
- DOI: 10.1134/S0965542517060094
- Кузнецов Е. Б., Леонов С. С. Примеры параметризации задачи Коши для систем обыкновенных дифференциальных уравнений с предельными особыми точками // Журнал вычислительной математики и математической физики. 2018. Т. 58, № 6. С. 914-933.
- DOI: 10.7868/S0044466918060066
- Semenov A. A. Strength and stability of geometrically nonlinear orthotropic shell structures // Thin-Walled Structures. 2016. Vol. 106. P. 428-436.
- DOI: 10.1016/j.tws.2016.05.018
- May S., Vignollet J., de Borst R. A new arc-length control method based on the rates of the internal and the dissipated energy // Engineering Computations. 2016. Vol. 33, Issue 1. P. 100-115.
- DOI: 10.1108/EC-02-2015-0044
- A local pseudo arc-length method for hyperbolic conservation laws / X.Wang [et al.] // Acta Mechanica Sinica. 2015. Vol. 30, no. 6. P. 956-965.
- DOI: 10.1007/s10409-014-0091-0
- Kalitkin N. N., Poshivaylo I. P. Computations with inverse Runge-Kutta schemes // Mathematical Models and Computer Simulations. 2014. Vol. 6, Issue 3. P. 272-285.
- DOI: 10.1134/S2070048214030077
- Rosenbrock H. H. Some general implicit processes for the numerical solution of differential equations // The Computer Journal. 1963. Vol. 5, no. 4. P. 329-330.
- DOI: 10.1093/comjnl/5.4.329


