Парето-оптимизация производственного расписания на основе метода муравьиных колоний

В работе рассматривается задача многокритериальной оптимизации производственного расписания с помощью муравьиного алгоритма (МА) с адаптивными весами. Присущие МА свойства способствуют их эффективному применению при решении задач многокритериальной оптимизации, так как МА используют множество потенциальных решений – популяцию и глобальный поиск в нескольких направлениях [1-3]. Кроме этого, МА не предъявляют требований к виду целевых функций и ограничений. МА хорошо показали себя для решения за- дач комбинаторной оптимизации, одной из которых является задача составления производственных расписаний технологического оборудования гибких производственных систем (ГПС) автоматизированного технологического комплекса (АТК) механообработки [4, 5]. Известны применения МА при решении задач как комбинаторной [6], так и численной [7] оптимизации.

Для оценки качества потенциальных решений в процессе поиска решений на основе МА используются объектно-ориентированные модели, которые описывают важнейшие характеристики систем и позволяют с приемлемой достоверностью проводить моделирование их функционирования. Многокритериальная оптимизация получила широкое применение при решении различных задач [8-10].

• 1    Производственное расписание

Задача синтеза расписания работы ГПС заключается в том, чтобы для производственного участка с заданным технологическим маршрутом составить порядок обработки деталей, учитывая ограничения реальных производственных ситуаций за данное время. Модель такого процесса удобно представить в виде ориентированного графа, построение которого эквивалентно определению чисел t ij - моментов начала технологической операции O ij . В статье совокупность чисел {t ij } (i = 1,2..., n; j = 1, 2..., m i ), удовлетворяющая производственным условиям, называется расписанием работы ГПС или его графовой моделью G(i), где i - тип детали, п- количество деталей, j- технологическая операция, m - количество технологических операций [1, 4, 5].

В МА каждый искусственный муравей находит своё потенциальное решение, концентрация искусственного феромона определяется качеством построенного решения в соответствии с используемыми формулами коррекции концентрации феромона. Важнейшими компонентами МА являются правила (и соответствующие формулы расчёта вероятностей) для выбора следующей вершины графа в процессе поиска решения, которые определяют последовательность рассмотрения потенциальных решений. Для адаптации МА к решению поставленной задачи необходимо выполнить следующую последовательность действий.

• 1)    разработать схему представления потенциального решения.

• 2)    определить правила коррекции концентрации искусственного феромона, учитывающие качество потенциального решения.

• 3)    разработать глобальные эвристики для определения выбора дуги при поиске пути в графе.

• 4)    определить локальную эвристику поведения муравья в виде вероятности перехода при построении решения.

• 5)    определить инструмент проверки выполнимости потенциального решения с учётом ограничений задачи.

• 6)    проверить адекватность модели.

• 2    Графоаналитическая модель

На основе разработанной графоаналитической модели (см. рисунок 1) построена объектно-ориентированная модель организационно-технологического процесса загрузки оборудования, которая представляет систему взаимодействующих классов её типовых компонентов. Эта модель описывает структуру классов, составляющих систему производственного процесса, их атрибуты, операции, взаимосвязи с другими классами.

В раб о те [1] рассмотрено п остроени е графоан а литическ о й модели G=(V, D, P ) , где V -множеств о вершин, каждая из которых п редставл я ет позици ю обработ к и детале й ; D - множество д у г графа, представля ю щих вре м я перехода от одно й технолог и ческой о п ерации на другую; P - матрица правил п е рехода, гд е каждой д уге (i, j) g D приписы в ается вес P j .

Пред с тавленная на рисун к е 1 графо а налитиче с кая модел ь предусм а тривает распределение обор у дования по техноло г ическим о перациям согласно п лану вып у ска детал е й, а также позволяе т варьировать его ко л ичеством, в зависим о сти от ис п равности оборудов а ния и плановых пр о филактических рабо т .

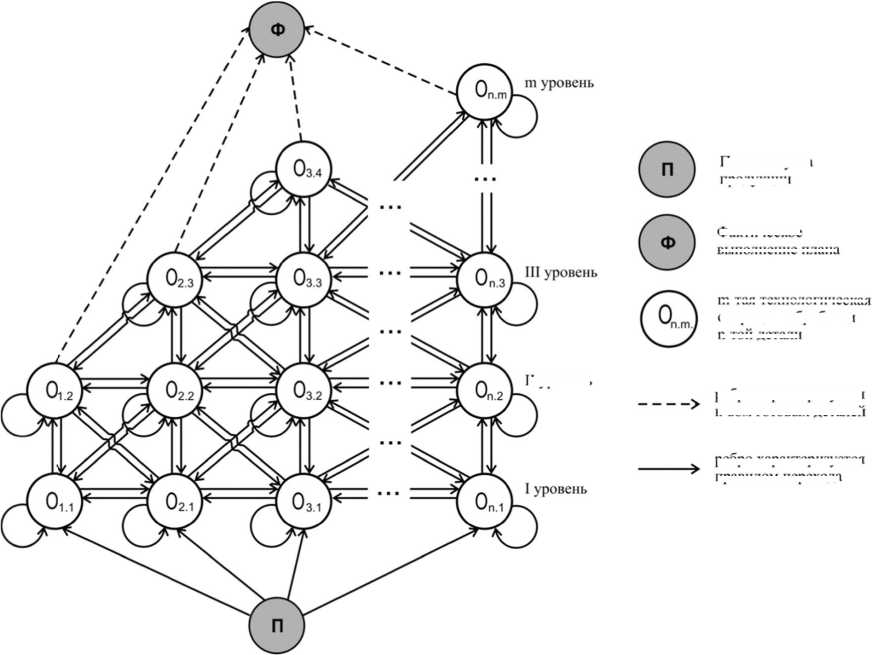
II уровень реоро характеризуется к-вом готовых детален

План выпуска продукции рсоро характеризуется правилом перехода m-тая технологическая операция обработки п-тои дет.in

Фактическое выполнение плана

Р исунок 1 - Графоаналит и ческая мод е ль организа ц ионно-техн о логическог о процесса загр у зки гибких п роизводств е нных модул е й

Исхо д ная вершина графа о пределяе т начало в ы полнени я плана пр о изводств а (согласно производ с твенной программе и техноло г ическим картам изг о товления д еталей) - стартовую точку, ко т орая характеризуетс я следующими параметрами:

• (1)                       П = (Kv, D, N p l i , Od i , Rd i , Ts i ),

где Kv - к оличество гибких п р оизводст в енных мо д улей (ГП М ) на про и зводствен н ом участке;

D - обще е количество деталей d i по прои з водствен н ой програ м ме;

Npl_t -коли ч ество деталей i -того типа по п р оизводст в енной про г рамме;

Od i - кол и чество операций O ij , для изгот о вления де т али i-того типа;

Rd i - раз м ер партии запуска де т алей i -то г о типа;

Ts i - срок изготовления парти и деталей i - того типа.

Оста л ьные вершины гра ф а разбиты на уровн и , каждый из котор ы х соотве т ствует отдельной т ехнологической опе р ации O ij ( согласно т ехнологи ч еской кар т е). Кажд а я вершина O ij одноз н ачно определяется п а раметрам и :

• (2)                              O ij = (N ij , n ij , Тv ij , Tn ij , Тпр ij , L1 ij , L2 ij L3 ij ),

где N ij – номер ГПМ, на котором выполняется операция O ij ;

n ij – количество запущенных в обработку деталей d i ;

Tv ij – время выполнения технологической операции O ij ;

Tn ij – время наладки ГПМ для выполнения операции O ij ;

Tпр ij – время простоя ГПМ перед выполнением операции O ij ;

L1 ij – объём свободного места в лотке для заготовок;

L2 ij – объём свободного места в лотке для готовой продукции;

L3 ij – объём свободного места в лотке для инструментов.

Правило перехода ГПМ из стартовой точки в вершины первого уровня не является случайным событием, а рассчитывается с использованием временных параметров технологических карт изготовления деталей и с учетом сроков выполнения заказа:

K ij

• (3)     P ij = z K j , 2 P ij = ¹

где K ij –коэффициент перехода:

Toij *kf

• (4)    ^{K =} Is

m ,

• (5)    To .j = S ^Tn .j + ^Tv .j *n ., - j = 1

где Tо ij – время выполнения операции O ij над партией деталей i -того типа;

kf – коэффициент возможности перехода.

(6)                        TSi = ki*dl, где ki – количество рабочих дней для выполнения заказа; dl – длительность рабочей смены, ч.

Время освобождения ГПМ из вершины рассчитывается с учётом величины максимальной партии запуска и временных параметров выполнения технологических операций:

(7)                       T с в ij = Ly*Tvy + Tnlj + ТпPij, где Lij – максимально допустимая партия запуска деталей di.

• 3    Направленный муравьиный алгоритм

Для оптимизации расписания производственного участка АТК предложен «направленный» МА, для которого: 1) разработана схема представления потенциального решения; 2) определены правила коррекции концентрации искусственного феромона, которые определяют положительную обратную связь; 3) разработана эвристика выбора дуги при поиске пути в графе; 4) определено «направленно-пропорциональное» правило перехода в следующую вершину графа; 5) выбраны «глобальные правила» для расчёта концентрации искусственного феромона, которые способствуют направленному поиску; 6) разработаны объектные модели для проверки выполнимости потенциального решения с учётом ограничений задачи; 7) произведена проверка адекватности предложенной модели.

Преимуществом разработанного алгоритма является то, что он не требует построения структурной модели самого производственного участка и допускает простые модификации, которые позволяют эффективно решать оптимизационные задачи подобного класса. Эта модификация отличается от [3] следующими особенностями:

• 1)    Предложен метод вычисления вероятностей перехода искусственного муравья по вершинам графоаналитической модели, основанный на анализе текущей производственной ситуации; вероятность перехода k-того муравья в вершину O ij определяется соотношением

[ τ ij (t)] ^α ⋅ [ η ij (t)] ^β P_ij,k(t) =    _l

O ij ∈ N i^kj

O ij ∉ N i^kj

ЖГ [nij(t)]e k=1

Pij,k(t) =0, где α – коэффициент, определяющий степень влияния феромона; β – коэффициент, определяющий влияние эвристической информации; τij – концентрация феромона на дуге графа; nij - эвристическая информация (обычно, длина дуги); N-j - перечень вершин графа Oj, доступных для k-того муравья, t – номер итерации в процессе поиска решения.

• 2)    Предпочтительность выбора вершины графа задаётся «направленно-пропорциональным» правилом перехода между вершинами, основанным на эвристической информации. Она определяется отношением времени выполнения технологической операции To ij к запланированному времени изготовления детали Ts i , которое в свою очередь корректируется после выполнения каждой технологической операции над партией деталей

To ij

• (9)    η ij ⁼ Ts .

• 3)    Для расчёта концентрации искусственного феромона при переходе муравья на следующий узел графа используются «глобальные» правила, которые способствуют направленному поиску. Эти правила заставляют муравьи двигаться в сторону найденных «худших» решений с целью их «улучшения». Такая стратегия стимулирует эксплуатацию пространства поиска и применяется после того, как решение построено, т.е. после прохождения всеми муравьями своего пути. В этом случае концентрацию феромона разрешается корректировать только «худшим» муравьям, построившим неоптимальный путь. Тогда для каждой дуги графа концентрация феромона корректируется в соответствии с правилом

nk

Tij (t +1) = Tj (t) + kTy (t), ATj (t) = 2 A T (t), k =1

где Δ τ - количество искусственного феромона, откладываемое муравьями, определяется в зависимости от заданного критерия оптимальности и вычисляется по одному из следующих правил:

• •    для задачи максимизации среднего коэффициента загрузки оборудования

(11)                        Δ τ _ij (t) = _k ,

A T nP ij i,j где Τnpkij – время простоя k-го оборудования перед выполнением операции Οij;

• •    для задачи минимизации времени переналадок оборудования

  
  

  Δ τ i^kj (t) =

  
  

AN, i,j где Tnkij – время наладки ГПМ для выполнения операции Oij на k-ом оборудовании;

• •    для задачи минимизации длительности цикла изготовления деталей

  
  

  А т j (t) =

  
  

2 Tnpk + Tok , i,j где Toij – времени выполнения технологической операции Oij на k-ом оборудовании.

• 4 Парето-оптимизация производственного расписания на основе «направленного» муравьиного алгоритма

При использовании метода взвешенной функции для решения задач многокритериальной оптимизации «общая» целевая функция F(x) строится из целевых функций f(x) в виде их взвешенной суммы

q

• (14)                  F ( x ) = 2 wf ( x ).

i = 1

Каждой целевой функции f (x) присваивается свой вес w , и задача сводится к скалярному случаю. При этом различные веса w дают разные решения в смысле Парето. Скалярное значение общей целевой функции вычисляется путём суммирования взвешенных значений q критериев оптимальности. Для параллельного поиска кратных решений веса не фиксируются, что даёт возможность «направленному» МА расширять фронт по всем направлениям.

В предложенном алгоритме на каждой итерации по определённому критерию оптимизации формируется множество решений на основе «направленного» МА. Далее для исследуемых решений определяются максимальная и минимальная экстремальные точки в пространстве заданных критериев (Z). В итоге получаем гиперплоскость, которая определяется двумя экстремальными точками, и содержит все текущие решения, показанные на рисунке 2. Указанные две экстремальные точки обновляются на каждой итерации. При этом адаптивный вес k -ой цели определяется соотношением

• ⁽¹⁵⁾                     w_k =---- ¹—-, k = 1,2,...,q.

k max min

• z k ^- z k

Для каждой цели на основе выбранных критериев эффективности устанавливаются средневзвешенные весовые коэффициенты значимости, которые нормируются внутри группы.

норм. wk wk --- i=1

^q ∑ ^w

k = 1,2,

q.

Тогда на каждой итерации взвешенная целевая функция определяется согласно следующему выражению

q

• (17)                     z(x) = 2 w H^0PM. (f k (x) - z mⁱⁿ ).

k = 1

Вначале алгоритма предполагается инициализация - обнуление всех значений Zm n и Zmax . Поскольку экстремальные точки обновляются на каждой итерации, то соответственно обновляются и веса.

В течение процесса поиска решения в пространстве z каждой популяцией муравьев адаптивная гиперплоскость последовательно приближается к положительной (или отрицательной) идеальной точке (см. рисунок 2).

Поскольку для каждого из критериев оптимальности может быть задана своя точность решения, которая достигается при различных количествах итераций n t , для их определения проведены экспериментальные исследования всех однокритериальных задач и определено количество итераций, при котором будет достигнута точность, соответствующая технологическим условиям. В качестве критерия останова при решении многокритериальной задачи выбирается максимальное значение количества итераций, полученной из решения однокритериальных задач.

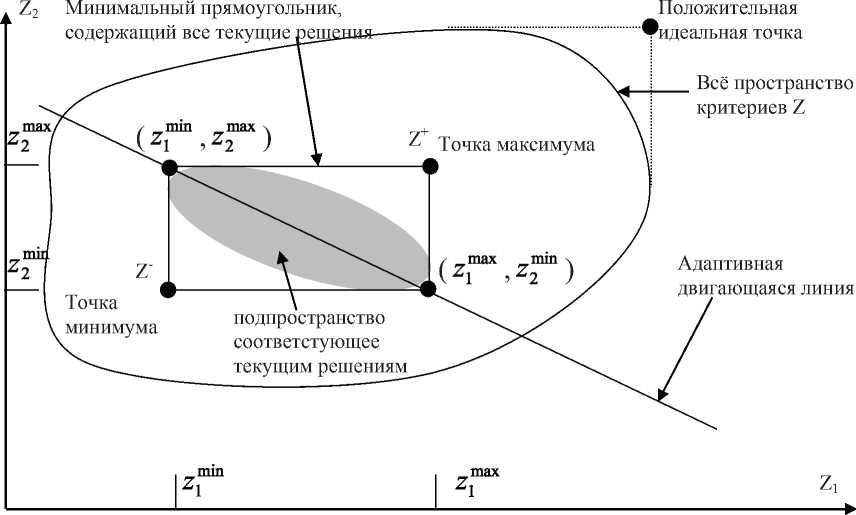
Рисунок 2 - Адаптивные веса и адаптивная гиперплоскость

Таким образом, описанный выше метод многокритериальной оптимизации позволяет перебирать всё пространство решений для каждой популяции муравьёв и выбирать из них пути, оптимальные в смысле Парето.

• 5 Экспериментальные исследования

В ходе эксперимента на объектной модели АТК решены многокритериальные задачи с применением «направленного» МА с адаптивными весами. Анализ результатов проводился по сравнению с решениями, полученными при решении однокритериальной задачи. Рассмотрим следующие варианты выбора критериев оптимальности.

• I.    Максимизация среднего коэффициента загрузки технологического оборудования.

• II.    Минимизация нарушения крайних сроков изготовления заказа при минимальной длительности цикла изготовления деталей.

• III.    Минимизация нарушения крайних сроков изготовления заказа при минимизации времени переналадок оборудования.

• IV.    Минимизация нарушения крайних сроков изготовления заказа при минимальной длительности изготовления деталей и времени переналадок оборудования.

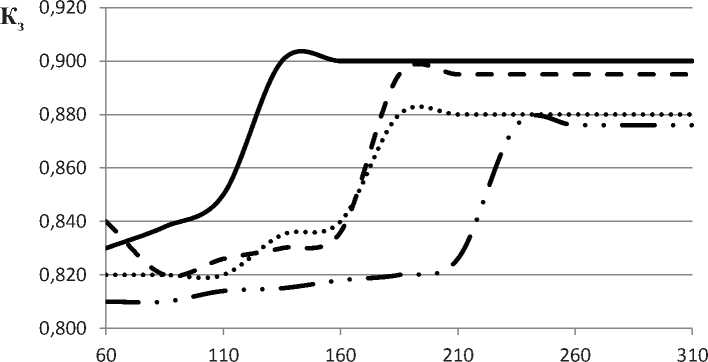
Для проведения анализа полученных решений были рассмотрены зависимость среднего коэффициента загрузки технологического оборудования (Кзср) и времени нарушения крайних сроков заказа (Тср) в зависимости от количества популяций муравьев nt для каждого из вари- антов выбора критериев оптимальности. Отметим, что максимизация Кзср включает в себя и минимизацию производственного цикла и настроек оборудования одновременно. Полученные результаты представлены на рисунках 3 и 4 соответственно.

Анализ полученных результатов показывает, что предложенный «направленный» МА с адаптивными весами для многокритериальной задачи требует большего количества итераций, чем подобный алгоритм для однокритериальной задачи. Причём с увеличением числа критериев увеличивается количество популяций муравьев для нахождения Парето-оптимального решения. Так, для однокритериальной задачи (I вариант) количество итераций, необходимое для достижения субоптимального решения, n t = 140, для двухкритериальных задач (II и III варианты) n t = 190, а для трёхкритериальной задачи (IV вариант) n t = 240. Однако если предоставить «направленному» МА данное количество ресурса n t , он неизменно показывает свою эффективность и позволяет получить «хорошие» решения.

nt

-I

■ II

• III

•IV

Рисунок 3 – Зависимость среднего коэффициента загрузки оборудования от количества итераций для различных вариантов выбора критериев оптимальности

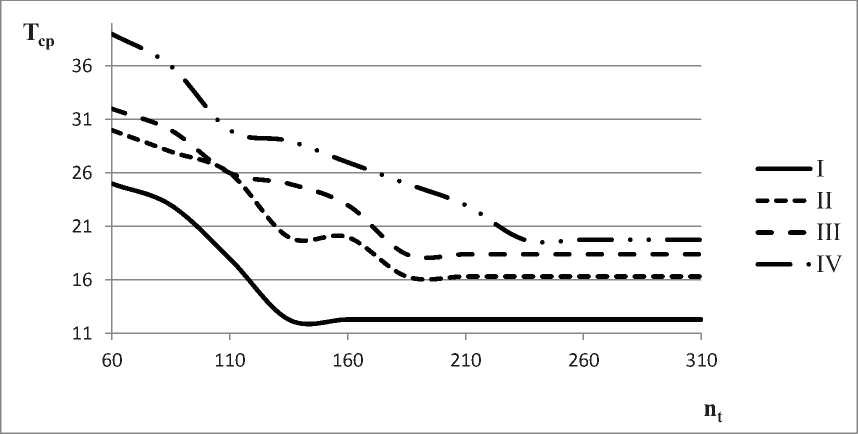
Рисунок 4 – Зависимость времени нарушения крайних сроков изготовления заказа от количества итераций для различных вариантов выбора критериев оптимальности

Заключение

Проведённые исследования основных временных параметров, полученных в результате решения задачи оптимизации производственного расписания, показали, что при введении дополнительных критериев эффективности задача выбора оптимальных решений значительно усложняется, однако эффективность методов существенно не снижается. Так, на рисунке 5 представлены диаграммы, отражающие разницу между значениями основных параметров, полученных путём однокритериальной и многокритериальной оптимизаций.

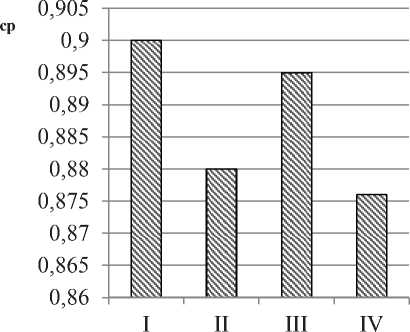
а) средний коэффициент загрузки

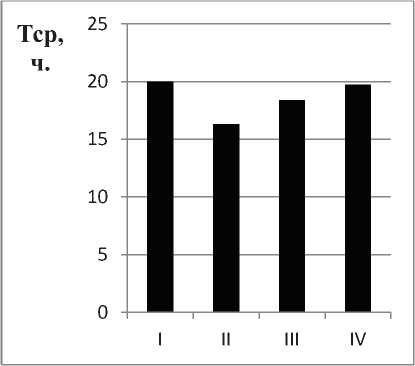
б) время нарушения крайних сроков

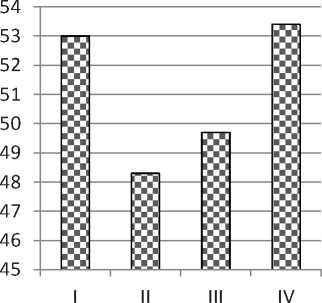
в) время наладки оборудования

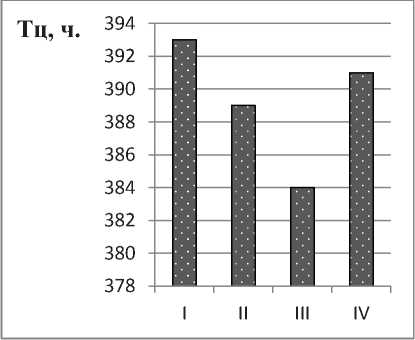
г) длительность производственного цикла

Рисунок 5 – Значения среднего коэффициента загрузки оборудования и временных параметров, полученных в результате оптимизации производственного расписания, в зависимости от варианта выбора критериев эффективности

Таким образом, можно сделать вывод о том, что применение метода Парето-оптимизации производственного расписания АТК на основе «направленного» МА с адаптивными весами для многокритериальной задачи позволяет получать результаты, в наименьшей степени отличающиеся от решения однокритериальной задачи. Т.е. при оптимизации одновременно по нескольким критериям, качество полученных решений по каждому критерию в отдельности значительно не снижается, что говорит о выборе верной тактики решения подобных задач.