Passenger body vibration control in active quarter car model using hybrid ANFIS PID controller

Published Online May 2018 in MECS

Suspension system performs multiple tasks in vehicle body related to control of generated vibrations from road irregularities to provide good passenger ride comfort as well as road holding capability by keeping continuous wheel contact with varying road surface profiles. An automotive suspension design engineer has to build the suspension system parts such as to deliver compromising results among various conflicting requirements in terms of passenger ride comfort, road holding ability and load carrying capability. A traditional passive suspension system is uncontrolled type and works on the combination of spring and damper system having fixed stiffness and damping characteristics. Such passive system provides limited suspension performance in certain frequency range. To achieve the desired conflicting tasks in vehicles, automotive manufacturers have developed semi-active and active suspension system based technology. Generally, a semi-active suspension is assembled with magneto-rheological or electro-rheological dampers, generating variable damping force in suspension system of vehicle [1-2]. An active suspension system is highly successful in achieving the desired tasks compared to passive and semi-active one. Such type of suspension system are able to suppress the passenger seat, sprung mass and unsprung mass vibrations as well as to minimize suspension deflection effectively in a wider frequency range. Active suspension system assembly contains various mechatronics based devices such as actuators and sensors in combination with a spring and damper. The assembled sensors receive the signals from the vibrating suspension structure. These signals are transferred to the assembled controllers, which supply required amount of damping force using controllable actuators in suspension system. Therefore, active suspension systems are top choice for automotive developers and researchers due to attractive characteristics of providing high ride comfort during accelerating and braking conditions as well as best road holding ability during running period [3-5].

• II.    Related Work

In order to achieve desired ride comfort and vehicle handling issues, various control approaches based on fuzzy logic control, PID control, neural network control and ANFIS control etc. have been proposed. The vibration suppression results of sprung mass, unsprung mass and suspension system depends and varies based on various developed and implemented control strategies. Huang and Lian [6] designed a hybrid control scheme based on the combination of fuzzy control and neural network control. Rao and Prahlad [7] used a tunable fuzzy controller in suspension system of active quarter car model. Kuo and Li [8] proposed genetic-algorithm optimized fuzzy proportional- plus-integral/proportional-plus-derivative controller in automotive active suspension system. Sharkawy [9] implemented a fuzzy and adaptive fuzzy control in active suspension system to achieve two different criteria related to road holding and vehicle ride comfort. Mouleeswaran [10] showed the improved performance of PID controller in active quarter car model related to the passenger ride comfort and vehicle handling issues compared to passive one through simulation results. Salem and Aly [11] presented the vehicle handling and ride comfort simulation results in active quarter car model using fuzzy and PID control. Yildirim and Eski [12] proposed neural network control to achieve high ride quality in non-linear experimental active quarter car model. Lin and Lian [13] developed a hybrid selforganizing fuzzy controller and radial basis function neural network controller for application in active suspension system. Li et al. [14] designed a reliable fuzzy H∞ controller to demonstrate its effectiveness in active suspension system of quarter car model considering the vibration performance of sprung and unsprung mass and suspension deflection performance. Kothandaraman and Ponnusamy [15] obtained the training data set based on the LQR controller results for designing Adaptive Neuro Fuzzy Controller (ANFIS). The parameters of ANFIS controller were tuned using Particle Swarm Optimization technique. Lin et al. [16] implemented a linear switched reluctance actuator with proportional-derivative (PD) control in active quarter car model. Heidari and Homaei [17] used back propagation neural network technique to determine the gain parameters of a PID controller. The designed neural network based PID controller successfully achieved lower vibration values of suspension parameters in active quarter car model. Rosli et al. [18] implemented a hybrid control in active suspension of quarter car model using Active Force Control with Iterative Learning and proportional-integral derivative control strategy. Emam [19] developed a fuzzy self-tuning mechanism to achieve the gain parameters of PID controller in active quarter car model. Fard and Samadi [20] trained the adaptive neuro fuzzy controller (ANFIS) using the database of fuzzy, LQR and sliding mode controller. The designed ANFIS controller showed the better performance in terms of reduced quarter car body and suspension vibrations compared to passive, fuzzy and LQR based active suspension systems. Kalaivani et al. [21] used neural network controller and showed its effectiveness in vibration control of suspension parameters. Devdutt and Aggarwal [22] designed a hybrid fuzzy – PID controller with coupled rules for application in active quarter car model. Simulation results showed the better performance of designed HFPIDCR controller in achieving high performance for passenger ride comfort and safety. Recently, various control strategies such as interval fuzzy controller [23], optimal law [24], robust sampled data H∞ control [25], finite frequency H∞ control [26], composite nonlinear feedback control [27], fuzzy sliding mode control [28], active force control [29], LQR control [30], multi-objective control [31] and continuous and discrete sliding mode control [32] etc. have been used and compared for suppression of road induced vibrations in active quarter car suspension system.

It can be seen from the above literature that the design, development and implementation of proper controller plays a crucial role in vibration control in active quarter car model. In order to achieve enhanced performance of controllers, combination of advantages of two or more control approaches have been considered in recent years. Several research work has shown the acceptable level of ride comfort and vehicle handling issues using hybrid control strategy compared to single controller results [3334]. Furthermore, various studies were devoted to the improvement of passenger ride comfort in active quarter car model with three degrees of freedom [35-36].

In this study, a nonlinear active quarter car model with hybrid ANFIS PID controller approach is used for improving passenger ride comfort. To achieve an improved and enhanced passenger ride comfort, an active quarter car model with four degrees of freedom is considered. For this purpose, a hybrid ANFIS PID controller is developed and applied in primary suspension system of nonlinear quarter car model with four degrees of freedom. This hybrid ANFIS PID controller combines the advantages of both ANFIS and PID controller. Simulation work is carried out in time and frequency domain for passenger ride quality comparison.

The remaining paper is organized in various sections as follows. Section III describes the active quarter car model with four degrees of freedom. Section IV presents the design of various ANFIS and PID based controllers. Section V shows the simulation work and results. Section VI and VII contains power spectral density analysis and frequency domain analysis. Finally, section VIII and IX presents the robustness analysis and conclusion work respectively based on the research work results.

• III.    Active Quarter Car Model with Passenger Body

A quarter car model having seat suspension along with main suspension has been successfully used to study the passengers ride comfort and vehicle response against the uneven road surface induced vibrations. Seat suspension plays a vital role in controlling passenger seat vibrations in vehicle system during driving conditions thus helpful in improving the health and safety of travelling passengers. A quarter car model is the simplest car model compared to half car and full car model and provides the vehicle performance results taking only vertical motion into account while vehicle roll and pitch motions are ignored. Here, passive and active quarter car models with four degrees of freedom are considered for investigating the passenger body dynamic performance as well as control effort required to achieve the desired results. The active quarter car model is advanced stage of traditional passive quarter car model obtained by integrating additional controllers in it. The selected active quarter car model for study purpose is presented in Fig. 1 in which m1 , m2 , m3 and m4  are passenger body mass, passenger seat mass, sprung mass and unsprung mass respectively; k1, k2 and k3 are stiffness of seat cushion, seat suspension and main suspension respectively; c1, c2 and c3 are damper damping coefficients of seat cushion, seat suspension and main suspension respectively whereas kt represents the tire stiffness. The dynamic equations of this active quarter car model are as follows:

mi_zY + сг(?г - ±2) + k1( Z1 - Z2) = 0(1)

^m2^Z2 + ^C2^(Z2 ^{- Z}3 ) + ^k 2 ( ^z 2 - ^z 3 ) ^{- C}1^(Z1 ^{- Z} 2 )

-kM - z2) = 0(2)

m₃Z₃ + c₃⁽Z₃ - Z4) + k₃⁽Z₃ - Z4)- C 2 ⁽Z 2 - Z 3 )

-k2( Z2- Z3) + Fa = 0(3)

Rule i: If e is A, and de is Bt then ft = p,e + q,de + r, where the total number of rules are represented as i = 1, 2, 3, .... 25. A and B are fuzzy linguistic membership sets for two inputs e and de whereas the crisp output provided by ANFIS controller is ft. The output is dependent on the consequent parameters { pt, qt, r,}.

m 4 Z 4 - C 3 ⁽Z 3 - Z4) - k 3⁽ Z 3 - Z4) + k_t⁽Z 4 - Z_r)

- F_a = 0                  (4)

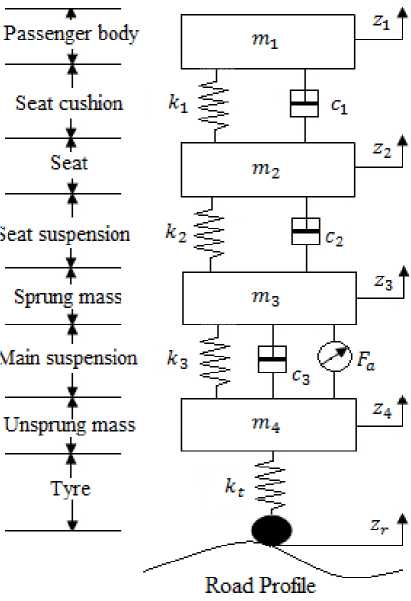
Fig.1. Active quarter car model with passenger body

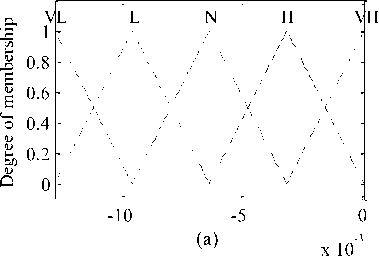
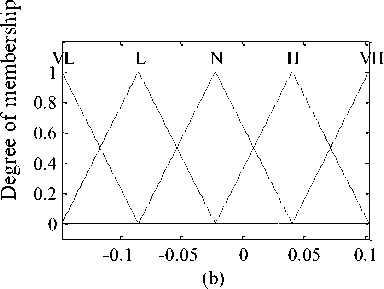
Fig.2. Membership functions for (a) error signal, e (b) derivative of error signal, de

• IV.    Controller Design

In this research work, the aim of proposed controllers is vibration control of human body in active quarter car model to achieve best ride comfort of travelling passengers. ANFIS and HANFISPID controllers are developed for application in suspension system of active quarter car model.

• A.    ANFIS Controller

The designed ANFIS controller has two crisp inputs as e (error) and de (change of error). The inputs e and de are represented by five linguistic terms, such as VL: Very Low, L: Low, N: Normal, H: High and VH: Very High respectively. Each input is having five linguistic terms resulting into the formation of total 5x5 = 25 rules. The first order Takagi-Sugeno fuzzy model is used in ANFIS controller design. The general if-then rule responsible for generating damping force is written in the following equation:

z

1,000

-1000

-2500 0.1

0 de       -0.1

-10

-5 e

-3 x 10

Fig.3. Input/ output ANFIS surface plot

The data set with 170 rows was selected for training between two inputs and one output. The number of epochs for training purpose was 50. The number of traingular membership functions for two inputs e and de was 5, each resulting into a total 25 (5x5=25) number of rules. The designed ANFIS model was trained using combination of back-propagation gradient descent method and least-square method. The optimized triangular shaped membership functions after training for two inputs are shown in Fig. 2. The generated surface plot based on the designed ANFIS controller is shown in Fig. 3.

• B. . Hybrid ANFIS PID Controller

Proportional–Integral–Derivative (PID) controller is widely used in mechatronics based industries due to its design simplicity and effectiveness. A PID controller is also known as a three-term controller and follows the input reference signal. It combines proportional, integral and derivative of the difference in reference signal position and current position of signal supplied from controlled system.

The output signal, U PI D(t) generated by PID controller is based on the following law:

t

U pid ( t ) = K p e ( t ) + K i X e ( t ) + K D e ( t )       (5)

i = 0

where e(t) is the error signal defined as e(t) = y_re ^ — y, while y_Tef is the reference position and y is the current position whereas K_P , K_I and K_D are proportional, integral and derivative gains respectively. The structure of Hybrid ANFIS PID (HANFISPID) controller combines the effectiveness of ANFIS and PID controllers as shown in Fig. 4.

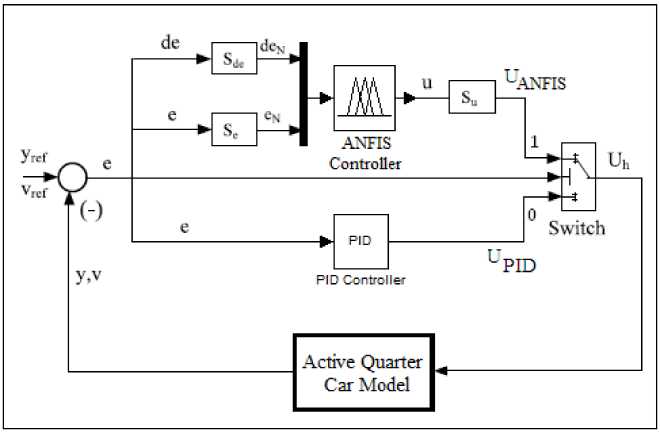
Fig.4. HANFISPID controller in active quarter car model

• V.    Simualtion Work and Results

0.05 0.5 3.5

In this section, simulation work is performed based on the developed simulink models of passive and active quarter car models with four degrees of freedom using simulink package. For simulation work, the vehicle speed and simulation time was set as 40 km/hr and 4 seconds respectively. The selected mathematical values of the quarter car model for simulation studies are given in Appendix A. Passenger ride quality and vehicle controlling performance is affected by the smoothness as well as roughness of road surface profile because transmitted vertical vibrations depend on tire and road contact forces. The selected random road excitation is shown in Fig. 5. The performance comparison of passive and active quarter car models is done with ANFIS and HANFISPID controllers in time and frequency domain. The passenger body response in terms of acceleration and displacement response are considered. The excitation response of passenger body is shown in Fig. 6. It can be observed that active suspension with HANFISPID controller generated best vibration suppression response related to acceleration and displacement response of passenger body compared to other controlled and passive suspension system.

1.5        2       2.5

Time (sec)

-0.05 0

Fig.5. Random road profile

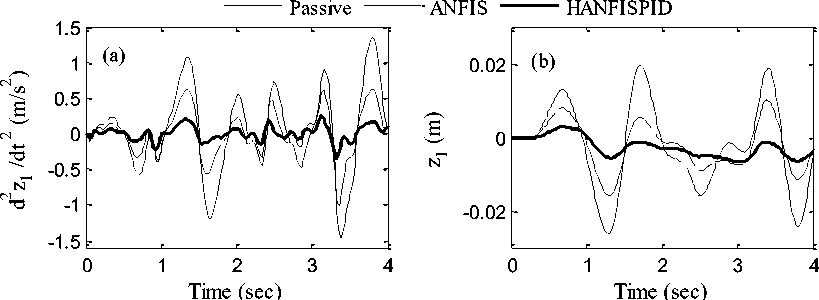
Fig.6. Passenger body response (a) acceleration (b) displacement

Simulation results of passenger body response in mathematical values are presented in Table 1 taking peak and root mean square (RMS) values of acceleration and displacement response as two criteria. It can be seen that the best response is delivered by HANFISPID controlled suspension system compared to other cases in terms of vibration suppression of passenger body.

Time histories of supplied damping forces in suspension system as well as power consumed by ANFIS and HANFISPID controllers are shown in Fig. 7 and Fig. 8 respectively. Higher control force is delivered by HANFISPID controller as well more power is consumed by this controller compared to ANFIS controller. Table 2 indicates that the IAE, ITAE, ISE and ITSE values are lower for HANFISPID controller compared to ANFIS based controller and passive suspension system. It shows the effectiveness of HANFISPID controller in vibration control of vehicles parts compared to other cases.

Table 1. Simulation results of passenger body under random road profile

Measurement	Criterion	Controller Type
		Passive	ANFIS	HANFISPID
Acceleration (m/s2)	Peak	1.3403	0.6310 (-52.92%)	0.2446 (-81.75%)
	RMS	0.5651	0.3121(-44.77%)	0.1025 (-81.86%)
Displacement (m)	Peak	0.0195	0.0101 (-48.21%)	0.0029 (-85.13%)
	RMS	0.0112	0.0064 (-42.86%)	0.0037 (-66.96%)

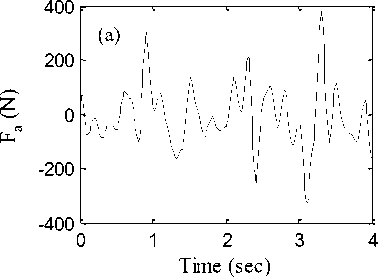
Fig.7. (a) Damping force supplied by ANFIS controller (b) Power consumed by ANFIS controller

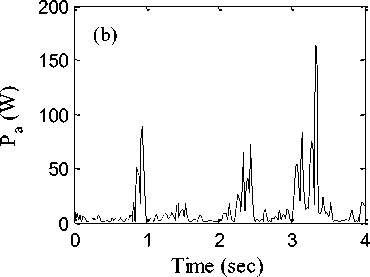
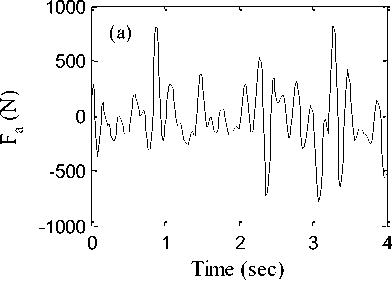
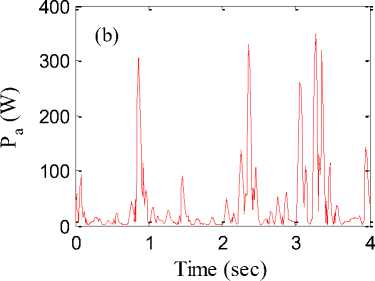
Fig.8. (a) Damping force supplied by HANFISPID controller (b) Power consumed by HANFISPID controller

Table 2. Controller response for passenger body under random road profile

Controller Type	Performance
	IAE	ITAE	ISE	ITSE
Passive	0.0462	8.76E-04	0.1068	1.71E-03
ANFIS	0.0335	4.60E-04	0.0762	9.25E-04
HANFISPID	0.0264	2.93E-04	0.0585	5.85E-04

• VI.    Spectral Density Analysis

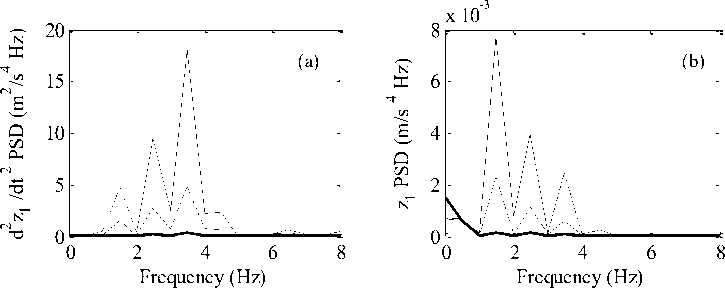
Power spectral density (PSD) signals were calculated from time domain data of passenger body acceleration and displacement response and represented in frequency domain. The power spectral densities of the passenger body for controlled and passive cases in terms of acceleration and displacement results for random road profile are shown in Fig. 9. As expected, the PSD magnitude response of passenger body acceleration and displacement are considerably reduced for HANFISPID controlled suspension system in frequency domain compared to other two considered cases. Thus, HANFISPID controller results in PSD analysis for passenger body response also confirm the superior performance in rejection of road induced disturbances.

Passive        ANFIS

HANFISPID

Fig.9. PSD response of passenger body (a) acceleration (b) displacement

• VII.    Frequency Domain Analysis

In this section, the frequency characteristics in the bode magnitude plots of the designed passive and active suspension system are compared and the results are represented. The performance analysis of passenger ride comfort in frequency domain is done by taking transfer function from the road to the passenger body acceleration as well as displacement response. The graphical results obtained through simulation work in bode plots are used to compare the open loop and closed loop performance of passenger ride comfort. Fig. 10 shows the passive and active quarter car response in log-magnitude bode plots of acceleration and displacement response. The main performance criterion viz. passenger body comfort is mainly assessed using these plots.

The passive quarter car model with 4 degrees of freedom shows peaks at four frequencies in the bode plots corresponding to the natural frequencies of passenger body (0.8695 Hz), passenger seat (1.4295 Hz), sprung mass (4.5996 Hz) and unsprung mass (11.2610 Hz) respectively. In order to improve the ride comfort, it is important to isolate the vehicle body from the road disturbances and to decrease the resonance peak of the passenger body mass around 1 Hz which is known to be a sensitive frequency to the human body.

We can see that the peak magnitude of passenger body response is reduced in case of active suspension system having ANFIS and HANFISPID controller near resonance frequency. This represents the better suppression of road disturbances at this frequency values for active quarter car models. However, HANFISPID controlled suspension system proves most effective at passenger body natural frequency compared to passive and ANFIS controlled suspension system. The gain at the natural frequency of passenger body in this case is considerably lower compared to other two cases.

Here, ANFIS and HANFISPID controller damps the natural frequencies of passenger body, passenger seat and sprung mass respectively but the performance of unsprung mass has degraded in active quarter car model. The peak magnitude at the natural frequency of unsprung mass has increased in both controlled cases compared to passive one. Such degradation in performance of unsprung mass in frequency domain can be attributed to the tire stiffness in the active suspension system since integrated controller has no control over this parameter.

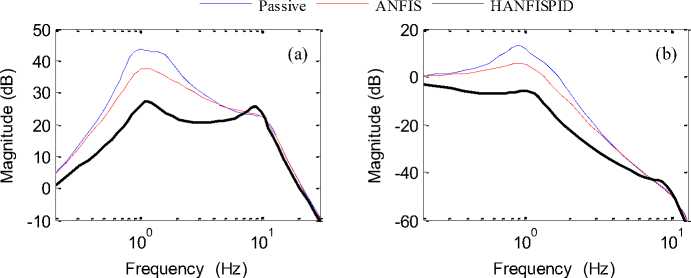
Fig.10. Bode plot (a) Passenger body acceleration (b) Passenger body displacement

• VIII.    Robustness Analysis

Since HANFISPID controller can successfully provide best performance for passenger ride comfort in bode plots of acceleration and displacement cases. Thus the robustness analysis is carried out for active quarter car model with HANFISPID controller in frequency domain to provide a reliable, robust system against model uncertainties and external disturbances as well as acceptable performance for different loading and working conditions. The effect of variation in sprung mass (m3), damper damping values (c3) and primary suspension spring stiffness (k3) values are studied in frequency region to observe its effect on passenger body vibrations in active quarter car model. The robustness results of considered cases taking frequency domain analysis is evaluated and shown in separate diagrams. The various values selected for the sprung mass variation, damping variation and primary suspension stiffness variation are shown in Table 3 with nominal values and the range of variations in each case.

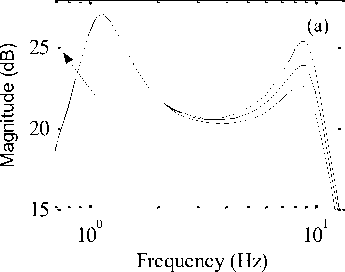
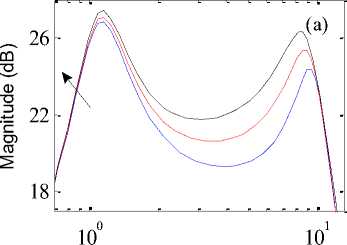
Fig.11. Bode plot for sprung mass variation (a) Passenger body acceleration (b) Passenger body displacement. The arrow head shows the direction of mass variation

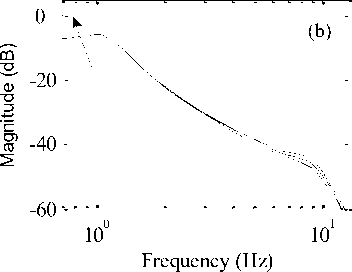
Frequency (Hz)

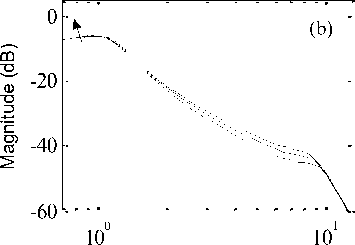
Fig.12. Bode plot for damper damping variation (a) Passenger body acceleration (b) Passenger body displacement. The arrow head shows the direction of damper damping variation

Frequency (Hz)

Table 3. Variation of quarter car parameters

Parameter	Nominal Value	Variation
Sprung mass (m3)	325 kg	± 50 kg
Damper damping (c3)	1550 N/m/s	± 300 N/m/s
Spring stiffness (k3)	20000 N/m	± 4000 N/m

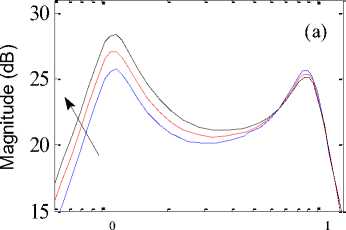
Frequency (Hz)

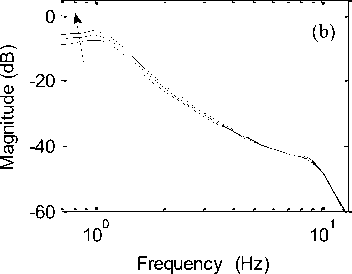
Fig.13. Bode plot for spring stiffness variation (a) Passenger body acceleration (b) Passenger body displacement. The arrow head shows the direction of spring stiffness variation

In present case, different sprung mass values (275 kg, 325 kg and 375 kg) were selected to observe the effect of sprung mass variation on the passenger body ride comfort in active suspension system. The influence of damper damping variation were considered on the passenger body response with different damper damping (1250 N/m/s, 1550 N/m/s and 1850 N/m/s) values. While the spring stiffness values were varied (16000 N/m, 20000 N/m and 24000 N/m) to study its influence on passenger body ride comfort. The arrow head direction shown in Fig. 11 to Fig. 13 represents the influence of passenger mass variation, damper damping variation and spring stiffness variation on the ride comfort of passenger body. It can be seen from Fig. 11 to Fig. 13 that the response in terms of natural frequency of passenger body acceleration and displacement magnitude increases with increase in sprung mass values, damper damping values and spring stiffness values respectively.

Finally, it can be seen that the stability of the active quarter car system with HANFISPID controller is robust to sprung mass variations, damper damping variations and spring stiffness variations in frequency region. The peak magnitude in natural frequency region changes with respect to these parameter variations as shown in magnitude-bode plots of each figure. But the overall performance resulted in low magnitude in natural frequency region using HANFISPID controller in active suspension system compared to passive and ANFIS controlled suspension cases. Thus, despite the variations in magnitude of the parameters, the active suspension with HANFISPID control system provided good stability and little variations in magnitude values. This shows that the system with HANFISPID controller provided stability and robustness against the changes of the quarter car parameters values.

• IX.    Conclusions

This paper considered a hybrid control design strategy taking ANFIS and PID controller. The problem related to passenger body ride comfort analysis was presented by a rigorous and detailed performance study in time and frequency domain taking passive and active quarter car results. The designed ANFIS and HANFISPID controllers were used in active quarter car models. The simulation results of quarter car model with four degrees of freedom were presented under random road excitations in graphical response and mathematical values. The HANFISPID controller provided maximum vibration suppression of passenger body in acceleration and displacement response under considered road excitation. HANFISPID controller also generated smaller IAE, ITAE, ISE and ITSE values in active quarter car model compared to passive and ANFIS controller cases. The robustness analysis of active suspension system with HANFISPID controller was presented taking variations in sprung mass, damper damping and spring stiffness values. Simulation results showed the best performance of HANFISPID controlled model in robustness criterion also. Consequently, based on the above discussion, it can be finalized that HANFISPID controller is best choice for application in active suspension system for achieving desired values of passenger body ride comfort and safety in travelling vehicles.

Appendix A

Parameter values of the quarter car model with passenger body

Mass parameters (kg)	Stiffness parameters (N/m)	Damping parameters (Ns/m)
т 1 = 75	к 1 = 8350	с 1 = 150
m 2 = 18	к2 = 7550	с2 = 850
m3 = 325	к3= 20000	с3 = 1550
т4 = 40	kt =180000