Пассивная идентификация объектов управления средствами toolbox Ident

Достаточно часто провести активный эксперимент для идентификации объекта автоматического управления не представляется возможным с точки зрения нарушения при этом технологического процесса и технологической безопасности.

Поэтому в некоторых случаях более приемлема пассивная идентификация. Под пассивной идентификацией понимается, что есть выборка значений сигнала на входе объекта и на выходе объекта. По данным сигналам необходимо идентифицировать объект.

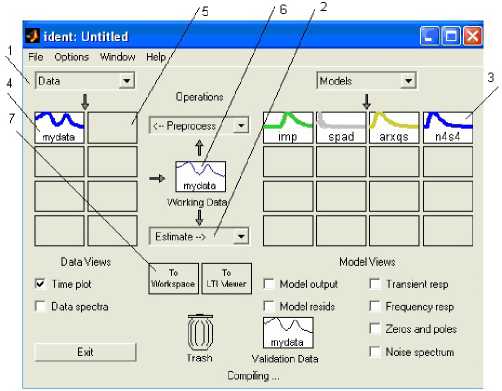
Пассивная идентификация осуществляется с помощью toolbox ident . Открыть toolbox можно, набрав в командной строке MATLAB слова ident , В результате откроется окно, приведенное на рисунке 1.

Рассмотрим конкретный пример идентификации объекта управления. Для этого в simulink соберем модель, приведенную на рисунке 2.

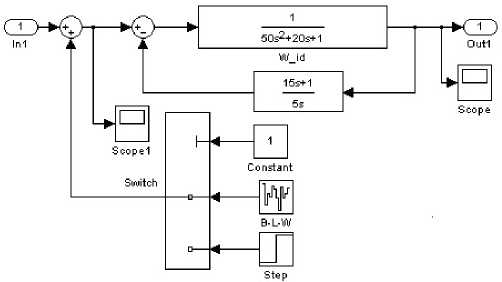
Рис. 2. Модель системы управления

Передаточная функция объекта на рисунке 2 имеет вид:

Wb(s) =--------

50s* +205+1

Эту передаточную функцию нам и необходимо получить в результате идентификации. Передаточная функция ПИ-регулятора с настроечными параметрами Kp =3 и Ti =5

имеет вид:

„ / ч 15s+1

5s

Настроечные параметры регулятора и его структура нам должны быть известны. Блоки Switch , Constant , B-L-W и Step необходимы для формирования различных тесто-

Установим в блоке Constant значение, равное двум, что эквивалентно подаче на вход объекта единичного скачка. Запустим модель и получим график выходного сигнала, приведенный на рисунке 3.

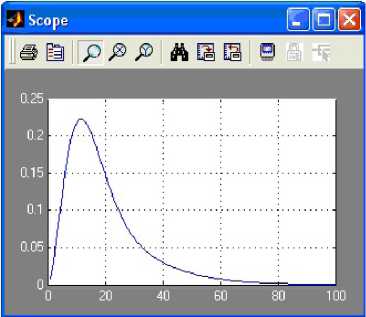
Рис. 3. График переходного процесса системы

Такой график мы должны будем получить после идентификации нашей системы. Но сразу отметим, что это график переходного процесса в замкнутой системе управления, а конечной нашей целью является получение передаточной функции объекта.

Теперь установим в блоке Constant значение, равное единице, что эквивалентно подаче на вход объекта случайного сигнала.

График случайного сигнала на входе объекта приведен на рисунке 4.

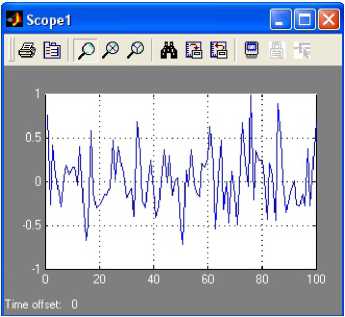
Рис. 4. График случайного сигнала на входе объекта SysX

Блоки Scope необходимо настроить соответствующим образом, как показано на рисунке 5.

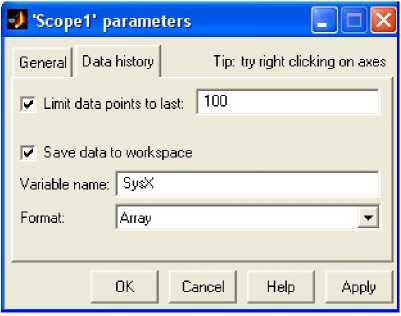
Рис. 5. Настройки блока Scope

Это необходимо, чтобы в рабочей среде MATLAB получить массивы входного и выходного сигналов. В нашем случае идентификатором входного сигнала является SysX, а идентификатором выходного сигнала SysY. График выходного сигнала приведен на рисунке 6.

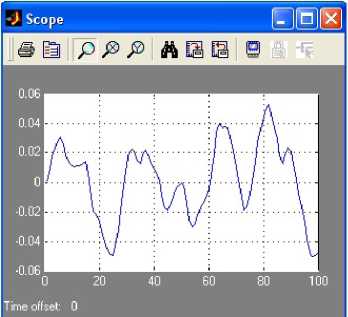
Рис. 6. График сигнала на выходе объекта SysY

Необходимо отметить, что сигналы SysX и SysY передаются в рабочую среду MATLAB в виде матриц, первый столбец которых является вектором времени, а для системы Ident необходимы вектора только самих сигналов. Для исключения векторов времени выполним в рабочем окне MATLAB команды:

SysX=SysX(1:100,2)

SysY=SysY(1:100,2)

Теперь у нас есть все, для проведения идентификации. При практической идентификации сигналы SysX и SysY можно ввести в рабочее окно MATLAB вручную, либо импортировать их из трендов сначала в Excel , а затем в MATLAB. Модель необходима для проверки точности идентификации.

Для загрузки данных в пакет Ident необходимо в раскрывающемся списке Data (п. 1 на рис.1) выбрать опцию « Import ». В результате откроется окно, приведенное на рисунке 7.

Нажимаем на кнопку « Import ». В результате произойдет загрузка данных, о чем свидетельствует появление графика в позиции 4 на рисунке 1.

Посмотреть графики импортированных данных можно, нажав флажок « Time plot ».

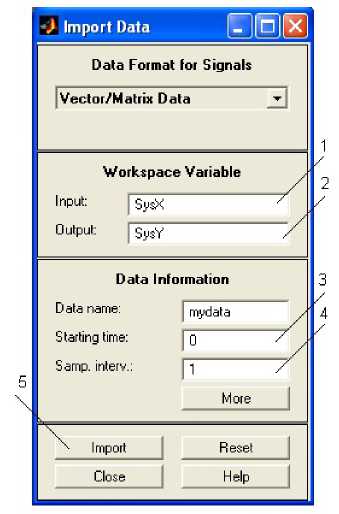
Рис. 7. Окно Import Data

Для запуска идентификации в раскрывающемся списке « Working Data » (п. 2 на рис. 1) выбираем команду « QuickStart ». В результате осуществляется идентификация четырьмя способами, о чем свидетельствует четыре графика (п. 3 на рис. 1).

Необходимо отметить, что блок Ident имеет множество способов идентификации и настроек, но описать все это в пределах одной статьи не представляется возможным. В нашем случае нас интересует идентификация модели в пространстве состояний, описываемая уравнениями:

x(t+Ts) = A x(t) + B u(t) + K e(t) y(t) = C x(t) + D u(t) + e(t)

Такой модели соответствует график n 4 s 4 (п. 3 на рис. 1). Имя графика может отличаться, в зависимости от используемых настроек и порядка рассчитанной модели.

Кликнем правой кнопкой мыши по указанному графику. В результате откроется окно, приведенное на рисунке 8.

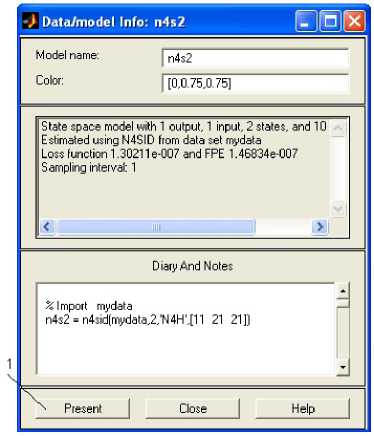
Рис. 8. Окно Data / model Info

Нажимаем кнопку Present (п.1. на рис. 8). В результате в командном окне MATLAB получаем матрицы модели в пространстве состояний под именем ans .

	- 0,684	-0,08	0,088		- 0,261 ”
л =	-0,157	1,018	0,163	в =	0,053
	-0,250	-0,226	0,907		-0,0008

C = [0,049 -0,078 -0,180]

В результате в командном окне MATLAB получаем матрицы модели в пространстве состояний под именем графика, в нашем случае под именем n4s4.

Выполним в командном окне:

>>W=tf(ans)

В результате получим передаточные функции модели по разным входам:

Transfer function from, input «u1» to output «y1»

0.00087 z5 -0.00109z-0.0076

z3 -2.603 z2 +2.277z- 0.6703

Transfer function from input «v@y1» to output «y1»

0.0002 z3 -0.00034 z2+0.00017z-3.94e-005 z3-2.603z2 + 2.777 z-0.6703

Нас интересует первая передаточная функция, поэтому выполним:

W1=W(1)

Как видно из приведенных выше формул мы получили передаточную функцию в дискретной форме.

Для преобразования ее в аналоговую форму, выполним команду:

W2=d2c(W1)

В результате получим передаточную функцию:

-3.148e-008 sz+0.02s-7.5e-018 № 2(j) =-----;-------;------------------ j3 + 0.4s2+0.08s+0.004

Сократим полученную передаточную функцию, выполнив команду:

Wz=mineral(W2)

В результате получим передаточную функцию замкнутой системы по возмущению:

-3.148e-008 s2+0.02s

И z(j) = -;------ч------------- ? + 0.4j²+0.08s+0.004

Чтобы построить график, выполним команду:

step(Wz),grid

В результате получим график, приведенный на рисунке 9.

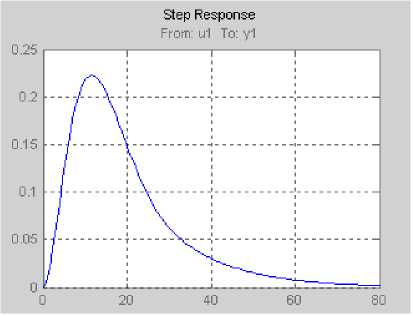
Рис. 9. График переходного процесса в замкнутой системе

Если сравнить графики, приведенные на рисунках 3 и 7, то мы видим, что они выглядят абсолютно идентично. Но как было сказано ранее, нас интересует не передаточная функция замкнутой системы, а передаточная функция объекта управления. Для этого необходимо исключить из полученной передаточной функции замкнутой системы передаточную функцию регулятора.

Из теории автоматического управления известно, что передаточная функция замкнутой системы имеет вид:

№(s) =----------- №b(j)^(i) + l

Отсюда передаточная функция объекта будет определяться по формуле:

x -№(5) WbtsA =------------

№(s)RX$)-l

Также известно, что передаточная функция ПИ-регулятора с раздельными настройками является параллельным соединением усилительного и интегрирующего звеньев. Чтобы получить ее в MATLAB, выполним последовательность команд:

Kp=tf([3],[1]);

Ti=tf([1],[5 0]);

Wp=Kp+Ti

В результате получим:

1 ISs+l И№)=—-

Для получения передаточной функции объекта, выполним в командном окне MATLAB:

Wo=-Wz/(Wz*Wp-1)

Сразу сократим полученную передаточную функцию, выполнив команду:

Woa=minreal(Wo)

В результате, получим передаточную функцию объекта:

,      3.14e-0.008s2+0.02s ffaatj) = -,-------,--------------------

J + 0.4s + 0.025 + 3.675 — 10

Чтобы проверить адекватность полученной передаточной функции исходной, а в нашем примере она нам известна, введем ее в командном окне MATLAB:

Wo=tf([1],[50 20 1])

Построим графики двух передаточных функций в одно окне, выполнив команду:

step(Wo,Woa,100),grid

В результате получим графики, приведенные на рисунке 10.

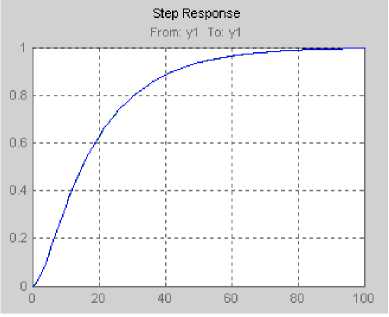
Рис. 10. Графики исходной и аппроксимированной передаточной функции

И в самом деле, если отбросить бесконечно малые величины в передаточной функции Woa(s) и сократить чис- литель и знаменатель на оператор Лапласа s, то получим передаточную функцию:

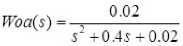
Остается только умножить числитель и знаменатель на коэффициент 50, чтобы получить искомую передаточную функции.

Итак, можно сделать вывод, что, используя пассивную идентификацию можно получить достаточно точные результаты в случаях, когда провести активный эксперимент по каким-либо причинам невозможно. Естественно, что точность на реальных объектах будет зависеть и от наличия дополнительных возмущающих воздействий, и о точности передачи сигналов из формируемых трендов в рабочую среду MATLAB.

Вторая особенность такой идентификации заключается в том, что должна быть известна структура и настроечные параметры используемого в системе регулятора. Это тоже не всегда просто получить, особенно при использовании нестандартных регуляторов, реализованных на микропроцессорных контроллерах в виде программного кода.