Перенос геомагнитного поля в магнитосферный хвост

Диссипативные процессы в магнитосферной плазме, в частности аномальное сопротивление плазмы, существенным образом влияют на характеристики процессов, протекающих в магнитосфере Земли [Ли-перовский, Пудовкин, 1983]. В [Китаев, 1996а] показано, что размеры дневного каспа и электрическое поле в каспе при нулевом ММП определяются эффективной проводимостью плазмы на магнитопаузе. Перенос геомагнитного поля на ночную сторону течением плазмы в плазменном слое и формирование магнитосферного хвоста также зависят от проводимости плазмы. Если бы условие вмороженности магнитного поля в плазменном слое было выполнено, то это привело бы к постоянству магнитного потока в долях хвоста при небольшом уменьшении величины магнитного поля в хвосте с расстоянием от Земли. В случае низкой проводимости плазмы конвективный перенос геомагнитного поля на ночную сторону был бы несущественен и диполеобразное магнитное поле быстро убывало бы при удалении от Земли. Очевидно, что магнитное поле магнитосферного хвоста формируется как результат конвективного переноса геомагнитного поля и диффузии магнитного поля в плазменном слое. В настоящей работе исследуется влияние проводимости плазмы в плазменном слое на конфигурацию магнитного поля в дальнем магнитосферном хвосте.

В работах с использованием глобального МГД-мо-делирования [Raeder, et al., 1995; 1996] уже рассматривалось влияние параметров солнечного ветра на крупномасштабную структуру магнитосферного хвоста. В частности, в [Raeder, et al., 1996] показано, что на процессы в плазменном слое сильно влияют значения вязкости и проводимости плазмы, задаваемые в модели. Метод глобального МГД-моде-лирования достаточно хорошо передает крупномасштабную структуру магнитосферы, однако ему свойственны ограничения в описании некоторых количественных соотношений [Pulkkinen, et al., 1995]. Одна их причин, наряду с рассмотренными в [Pulkki-nen, et al., 1995], это присутствие так называемых суточных вязкости и проводимости, кроме вязкости и проводимости среды, явно задаваемых в модели. Это хорошо известное свойство конечно-разностных методов решения дифференциальных уравнений. Не останавливаясь подробно на анализе указанных составляющих вязкости и проводимости, следует отметить, что при решении трехмерной задачи взаимодействия солнечного ветра с геомагнитным полем их достаточно трудно контролировать. По указанным причинам оправданно создание более простых моделей процессов в магнитосфере, в которых нет ограничений на задаваемые параметры, диктуемые сложностью задачи.

Ниже рассматривается стационарная модель переноса геомагнитного поля в хвост течением плазмы в плазменном слое. В модели геометрия плазменного слоя и долей хвоста считается заданной, а скорость течения в плазменном слое также считается известной и задается на основе данных спутниковых измерений. Это ощутимо упрощает проблему и сводит ее к решению линейной задачи по определению магнитного поля в области заданной конфигурации.

Двумерная модель переноса магнитного поля в магнитосферном хвосте

Геометрические параметры модели приведены на рис. 1. Доли хвоста представлены областями постоянной ширины, равной L 0 = 25 R E . Плазменный слой также имеет постоянную толщину D = 4 R E .

Рассматривается двумерная модель, поэтому скорость течения в плазменном слое имеет только x -компоненту u . Зависимость скорости от координаты x задана на основе данных ISEE-3 [Slavin, et al., 1985]. Согласно [Slavin, et al., 1985], на расстояниях 100 R E и более от Земли течение практически всегда

А . В . Китаев

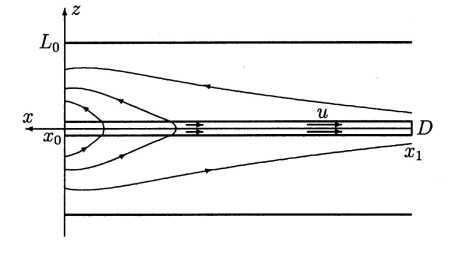
Рис . 1. Геометрические параметры модели .

Разумеется, модель не может правильно передать трехмерную структуру ближнего хвоста. Но начиная с расстояний 50–100 R E , где течение направлено от Земли и более однородно по ширине плазменного слоя, двумерная модель вполне приемлема.

Магнитное поле в долях хвоста полагается потенциальным

V- B = 0; Vx B = 0,

а в плазменном слое магнитное поле удовлетворяет уравнению

a ( E + u x B ) = — Vx B , µ₀

направлено от Земли при скорости в несколько сотен километров в секунду. На меньших расстояниях наблюдаются течения как в антисолнечном направлении, так и течения, направленные к Земле. При этом в ближней области (< 50 R _E) величины скорости лежат вблизи или ниже порога регистрации. Зависимость усредненной по ширине плазменного слоя скорости течения от координаты x из [Slavin, et al., 1985] показана на рис. 2 ломаной линией.

По данным «Geotail» [Hori, et al., 2000], в ближнем плазменном слое преобладают течения, направленные к Земле. Однако в стационарных условиях течение не может быть направлено строго к Земле по всей ширине плазменного слоя. В противном случае вынос магнитных силовых трубок из магнитосферного хвоста привел бы к его исчезновению. По-видимому, усредненная картина течения в ближнем плазменном слое включает как течение, направленное к Земле в центральных областях ближнего плазменного слоя, так и течение в антисолнечном направлении на флангах плазменного слоя, примыкающих к магнитопаузе .

К сожалению, зависимость скорости от координаты y нельзя учесть в рамках простой двумерной модели, для этого требуется более сложная трехмерная модель. В двумерной же модели фактически задается скорость течения u = u ( x ), средняя по ширине плазменного слоя. По этой причине нами использована упрощенная зависимость, в которой скорость, направленная от Земли, изменяется линейно от нуля в начале плазменного слоя при x = x 0 до максимального значения u 0 = 400 км/с при x 1 = 200 R E :

. .         x - xn u (x) = - u 0------.                                   (1)

x ₁

Соотношению (1) соответствует прямая линия на рис. 2.

где σ – проводимость плазмы. Вектор электрического поля E в двумерной модели имеет только постоянную y -компоненту E .

Переходя к у -компоненте векторного потенциала магнитного поля A ( x , z )

_R _ ^d A._R _AA B x =^-a ?' ^B = a x

и безразмерным переменным, получаем уравнения для долей хвоста

d ² A d ² A _л а? ⁺ az=⁰

и плазменного слоя

d A        1 ( d ² A d ² A )

u — - E =---1 ~ + ^гт I,

d x      Re m ^ d x   d z ² J

где Rе_m = µ₀σu₀ D – магнитное число Рейнольдса;

размерные переменные отнесены к характерному масштабу L ₀ = 25 R _E, скорости u ₀ = 400 км/с, B ₀ = 1 нТл.

Магнитное число Рейнольдса определено в данном случае по толщине плазменного слоя D , так как при условии D << L 0 определяющим масштабом задачи являются именно толщина плазменного слоя. Задача решается для верхней полуплоскости z >0. На границах прямоугольной области ставятся следую-

щие граничные условия:

Z = Lo: |A = 0; z = 0: |A = 0; dx             az x = x0: A(x0,z) = A0(z); x = x1:

fA = 0. d x

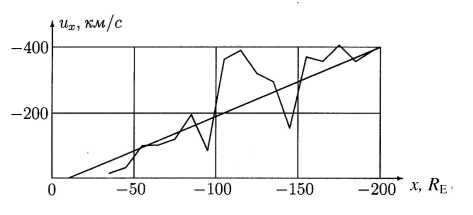
Рис . 2. Распределение скорости в плазменном слое .

Первое условие определяет равенство нулю нормальной компоненты магнитного поля на магнитопаузе, второе условие – симметрия. Третье условие задает распределение B x в начальном сечении магнитосферного хвоста. Нами использовано магнитное поле модели [Китаев, 1996b] при x 0 = -7 R E и y = 0. Последнее условие – приближенное и обычно задается в задачах с полубесконечной областью решения. При x 1 = -250 R E неточность данного условия практически не влияет на решение на расстояниях x > -200 R E . Кроме того , на границе плазменного слоя задается условие непрерывности компонент магнитного поля:

D

dA dx d /2+0

dA dx d /2—0

d A

D /2 + 0

d A

D /2 - 0

Решение задачи (4)–(7) получено при помощи численных методов.

Результаты расчетов и заключение

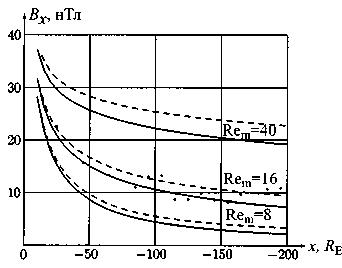
На рис. 3 приведены графики зависимости компоненты магнитного B_x в долях магнитосферного хвоста от координаты x , рассчитанные для значений магнитного числа Рейнольдса Rе_m=8, 16 и 40. Сплошными линиями на графиках показано решение при нулевом электрическом поле E =0, штриховые линии соответствуют электрическому полю утро–вечер, которое получается при разности электрических потенциалов поперек магнитосферного хвоста ΔФ=20 кВ. Точками на рисунке показаны усредненные данные измерений величины магнитного поля в долях хвоста из [Slavin, et al., 1985].

Как видно из графиков, электрическое поле утро–вечер при разности потенциалов 20 кВ приводит к некоторому увеличению тока в плазменном слое и увеличению магнитного поля в долях хвоста. Влияние проводимости на магнитное поле магнитосферного хвоста более заметно.

Хорошее согласие c усредненными данным [Slavin, et al., 1985] по распределению магнитного поля в хвосте получается при Rе_m=16. Это значение магнитного числа Рейнольдса можно сравнить с оценками, выполненными в [Cattell, 1996] на основе измерений уровня флуктуаций электрического поля в плазменном слое. В [Cattell, 1996] приведены оценки числа Лундквиста, которое отличается от числа Рейнольдса тем, что вместо характерной скорости течения u 0 в безразмерный параметр входит характерная альф-веновская скорость. Если пересчитать Rе m , взяв вместо u 0 альфвеновскую скорость, определенную по магнитному полю в долях хвоста и по плотности плазмы в плазменном слое на расстоянии 100 R E из [Slavin, et al., 1985], получим значение порядка единицы.

По оценкам [Raeder, et al., 1996], значение числа Лундквиста для дальнего плазменного слоя (100 R _E) лежит в пределах от 0.1 до 30, при этом большие значения соответствуют большей толщине плазменного слоя. Полученное выше значение Rе_m лежит в указанных пределах. Однако следует заметить, что количественное совпадение в данном случае можно рассматривать только как совпадение по порядку величины, так как оценки [Cattell, 1996] весьма приближенны, а полученное нами значение Rе_m соответствует некоторому усредненному состоянию магнитосферного хвоста. Кроме того, в рамках упрощенной модели не учтены многие факторы, действующие в ближнем плазменном слое . Например, если рассмотреть задачу, в которой течение в центральной части ближнего плазменного слоя направлено в сторону Земли, то будет получено несколько иное распределение компонент магнитного поля в хвосте, и значение Rе_m также изменится.

Из сравнения графиков B x видно, что при увеличении или уменьшении Rе_m вдвое (отклонение в ту или другую сторону от среднего значения), величина магнитного поля в дальнем хвосте выходит за пределы реально наблюдаемых значений. Это означает, что стационарные конфигурации магнитосферного хвоста возможны только в узком диапазоне значений проводимостей в плазменном слое. В то же время представляется маловероятным, что при сильной изменчивости условий в солнечном ветре и магнитосфере проводимость в плазменном слое колеблется лишь в небольших пределах. Естественно предположить, что в данном случае должен действовать механизм подстройки эффективной проводимости в плазменном слое к условиям в магнитосферном хвосте. Например, увеличение проводимости будет приводить к росту магнитного поля в долях хвоста и, следовательно, к увеличению тока в плазменном слое. Это, в свою очередь, может привести к росту аномального сопротивления [Липеровский, Пудовкин, 1983]. Возможно также, что в некоторых случаях стационарное состояние в магнитосферном хвосте невозможно, о чем свидетельствуют многочисленные наблюдения и результаты глобального МГД-моделирования, например [Raeder, et al., 1995].

Работа выполнена при финансовой поддержке РФФИ, грант 07-05-00135.