Перепутывание атомов, индуцированное тепловым шумом при наличии начальной атомной когерентности

Описание динамики кубитов, взаимодействующих с электромагнитными полями, является одной из наиболее актуальных проблем современной физики квантовых вычислений [1]. Такие системы активно изучаются как с теоретической, так и с экспериментальной точек зрения в одноатомных мазерах и лазерах, ионах в резонаторах и магнитных ловушках, сверхпроводящих системах на джозефсоновских переходах, квантовых точках [2]. Исследования таких физических систем позволили создать прообразы квантовых компьютеров, работающих пока на десятках кубитов. Дальнейший прогресс в данной области требует исследования как новых физических устройств, которые можно использовать в качестве логических элементов квантовых компьютеров, так и наиболее оптимальных режимов работы таких систем, в том числе наиболее эффективных схем генерации и контроля перепутывания состояний кубитов, а также особенностей их релаксации. Для приложений в физике квантовых вычислений нужны максимально перепутанные чистые состояния с достаточно большим временем жизни, однако в реальных условиях квантовые системы всегда взаимодействуют с окружением. Такое взаимодействие обычно приводит к декогерентности, так что исследуемая система эволюционирует в сме шанное неперепутанное (сепарабельное) состояние, которое оказывается непригодным для целей квантовых вычислений. Поэтому с практической точки зрения основная задача при получении и использовании атомных перепутанных состояний заключается в том, чтобы минимизировать влияние шума. Недавно была высказана идея о том, что в некоторых случаях диссипация и шум могут, напротив, являться источником перепутывания [3]. В частности, была показана возможность генерации перепутывания атомных систем в резонаторах, индуцированных тепловым шумом [4–8].

В работе [4] было показано, что одномодовый тепловой шум может индуцировать атом-атом-ное перепутывание в системе двух двухуровневых атомов в идеальном резонаторе. Позднее аналогичное поведение было обнаружено и для атомов с многофотонными переходами [5]. При этом было показано, что при двухфотонном взаимодействии атомов с тепловым полем степень перепутывания атомных состояний может значительно превосходить соответствующую величину для однофотонного взаимодействия. Позднее в целом ряде работ исследовались особенности генерации атомного перепутывания в различных обобщениях двухатомной модели Тависа – Каммингса для резонаторного поля в тепловом состоянии. Недавно на примере системы двух атомов, резонансно взаимодействующих с одномодовым тепловым полем [6], было показано, что степень перепутывания атомов сильно зависит от их начального состояния. Обнаружено, что при наличии атомной когерентности степень атомного перепутывания может заметно возрастать и что степенью атомного перепутывания можно управлять, изменяя относительные фазы и амплитуды поляризованных атомов. Было также показано, что наличие диполь-дипольного взаимодействия кубитов может существенно увеличить степень их перепутывания [7; 8].

В настоящей статье автор исследует влияние начальной атомной когерентности и диполь-ди-польного взаимодействия и атомной когерентности на перепутывание в случае нерезонансного взаимодействия кубитов с полем одномодового резонатора в тепловом состоянии.

1.    Модель и ее точное решение

Рассмотрим два идентичных кубита (ридберговские атомы, сверхппроводящие кубиты с джозеф-соновскими переходами, примесные атомные или ядерные спины, квантовые точки и т. д.) с частотой перехода Юо , нерезонансно взаимодействующих с выделенной модой электромагнитного поля идеального резонатора с частотой ю. Учтем также прямое диполь-дипольное взаимодействие между кубитами. Тогда в системе отсчета, вращающейся с частотой моды поля ю, гамильтониан такой си- стемы можно представить в виде

H = й 5с ^ + й 5а 2 +

+ й g ^ (а + a + a+а -) + йJ (^+^2 + о-о+ ), i=1,2

где а Z - оператор инверсии для i ( i = 1,2); а + =1 +) ii (— I и а - = | -) _и (+ | - операторы перехода между возбужденным | +) i и невозбужденным | -) i состояниями i -го кубита ( i = 1,2); a ⁺ и a -операторы рождения и уничтожения фотонов резонаторной моды; g – константа кубит-фотонного взаимодействия; 5 - параметр расстройки, равный S = Ю о -ю, и J - параметр прямого диполь-дипольного взаимодействия кубитов.

В качестве начальных состояний атомов выбе- рем когерентные состояния вида

| ^(0) ) = cos 0 1 | +) + e ^1 sin 0 1 | -) ,

| ^2(0)) = cos02 | +) + e^2 sin02 | -), где Ф1 и Ф2 - относительные фазы возбужденно го и невозбужденного состояний кубитов, а θ1 и

02 - параметры, определяющие начальную поляризацию кубитов. В качестве начального состояния поля резонатора выберем одномодовое тепло вое состояние

Р F (0) = ^ Р n । n X n ।.

Здесь ⁿ

=nn pn   (1+n)n+1, где n - среднее число тепловых фотонов в резонаторной моде, определяемое формулой Бозе – Эйнштейна n =(exp[йюi / kBT] -1) 1, kB ‒ постоянная Больцмана; T ‒ температура резонатора.

Найдем точную динамику представленной модели. Начнем исследование для случая, когда резонаторное поле приготовлено в состоянии с определенным числом фотонов, а затем обобщим полученные результаты на случай теплового поля резонатора. Для фоковского состояния поля и чистых начальных состояний атомов состояние всей системы определяется во все последующие моменты времени волновой функций. Решение временного уравнения Шредингера для рассматриваемых начальных состояний можно представить в виде разложения по собственным функциям гамильтониана (1) (представление «одетых состояний»). Пусть число элементарных возбуждений в системе с гамильтонианом (1) есть n (n > 0). Тогда собственные функции гамильтониана (1) в базисе | -, -, n + 2), | +,-, n +1), | -, +, n +1), | +, +, n) могут быть представлены в виде

| Ψ _in 〉 = w_in ( X_{i 1 n} | - , - , n + 2 〉+ X_{i 2 n} | + , - , n + 1 〉+       ₍₂₎

+Xi3n|-,+,n+1〉+Xi4n|+,+,n〉), где

W in =1/ V| X i 1 n |² + | X i 2 n |² +l X i 3 n |² + | X i 4 n |² ,

X _{11 n} =0, X _{12 n} = - 1, X _{13 n} =1, X _{14 n} =0,

_{X =} -      21 + n 2 + n

• 4    + 2 n + 2 5 + s in ^- 2 5s in ^- s in

1 + n (2 δ+ε _in )

^xi 2 n =   , „                         ₂

4 + 2 n + 2 δ+ε _in 2 δε _in ε _in

1 + n (2 δ+ε _in )

^Xi 3 n =   . „                         ₂

4 + 2 n + 2 δ+ε _in 2 δε _in ε _in

( i = 2,3,4),

X i 4 n =1

• ⁵    = ^A / Y ,   ^s in = E in / ^й g .

Соответствующие собственные значения энергии можно представить как

E in = Й g a , E 2 n = (1 / 3) h gRe [( a + A n / B n + B n )],

E 3 n =(1/6)^ g x x Re[2a — (1 + iV3)A. / B. + i(i + V3)B. )], nn     n

E 4 n =(1/ 6)й g x x Re[2a + i(i + 73)A / Bn — (1 + i73)Bn)], nn     n где

A n =18 + 12 n + a ² + 12 5 2 ,

B n = ( a ³ — 54 5 + 9 a ( 3 + 2 n — 4 5 ² ) + + ¹ I — 4 ( 18 + 12 n + a ² + 12 5 ² ) 3 +

+ 4 ( a ³ — 54 5 + 9 a ( 3 + 2 n — 4 5 ² a = J / y .

■ ■ :T

,

Для получения полной динамики нашей модели мы должны также ввести в рассмотрение собственные функции гамильтониана (1) вида | — , — ,1 ) , I ⁺ , ^{— ,0 ) ,} | ^— , ^{+ ,0 )} , | ^— , ^{— ,0} >

Предположим, что начальное состояние исследуемой системы есть | +, —, n +1) (n > 0). Тогда в момент времени t состояние системы можно описать вектором состояния

| ^ ⁽ t ) > = Сц,n | ^— , ^— , ^{n + 2 ) +} C 22, n | ⁺ , ^— , ^{n +} 1 >⁺

⁺ C 32, n ^{1 —} , ⁺ , ^{n +} 1 >⁺ C 42, n ^{1 +} , ⁺ , ⁿ > ,

C i 2, n ^-

• — iE t / Й                    — iE„ t / Й

1 n 2 n

1 n 2 in 1 in                 2 n 2 in 2 in

• — iE- t / Й                    — iE t / Й

3 n 4 n 3 n 2 in 3 in              4 n 2 in 4 in

• ⁽ i = ^1,2,3,4) , Y ijn = w X jin .

Если начальные состояния системы есть | + , — ,0 ) , то временная волновая функция имеет, соответственно, вид

| ^(t)> = C12 |—,—,1>+ C22 |+,—,0>+ C32 |—, +,0>,

C12 = —2ie—i(a—25)t/2 sin(Qt /2)/ Q, r _ o—i(a—25)t/2 /i(3a—25)t/2 ,

• C22 = e          (e+

+ Q cos(Q t /2) — 2 i sin(Q t / 2)) / (2Q), r       —i(a—25)t/2/ i(3a—25)t/2 ,

• C32 = e          ( e+

+ Q cos( Q t /2) — 2 i sin( Q t / 2)) / (2 Q ),

Q = Ts + ( a + 28)²".

Предположим, что наша система в начальный момент находится в состоянии | — , + , n + 1 ) . Тогда временная волновая функция может быть представлена в виде

| V ⁽ t ) > = C 13, n ^{1 —} , ^— , ^{n + 2} >⁺ C 23, n ^{1 +} , ^— , ^{n +} 1 >⁺

• ⁺ C 33, n ^{1 —} , + , ^{n +} 1 >⁺ C 43, n ¹ + , + , ⁿ > >

где коэффициентыe C_{i 3, n} имеют вид (8) при замене

Y 2 in на Y 3 in ( i =1, ² , ³ , 4).

Если начальное состояние системы есть | — , + ,0 > , то временная волновая функция примет вид | У ( t ) > = C 13 | — , — , 1 > + C 23 | + , — ,0 > + C 33 | — , + ,0 > ,       (6)

^где C 13 - C 12 , C 23 - C 22 , C 33 = C 32 ^.

Для начальных состояний | + , + , n > и | — , — , n + 2 > ( n >  0) временные волновые функции есть

| ^ ⁽ t ) > = C 11, _n | ^— , ^— , ⁿ + ² >⁺ C 21, _n | ⁺ , ^— , ^{n +} 1 >^{+ +} C 31, n | ^— , ⁺ , ^{n +} 1 >⁺ C 41, n | ⁺ , ⁺ , ⁿ > ;

| ^ ⁽ t ) > = C 14, n | ^— , ^— , ^{n + 2} >⁺ C 24, n | ⁺ , ^— , ^{n +} 1 >^{+ +} C 34, n | ^— , + , n ⁺ 1 >⁺ C 44, n | + , + , n > .

Коэффициенты C_{i 1, n} ( C_{i 4, n} ) могут быть получены из (3) путем замены Y 2in на Y 1 in ( Y 4in ) ( i = 1, 2, 3, 4).

Если начальное состояние системы | — , — ,1 > , временную волновую функцию можно представить как

| ^ ( t ) > = C 14 | — , — , 1 > + C 24 | + , — ,0 > + C 34 | — , + ,0 > ,       (9)

C ₁₄ ( t ) = e ^{— (1/2)} i ^{( a— 2 5 )} t ((8 + ( a + 2 5 )² cos( Q t / 2) +

+ ( a + 2 5 ) Q i sin( Q t /2))/( Q ²),

—it ( a— 2 5 )

C ₂₄( t ) = C ₃₄( t ) = — 2 ie ²        sin( Q t /2))/( Q ).

Наконец, для начального состояния | — , — ,0 > временная волновая функция есть

| ^ ( t ) > = exp[ — i (2 5 1 )] | — , — ,0 > .

Используя выражения (2)‒(9), мы можем найти явный вид матрицы плотности полной системы p Fock ( t )= | T ( t ) ><^ ( t )|. Используя выражение для матрицы плотности в случае фоковского начального состояния поля, легко получить явный вид матрицы плотности полной системы для теплового поля p Thermal ( t ). Выполняя усреднение полной матрицы плотности по переменным резонаторного поля, мы можем получить редуцированную матрицу плотности подсистемы кубитов p _А ( t ) = = Ti p p Thermal ( t ). Наконец, атомная матрица плотности может быть использована для вычисления параметра перепутывания кубитов.

2. Вычисление параметра перепутывания кубитов

р 13 =

В качестве параметра перепутывания кубитов мы воспользуемся параметром Переса - Хоро-

*

n =1

*

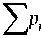
’ 42, n-1Z 34, n -2 + n=2

*V^                  *

= ^ab E P n Z 41, n^Z 32, n - 1 ⁺ ac

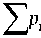
n =1

*

' 41, n^Z 33, n - 1 ⁺

децких или отрицательностью, которая может быть представлена в терминах отрицательных собственных значений ц - частично транспонированной по переменным одного кубита атомной матрицы плотности ( р A ):

s = - 2 ^ - . (10) i

Значения параметра (10), удовлетворяющие неравенству s >  0, соответствуют перепутанному состоянию кубитов, в то время как значение s = 0 соответствует сепарабельным состояниям кубитов. Для максимально перепутанных кубитов s = 1.

+cd * EPnZ n=2

*

*

' 43, n - 1 ^Z 34, n - 2 ⁺

*

*

*

^{+ p} 1^{( bd Z} 42,0 G 34 ⁺ cd ^Z 43,0 G 34 ) ⁺

*

*

^{+ p} 0^{( ab Z} 41,0 G 32

*~

^{+ ac Z} 41,0 G 33 ),

р 14 =

*             „*

- ad EpnZ41,nZ14,n-2 + n=2

+ P 1 ad Z ₄₁ ,1 G ₁₄ + p 0 ad Z ₄₁ , ₀, р 22 =

Для когерентных сепарабельных начальных состояний кубитов редуцированная атомная матрица плотности рассматриваемой модели в двуку-битном базисе | - , -) , | + , -) , | - , +) , | + , +) имеет вид

P11 р12 р13 р14 ^ P A(t ) = р21 р22 р23 р24 ,                           (11) P31 р32 р33 р34 чр41 р42 р43 р44 2 где р11 =

• =I a I2 Ep -'Zv- I2 +IdI2 EpnIZ24n. -212 + n=0

* V^ ~ V

• ⁺ bc E p n^Z 22, n - 1 ^Z 23, n - 1 ⁺

n =1

• * V'1 _

• ⁺    cb E p n^Z 23, n - 1 ^Z 22, n - 1 ⁺

n =1

• +    Ic 12 EPnIZ 23, n-1 12 +Ib 12 EPnIZ 22, n-1 12 + n=1

** '

• +    p1 | d | | G24 | + p0(| b | | G22 | + bc G22G23) + **

• +    P ₀ ( cb G ₂₃ G ₂₂ | c | | G ₂₃ | ),

• - a I² I p n\ Z 41, n I² + \b I² E P n IZ 42, n - 1 I² + n =0                     n =1

*

• ⁺    bc E p n^Z 42, n - 1 ^Z 43, n - 1 ⁺ n =1

• ⁺    cb EE ^Pn Z 43, n - 1 Z 42, n - 1 ⁺ n =1

• +    | c |² E p n | Z 43, n - l i² + |d |² E n^ 44, n - 2 |² • n =1                        n =2

р 23 =

n =0

*

n =1

*

^р 12 =

*V „   „*        *

= ^ab E P n Z 41, n^Z 22, n - 1 ⁺ ac n =1

*

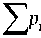
' 41, n^Z 23, n - 1 ⁺ n =1

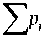
’ 42, n - 1 ^Z 24, n - 2 ⁺ n =2

⁺ cd E ^Pn Z 43, n - 1 Z 24, n - 2 ⁺ n =2

. *

*

. *

*

+ ^p 1⁽ bd Z 42,0 G 24 + cd Z 43,0 G 24 ) +

*

*

^{+ p} o^{( ab Z} 41,0 G 22

*„    ^*3

^{+ ac Z} 41,0 G 23 ),

'21, n^Z 31, n ^{+ I d 1 2}

*

’ 22, n - 1 ^Z 33, n - 1 ⁺

⁺ cb E p n^Z 23, n - 1 ^Z 32, n - 1 ⁺ n =1

^{+ I} c 2 E ^Pn^Z 23, n - 1 ^Z 33, n - 1 ⁺ n =1

*

E pnZ24,n-2Z34,n-2 + n=2

+ 1Ы² Yp          7 +

I I p n 22, n -1 32, n -1

n =1

*                            *

^{+ p [1]} | ^d | G 24 G 23 ^{+ p [0](| b} | G 22 G 32 ⁺

*^ /-.*       *z-. V 2      ^* X

+ bc G 22 G 33 ⁺ cb G 23 G 32 ⁺ | c | G 23 G 33 ),

р ₃₃ =

-I a I² E P n I Z 31, n

n =0

*

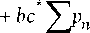
^Z 32, n - 1 ^Z 33, n - 1

n =1

1 ² + I b I² E P n I Z 32, n - 1 I² +

n =1

■\E          rZ

⁺ cb E ^Pn^Z 33, n - 1 ^Z 32, n - 1

+

n =1

а б

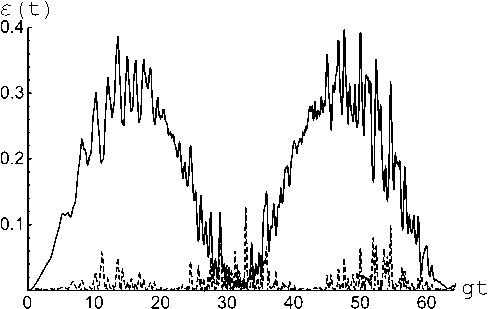
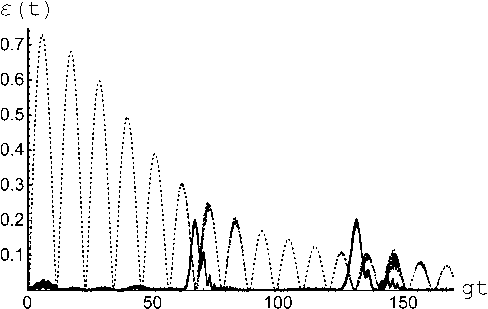
Рис. 1. Отрицательность как функция безразмерного времени gt для модели без диполь-дипольного взаимодействия в случае когерентного начального состояния кубитов с 6 1 =0 2 = п / 4, ф 1 = 0, ф 2 = п (сплошная линия) и сепарабельного состояния с 9 1 = 0, 6 ₂ = п , ф ₁ = 0, ф ₂ = 0 ( б) . Среднее число тепловых фотонов в моде n = 20, расстройка 6 = 0 ( а ) и 5 = 10 ( б )

Fig. 1. Negativity as a function of dimensionless time gt for a model without dipole-dipole interaction in the case of a coherent initial state of qubits with 6 1 =6 2 = п / 4, ф 1 = 0, ф ₂ =п (solid line) and a separable state with 6 1 = 0, 6 2 = п , ф ₁ = 0, ф ₂ = 0 ( b ). Average number of thermal photons in a mode n = 20, detuning 5 = 0 ( a ) and 5 = 10 ( b )

+ I c P T p n I Z 33,n - 1 I^{2 2} + I d P T p n I Z 34, n - 2 I² + n =1                         n =2

⁺ p 1 | d |²1 G 34 |² + ^p 0^{(| b} |²1 G 32 ^{| 2 +}

+ bc * G 32 G 33 + cb * G 33 G 3 ² 2 + I c P I G 33 P ),

	^ p 11 p 12 p 13   p 23
T p A ( t )=	*                 *        * p 12   p 22 p 14 p 24	.                            (12)
	p 13   p 14   p 33 p 34
	* tp 23 p 24   p 34   p 44 ;

^p 34 =

n =1

¹ n^Z 31, n^Z 12, n - 1 ^{+ ac} T p n^Z 31, n Z 13,n — 1 ⁺

n =1

* X--1

^{+ bd} T P n

n =2

Z 32, n - 1 ^Z 14, n - 2 ⁺

^{+ cd} T ^p n^Z33,n - 1 Z 14, n - 2 ⁺ n =2

+ p₁( bd * Z ₃₂ , ₀ G_u + cd * Z ₃₃ , ₀ G * ₄) +

+ P o( ab * Z 31,0 G 12 + ac * Z 310 G ^) +

+ p ₀( bd G 32 + cd G 33 ),

^p 44 =

=| a I² T p n I Z 11 I² + I b I² T P n I ^Z 12, n - 1 I² +

n =0

n =1

1 * v^

^{+ bc} T P n

n =1

^Z 12, n - 1 Z 13, n - 1

^{+ cb} T ^pn^Z 13, n - 1 ^Z 12, n - 1 ⁺

n =1

^{+ 1 c 1 2} T ^pn ¹ Z 13, n - 1 ^{1 2 + 1 d 1 2} T ^pn ¹ Z 14, n - 2 ^{1 2 +}

n =1

n =2

^{+ p} 1 I ^d I I ^G 14 I ^{+ p} 0⁽ l ^b I I ^G 12 I ^{+ bc G} 12 ^G 13 ⁺

*           *            .0.          .0      . - .0.

^{+ cb G} 13 G 12 ^{+ | c | | G} 13 ^{| + |} d ^| ).

Здесь a = cos 6 ₁ cos 6 2 , b = cos 6 ₁ sin 6 2 , c = sin 6 ₁ x x cos 6 2 , d = sin 6 ₁ sin 6 2 .

Соответственно, частично транспонированная по переменным одного кубита атомная матрица плотности p ^( t ) есть

Все четыре собственных значения матрицы могут принимать отрицательные значения, поэтому вносят вклад в отрицательность. Указанные собственные значения имеют чрезвычайно громозкий вид и поэтому не приводятся в настоящей статье.

3. Результаты численного моделирования отрицательности

Результаты численного моделирования временной зависимости параметра перепутывания кубитов приведены на рис. 1-2 для моделей с резонансным и нерезонансным кубит-полевым взаимодействием в случае интенсивного теплового поля резонатора.

На рис. 1, а представлена зависимость отрицательности от безрамерного времени gt для модели с резонансным взаимодействием между кубитами и полем в отсутствие диполь-диполь-дипольного взаимодействия кубитов. При этом cплошная кривая соответствует когерентному начальному состоянию кубитов вида | ^ 1 (0) ) = = (1 / V2)(| +) 1 + | -) 1 ), | Т 2 (0) ) = (1 / 72)(| +) 2 - | -) 2 ), а пунктирная - сепарабельному состоянию кубитов | Т 1 (0) ) = | +) ₁, | Т ₂ (0) ) = | -) ₂. Из рис. 1 хорошо видно, что в случае резонансного взаимодействия кубитов с полем резонатора наличие начальной атомной когерентности для определенных амплитуд поляризованных атомов приводит к суще-

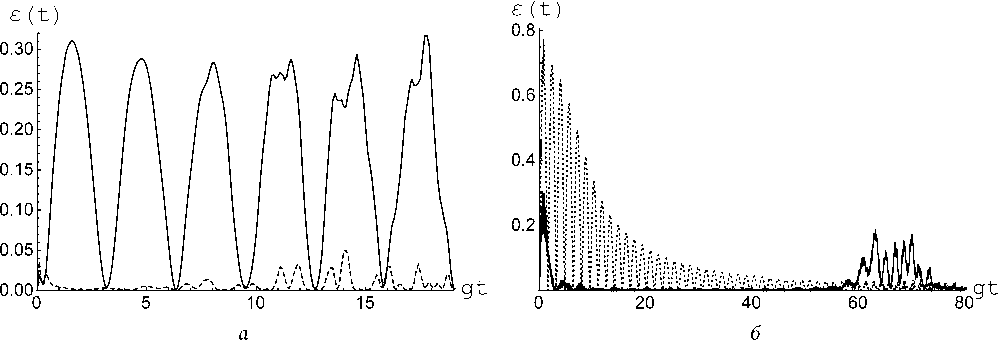
Рис. 2. Отрицательность как функция безрамерного времени gt для модели в присутствии диполь-дипольного взаимодействия в случае когерентного начального состояния кубитов с 9 1 =6 2 = п / 4, ф 1 = 0, ф 2 = п (сплошная линия) и сепарабельного состояния с 9 1 = 0, 9 2 = п , ф 1 = 0, ф ₂ = 0 ( 6 ). Среднее число тепловых фотонов в моде n = 20, параметр диполь-дипольного взаимодействия кубитов а = 1, расстройка 5 = 0 ( а ) и 5 = 10 ( 6)

Fig. 2. Negativity as a function of dimensionless time gt for the model in the presence of dipole-dipole interaction in the case of a coherent initial state of qubits with 9 1 =9 2 = п / 4, ф 1 = 0, ф ₂ = п (solid line) and a separable state with 9 1 = 0, 9 2 = п , ф 1 = 0, ф ₂ = 0 ( b ). Average number of thermal photons in a mode n = 20, parameter of dipole-dipole interaction of qubits a = 1, detuning 5 = 0 ( a ) and δ= 10 ( b )

ственному возрастанию максимальной степени перепутывания. На рис. 1, 6 представлена зависимость отрицательности от безрамерного времени gt для модели с нерезонансным взаимодействием между кубитами и полем в отсутствие диполь-дипольного взаимодействия кубитов. При этом, как и для рис. 1, a , сплошная кривая соответствует когерентному начальному состоянию кубитов | Т 1 (0) ) = (1 /V2) X (| +) 1 + | -) 1 ), | Т 2 (0) ) = = (1 / V2 )(| +) ₂ - 1 -) 2 ), а пунктирная - сепарабельному состоянию | Т 1 (0) ) = | +) 1 , | Т ₂ (0) ) = | -) ₂. В случае нерезонансного атом-полевого взаимодействия характер зависимости степени перепутывания кубитов от начальной когерентности меняется на противоположный. Для нерезонансного взаимодействия максимальная степень перепутывания кубитов для сепарабельного состояния превышает соответствующую величину для когерентного состояния. Можно отметить еще одну интересную особенность в поведении отрицательности в случае нерезонансного кубит-полевого взаимодействия. В этом случае осцилляции отрицательности затухают и на больших временах обращаются в ноль (т. е. за счет расстройки нелокальные квантовые корреляции кубитов исчезают, несмотря на отсутствие диссипации в рассматриваемой модели). В то же время поведение, как и для резонансной модели поведение отрицательности, носит квазипериодический характер.

На рис. 2 представлены временные зависимости отрицательности в случае резонансной ( a ) и нерезонансной ( б ) моделей в присутствии прямого диполь-дипольного взаимодействия кубитов. Результаты для рассматриваемого случая качественно аналогичны результатам для модели без ди-поль-дипольного взаимодействия. Заметим, что в отсутствие диполь-дипольной связи и большого среднего числа фотонов степень перепутывания кубитов очень мала.

Заключение

Таким образом, в настоящей статье автор исследовал влияние атомной когерентности на перепутывание двух дипольно связанных двухуровневых естественных или искусственных атомов (кубитов), взаимодействующих с интенсивным тепловым одномодовым полем резонатора без потерь. Результаты расчетов показывают, что максимальная степень перепутывания кубитов может существенно возрастать при наличии начальной атомной когерентности в случае резонансного взаимодействия кубитов с тепловым полем. При ненулевой расстройке начальная атомная когерентность, напротив, уменьшает степень перепутывания кубитов. Полученные результаты могут быть использованы при разработке механизмов управления и контроля степени перепутывания кубитов в квантовых компьютерах и квантовых сетях.