Перепутывание атомов, последовательно пролетающих резонатор с тепловым полем

Атомные перепутанные состояния являются основным ресурсом физики квантовых вычислений и квантовой информатики. В настоящее время предложены и экспериментально реализованы различные схемы генерации перепутывания состояний атомов и ионов в резонаторах и оптических и магнитных ловушках, а также различных искусственных атомных объектов, таких как квантовые точки, примеси в твердых телах, сверхпроводящие цепи с джозефсонов-скими переходами и др. [1]. Одним из очевидных кандидатов на роль кубита, который является управляемой системой на двух уровнях, становится нейтральный атом [2]. Кубиты, закодированные на уровнях атомной энергии, могут быть легко приготовлены в требуемом состоянии при использовании оптической накачки и лазерного охлаждения и могут достаточно легко управляться с помощью электромагнитного излучения. Нейтральные атомы хорошо подходят на роль кубитов также из-за их слабого взаимодействия с окружающей средой, что приводит к длинным временам когерентности. Перспектива генерации многокубитных перепутанных состояний вместе с возможностью локальной адресации и измерения делает нейтральные атомы весьма обещающими объектами для физики квантовых вычислений. Одним из способов исследования особенностей перепутывания нейтральных рид- берговских атомов является одноатомный мазер. В экспериментах с одноатомным мазером для двух атомов, последовательно пролетающих резонатор с вакуумным состоянием поля, наблюдались как белловские двухчастичные атомные перепутанные состояния [3], так и трехчастичные атом-полевые перепутанные состояния Гринберга – Хорна – Цайлингера [4]. В эксперименте [3] по генерации ЭПР атомного перепутанного состояния два изначально независимых двухуровневых ридберговских атома последовательно пролетали высокодобротный резонатор с вакуумным полем. При этом первый из пары атомов приготавливался в возбужденном, а второй – в основном состоянии. Скорость первого атома подбиралась так, чтобы время взаимодействия этого атома с вакуумном полем τ удовлетворяло условию Ωτ = π /2, где Ω – вакуумная частота Раби, которая определяет скорость обмена фотоном атома и резонатора. Скорость второго атома выбиралась в два раза меньшей, чем у первого атома. Тогда время взаимодействия второго атома с вакуумным полем удовлетворяло условию Ωt = π. В результате такого взаимодействия состояния атомов максимально запутывались. Анализ распределения конечных состояний атомов позволил авторам сделать вывод о наличии перепутывания их состояний, степень которого составляла примерно 63 % от предсказываемого максимально возможного значения.

В ряде работ [5–8] была теоретически предсказана возможность генерации перепутывания атомов с одно- и двухфотонными переходами, последовательно пролетающих через резонатор, в котором поле приготовлено в различных квантовых состояниях, в том числе и в тепловом состоянии. В ряде недавних работ, посвященных исследованию перепутывания в системе двух атомов, одновременно взаимодействующих с тепловой модой резонатора [9–13], было также показано. что начальная атомная когерентность может существенно увеличить степень атомного перепутывания. Представляет интерес изучить влияние начальной атомной когерентности на перепутывание атомов, последовательно пролетающих резонатор. Такая задача рассматривалась ранее в работе [14], однако ее авторы не учли все возможные квантовые корреляции, возникающие между атомами.

Таким образом, в настоящей работе нами исследована зависимость поведения перепутывания двух атомов, последовательно пролетающих тепловой резонатор, от степени их начальной когерентности и интенсивности теплового поля резонатора.

1.    Описание модели

Рассмотрим систему двух идентичных двухуровневых атомов, приготовленных в перепутанном состоянии. Предположим, что атомы движутся в направлении некоторой выделенной оси, перпендикулярной оси резонатора, со скоростями v ₁ и v ₂ соответственно и последовательно один за другим пролетают через основной микрорезонатор, в котором резонансно взаимодействуют с электромагнитным полем посредством вырожденных однофотонных переходов. То есть мы предполагаем, что в момент времени, когда первый атом покидает резонатор, второй в него влетает. Времена пролета атомами резонатора составят τ и t соответственно. Гамильтониан резонансного взаимодействия атома с полем резонатора в дипольном приближении и приближении вращающейся волны есть

H = Й g ( а + о - + g⁺ a ), (1) где a ⁺ ( a ) – оператор рождения (уничтожения) фотонов резонаторной моды поля; σ⁺ и σ^- – повышающий и понижающий оператор в двухуровневом атоме; g – эффективная константа взаимодействия атома с полем.

Мы будем полагать, что перед пролетом через микрорезонатор каждый из атомов с помо- щью диодного лазера в предварительном боксе переводится в когерентную смесь возбужденного и основного состояний вида

| Ψ ₁(0) 〉 = cos θ ₁| +〉 + e^{i ϕ 1} sin θ ₁| -〉 ,

| Ψ 2 (0) 〉 =cos θ 2 | +〉+ e^{i ϕ 2}sin θ 2 | -〉 .             (2)

Здесь θ ₁ и θ ₂ – амплитуды поляризованных атомов и ϕ ₁ и ϕ ₂ – относительные фазы атомов соответственно.

В качестве начального состояния поля мы будем рассматривать одномодовое тепловое поле, состояние которого определяется матрицей плотности вида

ρ _F (0)= ∑ p _n | n 〉〈 n |,                           (3)

n где весовые множители есть nn pn (1 + n)n+1 .

Здесь n – среднее число фотонов в резонаторе n = (ехр[Йюi / квТ] - 1]-1, где kB – постоянная Больцмана и T – равновесная температура резонатора.

2.    Вычисление параметра перепутывания двух атомов

Для определения степени атом-атомного перепутывания будем использовать параметр Переса – Хородецких, определим ее стандартным образом [15]

ε = - 2 ∑ µ i ^- ,                                   (4)

i где µi- – отрицательные собственные значения частично транспонированной по переменным одного кубита (атома) редуцированной матрицы плотности. Для неперепутанных состояний ε = 0. Для перепутанных состояний 0 < ε≤1. Максимальной степени перепутывания соответствует значение ε = 1.

Решая квантовое уравнение Лиувилля для двух последовательных этапов взаимодействия каждого из атомов с полем резонатора, описываемым гамильтонианом 91), с учетом начальных условий (2) и (3) мы можем найти явный вид временной матрицы плотности полной системы в момент вылета второго атома из резонатора. Усредняя ее по переменным поля, можно получить редуцированную атомную матрицу плотности в двухатомном базисе | + , +〉 , | + , -〉 , | - , +〉 , | - , -〉 вида

p11 p12  p13 p14 ^ P*2 P22 P23 P24 Pat(T, t) = . *        * . p13 p23 p33 p34 *        *        * (p14  p24 p34 p44 у Здесь P11 = /P n(| X1 n |2 + | X2n |2 + | X3n |2), n /XT XT *    . XT   XT* X p12 = /p n(X1 n X 4 n + X 2 n X 5 n ), n p13 = / Pn(X1 nX7n + X2nX9n), n

X 12 _n ( t , t ) = - a sin( V n + 1 g T )sin( V n + 2 gt ).

(5)	Частично транспонированная по переменным одного кубита редуцированная атомная матрица
	плотности	для	(5) может быть представлена в
	виде	pn	„*    „* p 12 p 13 p 23
	p at ( T , t )=	* p 12 p 13 4 p 23	*        * p 22   p 14   p 24                     (6) p 14   p 33   p 34 P 24   P 34   P 44J

P 14 =

* X 1 n X 10 n ,

n

^p 22 = / p n (I X 4 n | 2 + I X 5 n | 2 + I X 6 n ^{| 2 )} , n

Собственные значения частично транспонированной по переменным одного кубита матрицы плотности (6) можно найти только численным способом. В следующем разделе представлено временное поведение параметра перепутывания (4) для различных параметров модели и одинаковых скростей движения атомов, т. е. при ус-

p23 = / Pn(X4nX7n + X5nX9n + X6nX8n), ловииt = t.

n

*

*

^p 24 = / P n ⁽ X 4 n X 10 n + X 6 n X 11 n ),

n

• ^p 33 = / p n ^(| X 7 n | 2 + | X 8 n | 2 + | X 9 n ^{| 2 )} ,

n

P 34 = / P n ( X 7 n X 1*0 n + X 8 n X *1 n ),

n p44 = /pn(| X10n |2 + | X11 n 2 + | X12n |2), n где

X 1 _n ( t , t ) = a cos(V n + 1 g t ) cos(V n + 1 gt ),

X 2 _n ( t , t ) = - i ( c sin( V ng t ) cos( 4ngt ) +

+ b cos(V n + 1 g t ) sin( 4ngt ) ) ,

X 3 n ( t , t ) = - d sin( V ng t ) sin(V( n - 1) gt ),

X 4 _n ( t , t ) = - c sin( V ng T )sin( 4ngt ) +

+ b cos( V n + 1 g t ) cos( 4ngt ),

X 5 _n ( t , t ) = - id sin( V ng T )cos(V( n - 1) gt ),

X 6 _n ( t , t ) = - ia cos(V n + 1 g T )sin(V n + 1 gt ), X 7 _n ( t , t ) = c cos( V ng t ) cos(V n + 1 gt ) -- b sin(V n + 1 g T )sin(V n + 1 gt ),

X 8 _n ( t , t ) = - ia sin(V n + 1 g T )cos(V n + 2 gt ),

X 9 _n ( t , t ) = - id cos( V ng T )sin( Jngt ),

X 10 _n ( t , t ) = d cos(V ng t ) cos( 4ngt ),

X 11 _n ( t , t ) = - i ( c cos(V ng t ) sin(V n + 1 gt ) + + b sin( V n + 1 g t ) cos( V n + 1 gt ) ) ,

3.    Обсуждение результатов

Результаты численного моделирования параметра перепутывания (4) для различных начальных состояний атомов и интенсивностей теплового поля резонатора представлены на рис. 1–3. На рис. 1 и 2 показана зависимость параметра Переса – Хородецких от степенени атомной когерентности, а на рис. 3 – от среднего числа фотонов в резонаторной моде. Из рисунков хорошо видно, что перепутывание атомов за счет взаимодействия с тепловым полем резонатора возникает для любых начальных атомных состояний, в частности, для случая, когда оба атома первоначально возбуждены. При этом начальная атомная когерентность приводит к уменьшению степени перепутывания. Такое поведение пере-

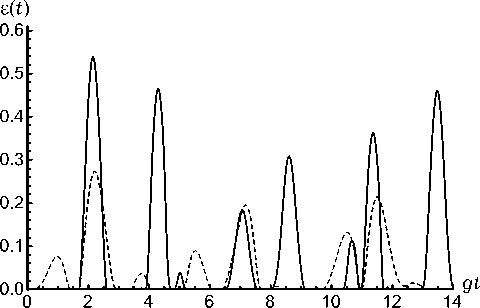
Рис. 1. Зависимость параметра перепутывания от безразмерного времени gt . Среднее число тепловых фотонов в резонаторной моде n = 0.1. Амплитуды поляризованных атомов 0 1 = 0 2 = 0, (сплошная линия) и 0 1 = 0 2 = п /4 (точечная линия)

£(t)

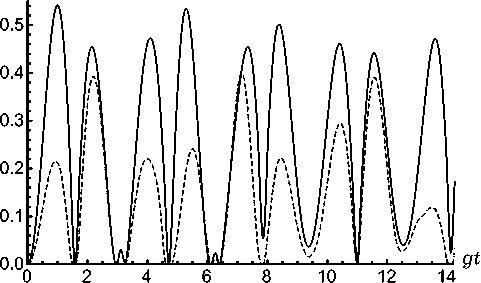
Рис. 2. Зависимость параметра перепутывания от безразмерного времени gt . Среднее число тепловых фотонов в резонаторной моде n = 0.1. Амплитуды поляризованных атомов θ ₁ = 0, θ ₂ = π /2, (сплошная линия) и θ ₁ = π / 6, θ ₂ = π /3 (точечная линия)

путывания для атомов, последовательно пролетающих резонатор, принципиально отличается от его поведения для атомов, одновременно взаимодействующих с тепловым полем в резонаторе. В последнем случае наличие начальной атомной когерентности приводит к существенному увеличению атомного перепутывания даже в случае интенсивного теплового поля [9; 10]. Кроме того, для атомов, одновременно запертых в резонаторе и приготовленных в возбужденных состояних, электромагнитное поле не приводит к перепутыванию их состояний ни для каких значений константы атом-полевого взаимодействия [11–13]. Рис. 3 показывает, что квантовые корреляции между атомами, последовательно пролетающими микрорезонатор, возникают только для тепловых полей малой интенсивности, когда среднее число фотонов в моде не превосходит единицы или, соответственно, температура резонатора не превосходит 4 K.

Заключение

Таким образом, нами исследована динамика перепутывания состояний двух двухуровневых атомов, последовательно пролетающих микрорезонатор одноатомного мазера с тепловым одномодовым полем, в случае, когда атомы перед пролетом микрорезонатора с помощью диодного лазера в предварительном боксе переводятся в когерентную суперпозицию возбужденного и основного состояний. В работе показано, что взаимодействие атомов с тепловым полем достаточно малой интенсивности приводит к перепутыванию их состояний для любых их начальных состояний, в том числе для начального состояния, в котором оба атома возбуждены. Пока-

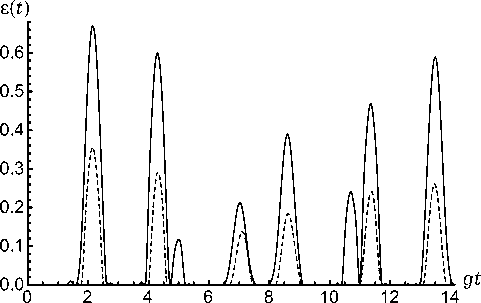
Рис. 3. Зависимость параметра перепутывания от безразмерного времени gt . Амплитуды поляризованных атомов θ ₁= θ ₂= 0. Среднее число тепловых фотонов в резонаторной моде n = 0 (сплошная линия) и n = 0.5 (штриховая линия)

зано также, что наведение начальной атомной когерентности приводит к уменьшению степени перепутывания атомов. В настоящей работе мы считали резонатор идеальным. Рассмотрение более реалистичной модели перепутывания атомов, последовательно пролетающих резонатор с конечной добротностью, учитывающей энергетическую и фазовую диссипацию будет являться предметом нашей следующей работы.

Работа выполнена в рамках госзадания Министерства образования и науки Российской Федерации № 1394.