Перепутывание двух сверхпроводящих кубитов, индуцированное тепловым шумом резонатора со средой Керра, при наличии начальной атомной когерентности
Автор: Башкиров Е.К.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 1 т.25, 2022 года.
Бесплатный доступ
Рассмотрена система, состоящая из двух идентичных искусственных атомов (кубитов), резонансно взаимодействующих с модой квантового поля идеального микроволнового резонатора при наличии керровской нелинейности. Для рассматриваемой модели получено точное решение квантового уравнения Лиувилля для полной матрицы плотности системы «два кубита + мода поля резонатора». Для решения квантового уравнения эволюции использовано представление «одетых» состояний, то есть собственных функций гамильтониана. Найден полный набор «одетых» состояний рассматриваемой модели. С его помощью первоначально найдено решение уравнения эволюции для когерентных начальных состояний кубитов и фоковских состояний поля, то есть состояний с определенным числом фотонов в резонаторной моде. Затем проведено обобщение указанного решения на случай теплового состояния поля резонатора. Усредняя полную матрицу плотности по переменным поля резонатора, мы нашли редуцированную матрицу плотности двух кубитов. Двухкубитная матрица плотности использована для вычисления параметра перепутывания кубитов в аналитическом виде. В качестве количественного критерия перепутывания кубитов выбрана согласованность. Ввиду особой громоздкости полученного выражения для согласованности проведено численное моделирование временной зависимости согласованности кубитов для различных параметров модели и начальных состояний кубитов. Наиболее интересным представляется результат, заключающийся в том, что учет начальной когерентности кубитов в модели с керровской нелинейностью приводит к существенному увеличению максимальной степени перепутывания кубитов, индуцированного тепловым полем, даже в случае больших интенсивностей поля резонатора.
Сверхпроводящие кубиты, микроволновй копланарный резонатор, тепловой шум, керровская нелинейность, перепутывание, отрицательность, начальная когерентность кубитов
Короткий адрес: https://sciup.org/140290783
IDR: 140290783 | УДК: 535.1 | DOI: 10.18469/1810-3189.2022.25.1.7-15
Текст научной статьи Перепутывание двух сверхпроводящих кубитов, индуцированное тепловым шумом резонатора со средой Керра, при наличии начальной атомной когерентности
Исследование взаимодействия между квантовыми подсистемами имеет фундаментальное значение в области квантовой обработки информации, поскольку оно является источником перепутывания состояний таких подсистем. Система, состоящая из двух взаимодействующих кубитов, является одной из самых простых квантовых систем, демонстрирующих совместные неклассические особенности, такие как перепутывание. Воздействие на отдельные кубиты, а также связывание удаленных кубитов в единую квантовую систему обычно осуществляется с помощью электромагнитных полей резонаторов. Такой тип связи требует детального изучения особенностей взаимодействия кубитов и фотонов резонаторов. Такой тип взаимодействия активно изучается как теоретически, так и экспериментально в разделе квантовой оптики и квантовой информатики, называемой квантовой электродинамикой резонаторов (РКЭД) [1]. В последние годы предложено множество схем для генерации, управления контроля и защиты перепутывания кубитов раз-
личной физической природы в РКЭД-системах, таких как ионы в ловушках Пауля, нейтральные ридберговские атомы, сверхпроводящие джозеф-соновские кольца, электронные и ядерные спины в твердых телах, квантовые точки, азотозамещенные вакансии в алмазе, квантовые оптомеханические системы, гибридные квантовые системы [2–9]. Теоретические исследования различных систем РКЭД основаны на модели Джейнса – Каммингса (МДК) и ее обобщениях [10]. Многоатомные обобщения МДК часто в квантовой оптике и квантовой информатике называют моделями Тависа – Каммингса (МТК). Хорошо известно, что обобщения МТК, которые описывают взаимодействие естественных или искусственных двухуровневых атомов (кубитов) или многоуровневых атомов (кутриды, кудиты и т. д.) с выделенными модами различных резонаторов, позволяют описать все известные квантовые эффекты взаимодействия атомов с веществом [11–14]. В последнее время особое внимание уделялось изучению моделей типа Тависа – Каммингса с нелинейностями, в частности с керровской нелинейностью (см. библиографический список в [15–20]). Как известно
LM^^e © Башкиров Е.К., 2022
материал, показатель преломления которого пропорционален квадрату напряженности светового поля, называется средой Керра. Световой пучок, проходящий через такой материал, приобретает фазовый сдвиг ф = X т I , где X - постоянная Керра, τ – время взаимодействия светового поля с материалом и I – интенсивность луча. Эффект Керра широко используется в нелинейной квантовой оптике для генерации квадратурных и амплитудных сжатых состояний электромагнитного поля, параметрического преобразования частот, создания сверхбыстрых импульсов и т. д. Однако в оптическом диапазоне керровские нелинейности χ малы по сравнению со скоростью потери фотонов к из резонатора, что затрудняет использование данного эффекта для управления неклассическими состояниями света и атомов, в частности перепутыванием кубитов. Однако ситуация принципиально меняется для искусственных атомов в микроволновых резонаторах. В частности, для сверхпроводящих ожозефсоновских кубитов прямой аналог оптического эффекта Керра естественным образом создается за счет нелинейной индуктивности джозефсоновских контактов. Недавно такой эффект был использован для создания джозефсоновского параметрического усилителя [21]. В работе [22] удалось экспериментально реализовать режим однофотонного взаимодействия кубита с полем резонатора в среде Керра, соединив сверхпроводящий кубит (транзмон) в сапфировой среде с двумя трехмерными высокодобротными сверхпроводящими микроволновыми резонаторами. При этом удалось достичь значения постоянной Керра X /2 π =325 кГц, что по порядку величины совпадает со значение параметра кубит-фотонного взаимодействия в таких системах [5].
Хорошо известно, что взаимодействие квантовых систем с окружающей средой обычно оказывает разрушительное воздействие на такие свойства, как нелокальные квантовые корреляции подсистем или перепутывание. Однако в некоторых случаях взаимодействие с окружением может, напротив, приводить к перепутыванию подсистем. В частности к перепутыванию квантовых подсистем может приводить их взаимодействие с тепловым шумом. Возможность генерации перепутывания двух двухуровневых атомов c однофотонными переходами, взаимодействующих с тепловым полем резонатора, была впервые показана П. Найтом и соавторами [23]. Перепутывание в двухатомной системе с двухфотонным взаимодействием, инду- цированное тепловым шумом, было рассмотрено в работах [24-27]. Интересно отметить, что двухфотонное взаимодействие может значительно увеличить степень перепутывания атомов. Обобщение результатов работы [23] на случай нерезонансной двухатомной модели Джейнса – Каммингса было проведено в работе [28]. При этом автор показал, что включение расстройки может привести к существенному увеличению степени перепутывания кубитов. Кроме того, для системы двух кубитов с одно- и двухфотонными переходами, резонансно взаимодействующими с одномодовым тепловым полем, было показано, что степень перепутывания кубитов, индуцированная тепловым полем резонатора, сильно зависит от выбора их начального состояния [29; 30]. В частности, при наличии начальной когерентности состояний кубитов она приводит к увеличению степени их перепутывания. Представляет интерес рассмотреть особенности перепутывания кубитов для двухкубитной модели с нелинейностью другого типа, а именно керровской нелинейностью.
Недавно нами было исследовано влияние керровской нелинейности на динамику перепутывания двух кубитов, индуцированного тепловым шумом резонатора, в случае сепарабельных некогерентных [31] и перепутанных начальных состояний кубитов [32]. Представляет интерес обобщить результаты работы [31] на случай когерентных начальных состояний кубитов. Поэтому в настоящей работе мы исследуем влияние начальной атомной когерентности на динамику перепутывания двух идентичных кубитов, взаимодействующих с модой интенсивного теплового микроволнового электромагнитного поля идеального резонатора со средой Керра.
1. Модель и точное решение временного уравнения Шредигера
Рассмотрим два одинаковых сверхпроводящих кубита А ^ и A 2 , резонансно взаимодействующих с полем одномодового резонатора. Предположим, что константы связи между кубитами и полем резонатора равны. Предположим также, что в резонаторе имеется дополнительная среда Керра. Тогда гамильтониан взаимодействия для рассматриваемой системы в приближении вращающейся волны можно записать в виде
H = ^ й g ( g + a + g - a +) + й Xa + 2 a 2 , (1) i =1
где ст + =| + > ц < - 1 и ст - =| - > ii < + | - операторы переходов между возбужденным | + > i и основным состоянием | - > i в i -м кубите ( i = 1,2), a ˆ† и a ˆ – операторы рождения и уничтожения фотонов резонаторной моды, g – константа взаимодействия между кубитами и полем резонатора и X – константа нелинейности Керра.
Будем полагать, что в начальный момент времени кубиты приготовлены в сепарабельном, т. е. в не перепутанном состоянии. В самом общем виде такое начальное состояние кубитов можно представить в виде когерентной суперпозиции возбужденного и основного состояния:
| ^ (0) ) A = cos 0 1 | +) 1 + sin 0 1 | -) 1,
| ^ (0) ) A = cos 0 2 | +) 2 + sin 0 2 | -) 2,
где 01 и 02 — параметры, определяющие степень начальной когерентности кубитов A1 и A2 соответственно. Такие начальные состояния для есте- ственных или искусственных атомов (кубитов) можно получить в РКЭД с помощью микроволновых импульсов определенной длительности. Заме- тим, что, в отличие от оптики, мы под термином «когерентность», как это принято в РКЭД, понимаем наличие суперпозиции основного и возбужденного состояний кубита. Выбирая определенным образом параметры 01 и 02 , мы можем получить четыре некогерентных сепарабельных начальных состояния кубитов: | +, +), | +, -), | -, +), | -, -). Например, состоянию | +, -) соответствуют параметры 01=0 и 02 = п /2, а состоянию | +, +) соответствуют параметры 01 = 0 и 02 = 0.
Соответственно, полная начальная волновая функция системы кубитов есть
| W) ) A =| W) ) A^ ® | W) ) A . (3)
В качестве начального состояния поля выбе- рем одномодовое тепловое состояние с матрицей плотности вида
Р F ( 0 ) = T p n । n >< n |.
n
Весовые функции имеют здесь вид nn
Pn = n + 1 ’
( 1 + n )
где n - среднее число тепловых фотонов, определяемое формулой Бозе – Эйнштейна n = (exp [йю / квТ ]-1) , kB – постоянная Больцмана и T – температура микроволного резонатора. В зависимости от физической природы кубитов температура резона- тора может меняться от комнатных температур для азотозамещенных вакансий в алмазе до нК в случае нейтральных атомов и ионов в магнитных ловушках [5]. Поэтому в резонаторе всегда имеются тепловые фотоны.
Поставим перед собой задачу найти точную динамику подсистемы кубитов при наличии их взаимодействия с тепловым полем. Для решения поставленной задачи будем следовать схеме [33]. Начнем решение поставленной задачи в случае фоковских начальных состояний электромагнитного поля, а затем обобщим результаты на случай теплового поля. В случае фоковского начального состояния поля | Y(0))f =| n) (n = 0,1,2,...) состояние полной системы мы можем в любой момент времени задать с помощью волновой функции | Т(t))n, удовлетворяющей временному уравнению Шредингера вида iй d । ^(t))n = H | ^(t))n (4)
д t c начальным условием
| W) ) n =| ^ (0) ) A | n )
и стандартными для квантовой механики граничными условиями.
Формальное решение уравнения (4) можно представить в виде ˆ
| ¥ ( t ) ) n = e - iHt / ‘W) n . (5)
Эволюция волнового вектора | ^ ( t ) ) происходит в 4-мерном гильбертовом пространстве. Для начального состояния кубитов (2) и фоковского состояния поля | n ) в качестве базиса гильбертова пространтсва, в котором эволюционирует волновая функция системы, следует выбрать векторы вида
| - , - , n + 1 ) , | + , - , n ) , | - , + , n ) , | + , + , n - 1 ) .
При этом в случае n = 0 базис гильбертова пространства сужается до трех состояний вида | - , - ,1 ) , | + , - ,0 ) , | - , + ,0 ) .
Для нахождения явного вида вектора состояния (5) удобно использовать так называемые «одетые» состояния, т. е. собственные функции гамильтониана (1). В случае n >0 собственные функции имеют вид
| ^ in ) = w in ( C i 1 n | - , - , n + 1 )+ C i 2 n | + , - , n ) +
+ C i 3 n | - , + , n ) + C i 4 n | + , + , n - 1 ) ) (6)
( i = 1,2,3,4 ) , где
W in =1/ Vl C i 1 n Р + C i 2 n P + C i 3 n P + C i 4 n ,
C 11 n = -a 1 n / Y 1 n , C 12 n = ^ 1 n + в 1 n / 5 1 n ,
C 13 n = -в 1 n / 5 1 n , C 14 n = 1,
C 21 n = -(a 2 n + nE 2 n ) / Y 2 n ,
C 22 n = E 2 n + в 2 n / 5 2 n ,
C 23 n = -в 2 n / 5 2 n , C 24 n = 1,
C 31 n = -(a 3 n + nE 3 n ) / Y 3 n ,
C 32 n = E 3 n + в 3 n / 5 3 n ,
C 33 n = -в 3 n / 5 3 n , C 34 n = 1,
C 41 n = 0, C 42 n = - 1, C 43 n = 1, C 44 n =0
и a in = -2X + n X + 2 n 2x - n3 x + Ein,
P in = 2 X - n X- n 2 X + 2 n 3 X - E in - 2 nEin ,
Y in = T n 7 n + 1( n X + n 2 X — E 1 n ),
-
5 in = V n ( - n 2 X 2 + n 4 X 2 - 2 n 2 X E 1 n + E 1 2 n ) , X in = - (2 X - 3 n X + n 2 X - E 1 n ) / T n .
и X = X / Y . Соответствующие собственные значения энергии есть
-
E 1 n / Й g =
= A
n
+ Re
2 B n
_ 3 ( D n + F n Г
+ 1 ( D n + F n ) 1/3
E 2 n / Й g = A n - Re
( 1 + i V3 ) B n +
3 ( D n + F n ) 1/3
+ 1 ( - 1 + i T3 ) ( D n + F n ) 1/3
E 2 n / Й g = A n - Re
( 1 - i V3 ) B n
3 ( D n + F n ) 1/3
F =- J-32 A 3 + C .
n 2 nn
Для случая n =0 собственные функции есть
| У ( 0) > 1 = (1 / 2)( - V2 | - , - , 1 )+ | + , - , 0 )+ | - , + , 0 ) ,
I У ( 0) > 2 = (1 / 2)(V2 | - , - , 1 >+ | + , - , 0 )+ | - , + ,0 > , (7)
| У ( 0) > 3 =(1/V2(| + , - ,0 >- I - , + ,0 > ).
Соответствующие значения энергии e10) / йg = -2, E20)/ Йg = 2, E30)/ Йg = 0.
Теперь для нахождения явного вида волновой функции (5) достаточно выразить начальный вектор состояния через собственные функции гамильтониана (1). Выполним это действие для начального состояния вида | У (0) > =| + , - , n > в случае n >0. Имеем
* *
| + , - , n > = C 12 n | У 1 n > + C 22 n | У 2 n > +
+ C 32 n । У 3 n > + C 42 n । У 4 n >
Подставляя (8) в правую часть формулы (5), получаем окончательно явный вид временной волновой функции в случае начального состояния | + , - , n >
| У ( t ) > n = Z 12,n | - , - , n + 1 > + Z 22, n | + , - , n > +
-
+ Z 32, n | - , + , n > + Z 42, n | + , + , n >, где
-
-iE. t/Й*
1n i2,n 1n i2n 1in
-
-iE„ t / Й * -iE„ t/Й
+ e n w 2 n C i 2 n C 2 in + e n w 3 n C i 2 n C 3 in +
-
- iE t/Й
+ e n w 4 n C i 2 n C 4 in
( i = 1,2,3,4).
Для случая n =0 временная волновая функция имеет, соответственно, вид
(0) (0) (0)
| У ( t ) > 0 = Z 12 | - , - , 1 >+ Z 22 | + , - ,0 >+ Z 32 | - , + ,0 > , (10)
- 6 ( 1 + i V3 ) ( D n + F n ) 1/3
E4n / Йg = (-n + n2 )x, где
A n = 3(2 + 3( - 1 + n ) n ) X ,
B n = ( 3 + 6 n + 2(1 + 3( - 1 + n ) n ) x 2 ) ,
C n = 64 ( 9( - 1 + n ) x + (2 + 9( - 1 + n ) n ) x 3 ) 2 , D n = - 36 x + 36 n X + 8 X 3 - 36 n X 3 + 36 n 2 X 3 ,
где
Z 10) = - i sin ( V2 Y t ) /72, Z 20) = cos 2 ( y t /72 ) ,
Z 30) = - sin 2 ( y t /72 ) .
Аналогичным образом мы можем найти временную волновую функцию полной системы для начального состояния кубитов вида | + , + , n - 1 > , | - , + , n > и | - , - , n + 1 > . Для указанных состояний в случае n > 0 временные волновые функции будут иметь вид (9) при замене Z i2 n на Z^n , Z^n и Zi 1 n соответственно. Для начального состояния | - , + ,0 > временная волновая функция системы принимает вид
(0) (0)(0)
I т(t))o = Z13 | -, -, 1) + Z23 | +, -,0; + Z33 1 -, +,0), где
(0) (0) (0) (0) (0)(0)
Z 13 = X 12, Z 23 = Z 22, Z 33 = X 32.
Для начального состояния | -, -,1) временная волновая функция есть (0) (0)(0)
Psi(t)) = Z^ | -,-,1) + Z24 1 +,-,0) + Z34 1 -,+,0),
2 1*4 ( t ) = e - (1/2) i ( а- 2 5 ) t ( (8 + ( а + 2 5 ) 2 ) cos( Q t / 2) +
+ ( а + 2 5 ) Q i sin( Q t /2) ) / Q 2 ,
—it ( а- 2 5 )
Z 24 ( t ) = Z 34 ( t ) = - 2 ie 2 sin( Q t /2)/ Q .
Наконец, для начального состояния | - , - ,0 ) имеем | ^ ( t ) ) =| - , — ,0 ) . (13)
Комбинируя выражения (6)-(13), мы легко можем получить временную волновую функцию полной системы для когерентных начальных состояний кубитов. Явное выражение для временной волновой функции здесь не приводится ввиду его громоздкости.
В случае теплового начального состояния поля и начального состояния кубитов (2) временная матрица плотности полной системы удовлетворяет квантовому уравнению Лиувилля i = [ H, р( t)]
d t c начальным состоянием вида р(0) =| ^(0))AA <^(0) | ® ®Р F (0).
Формальное решение уравнения Лиувилля может быть представлено в виде
р ( t ) = e - iHt / й р (0) e + iHt / к =
= e - iHt/ к । ^ (0) ) AA (^ (0) | ® р F (0) e + iH / к =
= £ P n e - iHt / ' । ^ (0) ) AA <^ (0)I e + iHt / * = (14)
n =0
= £ P n I * ( t ) ) n <^ ( t )|.
n =0
Подставляя в (14) найденные волновые функции | T ( t ) ) n для соответствующих некогерентных сепарабельных начальных состояний кубитов или комбинации таких функций для когерентного начального состояния кубитов, мы можем получить точное выражение полной матрицы плотности изучаемой модели. Окончательное выражение для полной матрицы плотности не приводится ввиду его громоздкости.
Полученное точное решение может быть использовано для получения временных зависи- мостей любых наблюдаемых для подсиcтемы кубитов и резонаторного поля. В качестве иллюстрации возможного применения полученного точного решения для полной матрицы плотности рассматриваемой задачи используем указанное решение для нахождения временной зависимости параметра перепутывания кубитов. Для решения поставленной задачи нам необходимо получить из полной матрицы плотности р(t) редуцированную двухкубитную матрицу плотности. Для этого необходимо усреднить полную матрицу плотности по переменным поля
^
Р A ( t ) = Tr F Р ( t ) = ^ < n I р ( t ) | n ) .
n =0
Удобно записать р A ( t ) в матричной форме, используя двухкубитный базис
1 - , -) , 1 + , -) , 1 - , +) , 1 + , +) ,
|
р 11 |
р 12 |
р 13 |
р 14 |
|
|
р 12 |
р 22 |
р 23 |
Р 24 |
|
|
РА ( t ) = A |
. * |
* |
||
|
р 13 |
р 23 |
р 33 |
Р 34 |
|
|
* (Р 14 |
* р 24 |
* р 34 |
Р 44 у |
Нами найдены явные выражения для элементов редуцированной матрицы плотности, однако здесь они не приводятся ввиду их громоздкого вида.
2. Динамика перепутывания кубитов
Для двухкубитной системы, описываемой матрицей атомной плотности р A ( t ), мера перепутывания или отрицательности может быть определена в терминах отрицательных собственных значений ц- частично транспонированной редуцированной атомной матрицы плотности ( р А 1) для (15) s = - 2 ^ ц- . (16)
В случае когда s = 0, два кубита являются сепарабельными (т. е. они не перепутаны), а условие s > 0 означает наличие атом-атомного перепутывания. Случай s = 1 указывает на максимальное перепутывание .
Результаты численного моделирования временной зависимости отрицательности (16) для теплового состояния поля резонатора представлены на рис. 1, 2. Безразмерный параметр керровской нелинейности для кривых, представленных на рисунках, выбран равным j( = 1. В качестве начальных состояний кубитов выбраны состояния: некогерентное состояние | Y (0) ) A = | + , -) (штриховая линия) и когерентное состояние | Y (0) ) A 1 =
£(t)
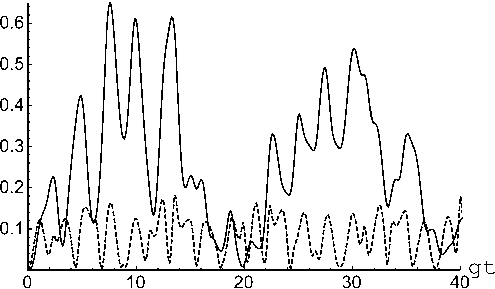
Рис. 1. Временная зависимость отрицательности от безразмерного времени gt в случае начального состояния кубитов | + , -〉 (штриховая линия) и когерентного состояния (2) c θ 1 = π /4 и 0 2 = -п /4 . Безразмерный параметр керровской нелинейности X = 1 . Среднее число тепловых фотонов n = 0 , 5
Fig. 1. Time dependence of negativity on dimensionless time gt in the case of the initial state of qubits | + , -〉 (dashed line) and coherent state (2) with 0 1 = п /4 and 0 2 = -п /4 . Dimensionless parameter of the Kerr nonlinearity X = 1 - Average number of thermal photons is n = 0 , 5
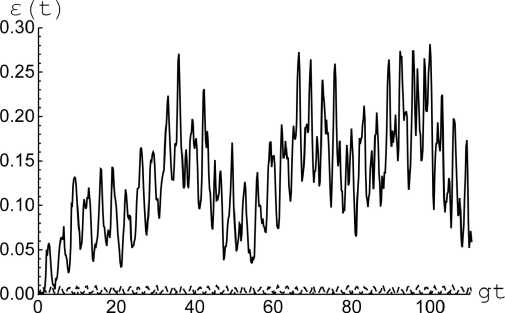
Рис. 2. Временная зависимость отрицательности от безразмерного времени gt в случае начального состояния кубитов | + , -〉 (штриховая линия) и когерентного состояния (2) c θ 1 = π /4 и 0 2 = -п / 4 . Безразмерный параметр керровской нелинейности X = 1 . Среднее число тепловых фотонов n = 20
Fig. 2. Time dependence of negativity on dimensionless time gt in the case of the initial state of qubits | + , -〉 (dashed line) and coherent state (2) with 0 1 = п /4 and 0 2 = -п /4 . Dimensionless parameter of the Kerr nonlinearity X = 1 . Average number of thermal photons is n =20
= (1/ 2)(| +〉 2 +〉 2) 〉 , | Ψ (0) 〉 A 2=(1/ 2)(| +〉 2 - | -〉 2) 〉 (сплошная линия). Вычисления проведены для случая теплового поля резонатора с n = 0,5 (рис. 1) и n = 20 (рис. 2). Из рисунков хорошо видно, что при наличии керровской нелинейности начальная атомная когерентность приводит к существенному увеличению степени перепутывания кубитов даже для интенсивных тепловых полей резонатора. Таким образом, приготовив кубиты в когерентном начальном состоянии, мы можем добиться существенного увеличения степени их перепутывания.
Заключение
Таким образом, в настоящей работе мы нашли точное решение уравнения эволюции для двухку- битной модели Тависа – Каммингса с керровской нелинейностью и тепловым полем резонатора для когерентного начального состояния кубитов. Полученное точное решение использовано для анализа временной динамики перепутывания кубитов, индуцированного тепловым полем резонатора. Показано, что для модели с керровской нелинейностью наведение начальной когерентности кубитов приводит к существенному увеличению максимальной степени перепутывания кубитов даже в случае интенсивного теплового поля резонатора. Полученные результаты могут быть полезны при выборе оптимальных режимов функционирования квантовых устройств, таких как квантовые компьютеры и квантовые сети.
Список литературы Перепутывание двух сверхпроводящих кубитов, индуцированное тепловым шумом резонатора со средой Керра, при наличии начальной атомной когерентности
- Dutra S.M. Cavity Quantum Electrodynamics: The Strange Theory of Light in a Box. Hoboken: John Wiley & Sons, 2005. 389 p. DOI: https://doi.org/10.1002/0471713465
- Buluta I., Ashab S., Nori F. Neutral and artificial atoms for quantum computation // Rep. Prog. Phys. 2011. Vol. 74, no. 10. P. 104401. DOI: https://doi.org/10.1088/0034-4885/74/10/104401
- Cavity quantum electrodynamics / H. Walther [et al.] // Rep. Prog. Phys. 2006. V. 69. P. 1325–1382. DOI: https://doi.org/10.1088/0034-4885/69/5/R02
- Quantum dynamics of single trapped ions / D. Leibfried [et al.] // Rev. Mod. Phys. 2003. Vol. 75. P. 281–324. DOI: https://doi.org/10.1103/RevModPhys.75.281
- Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems / Z.-L. Xiang [et al.] // Rev. Mod. Phys. 2013. Vol. 85. P. 623–653. DOI: https://doi.org/10.1103/RevModPhys.85.623
- Georgescu I.M., Ashhab S., Nori F. Quantum simulation // Rev. Mod. Phys. 2014. Vol. 88. P. 153–186. DOI: https://doi.org/10.1103/RevModPhys.86.153
- Microwave photonics with superconducting quantum circuits / X. Gu [et al.] // Phys. Repts. 2017. Vol. 718–719. P. 1–102. DOI: https://doi.org/10.1016/j.physrep.2017.10.002
- Wendin G. Quantum information processing with superconducting circuits: a review // Rep. Prog. Phys. 2017. Vol. 80. P. 106001. DOI: https://doi.org/10.1088/1361-6633/aa7e1a
- Li G.-Q., Pan X.-Y. Quantum information processing with nitrogen–vacancy centers in diamond // Chinese Physics. 2018. Vol. 27, no. 2. P. 020304. DOI: https://doi.org/10.1088/1674-1056/27/2/020304
- Jaynes E.T., Cummings F.W. Comparison of quantum and semiclassical radiation theory with application to the beam maser // Proc. IEEE. 1963. Vol. 51, no. 1. P. 89–109. DOI: https://doi.org/10.1109/PROC.1963.1664
- Shore B.W., Knight P.L. The Jaynes–Cummings model // J. Mod. Opt. 1993. Vol. 40. P. 1195–1238. DOI: https://doi.org/10.1080/09500349314551321
- Larson J. Dynamics of the Jaynes–Cummings and Rabi models: Old wine in new bottles // Physica Scripta. 2007. Vol. 76. P. 146–160. DOI: https://doi.org/10.1088/0031-8949/76/2/007
- Quantum correlations between light and the kilogram-mass mirrors of LIGO / H. Yu [et al.] // Nature. 2020. Vol. 583, no. 12. P. 43–47. DOI: https://doi.org/10.1038/s41586-020-2420-8
- Dai H., Fu S., Luo S. Atomic nonclassicality in the Jaynes-Cummings model // Phys. Lett. A. 2020. Vol. 384, no. 12. P. 126371. DOI: https://doi.org/10.1016/j.physleta.2020.126371
- Puri S., Boutin S., Blais A. Engineering the quantum states of light in a Kerr-nonlinear resonator by two-photon driving // Quantum Information. 2017. Vol. 3, no. 1. P. 18. DOI: https://doi.org/10.1038/s41534-017-0019-1
- Effects of Kerr medium in coupled cavities on quantum state transfer / A.F. Al Naim [et al.] // J. Nonlin. Opt. Phys. Mater. 2018. Vol. 27, no. 3. P. 1850035. DOI: https://doi.org/10.1142/S0218863518500352
- Effects of Kerr medium and Stark shift parameter on Wehrl entropy and the field puruty for two-photon Jaynes–Cummings model under dispersive approximation / A.F. Al Naim [et al.] // J. Rus. Las. Res. 2019. Vol. 40, no. 1. P. 20‒29. DOI: https://doi.org/10.1007/s10946-019-09764-w
- Anwar S.J., Ramzan M., Khan M.K. Effect of Stark- and Kerr-like medium on the entanglement dynamics of two three-level atomic systems // Quant. Inform. Process. 2019. Vol. 18, no. 6. P. 192. DOI: https://doi.org/10.1007/s11128-019-2277-7
- Аданмитонде А.Ж, Авосву Г.И.Ю., Доса Ф.А. О квантовании некоторых обобщенных моделей Джейнса – Каммингса в керроподобной среде // Теор. матем. физ. Физ.-мат. науки. 2020. Т. 203, № 3. С. 451–466. DOI: https://doi.org/10.4213/tmf9835
- Aldaghfag S.A., Berrada K., Abdel-Khalek S. Entanglement and photon statistics of two dipole-dipole coupled superconducting qubits with Kerr-like nonlinearities // Results in Phys. 2020. Vol. 16. P. 102978. DOI: https://doi.org/10.1016/j.rinp.2020.102978
- Phase-preserving amplification near the quantum limit with a Josephson ring modulator / N. Bergeal [et al.] // Nature. 2010. Vol. 465, no. 7294. P. 64–68. DOI: https://doi.org/10.1038/nature09035
- Observation of quantum state collapse and revival due to the single-photon Kerr effect / G. Kirchmair [et al.] // Nature. 2013. Vol. 495, no. 7440. P. 205–209. DOI: https://doi.org/10.1038/nature11902
- Entanglement induced by a single-mode heat environment / M.S. Kim [et al.] // Phys. Rev. A. 2002. Vol. 65, no. 4. P. 040101. DOI: https://doi.org/10.1103/PhysRevA.65.040101
- Zhou L., Song H.S. Entanglement induced by a single-mode thermal field and criteria for entanglement // J. Opt. B. 2002. Vol. 4, no. 6. Р. 425–429. DOI: https://doi.org/10.1088/1464-4266/4/6/310
- Bashkirov E.K. Entanglement induced by the two-mode thermal noise // Laser Phys. Lett. 2006. Vol. 3, no. 3. P. 145–150. DOI: https://doi.org/10.1002/lapl.200510081
- Bashkirov E.K., Stupatskaya M.P. The entanglement of two dipole-dipole coupled atoms induced by nondegenerate two-mode thermal noise // Laser Phys. 2009. Vol. 19, no. 3. P. 525–530. DOI: https://doi.org/10.1134/S1054660X09030281
- Bashkirov E.K., Mastyugin M.S. The influence of the dipole-dipole interaction and atomic coherence on the entanglement of two atoms with degenerate two-photon transitions // Opt. Spectr. 2014. Vol. 116, no. 4. P. 630–634. DOI: https://doi.org/10.1134/S0030400X14040067
- Zhang B. Entanglement between two qubits interacting with a slightly detuned thermal feld // Opt. Commun. 2010. Vol. 283, no. 23. P. 4676–4679. DOI: https://doi.org/10.1016/j.optcom.2010.06.094
- Coherence-enhanced entanglement between two atoms at high temperature / Y.-H. Hu [et al.] // Chin. Phys. B. 2008. Vol. 17, no. 5. P. 1784–1790. DOI: https://doi.org/10.1088/1674-1056/17/5/039
- Башкиров Е.К., Мангулова Е.Г. Перепутывание атомов, индуцированное двухмодовым тепловым шумом, при наличии диполь-дипольного взаимодействия и атомной когерентности // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2013. Т. 2, № 31. С. 177–184. DOI: https://doi.org/10.14498/vsgtu1160
- Evseev M.M., Bashkirov E.K. Thermal entanglement in Tavis–Cummings model with Kerr nonlinearity // 2020 International Conference on Information Technology and Nanotechnology (ITNT). 2020. P. 9253347. DOI: https://doi.org/10.1109/ITNT49337.2020.9253347
- Bashkirov E.K. Entanglement in Tavis–Cummings model with Kerr nonlinearity induced by a thermal noise // Proc. SPIE. 2021. Vol. 11846. P. 210–219. DOI: https://doi.org/10.1117/12.2588673
- Bashkirov E.K. Entanglement of two dipole-coupled qubits interacting with a detuned cavity thermal field // Proc. SPIE. 2019. Vol. 11066. P. 115–121. DOI: https://doi.org/10.1117/12.2522476


