Перепутывание между атомом, взаимодействующим с тепловым полем идеального резонатора, и свободным атомом

Перепутанные состояния составляют фундамент квантовой информатики, физики квантовых вычислений, квантовых коммуникаций и квантовой криптографии [1]. В настоящее время предложены различные способы генерации перепутывания естественных и искусственных атомов (охлажденных ионов или нейтральных атомов в резонаторах, сверхпроводящих джо-зефсоновских цепей, спинов в твердых телах, квантовых точек и др.) [2]. В частности такое перепутывание может возникать за счет взаимодействия атомов с квантовыми полями резонаторов.

Для оптимальной работы квантовых устройств требуются максимально перепутанные состояния. Однако любая квантовая система взаимодействует с окружающей средой, что обычно приводит к декогеренции. Однако недавно было показано, что взаимодействие квантовых систем с окружением может приводить к их перепутыванию [3]. В частности, Ким и соавторы. [4] исследовали атом-атомное перепутывание в системе двух одинаковых двухуровневых атомов с однофотонным переходами, резонансно взаимодействующих с одномодовым тепловым полем. Они показали, что хаотическое поле, ха- рактеризующееся минимумом информции, может перепутать атомы, подготовленные первоначально в сепарабельном состоянии. Дзенг [5] обобщил результаты работы [4] на случай, когда частота атомного перехода слегка отстроена от частоты моды теплового поля. Он показал, что небольшая расстройка атомов и поля может привести к существенному увеличению степени перепутывания. В работах [6; 7] было показано, что нелинейное взаимодействие теплового поля c атомами в резонаторе также может приводить к атом-атомному перепутыванию. Влияние ди-поль-дипольного взаимодействия на перепутывание атомов, резонансно взаимодействующих с тепловыми полями резонатора, изучалось в работах [8–11]. В наших работах [12; 13] показана возможность перепутывание двух дипольносвязанных идентичных атомов, один из которых резонансно взаимодействует с модой теплового поля, а другой может свободно перемещаться вне резонатора. Представляет интерес обобщить результаты указанных работ на случай нерезонансного взаимодействия атома с полем резонатора. Поэтому в настоящей работе нами поставлена задача изучения влияние расстройки на особенности перепутывание атомов в рамках модели, описанной в [12; 13].

1.    Модель и ее точное решение

Рассмотрим два идентичных двухуровневых естественных или искусственных атома. Пусть один из атомов нерезонансно взаимодействует с модой теплового поля в идеальном одномодовом резонаторе, а второй находится вне резонатора. Предположим также, что между атомами имеется эффективное диполь-дипольное взаимодействие. Заметим, что для некоторых типов искусственных атомов, например для сверхпроводящих джозефсоновских кубитов, эффективная константа диполь-дипольного взаимодействия может значительно превосходить константу атом-полевого взаимодействия. Тогда в системе отсчета, вращающейся с частотой поля to, гамильтониан рассматриваемой системы в приближении вращающейся волны можно записать в виде

H = ЙЛо z + ЙЛо z +

• ^{1        2}                                         (1)

+ Й у(с + a + a ⁺G 1 ) + h J (o + O + О O + ).

Здесь o z и o z — операторы инверсии двух атомов; о + = | +) а (- | и о - = | -) а (+ | — повышающий и понижающий операторы и | +) i и | -) i — возбужденное и основное состояние i -го двухуровневого атома ( i = 1,2); а ⁺ и a — операторы рождения и уничтожения фотонов резонаторной моды; у — константа атом-полевого взаимодействия; Л — расстройка частот атома и поля Л = to o - to, где to o — частота перехода в двухуровневом атоме. Наконец, J – эффективная константа диполь-дипольного взаимодействия.

Будем полагать, что в начальный момент времени атомы приготовлены в сепарабельном двухатомном состоянии вида

| W)) а =|+, -),                                  (2)

а поле резонатора находится в тепловом состоянии с матрицей плотности

Р F (0) = ^ p n | П X П |,                           (3)

n где вероятности pn = nn / (1 + n)n+1. Здесь n — среднее число фотонов в резонаторной моде n = = (exp[fttoi / kBT] - 1] 1, где кв — постоянная Больцмана и T – равновесная температура резонатора.

Прежде чем исследовать случай, когда атом взаимодействует с тепловым полем, рассмотрим предварительно более простую ситуацию, в которой резонаторное поле приготовлено в фо-ковском состоянии. Предположим, что число возбуждений системы «атомы+поле» равно n

( n > 0). В этом случае эволюция системы будет происходить в в гильбертовом пространсте с базисом | -, -, n + 2), | +, -, n + 1), | -, +, n + 1), | +, +, n ). Тогда собственные векторы гамильтониана (1) могут быть записаны как

| ^ in ⁾ = w in ⁽ X i 1 n | -, ^-, ^{n + 2) +}

⁺ X i 2 n | ⁺, ^-, ^{n + 1 +} X i 3 n | ^-, ⁺, ^{n + 1 +          (4)}

+ Xi4n | +, +, n))   (i = 1,2,3,4), где win =

= 1/V| X i 1 n ²

⁺ | X i 2 n 2 ⁺ | X i 3 n 2 ⁺ | X i 4 n 2

и

V2 + n (1 + n + 25Ein - Ein ) V1 + n a(25 + Ein)

X i 2, n

1 + n + 25Ein - Ein V1 + n a

Xs = -i 3, n

25 - Ein yj 1 + n

X i 4, n = 1.

Соответствующие собственные значения гамильтониана (1) есть

E _ln = D_n - F „, E _2n = D „ + F „, nnn nnn

E _3n = - D„ - F ,   E _4n = - D „ + F ,

3nnn4nnn где

^D n = 2V3 ^² B n + G n

F n

1    _{4 B}

23 ⁿ

- G n - 45Vs / 72 B n + G n ,

A n = 2 + 3 n + n ² + 4a²5²,

Bn = 3 + 2 n + a2 + 452,

G n

C n

O n

= 2^1/3 ( 12 A n + B² n ) / C n + C n /2^1/3. = ( 72 A _n B _n + 2 B n + 1085² + O n ) 1 ^/3 ,

-4 (12 An + Bn )3 + (72 AnBn + 2 Bn + 10852 )2, где 5 = Л / у, a = J / y.

Предположим, что рассматриваемая система в начальный момент времени приготовлена в состоянии | +, -, n + 1) (n > 0). Тогда временную волновую функцию в момент времени t можно записать в виде

| ^⁽ t ⁾⁾ = C 12, n | ^-, ^-, ^{n + 2) +} C 22, n | ⁺, ^-, ^{n + 1 +}

+ C32,n | -, +, n + 1) + C42,n | +, +, nX где

C i 2, n = e - iE1 n t / ^Й W 1 n Y 2 in X 1 in +

• -    iE- t /Й    _TZ

⁺ e        ^w 2 n Y 2 in ^X 2 in ⁺

+ e ^- iE ³ n t ^{/ Й} W 3 n Y 2 in X 3 in +                       (7)

• -    iE. t /Й     _{Tr XT}

⁺ e        ^w 4 n ^Y 2 in ^X 4 in

( i = 1,2,3,4)

и Y jn = W jn X *in .

Если начальное состояние изучаемой системы выбрать в виде | +, -, 0), то временная волновая функция есть

| Y( t )) = C 12 |-, -1) +

⁺ C 22 | ⁺, ^-, ^{0) +} C 32 | ^-, ⁺, ⁰⁾,

Ei £ t sje j / qj, j=1

i i s t

C22 =/(2sj5-s2)e j / qj, j=1

i t

C32 = -a//28 - sj)e    / qj j=1

где qj = 1 + a — 3s j + 4s j 8,

- I3W+

3 (   ^     3 2

-

_ 1 f ( 1 + i V3 ) z ( 1 - i V3 ) ^

^s 2 = 3

2^2/3 §        2 3 2

V

-

_s = 1 f ( 1 - i Уа ) z ( 1 + i У3 ) ^

) +28,

)

+28 •

2 2/3 ^

§ = 3 ^( -36a²8 + 168 3 + 188 ) 2 +

+ 4 ( -3a² - 48² - 3 ) 3 - 36a²8 + 168 3 + 188, Z = -3a² - 48² - 3.

Выберем теперь начальное состояние в виде | -, +, n + 1) (n > 0). В этом случае в произвольный момент времени вектор состояния есть

¹ ^⁽ t ⁾⁾ = C 13, n ^{1 -}, ^-, ^{n + 2) +} C 23, n ^{1 +}, ^-, ^{n + 1 + +} C 33, n | ^-, ⁺, ^{n + 1) +} C 43, n | ⁺, ⁺, ^{n )},

где C _{i 3, n} могут быть получены из (7) путем за^мены Y 2in ^{на Y} 3 in ⁽ i = 1, ², ³, 4).

Если начальное состояние есть | -, +, 0), то зависящая от времени волновая функция примет вид

| Y( t )) = C 13 |-, -,1) +

⁺ C 23 | ⁺, ^-, ^{0) +} C 33 | ^-, ⁺, ⁰⁾,

C 13	3 i s t = -a / e j j = 1 3	/ q j ,
C 23	= a / (28-	i s s j ) e ■
	j = 1
C 33	3 i s t = -a / e j	/ q j .

t

1 / qj, j=1

Для начальных состояний | +, +, n ) и | -, -, n + 2) ( n > 0) временные волновые функции соответственно равны

| ^⁽ t ⁾⁾ = C 11, n | ^-, ^-, ^{n + 2) +} C 21, n | ⁺, ^-, ^{n + 1 +}

⁺ C 31, n | ^-, ⁺, ^{n + 1) +} C 41, n | ⁺, ⁺, ^{n )}.

| ^⁽ t ⁾⁾ = C 14, n | ^-, ^-, ^{n + 2) +} C 24, n | ⁺, ^-, ^{n + 1 +}

14, n                   24, n                 (12)

⁺ C 34, n | ^-, ⁺, ^{n + 1) +} C 44, n | ⁺, ⁺, ^{n )}.

Коэфициенты C _{i 1, n} (или C _{i 4, n} ) могут быть получены из (7) путем замены Y _{2 in} на Y _{1 in} (или Y _{4 in} ) ( i = 1, 2, 3, 4).

Для начальногог состояния | -, +,1) эволюция системы задается волновой функцией

| Y( t )) = C 14 |-, -,1) +

⁺ C 24 | ⁺, ^-, ^{0) +} C 34 | ^-, ⁺, ⁰⁾,

где

C14 = ^(a2 -s2)eiS1)t / qj, j=1

C24 = ^s je 1 / qj, j=1

i s _j t

^C 34 = ^-a / e ^J / q j .

j = 1

Наконец, для начальногго состогяния | -, -, 0) имеем

| ^( t )) = exp[- i (28 1 ]|-, -,0). (14)

Используя выражения (4)–(14), мы легко можем вычислить временную матрицу плотности p( t ) всей системы. Усредняя p( t ) по переменным поля, мы можем вычислить редуцированную атомную матрицу плотности р a ( t ) = Tr F р( t ). Явные выражения для полной матрицы плотности р( t ) и редуцированной атомной матрицы плотности р a ( t ) не приведены здесь из-за их громоздкого вида.

2.    Вычисление отрицательности

Для двухкубитных систем, описываемых редуцированной матрицей плотности р a ( t ), в качестве меры перепутывания может быть использована отрицательность [15; 16]

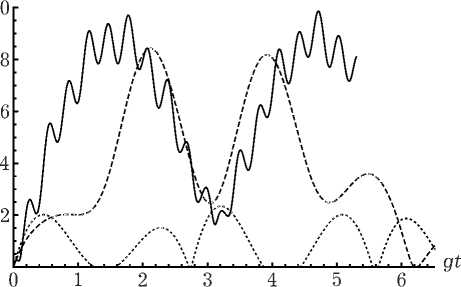
Рис. 1. Отрицательность как функция безразмерного времени у t для различных значений параметра расстройки 6 = 0 (сплошня линия), 6 = 1 (штриховая линия) и 6 = 5 (точечная линия). Параметр диполь-дипольного взаимодействия а = 0.5. Среднее число фотонов n = 0.1

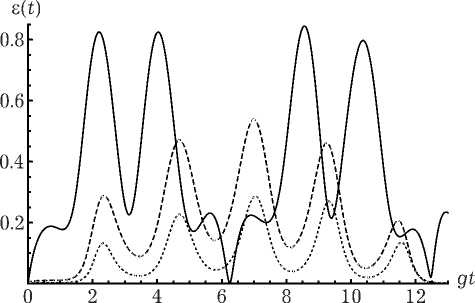
Рис. 2. Отрицательность как функция безразмерного времени у t для различных значений параметра диполь-диполь-ного взаимодействия а = 0.05 (сплошная линия), а = 0.1 (штриховая линия) и а = 0.5 (точечная линия). Расстройка 6 = 0.9. Среднее число фотонов n = 0.1

eW

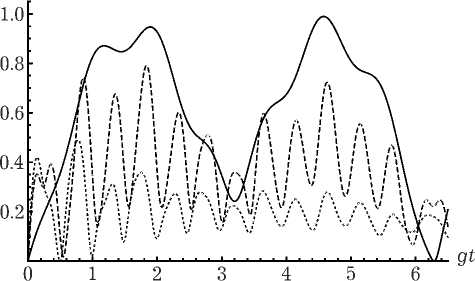
Рис. 3. Отрицательность как функция безразмерного времени y t для различных значений среднего числа тепловых фотонов n = 0 (точечная линия), n = 1 (штриховая линия) и n = 5 (сплошная линия). Расстройка 6 = 3. Параметр ди-поль-дипольного взаимодействия а = 0.5

е = -2^ц -, где цI — отрицательные собственные значения частично транспонированной атомной матрицы T плотности (рAJ.

Для сепарабельного начального атомного состояния (2) и поля в тепловом состоянии (3) редуцированная атомная матрица плотности имеет вид

"р11( t) 0 0 0 1 0 р22(t) р23(t) 0 р A (t) = .          (15) 0 р23(t) рзз(t) 0 . 0 0 0 р44 (t) J Элементы матрицы плотности (16) можно запи- сать в виде да р11 = Epn I C42,n-1(t) |2, n=0 да р22 = Epn | C22,n-1(t) |2 + p0C22(t), n=0

да р33 = Epn 1 C32,n-1(t) 2 + p0C32(t), n=0

да р44 = EPn | C12,n(t) |2 + P0C12(t), n=0

да р23 = E PnC22, n—1( t) C32, n-1( t )*.

n = 0

Частично транспонированная по переменным одного кубита по отношению (15) матрица р A есть

	р 11 ( t )	0	0	р 23 ( t )
T р д( t ) =	0	р 22 ( t )	0	0	.         (16)
	0	0	р зз ( t )	0
	(р 23 ( t )	0	0	р 44 ( t ) у

Матрица (16) имеет всего одно собственное значение, которое может быть отрицательным. Соответственно отрицательность для рассматриваемых начальных атомных состояний может быть представлена в виде

s⁽ t ) = V(^рй( t ^)—р 44 ( t ))²⁺⁴f^р 2з C t )l^{2 -}

^{- р} 11 ⁽ t ) ^{- р} 44 ⁽ t ).

Результаты численных расчетов отрицательности (17) для различных параметров модели с гамильтонианом (1) представлены на рис. 1–3.

3.    Результаты и обсуждения

Временные зависимости отрицательности для различных значений параметра расстройки приведены на рис. 1. Кривые построены для фиксированных значений среднего числа тепловых фотонов n = 0.1 и нормированной константы диполь-дипольного взаимодействия а = 0.5. Из рисунка хорошо видно, что при увеличении параметра атом-полевой расстройки 5, степень перепутывания атомов существенно возрастает. Отметим, что в отличие от двуатомной модели с общим полем резонатора, для рассматриваемой модели атомное перепутывание возникает только при наличии диполь-дипольного взаимодействия. Зависимость отрицательности от нормированного времени gt для различных значений параметра диполь-дипольного взаимодействия а представлена на рис. 2. При этом среднее число фотонов выбрано равным n = 0.1, а параметр расстройки 5 = 0.9. Хорошо видно, что с увеличением интенсивности диполь-дипольного взаимодействия степень атомного перепутывания возрастает. Такой результат не является удивительны для начального состояния атомов вида | +, -). Такое поведение параметра атомного перепутывания для указанного начального состояния характерно и для моделей с общим полем резонатора [8–11] . На рис. 3 представлена временная зависимость отрицательности для различных значений среднего числа фотонов в тепловой моде и фиксированных значений интенсивности диполь-дипольного взаимодействия а = 0.5 и расстройки 5 = 3. Из рисунка хорошо видно, что при увеличении интенсивности теплового поля, степень перепутывания атомов уменьшается. Это означает, что значительного перепутывания атомов можно добиться только для слабого теплового поля резонатора, т. е. при достаточно низких температурах резонатора Заметим, что максимальная степень атомного перепутывания для рассматриваемо модели меньше, чем для модели, в которой два атома взаимодействуют с общим тепловым полем резонатора в случае одинаковых интенсивногстей теплового поля [5].

Заключение

Таким образом, в настоящей работе мы исследовали динамику перепутывания двух идентичных двухуровневых атомов, один из которых нерезонансно взаимодействует с модой теплового поля идеального одномодового резонатора, а другой находится вне резонатора. Мы обсудили влияние диполь-дипольного взаимодействия и расстройки на степеннь перепутывания атомов для сепарабельного исходного атомного состояния. При этом было показано, что атом-атомное перепутывание возникает только при наличии прямого диполь-дипольного взаимодействия атомов. Мы также показали, что наличие расстройки частот атома и поля приводит к существенному увеличению степени атомного перепутывания. Увеличение параметра расстройки и интенсивности прямого диполь-дипольного взаимодействия приводит к увеличению максимальной степени перепутывания атомов. Таким образом, расстройка и прямое диполь-диполь-нгое взаимодействие в рассматриваемой модели могут быть использованы для эффективного управления и контроля степени перепутывания естественных или искусственных атомов.