Перепутывание в двухкубитной системе, индуцированное одномодовым тепловым шумом, при наличии атомной когерентности

Перепутанные состояния в настоящее время являются фундаментом квантовой информатики, квантовой криптографии, квантовых коммуникаций и квантовых вычислений [1; 2]. Перепутанными или запутанными называются состояния составных систем, которые нельзя разделить на отдельные, полностью самостоятельные и независимые части. Квантовая запутанность возникает в системе, состоящей из двух и более взаимодействующих подсистем (или взаимодействовавших ранее, а затем разделенных), и представляет собой суперпозицию макроскопически различимых состояний. В таких системах флуктуации отдельных частей взаимосвязаны, но не посредством обычных классических взаимодействий, ограниченных, например, скоростью света, а посредством нелокальных квантовых корреляций. В этом случае изменение одной части системы в тот же момент времени сказывается на остальных ее частях (даже если они разделены в пространстве, вплоть до бесконечно больших расстояний). Взаимодействие квантовых систем с окружением приводит к декоге-ренции, т. е. к разрушению суперпозиционного состояния в результате взаимодействия системы с окружающей средой. При этом уменьшается квантовая запутанность. В результате подсистемы начинают обосабливаться, отделяться друг от друга, вплоть до полной независимости (се- парабельности). Другой стороной процесса диссипации является возможность возрастания меры запутанности системы с окружением. Запутанность можно «концентрировать», увеличивать. Этот процесс называется рекогеренцией, или дистилляцией запутанности. Ряд работ в последнее время был посвящен исследованию возможности генерации перепутывания в атомных системах в резонаторах, индуцированного тепловым шумом. Идея о возможности возникновения перепутывания при взаимодействии атомов в резонаторах с тепловым полем принадлежит Питеру Найту с соавторами [3]. В целом интерес к атомам в резонаторах и ионам в оптических и магнитных ловушках обусловлен возможностью использования таких систем в качестве логических элементов квантовых компьютеров (кубитов). Для теоретического описания таких систем используется модель Джейнса – Каммингса и ее простейшие обобщения. Модель Джейнса – Каммингса и ее обобщения играют фундаментальную роль в квантовой оптике, поскольку позволяют описать все основные квантовые эффекты взаимодействия излучения с веществом. В частности, на примере двухатомной модели Джейнса – Каммингса можно исследовать особенности атомного перепутывания за счет взаимодействия атомов с различными бозонными полями. В последнее время интерес к одно- и двухатомным моделям особенно возрос в связи с их экспериментальной реализацией на атомах и ионах в резонаторах и ловушках, индивидуальных молекулах в органических кристаллах, искусственных атомах на квантовых точках, сверхпроводящих системах [2]. В работе [3] впервые было показано, что перепутывание всегда возникает при взаимодействии произвольной системы с большим числом степеней свободы в смешанном состоянии и одиночного кубита в чистом состоянии, и общие результаты проиллюстрированы на примере модели Джейнса – Каммингса одиночного атома в чистом состоянии, взаимодействующего с модой теплового поля в идеальном резонаторе. В своей следующей работе Питер Найт с соавторами [4] показали, что одномодовый тепловой шум может также индуцировать атом-атомное перепутывание в системе двух двухуровневых атомов в идеальном резонаторе. Перепутывание в двухатомной системе с вырожденным двухфотонным взаимодействием, индуцированное одномодовым тепловым шумом, было рассмотрено в работе [5].

Как хорошо известно, диполь-дипольное взаимодействие атомных систем является естественным механизмом возникновения атомного перепутывания. Наличие диполь-дипольного взаимодействия атомов, в частности, может привести к значительному увеличению степени перепутывания двух атомов, взаимодействующих с модой теплового поля в идеальном резонаторе как посредством однофотонных переходов [6], так и двухфотонных вырожденных [7] и невырожденных переходов [8–11]. Заметим, что атом-полевое перепутывание в таких моделях рассматривалось в наших работах [12; 13].

В работах [4–11] показаны двухатомные модели, в которых оба естественных или искусственных атома одновременно заперты в оптической ловушке. В то же время для практических применений в квантовой информатике часто необходимо перемещать атомы без потери квантовых корреляций между ними. Для реализации перепутывания атомов в таких условиях предложено большое число различных схем (см. ссылки в [14; 15]). В работах [14; 15] рассмотрена простая схема, в которой только один атом пойман в оптическую ловушку, а другой может перемещаться вне резонатора. При этом взаимодействие между атомами реализовано не за счет взаимодействия с общим полем, а благодаря прямому диполь-дипольному взаимодействию. При этом в качестве начального состояния поля рассмотрено состояние с определенным числом фотонов.

Однако генерации такого состояния резонаторного поля представляет собой существенную проблему. Поэтому представляет значительный интерес исследовать динамику перепутывания между атомами в рамках модели, рассмотренной в [14; 15], для теплового начального состояния резонаторного поля. В работах [16–19] показано, что начальная атомная когерентность может привести к заметному увеличению степени перепутывания атомов, взаимодействующих с тепловым полем в идеальном резонаторе. В настоящей работе нами исследовано влияние начальной атомной когерентности на динамику перепутывания двух идентичных атомов, один из которых заперт в резонаторе и взаимодействует с модой теплового поля, а другой может находиться вне резонатора. Заметим, что рассматриваемая в настоящей работе модель может быть естественным образом реализована также на двух сверхпроводящих джозефсоновских кубитах, один из которых взаимодействует со сверхпроводящим LC -контуром (электронным резонатором).

1. Модель и ее точное решение

Рассмотрим два идентичных естественных или искусственных атома, один из которых резонансно взаимодействует с квантованным полем частоты ω в одномодовом резонаторе. Второй атом находится вне резонатора. В случае если искусственные атомы представляют собой джозефсоновские сверхпроводящие кубиты, роль резонатора будет играть сверхпроводящий контур, в котором реализуются колебания электронной плотности. Будем также полагать, что атомы находятся на расстоянии, сравнимом с длиной волны излучения на их рабочих переходах. В этом случае необходимо учитывать прямое диполь-дипольное взаимодействие атомов. В результате гамильтониан модели может быть записан в виде

H = (1 / 2) h to ( c Z + с 2 ) + Й ю a ⁺ a +

+ Й g (a+a + a+c-) + hJ (a+c- + G-G+), где (1/2)σiz – оператор инверсии в i-м кубите (i ^^X c + =1+)ii <4 и c- =l->ii <+l - операторы переходов между возбужденным | +>i и основным состоянием | ->i в i-м искусственном атоме, a+ и a – операторы рождения и уничтожения квантов поля резонатора (фотонов электромагнитного поля в случае реальных атомов и квантов колебаний электронной плотности в случае сверхпроводящих кубитов), g – константа взаимодействия кубитов и одномодового квантованного поля резонатора и J – константа прямого диполь-дипольного взаимодействия кубитов. Двухкубитная волновая функция может быть представлена в виде произведения I V1, V2) = I V1 II V2), где V1, V2 = +, -.

Выберем когерентные начальные состояния для кубитов вида

| ^ 1 (0) ) = cos 9 1 | +) + e ^Ф 1 sin 9 1 | —) ,

| ^ 2 (0) ) = cos 9 2 | +) + e ^ ² sin 9 2 I -) .

^{I Ф} in ⁾ = C in ⁽ X i 1 n ^{I —} , ^— , ^{n + 2 ) +}

⁺ X i 2 n ^{I +} , ^— , ^{n + 1 +} X i 3 n ^{I —} , ⁺ , ^{n + 1 +}

+ X i 4 n I + , + , n ) )   ( i = 1,2,3,4).

Здесь

C in =

^{+ I} X i 2 n 2 ^{+ I} X i 3 n 2

– нормировочные константы и

_ (—1 + a2 + n n )^1 n         _

X ¹¹ n = 2V2V1 + n V2 + n a ^; X ¹² n =

^{+ I} X i 4 n 2

^{1 + a} 2 ^{— x} n _;

2V1 + na ’

Здесь 9 1 и 9 2 — амплитуды поляризованных кубитов, Ф 1 и ф 2 — относительные фазы возбужденного и основного состояний кубита в когерентной суперпозиции. В результате начальную атомную матрицу плотности можно представить в виде

Р a (0) =I ^ 1 (0) ) I ^(0)Х ^ 1 (0) I (^(Q) I. (2) Будем полагать также, что резонаторное поле в начальный момент находится в одномодовом тепловом состоянии

X 13 n =

X 21 n =

X 23 n =

X 31 n =

-

-

•xj 3 + 2 n + a

—

V2 V1 + n

^x n .

;

X 14 n

=1;

Р F (0) = ^ P n I П )( П I .

n

Здесь коэффициенты теплового распределения Бозе – Эйнштейна равны

X 33 n =

(—1 + a2 + n n )^1 n

2V2 V1 + n V2 + n a ’

•xj 3 + 2 n + a

—

V2 V1 + n

^x n .

;

(—1 + a2 — n n )^2 n

2V2V1 + n л] 2 + n a

—

•J 3 + 2 n + a2 + x n

X 22 n =

X 24 n = 1;

1 + a ² — n _n . 2V1 + n a ’

_ 1 + a + n n _

X 32 n =            ;

2V1 + n a

₌ nⁿ p n   (1 + П ) n ^{+ 1},

X 41 n =

2 V1 + n

(1 — a2 + n n )^2 n

2V2 V1 + n V2 + n a ’

; X _{34 n} = 1;

_ 1 + a + n n .

X 42 n =            ;

2V1 + n a

где n – среднее число «фотонов» в тепловой резонаторной моде n = (exp[h® / квТ] - 1)-1, kB – постоянная Больцмана и T – равновесная температура резонатора.

Тогда начальную матрицу плотности всей системы, включающей два кубита и моду теплового поля, можно представить в виде

Р(0) = Рa(0)Рf(0) = Ypn I ^1(0)) x n                              (3)

x I ^ 2 (0) )(^ 1 <0) I (^ 2 (0) II n )( n I,

X 43 n =

____^2n____• У. . - 1

V2 Vim ’ X ^{44 n} 1.

где

^1 n = V3 + 2 n + a2 — x n,

^2 n = V3 + 2 n + a2 + x n ,

X _n = ^ 1 + a ² ( б + 4 n + a ² ) ,

П _n = V1 + (6 + 4 n ) a ²

+ a ⁴.

Прежде чем рассмотреть динамику системы для теплового состояния резонаторной моды, исследуем поведение модели в случае фоковско-го состояния поля. В этом случае в качестве базиса для записи временной волновой функции можно выбрать полный набор атом-полевых функций вида I - , - , n + 2 ) , I + , - , n + 1 ) , I - , + , n + 1 ) , I + , + , n ) . Найдем в указанном базисе собственные функции и собственные значения гамильтониана (1). Собственные функции можно представить в виде

Соответствующие собственные значения энергии есть

E 1 n / h = ( n + 1) ®+ V A n + ^B n /2,

E 2 n / h = ( n + 1) ® — V A n + B n /2,

E 3 n / h = ( n + 1) ®+ V A n — B n /2,

E 4 n / h = ( n + 1) ® — V A n — B n /2.

Здесь

A n = 4 n + 6 + 2 a ²,

Bn = 2^4( n + 1)a2 + (a2 + 1), где a = J / g .

Для полного описания динамики модели мы должны рассмотреть также собственные значения и собственные функции гамильтониана (1) в базисе | - , - ,1 〉 , | + , - , 0 〉 , | - , + , 0 〉 :

| ϕ 1 〉 =( α ²/ Ω )[| - , - ,1 〉- (1/ α )| - , + ,0 〉 ],

E ₁ = 0;

| ϕ 2 〉 =(1/ 2)[(1/ Ω )| - , - ,1 〉+

+ | + , - ,0 〉+ ( α / Ω ) | - , + , 0 〉 ],

E 2 / й = Q ;

| ϕ 3 〉 =(1/ 2)[ - (1/ Ω )| - , - ,1 〉+

+ | + , - ,0 〉- ( α / Ω ) | - , + , 0 〉 ],

E2 / Й = -Q, где Ω = 1 +α2 .

Наконец, гамильтониан (1) имеет еще одну собственную функцию

Предположим, что изучаемая система в начальный момент времени приготовлена в состоянии | + , + , n 〉 ( n ≥ 0), тогда в последующие моменты времени эволюция системы будет описываться волновой функцией вида

| Ψ ( t ) 〉 = Z _{11, n} | - , - , n + 2 〉+ Z _{21, n} | + , - , n + 1 〉+ + Z _{31, n} | - , + , n + 1 〉+ Z _{41, n} | + , + , n 〉 .

Здесь

7    -io iE1 nt/^П V V

Z 11, n = e        C 1 n Y 41 n X 11 n

- iE»3 /Й^

+ e ^{2 n}   C 2 n Y 42 n X 21 n +

- e

_- e

+

iE t /Й„  __

3n   C3nY43nX31n + iE4 ntf^n v V C4nY44nX41n,

7    = о i^E 1 nt ^{/ Й} С V V

Z 21, n = e       C 1 n Y 41 n X 12 n

+

+

+

- iE n„ t /Й^

e  ^{2 n}   C 2 n Y 42 n X 22 n +

_- e

- e

iE t /Й_,  ——   „

3n   C3nY43nX32n + iE4 nt/Й/~| v V

C 4 n Y 44 n X 42 n ,

7    =o i ^E 1 n t/^p V V

Z 31, n = e       C 1 n Y 41 n X 13 n

+

+

+

- iE₉„t /Й^

e  ^{2 n}   C 2 n Y 42 n X 23 n +

_- e

_- e

iE t /" Й^

3n   C3nY43nX33n + iE4 ntf^o у у C4nY44nX43n,

Z 13 =

+

Z 23 =

Z 33 =

7 =o i^E 1 nt ^{/ Й} С V V

Z 41, n = e       C 1 n Y 41 n X 14 n

- iE»3 / Й„

+ e ^{2 n}   C 2 n Y 42 n X 24 n +

+

+

+

-

+ e

-

iE t /Й^

3n   C3nY43nX34n + iE4 nt/Йг* у у

C 4 n Y 44 n X 44 n ,

*

где Y ijn = C jn X jin .

Аналогично, если рассматриваемая система в начальный момент времени находилась в состоянии | + , - , n + 1 〉 ( n ≥ 0), то в моменты времени t ее волновую функцию можно записать как

|Ψ(t)〉=Z12,n|-,-,n+2〉+Z22,n|+,-,n+1〉+ +Z32,n|-,+,n+1〉+Z42,n|+,+,n〉, где явный вид коэффициентов Zi2,n (i = 1,2,3,4) может быть записан в виде (5) при замене везде Y4jn на Y2jn. Если же начальное состояние полной системы есть | +, -, 0〉, то временная волновая функция запишется как |Ψ(t)〉 =Z12 |-,-,1〉+ +Z22 | +,-,0〉+Z32 | -, +, 0〉,

где

i

Z = - sin Ω t ,

12 Ω ,

Z ₂₂ = cos Ω t ,

Z = - ⁱ α sin Ω t .

32 Ω

Для начального состояния | - , + , n + 1 〉 ( n ≥ 0) временная волновая функция может быть представлена как

| Ψ ( t ) 〉 = Z _{13, n} | - , - , n + 2 〉+ Z _{23, n} | + , - , n + 1 〉+ + Z _{33, n} | - , + , n + 1 〉+ Z _{43, n} | + , + , n 〉 .

Здесь коэффициенты Z_{i 3, n} ( i = 1,2,3,4) имеют вид (5) при замене везде Y _{4 jn} на Y _{3 jn} .

Для начального состояния | - , + ,0 〉 динамика системы описывается волновой функцией

| Ψ ( t ) 〉 = Z 13 | - , - ,1 〉+

+ Z ₂₃

| + , - ,0 〉+ Z ₃₃ | - , + , 0 〉 ,

где

-α (cos Ω t - 1), Ω ²

iα

- sin Ω t , Ω

-     (1 +α ² cos Ω t ).

Ω ²

В случае когда в начальный момент полная система приготовлена в состоянии | - , - , n + 2 〉 ( n ≥ 0), временная волновая функции может быть представлена в виде

| ЧЧ t ) > = Z 14, n ^{1 — , — ,} n + 2 > + Z 24, n ¹ + ^{, — , П} + 1 > +Ю) ⁺ Z 34, п | ^{— , + , П +} 1 >⁺ Z 44, п | ^{+ , + , П} > .

Здесь коэффициенты Z ^ 4 _П ( i = 1,2, 3, 4) имеют вид (5) при замене везде Y 4j _n на Y 1 j _n .

Начальное состояние | —, —,1> эволюционирует так, что

| Т ( t ) > = Z 14 | — , — ,1 ) +

⁺ Z 24 | ^{+ , — ,} 0 >⁺ Z 34 | ^{— , + ,} 0 >

где

Z 13 = ~ ( а ² + cos Q t ),

i

Z_{9 ч} =--sin Q t ,

• ²³     Q ^,

• Z 33 = — Л (1 — cos Q t ).

33     Q 2

Наконец, для начального состояния | — , — , 0 > в последующие моменты времени имеем

| ^ ( t ) > = e

—

■^{йш t} | — , — ,0 ) .

Теперь мы можем вернуться к рассмотрению динамики системы для теплового состояния поля и когерентных состояний кубитов. Если начальное состояние системы выбрано в виде (2), то, используя полученные ранее соотношения (4)–(12), мы можем получить временную зависимость полной матрицы плотности от времени. Усредняя найденную матрицу плотности по полевым переменным, мы можем получить редуцированную атомную матрицу плотности двух кубитов в виде

	'Р 11	р 12	р 13	Р 14 ^
	Р 12	р 22	р 23	р 24
Р A ( t ) =	^				.                      (13)
	Р 13	1 р 23	р 33	р 34
	1 1р 14	1 р 24	1 р 34	р 44 7

Явный вид элементов редуцированной матрицы плотности не приведен в настоящей статье ввиду ее громоздкости.

Для определения степени атом-атомного перепутывания воспользуемся параметром Пере-са-Хородецких, который определим как б = —2^Ц—,

i где ц — - отрицательные собственные значения транспонированной по переменным одного кубита атомной матрицы плотности рA, которая для двухкубитной системы с атомной матрицей плотности (13) может быть представлена в виде

( Р11 р12 1 р13 1 р23 T Р A1( t) = 1 р12 р22 1 р14 1 р24 .                     (14) р13 Р14 р33 р34 чр23 р24 1 р34 Р44 > Отсутствие у частично транспонированной по переменным одного кубита атомной матрицы плотности (14) отрицательных собственных значений означает, что атомы в любой момент вре- мени остаются неперепутанными, в этом случае полагают б = 0. Для случая б > 0 атомы находятся в перепутанном состоянии. Для максимально перепутанного состояния б = 1.

• 2. Результаты

Нами проведено численное моделирование параметра перепутывания атомов для различных параметров модели. На рис. 1–3 показаны результаты численного моделирования временной зависимости критерия Переса-Хородецких (13) для различных значений параметров модели. На рис. 1 представлена динамика атом-атомного перепутывания для различных начальных когерентных и некогерентных состояний кубита в случае низких температур резонатора ( n =0,01). Параметр интенсивности дипольного взаимодействия а = 0,1. Из рисунка хорошо видно, что наличие начальной атомной когерентности приводит к значительному увеличению степени перепутывания кубитов. Еще одной интересной особенностью рассматриваемой модели является возникновение перепутывания для начального состояния, в котором оба кубита возбуждены. Для моделей, в которых оба кубита одновременно заперты в резонаторе и взаимодействуют с полем, такое начальное состояние не порождает перепутанности кубитов для любых типов разрешенных переходов [4–18]. С увеличением интенсивности диполь-дипольного взаимодействия максимальная степень атомного перепутывания существенно возрастает только для некогерентных начальных состояний поля. На рис. 2 показана временная зависимость параметра перепутывания (13) для модели с П = 0,01 и а = 1 в случае начального атомного состояния вида | + , —> . Сравнивая риc. 2 и рис. 1, a , можно отметить, что для начального атомного состояния | + , —> увеличение интенсивности диполь-дипольного взаимодействия на порядок приводит к увеличению максимальной степени атомного перепутывания на два порядка. Исследование зависи-

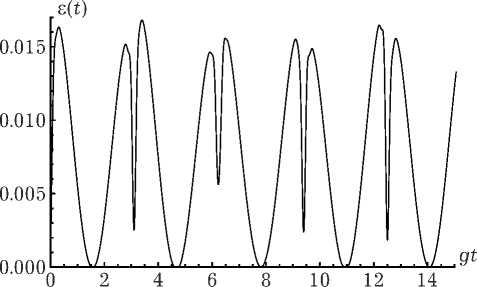
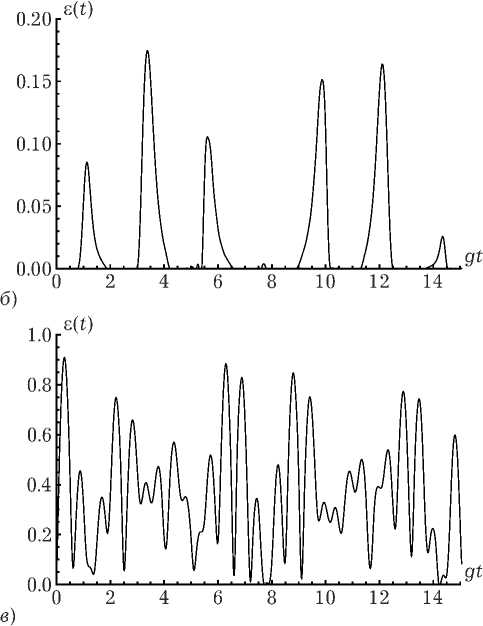
Рис. 1. Временная зависимость параметра перепутывания (13) для модели с n = 0.01 и а = 0,1. Начальные атомные состояния: | + , -> ( a ), | + , +> ( б ) и | Т (0) > A 1 = (1 / V2(| +> + | -> ), | т (0) > _Л = (1 / V2(| +>- 1 -> ) ( в )

мости параметра перепутывания от интенсивности теплового поля показывает, что увеличение среднего числа фотонов в резонаторной моде приводит к резкой деградации степени атомного перепутывания для когерентных начальных состояний кубитов (для средних чисел фотонов n >  3 перепутывание кубитов не возникает) и достаточно медленному уменьшению степени перепутывания для некогерентных состояний. На рис. 3 показана временная зависимость параметра перепутывания для модели с n = 10 и а = 1 и начального состояния кубитов | + , -> . Для моделей, в которых оба атома заперты в резонаторе, зависимость степени перепутывания от

£(t)

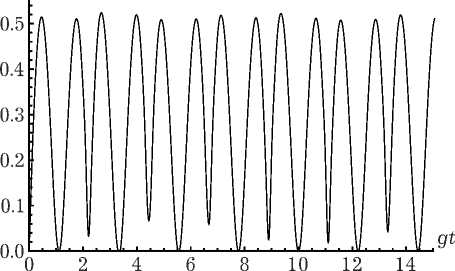
Рис. 2. Временная зависимость параметра перепутывания (13) для модели с n = 0.01 и а = 1. Начальное атомное состояние | + , ->

e(t)

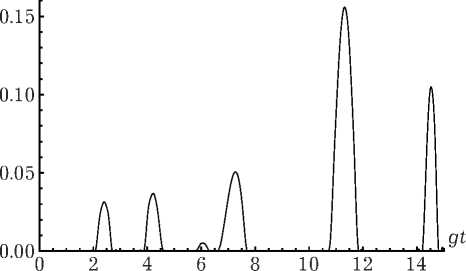
Рис. 3. Временная зависимость параметра перепутывания (13) для модели с n = 10 и а = 1. Начальное атомное состояние | +, -> интенсивности тепловой моды принципиально иная. В таких моделях перепутывание кубитов в случае интенсивного теплового поля сохраняется только для когерентных состояний атомов.

В результате мы можем заключить, что для рассматриваемой модели использование когерентных начальных атомных состояний позволяет добиться значительной степени атомного перепутывания в процессе эволюции рассматриваемой системы за счет диполь-дипольного взаимодействия в случае малых температур резонатора.

Заключение

Таким образом, в настоящей работе нами исследована простая двухкубитная схема, в которой только один из кубитов заперт в резонаторе и взаимодействует с тепловым полем, позволяющая получить перепутанные состояния двух кубитов, находящихся первоначально как в некогерентных, так и когерентных состояниях. Показано, что при наличии начальной атомной когерентности в модели возможна генерация высокой степени атом-атомного перепутыва- ния. Это означает, что атомная когерентность в такой модели может быть использована для эффективного контроля за степенью перепутанности кубитов.

При описании динамики перепутывания кубитов важен также учет диссипативных процессов, возникающих за счет взаимодействия кубитов с окружением. Такие взаимодействия приводят к распаду квантовых корреляций межу кубитами. Учет влияния окружения на динамику перепутывания кубитов, оценка времени декогеренции и других механизмов контроля в рамках рассмотренной в настоящей работе модели будет предметом нашей следующей работы. Метод вывода управляющих уравнений для редуцированной матрицы плотности моделей, аналогичных рассмотренной в настоящей работе, предложен ранее в наших работах [20–22].

Работа выполнена в рамках госзадания Министерства образования и науки Российской Федерации № 1394.