Перепутывание в многофотонной модели Тависа - Каммингса, индуцированное тепловым шумом
Автор: Башкиров Е.К.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 2 т.21, 2018 года.
Бесплатный доступ
В настоящей работе нами исследована динамика перепутывания двух естественных или искусственных двухуровневых атомов, взаимодействующих посредством многофотонных переходов с тепловым полем идеального микроволнового резонатора. На основе точного решения рассматриваемой модели найден параметра атом-атомного перепутывания для различных начальных сепарабельных и перепутанных состояний атомов. Показано, что взаимодействие атомов с тепловым полем резонатора посредством многофотонных переходов может индуцировать перепутывание атомов для всех состояний, кроме такого, в котором оба атома возбуждены. Установлено также, что максимальная степень перепутывания атомов возрастает с увеличением мультиплетности атомных переходов.
Естественные и искусственные атомы, тепловое поле, атом-атомное перепутывание, многофотонные переходы, управление перепутыванием
Короткий адрес: https://sciup.org/140256036
IDR: 140256036
Текст научной статьи Перепутывание в многофотонной модели Тависа - Каммингса, индуцированное тепловым шумом
Квантовые перепутанные состояния являются основным ресурсом квантовой информатики. Для приложений в физике квантовых вычислений нужны максимально перепутанные состояния с достаточно большим временем жизни [1]. В настоящее время предложены и частично реализованы различные схемы генерации и использования атомных перепутанных состояний. Атом-атомные перепутанные состояния наблюдались в ряде экспериментов с ионами и атомами в магнитных и оптических ловушках, сверхпроводящими джозефсоновскими кубитами, примесными спинами, квантовыми точками и др. [2; 3]. Однако в реальных условиях квантовые системы всегда взаимодействуют с окружением. Такое взаимодействие обычно приводит к декогерентности, так что исследуемая система эволюционирует в смешанное состояние, которое оказывается непригодным для целей квантовых вычислений. Поэтому с практической точки зрения основная задача при получении и использовании атомных перепутанных состояний заключается в том, чтобы предотвратить, минимизировать или использовать влияние шума. Было высказано большое количество предложений по защите, минимизированию или использованию влияния окружения для создания и сохранения, максимально перепутанных состояний, напри- мер стратегия кольцевого контроля, коррекция квантовых ошибок, использование избыточного кодирования и др. Однако указанные способы успешно решают проблему только при малой скорости генерации ошибок в исследуемой системе. Более экономичный подход состоит в использовании так называемых свободных от де-когеренции пространств, которые полностью нечувствительны к специфическим типам шумов. Такой подход, однако, также требует использования дополнительных источников и эффективен только для определенного окружения.
Недавно в целом ряде работ была высказана идея о том, в некоторых случаях диссипация и шум могут, напротив, являться источником перепутывания. Впервые такая идея была предложена в работе [4]. В ней авторы показали, что за счет диссипации два атома в оптическом резонаторе могут перейти в максимально перепутанное состояние, в то время как в отсутствии диссипации редуцированное состояние двухатомной системы представляет собой несепарабельную смесь атомных состояний. Возможность генерация перепутанных состояний в системе двух и более атомов в резонаторе за счет различных механизмов диссипации рассматривалась позднее в большом количестве работ. В работе [5] рассмотрено возникновение атомного перепутывания в системе двух двухуровневых атомов в резонаторе при наличии диссипации за счет утечки фотонов и спонтанного излучения, а также при наличии белого шума. Позднее влияние вакуумного шума, фазового шума, теплового шума, различных типов классического шума и комбинации различных видов шумов на возникновении и исчезновение перепутывания атомов в резонаторе рассматривалось в большом числе работ (см. ссылки в [6–8]).
Ряд работ в последнее время был посвящен исследованию возможности генерации перепутывания в атомных системах в резонаторах, индуцированного тепловым шумом. Идея о возможности возникновения перепутывания при взаимодействии атомов в резонаторах с тепловым полем принадлежит Питеру Найту с соавторами [9]. В целом интерес к атомам в резонаторах и ионам в оптических и магнитных ловушках обусловлен возможностью использования таких систем в качестве логических элементов квантовых компьютеров (кубитов). Для теоретического описания таких систем используется модель Джейнса – Каммингса и ее простейшие обобщения. Модель Джейнса – Каммингса и ее простейшие обобщения играют фундаментальную роль в квантовой оптике, поскольку позволяет описать все основные квантовые эффекты взаимодействия излучения с веществом. В частности на примере многоатомной модели Джейнса – Каммингса, которую также часто называют моделью Тависа – Каммингса, можно исследовать особенности атомного перепутывания за счет взаимодействия атомов с различными бозонными полями. В последнее время интерес к одно и многоатомным моделям в резонаторе особенно возрос в связи с их экспериментальной реализацией на атомах и ионах в резонаторах и ловушках, индивидуальных молекулах в органических кристаллах, искусственных атомах на квантовых точках, сверхпроводящих системах [2; 3]. В работе [9] впервые было показано, что перепутывание всегда возникает при взаимодействии произвольной системы с большим числом степеней свободы в смешанном состоянии и одиночного атома в чистом состоянии, и общие результаты проиллюстрированы на примере модели Джейнса – Каммингса одиночного атома в чистом состоянии, взаимодействующего с модой теплового поля идеального резонатора. В своей следующей работе Питер Найт с соавторами [10] показали, что одномодовый тепловой шум может также индуцировать атом-атомное перепу- тывание в системе двух двухуровневых атомов в идеальном резонаторе. Перепутывание в двухатомной системе с вырожденным двухфотонным взаимодействием, индуцированное одномодовым тепловым шумом, было рассмотрено в работе [11], а влияние двухмодового теплового шума на перепутывание двух двухуровневых атомов с невырожденными переходами и переходами рамановского типа – в работе [12]. При этом было показано, что при двухфотонном взаимодействии степень перепутывания атомных состояний может превосходить соответствующую величину для однофотонного взаимодействия. Представляет интерес исследовать возможность возникновения перепутывания двух атомов за счет многофотонного взаимодействия с тепловым полем идеального резонатора. Поэтому в настоящей работе нами найдено точное решение для двухатомной многофотонной модели Тави-са – Каммингса в случае теплового поля резонатора и с его помощью исследована динамика перепутывания атомов для их различных начальных состояний и интенсивностей теплового поля.
1. Модель и базовые уравнения
Рассмотрим систему двух естественных или искусственных атомов (сверхпроводящих атомов, примесных спинов, ионов в ловушках, квантовых точек) резонансно взаимодействующих с модой микроволнового теплового квантового электромагнитного поля идеального копла-нарного резонатора посредством вырожденных m -фотонных переходов. Гамильтониан такой системы в представлении взаимодействия может быть записан в виде
H = Й g ^ ( о + a m + о - (a + ) m ), (1) i =1
где a ( a + ) — оператор уничтожения (рождения) фотонов моды поля; о+ ( о - ) — повышающий (понижающий) операторы для i -го атома ( i = 1, 2); g – эффективная константа вырожденного m -фотонного атом-полевого взаимодействия и m – мультиплетность перехода. При записи гамильтониана (1) мы предполагаем наличие m -фотонного резонанса to o = to m , где to o — частота перехода в двухуровневом атоме и to — частота резонаторной моды.
Предположим, что в начальный момент времени атомы находятся в произвольной суперпозиции сепарабельных двухатомных состояний вида
| W)) A = а | + , -) +
+ P | + , -) + Y | + , -) + 8 | + , -) ,
+ X 3 n ( t ) | - , + , n + m ) +
+ X 4 n ( t ) | - , - , n + 2 m ) ) ,
где | +) и | -) — возбужденное и основное состояние двухуровневого атома и
| а 2 + | 8 2 + | y 2 + | 8 2 = 1.
где коэффициенты имеют вид
X 1 n ( t ) =
-
e
4 Q n ( - 1)3/2
- V2 i Q n t
x
При определенном выборе коэффициентов а , 8 , Y , 8 (2) может описывать как сепарабельные состояния атомов вида
x J 4 b n i Q nei Q nt а + 2 a2ni Q n f 1
2V2 i Q t ) + e n | а -
| + , +) , | + , -) , | -, +) , | -, -) (3)
-
1 2V2 i Q„ t V, .
- 1 + e n l ( P + y ) +
так и перепутанные состояния атомов, в частности белловское состояние вида
| W) ) a = a | + , -) + b | - , +) , (4)
где | а 2 + | b 2 = 1 Легко также заметить, что формально сепарабельное состояние | + , -) является частным случаем состояния (4) при условии b = 0. Для чистого состояния атомов (2) начальная атомная матрица плотности имеет вид
Р a (0) = | Y (0) ) aa <^ (0) | .
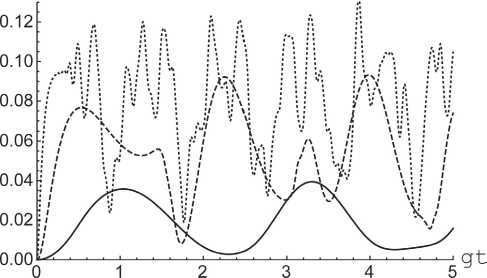
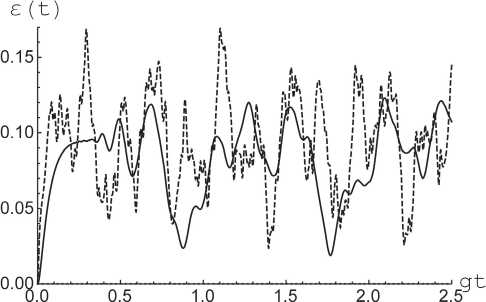
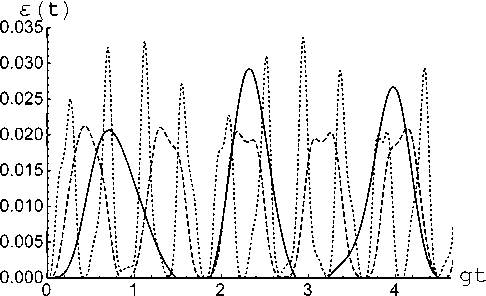
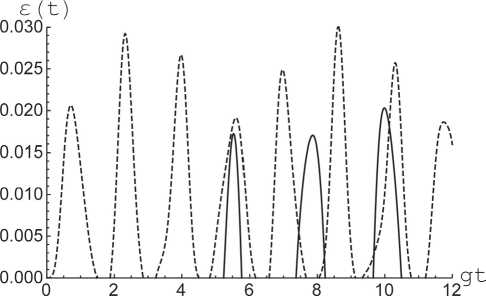
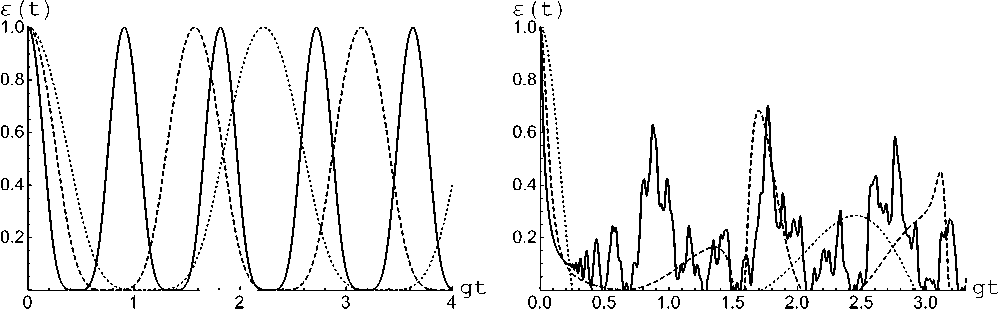
Предположим также, что поле находится в тепловом одномодовом состоянии, описываемом матрицей плотности рF(0) = ^Pn|n) n где вероятности + + anbn 2 iQ n - X 2 n (t) = 1 2V2i Q„ t Yo x -1 + e n l (P + y) + V2i Q„ t )2 n 2 (Qn) + + (Qn) (P + y)cos(V2q nt) + + i V2iQ n (an а + bn 8) i sin(V2Q nt)), X 3 n (t) = 2 (Q2n) (-(Qn)(P - y) + + (Q2n) (P + y)cos(V2q nt) + + i V2iQ n (an а + bn 8) i sin(V2Q nt)), pn = Здесь (1 + n)n+1 . n – среднее число тепловых фотонов в моде резонатора n = (exp[Ato / kBT] - 1]-1, kB – постоянная Больцмана и T – равновесная температура резонатора. Прежде чем исследовать взаимодействие атомов с тепловым полем, рассмотрим их взаимодействие с полем резонатора в фоковском состоянии. Обозначим через n номер возбуждения рассматриваемой системы «два атома+мода поля». Тогда для значения номера возбуждения n > 0 эволюция системы происходит в гильбертовом пространстве с базисом | -, -, n + 2m), | +, -, n + m), | -, +, n + m), | +, +, n). Для начального состояния атомов (2) и поля в фоковском состоянии | n) временную волновую функцию всей системы можно представить в виде X 4 n (t) = - e 4Qn (-1)3/2 - V2i Q„ t ! n X ( x 2anbniQn . V2i Qnt )2 -1 + e n l а + \ + an . 2V2i Q„ t) -1 + e n lx x (p + y)4iQne"^iQnt8| + + bn + 2 iQ n Здесь an bn Q n , 2V2i Q„tVn x -1 + e n l (P + y) + 2V2i Q„ t n (n + m)! n! , (n + 2 m)! (n + m)! ’ n 2 n. | Yn (t))= X1 n (t) | +, +, n) + +X2n(t) | +, -, n +m) + Если атомы приготовлены в начальный момент времени в суперпозиции состояний | ^(0))a = a|+, -) + b|-, +), а поле – в одном из фоковских состояний вида | k) (k = 0,..., m — 1), временная волновая функция системы примет вид | Ф k (t)) = Y1,k (t) | +, —, k) + +Y2,k(t) I —, +, k) + Y3,k(t) I —, —, k + mX Y10(t) Y20(t) Y30(t) 12( 21( —i Y11( t) = 2( a — b + + a cos[д/2(m + 1)!t] + b cos[^2(m + 1)!t], Y21(t) = 2(—a+b+ + a cos[^2(m + 1)!t] + b cos[^2(m + 1)!t], —i Y31( t) = Vl^ a + b) sin[V2m + 1)!t ], Y31( t) = cos[V2( m + 1)!t ], Z1, m—1( t) = sin[V2(2 m — 1)!/( m — 1)!t ])], Z2, m—1( t) = sin[V2(2 m —1)!/( m — 1)!t ])], Z3, m—1( t) = cos[72(2m^1)!7CmT1)!t ]. Наконец, для атомов, приготовленных в начальный момент времени в состоянии, Y(0))a = | —, —), а поля — в одном из фоковских состояний | k) (k = 0, ..., m — 1), временная волновая функция есть | Г k (t )) = |—, —, k). Используя формулы (6)–(9) мы можем найти временную матрицу плотности полной системы для теплового начального состояния поля как р(t) = U(t)pF (0) ®pA (0)U+(t) = = ^ pj^ n (t)X^ n (t) I + ^. Y m—1( t) = = (a — b + a cos[^/2(2m — 1)! / (m — 1)!t] + + b cos[-72(2 m — 1)!/ (m — 1)!t ], Y2 m—1( t) = = (—a + b + a cos[-j2(2m — 1)! / (m — 1)!t] + + b cos[^2(2 m — 1)!/ (m — 1)!t ], Y3,m 1( t) = = 1 (2c cos[V2(2m — 1)!/(m — 1)!t] — — iV2a sin[A/2(2m — 1)! / (m — 1)!t], Если атомы приготовлены в начальный момент времени в состоянии | ^(0))a = | —, —), а поле - в 2. Вычисление параметра перепутывания Для исследования атомного перепутывания в рассматриваемой двухатомной модели будем, как обычно, использовать параметр Переса – Хородецких (см., например, [12]). Для его вычисления необходимо найти редуцированную матрицу плотности атомной подсистемы, которую можно получить, усредняя матрицу плотности полной системы (10) по полевым переменным pa (t) = TrFU(t)pf (0) ® pa (0)U+(t). Для рассматриваемых начальных состояний системы редуцированная атомная матрица плот- одном из фоковских состояний | k + m) (k = 0, m — 1), временная волновая функция есть | 5k(t)) = Z1, k(t) | +, —, k) + +Z2,k(t) | —, +, k) +Z3,k(t) | —, —, k + mX Z10(t) Z20(t) i 2 i ..., ности имеет вид ' U (t) 0 0 0 ^ 0 V (t) H (t) 0 Pa (t) = * . (11) 0 H (t) W (t) 0 v0 0 0 R (t) ? Для начального атомного состояния | ^(0)) a = | +, +) матричные элементы (11) имеют вид Z30(t) Z11(t) = cos[V2 m !t ], —i = —;= sm[J2( m + 1)!t ], —i . _ it-.-------— _ Z21( t) = -y^sin[V2( m + 1)! t ]’ да U(t) = ^Pn I X1,n(t) I2, n=0 да V(t) =2Pn|X2,n(t) I2, n=0 да W(t) = ^Pn | X3,n (t) |2, n=0 to R(t) = 2Pn | X4,n (t) 2, n=0 to H (t) = 2PnX 2, n (t) X *, n (t). n=0 В случае атомного состояния | Y(0)) a = a | +, -) + + b | -, +) элементы есть to U (t) = 2 Pn|X1, n - m (t )2, n=m to V(t) =2 Pn | X2,n-m (t) 2 + 2 Pk | Y1,k (t) 2, n=mk to W(t) = 2 Pn | X3,n-m (t) 2 + 2Pk | Y2,k (t) 2, n=mk to R(t) =2 Pn | X4,n-m (t) 2 +2Pk | Y3,k (t) 2, n=mk to E* PnX2,n-m(t)X3,m-n(t) + n=m m -1 E* PkY1, k(t ) Y2, k(t )• k=0 Наконец, для начального состояния | Y(0))a = = | -, -) матричные элементы принимают вид to U(t) =2 Pn | X1,n-2m (t) 2, n=2m to V(t) = 2 Pn|X2,n-m (t)2 + n=2m m -1 + 2 Pm - k\Z1, k (t )2, k=0 to W(t) = 2 Pn|X3, n-2m (t)2 + n=2m m -1 + 2 Pm - k । Z2, k (t) 2, k=0 to R(t) =2 Pn | X4,n-2m (t) 2 + n=2m m -1 + 2 Pm - k|Y3, k (t )2 + P0, k=0 to 2* PnX2,n-2m(t)X3,m-n(t) + n=2m m -1 + 2 Pm -kZ1,k (t)Z2,k (t)• k=0 Параметр Переса – Хородецких (отрицательность) можно определить как s(t) = -2 2p-, i где ^j — отрицательные собственные значения частично транспонированной по переменным одного атома матрица плотности. Необходимым и достаточным условием сепарабельности (перепутанности состояний) атомов является неотрицательность параметра Переса – Хородецких. Для максимально перепутанного состояния атомов б = 1. Для сепарабельного состояния б = 0. Для (11) частично транспонированная по переменным одного атома редуцированная матри- ца плотности имеет вид H (t) ^ U (t) 0 0 T Р A1( t) = 0 V(t) 0 0 . (12) 0 0 W(t) 0 1H (t) 0 0 R (t) ? Матрица (12) имеет всего одно собственное значение , которое может быть отрицательным. В результате параметр перепутывания рассматриваемой модели может быть представлен в виде б(t) = V(U(t) - R(t))2+ 4 | H(t) |2- U(t) - R(t). (13) Результаты численных расчетов отрицательности (13) для рассматриваемой модели в случае различных начальных состояний атомов и интенсивностей теплового шума представлены на рис. 1–5. На рис. 1 и 2 представлена зависимость параметра перепутывания от приведенного времени gt для двухатомной многофотонной модели Тависа – Каммингса с различными значениями мультиплетности m в случае сепарабельного начального состояния атомов | +, -)• Из рисунков хорошо видно, что в случае вакуумного состояния поля максимальная степень перепутывания атомов не зависит от мультиплетности разрешенных переходов в атоме. Для теплового состояния поля резонатора ситуация принципиально иная. В указанном случае максимальная степень перепутывания атомов растет с увеличением m. Таким образом, использование атомов с многофотонными переходами позволяет увеличить степень их перепутывания. На рис. 3 и 4 представлена зависимость параметра перепутывания от приведенного времени gt для сепарабельного начального состояния атомов | -, -)• Из рисунков £ (t) а) Рис. 1. Временная зависимость отрицательности для сепарабельного начального состояния атомов | +, - и различных значений мультиплетности m = 1 (сплошная линия), m = 2 (штриховая линия) и m = 3 (точечная линия). Среднее число фотонов в моде n = 0 (а) и n = 3 (б) б) Рис. 2. Временная зависимость отрицательности для сепарабельного начального состояния атомов | +, -) и различных значений мультиплетности m = 3 (сплошная линия) и m = 4 (штриховая линия). Среднее число фотонов в моде n = 3 Рис. 4. Временная зависимость отрицательности для сепарабельного начального состояния атомов | -, -) и различных значений мультиплетности m = 2 (сплошная линия), m = 3 (штриховая линия) и m = 4 (точечная линия). Среднее число фотонов в моде n = 0.3 Рис. 3. Временная зависимость отрицательности для сепарабельного начального состояния атомов | -, -) и различных значений мультиплетности m = 1 (сплошная линия) и m = 2 (штриховая линия). Среднее число фотонов в моде n = 0.3 видно, что для выбранного начального состояния зависимость максимальной степени перепутывания от мультиплетности m носит более сложный характер. Так для двухфотонной модели максимальное перепутывание атомов в случае двухфотонной модели больше, чем для однофотонной, а для трехфотонной модели перепутывание меньше, чем для двухфотонной. В то время как для четырехфотонной модели степень перепутывания выше, чем для трехфотонной и т. д. Для состояния атомов | +, +) перепутывание не возникает для любых значений мультиплет-ности атомных переходов. На рис. 5 показана временная зависимость отрицательности для многофотонной модели в случае перепутанного белловского начального состояния атомов вида 1 / V2(| +, -)+ | -, +)). Хорошо видно, что для вакуумного поля максимальная степень перепутывания не зависит от мульти-плетности, а для теплового поля максимальная степень перепутывания уменьшается со временем тем быстрее, чем больше мультиплетность m перехода. Заключение Таким образом, мы показали возможность возникновения перепутывания в системе двух двухуровневых атомов за счет взаимодействия с тепловым одномодовым полем для различных сепарабельных и перепутанных состояний ато- а) б) Рис. 5. Временная зависимость отрицательности для перепутанного начального состояния атомов 1 / V2(| +, -)+ | -, +)) и различных значений мультиплетности m = 1 (сплошная линия), m = 2 (штриховая линия) и m = 3 (точечная линия). Среднее число фотонов в моде n = 0 (a) и n = 3 (б) мов, за исключением случая, когда оба атома возбуждены в начальный момент времени. Было также показано, что для сепарабельного состояния | +, -) увеличение мультиплетности перехода в атоме приводит к существенному увеличению степени атомного перепутывания, что может быть использовано для контроля за степенью перепутывания атомов в резонаторе.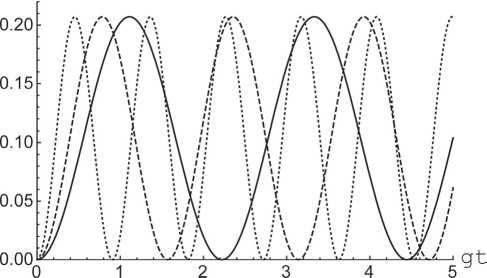
Список литературы Перепутывание в многофотонной модели Тависа - Каммингса, индуцированное тепловым шумом
- Buluta I., Ashhab S., Nori F. Neutral and artificial atoms for quantum computation // Rep. Prog. Phys. 2011. Vol. 74. P. 104401p.
- Hybrid quantum circuits: superconducting circuits interacting with other quantum systems / Z.-L. Xiang [et al.] // Rev. Mod. Phys. 2013. Vol. 85. P. 623-653.
- Georgescu I.M., Ashhab S., Nori F. Quantum simulation // Rev. Mod. Phys. 2014. Vol. 88. P. 153-185.
- Cavity-loss-induced generation of entangled atoms / M.B. Plenio [et al.] // Phys. Rev. 1999. Vol. A59. №. 3. P. 2468-2475.
- Tanas R., Ficek Z. Entangling two atoms via spontaneous emission // J. Opt. 2004. Vol. B6. P. S90-S97.
- Yi X.X., Yu C.S, Song H.S. Noise-assisted preparation of entangled atoms // Phys. Rev. 2003. Vol. 68. P. 052304.
- Stationary state entanglement of two atoms inside an optical cavity under noise / C. Ozel [et al.] // Int. J. Theor. Phys. 2008. Vol. 47. P. 3101-3107.
- Yu T., Eberly J.H. Entaglement evolution in a non-Markovian environment // Opt. Commun. 2010. Vol. 283. P. 676-680.
- Subsystem purity as an enforcer of entanglement / S. Bose [et al.] // Phys. Rev. Lett. 2001. Vol. 87. P. 050401.
- Entanglement induced by a single-mode heat environment / M.S. Kim [et al.] // Phys. Rev. 2002. Vol. A65. P. 040101.
- Zhou L., Song H.S. Entanglement induced by a single-mode thermal field and criteria for entanglement // J. Opt. 2002. Vol. B4. P. 425-429.
- Bashkirov E.K. Entanglement induced by the two-mode thermal noise // Laser Physics Letters. 2006. Vol. 3. № 3. P. 145-150.


