Перестановка слагаемых в бесконечных суммах

При перемене мест слагаемых в бесконечных суммах итоговая сумма не меняется.

Правило

Со школьной скамьи всем известно правило, появившееся ещё в древности: от перестановки мест слагаемых сумма не меняется. По умолчанию подразумевается, что количество слагаемых и их величина остаются неизменными. Если мы изменим количество слагаемых или изменим величину хотя бы одного из них, о перестановке слагаемых уже не может быть речи. В этом случае мы перешли от одной суммы к другой и эти две суммы никак между собой не связаны.

Пример перестановки

В статье «Что не так с перестановкой слагаемых?» [1, стр.12], приводится пример бесконечной суммы, якобы доказывающий, что итоговая сумма зависит от порядка сложения. Рассмотрим этот пример с более тщательным соблюдением правил записи математических выражений.

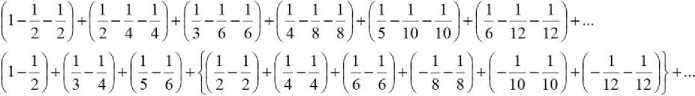
, 1    1   1    1    I Г 1    1   11

1  ----F — I-----1 1-----?

2  3  4  5  б[ 4  5  6J

,11111 fill!

1--4----^-----F...1------

2 3 4 5 6    I 4 5 6j

В первой строке представлена исходная бесконечная сумма, состоящая из шести скобок – по три слагаемых в каждой скобке. Общее количество слагаемых равно 18, итоговая сумма выражения равна нулю. Всё математическое выражение можно разделить на две группы: видимая часть выражения, представленная 18-тью слагаемыми и невидимая часть выражения, состоящая из бесконечного количества скобок, по три слагаемых в каждой скобке. Эти две части разделяет троеточие бесконечности. Обе части равняются нулю.

Во второй строке представлены те же 18 слагаемых после перестановки. Первые три пары слагаемых будут в дальнейшем представлены в видимой части выражения . Фигурными скобками выделена компенсирующая группа слагаемых .

В третьей строке шесть слагаемых видимой части остаются без изменений. Компенсирующая группа , после упрощения выражения, представлена тремя слагаемыми. Итоговый результат после перестановки слагаемых не изменился и по-прежнему равен нулю.

Четвертая строка не имеет к математике отношения. Это обычный фокус иллюзиониста, спрятавшего компенсирующую группу слагаемых в рукав бесконечности ( невидимая часть выражения ). Цель этого трюка – убедить доверчивых зрителей в «правдивости» ложного утверждения об изменении итоговой суммы после перестановки слагаемых.

Можно привести и более грубый пример перестановки слагаемых в данном выражении. Если в видимой части выражения показать слагаемые только с одним знаком, у зрителей неизбежно возникнет вопрос, куда подевались слагаемые с противоположными знаками, а это явно затруднит демонстрацию фокуса.

Перестановку слагаемых в бесконечных суммах наглядно демонстрирует принцип сообщающихся сосудов. Первый сосуд – это видимая часть выражения . Второй сосуд – это невидимая часть выражения , включающая компенсирующую группу слагаемых . Троеточие бесконечности – это соединительный патрубок между сосудами. Итоговая сумма выражения – это общий объем жидкости в двух сосудах. Поскольку в нашем математическом примере итоговая сумма равна нулю, то применительно к сообщающимся сосудам, мы рассматриваем первоначальный общий уровень жидкости в сосудах, как ноль относительной системы координат. Изменение количества или величины слагаемых в видимой части

Доклады независимых авторов 2022 выпуск 54 выражения будет приводить к изменению количества или величины слагаемых в компенсирующей группе .

Если последнее выражение рассматривать без невидимой компенсирующей группы слагаемых , тогда это будет не результат перестановки слагаемых, а совсем другая бесконечная сумма, содержащая только часть слагаемых из первоначального выражения и никак с ним не связанная. Доказательством этого факта является разная итоговая сумма двух выражений.