Performance Analysis of Rayleigh and Rician Fading Channel Models using Matlab Simulation

Published Online August 2013 in MECS

An explosive development of the wireless technology has opened several new paths for its implementation, however some unavoidable circumstances attenuate the signal energy and make barriers to achieving the optimum results from the system [1]. The radio link between the transmitter and receiver varies from simple line-of-sight to one that is severely obstructed by the buildings, mountains etc, and hence suffers from severe multipath fading [1-7]. However, the mobile channels are very different from the stationary as well as predictable wired channels, because of their randomness. There are several factors which determine the behavior of a channel such as terrain features between the transmitter and receiver, the speed of transmitter and receiver, weather conditions etc. Over the years, several studies and measurements have been undertaken in different locations for such channels and various models have been proposed for both the indoor and outdoor environments [3, 4]. The instantaneous signal strength at the receiver can be predicted using the traditional large-scale and small-scale models, wherein the large-scale models predict the average received signal strength depending on the transmitter-receiver distance and the small-scale channel models represent local variations of the average signal strengths [8-13]. The lognormal model, in which the measured signal levels have a normal distribution about the mean received signal, are suitable for emulating the large scale fading effects for the mobile channels models. The normal deviation about the mean captures the random shadowing effects that occur because of the variation in the clutter surrounding a moving vehicle, though the mean signal strength at the vehicular receiver remains the same. The frameworks for modeling and simulating the satellite channel along with the time variations have been extensively reported in the literature [14-16]. It is widely accepted that, while the lognormal-Rayleigh model accurately depicts the shadowed channel, a Rician channel model is more appropriate for the unshadowed channel [9-21].

However, the error performance modelling of the wireless channels is inherently depends upon the radio propagation modes such as line-of-sight, reflections, diffraction and scattering caused by an object with dimensions on the order of wavelength [1]. One of the most disturbing aspects in the wireless communication is fading, which is present when there are several multipath components and these components arrive at the receiver at slightly different times. If there is movement in the system then there is also phase difference between the received components, which leads to shift in the frequency. However, in the multipath propagation, the movement of the transmitter/receiver or both and bandwidth of the signal are the factors that influence the fading and multipath delay nature of the channel, which is quantified by the delay spread and coherence bandwidth [11]. The timevarying nature of the channel caused by the movement is quantified by Doppler spread and Coherence time [16-21]. In the high mobility scenario, the relative motion between the transmitters and receivers results rapid time variation and significant Doppler shift. Accumulating dynamically changed multipath effects and noise, a significant fluctuation in the received signal strength is observed in the channel. However, the fading is often modelled in the literature with the Rayleigh fading model. The Rayleigh fading model has not been challenged until very recently when researchers started to focus on the throughput problem at vehicular speeds. The Rayleigh fading model works on the assumption that the resultant fading arises from a large number of uncorrelated partial waves with identically distributed amplitudes and uniformly distributed random phases [19-21]. This assumption is highly optimistic in the mobile communication environment at high vehicular speeds. However, more realistic assumption is to have many partial waves with amplitudes which follow the distributions that are not identical, yet are partially correlated [19, 21]. Doppler spread is another effect of mobility, which changes the signal frequency over time. When the coherence time becomes small relative to the delay constraint of the channel, it results bit error rate at the receiver, which depends on the fading severity of the channel. According to the fading severity, the channel is divided into three categories, and different distribution models are used to estimate that channel according to the type of fading, which is described in the following section.

In this paper, we have developed an algorithm for the Rayleigh and Rician fading channel in a vehicular environment. The remainder of the paper is organized as follows. Section II discusses the performance of the Rayleigh fading model and proposes algorithm. Section III explores the Rician fading channel model and developed an algorithm for it. Finally, Section IV concludes the work.

• II.    Performance Analysis of Rayleigh Fading Channel Model

In a heavily built-up urban or where there is non-line-of-sight communication between the transmitter and receiver, the objects in the environment attenuate, reflect, refract, and diffract the signal before it arrives at the receiver. This propagation environment is known as Rayleigh fading, and the Rayleigh distribution model is a specialized stochastic fading model for this type of fading environment. The channel fading depends on moving speed of the receiver and/or transmitter. The amplitude gain of this fading channel is characterized by the Rayleigh distribution [19]. However, the constructive and destructive nature of the multipath components in the flat fading channels can be approximated by the Rayleigh distribution if there is no line-of-sight, which means when there is no direct path between the transmitter and receiver. The mobile antenna, instead of receiving the signal over one line-of-sight path, receives a number of reflected and scattered waves because of the varying path lengths, the phases are random, and consequently, the instantaneous received power becomes a random variable. In the case of an un-modulated carrier, the transmitted signal at frequency ωc reaches the receiver via a number of paths, the ith path having an amplitude ai, and a phase ф . If we assume that there is no direct path or line-of sight component, the received signal s (t) can be expressed as [9]:

N

• ⁵ ( t ) = ^ a i ^c osU)J + ^ф i )                    (1)

i = 1

where N is the number of paths. The phase ф i depends on the varying path lengths and change by 2 when the path length changes by a wavelength. When there is relative motion between the transmitter and the receiver, the Equation (1) can be modified to include the effects of the motion induced frequency and phase shifts.

Let the i^th reflected wave with amplitude a i and phase ф arrive at the receiver from an angle ^ i relative to the direction of motion of the antenna. The Doppler shift of this wave is given by:

^ v

• ^ di =---- cos ^ i                               (2)

c where v is the velocity of the mobile object, c is the speed of light, and the ^i’s are uniformly distributed over [0, 2π]. The received signal s (t) can now be written as:

• ^{5 ( t )} = 2₁ у a i cos ^ c t ⁺ ® di t ^{+ Ф} i )             ⁽³⁾

By expressing the signal in phase and Quadrate form, Equation (3) can be written as:

• 5 ( t ) = I ( t ) cosi a c, t + Q ( t ) sin ro _c t                  (4)

where the in-phase and Quadrate components are given as:

I(t) = ^у ai co^dit + Фi )

Q(t)=Z,=lai sin (^dit + фi )

and the envelope R is given by:

R = 7[I (t )]2 + [Q (t )]2

When N is large, the in-phase and Quadrate components will be Gaussian nature. The probability density function (PDF) of the received signal envelope, f (r), can be shown to be Rayleigh given by [12,21]:

r ²

f ( r ) = r4^e 2° 2                            (8)

<7

where 7 ² is the time-average power of the received signal before the envelope detection.

• 2.1    Proposed Algorithm for Rayleigh Channel

In this section, we have proposed the algorithm for Rayleigh fading channel. The proposed algorithm completes its functioning in four different steps, where step-1 declares about the various used variables in the proposed algorithm and step-2 is associated with the sending of data through Rayleigh channel. In step-3, an envelope is designed for received Rayleigh signal using QAM amplitude demodulation on the received signals. Finally, the step-4 computes the outage probability using the theoretical and simulated methods.

Algorithm: Rayleigh Fading Channel

STEP 1: Variable Declaration

• V: Input Velocity in miles/sec.

P: Input number of paths

T: Time array

Λ: Carrier frequency

η: Sampling frequency

ω: Radian frequency

δ: Data frequency

τ: Sampling periods

θ: Received Rayleigh signals

ρ: Threshold power

δ: Threshold outage

σ: Weibull distributiob function

• E: Rayleigh envelop

STEP 2: Sending of Data through Rayleigh Channel

• 0 ^ Make an array of zeros [T]

FOR I := 1 : P

Calculates the value of δ;

3 ^ 2*pi*V*Л*cos(for uniform random distribution);

Find the value of σ;

9 ^ 9 + a*cos(Л+n)*T + value of uniform random distribution;

END;

STEP 3: Making Envelop of received Rayleigh Signal

Performing Quadrature amplitude demodulation for signals;

E ^ sqrt (9i^N2 + 9q^2);

STEP 4: Computation of Outage probability

FOR X:= 1:P

Calculate the value of ρ;

Calculate the value of δ;

count = 0;

FOR Y = 1:length(E)

• power = power in decibel;

• 2.2 Simulation Results for Rayleigh Channel

IF power <= ρ count++

ELSE

END;

END;

Find the simulated outage probability;

END;

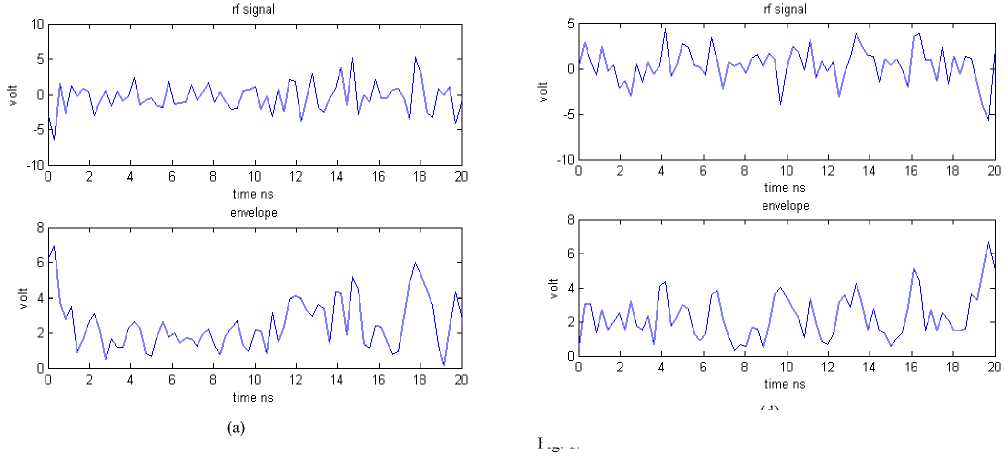
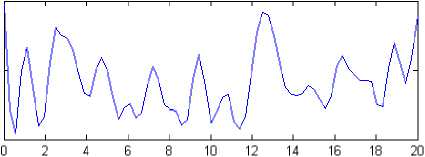
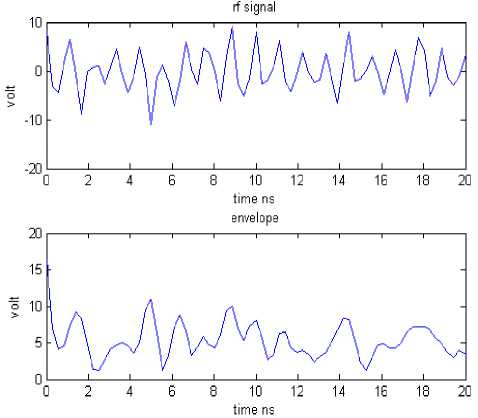
Figure 1, shows the RF signal and its envelop plot. As the speed of the user is increased from 0 m/s to 50 m/s, we can see that the amount of fading is increased in the signal envelop. In this simulation, we have set the threshold to 2.3 volt. As we increase the speed, more of the signal goes below the threshold. Hence the fading is one of the major problems in case of wireless communication.

(d)

Fig. 1: Simulated radio frequency signal by using proposed algorithm for Rayleigh fading channel for

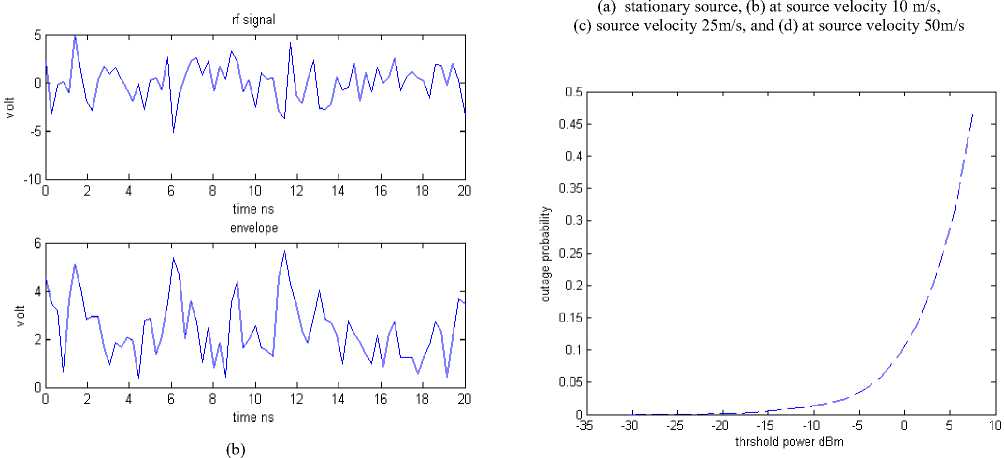
Fig. 2: Outage probabilities for the Rayleigh fading channel

rf signal

time ns envelope

0     2     4      6     8     10    12    14     16    18    20

time ns

(c)

The outage probability is the ratio of the number of samples of the signal below the threshold to the total number of samples. From Fig. 2, it is clear that as we increase the threshold power, the outage probability is increased, that is the probability of better detection of signal is decreased. A key requirement for such resource management schemes is to have an analytical model that can estimate the bit-error-rate and outage probability at high vehicular speeds, so that proactive actions can be taken and proper planning can be done. However, the fading models are used for the bit error rate and outage probability estimation. The fading channel caused by multipath and Doppler shift and often modelled with the popular Rayleigh distribution [21]. The Rayleigh fading model has not been challenged until very recently when researchers started to focus on high throughput at vehicular speeds. The Rayleigh model works on the assumption that the resultant fading arises from a large number of uncorrelated partial waves, with identically distributed amplitudes, and uniformly [0, 2n] distributed random phases [19,21]. This assumption is highly optimistic in a mobile communication environment at high vehicular speeds.

• III. Rician Fading Channel Model

When there is line-of-sight, direct path is normally the strongest component goes into deeper fade compared to the multipath components. This kind of signal is approximated by Rician distribution [4,19,20]. As the dominating component run into more fade the signal characteristic goes from Rician to Rayleigh distribution [16,19]. The derivation of the probability density function of the amplitude is more involved than for Rayleigh fading, and a Bessel function occurs in the mathematical expression. In the presence of such a path, the transmitted signal can be written as:

s (t) = EEa cos(act+(oa+^i) + kd cos(toct + rodt)

where the constant k d is the strength of the direct component, ω d is the Doppler shift along the line-of-sight path, and ω di are the Doppler shifts along the indirect paths. The envelope in this case has a Rician density function given by [4, 11]:

r

—e

f ⁽ r ) =

a

2 ^e

where I ₀ (0) the 0^th order is modified Bessel function of the first kind

• 3.1    Proposed Algorithm for Rician Channel

In this section, we have developed an algorithm for the Rician fading channel. The proposed algorithm completes its functioning in four different steps where step-1 declares about the various used variables in the proposed algorithm and step-2 is associated with the sending of data through the Rayleigh fading channel. In step-3 an envelope is designed for received Rayleigh signal using QAM amplitude demodulation on received signals. Finally, the step-4 calculates the outage probability using theoretical and simulated methods

Algorithm: Rician Fading Channel

STEP 1: Variable Declaration

• V: Input Velocity in miles/sec.

P: Input number of paths

T: Time array

Λ: Carrier frequency

• D:    Data frequency

η: Sampling frequency

ω: Radian frequency

τ: Sampling periods

θ: Received Rician signals

ρ: Threshold power

δ: Threshold outage

σ: Weibull distribution function

• E:    Rician envelop

STEP 2: Sending of Data through Rayleigh Channel

• 9    ^ Make an array of zeros [T]

FOR I := 1 : P

Calculates the value of D;

D ^ 2*pi*V*Л*cos(for uniform random distribution);

Find the value of σ;

9 ^ 9 + a*cos(Л+n)*T + value of uniform random distribution;

END;

STEP 3: Making Envelop of received Rayleigh Signal

Performing Quadrature amplitude demodulation for signals;

E ^ sqrt (9i^N2 + 9q^N2);

STEP 4: Computation of Outage probability

FOR X:= 1:P

Calculate the value of ρ;

Calculate the value of δ;

count = 0;

FOR Y = 1 : length(E)

power = power in decibel;

IF power <= ρ count++

ELSE

END;

END;

Find the simulated outage probability;

END;

3.2 Simulation Results for Rician Channel

rf signal

10--------1---------1---------1--------1--------т—

•10

0     2     4     6     8     10    12    14    16    18    20

time ns envelope

time ns

(c)

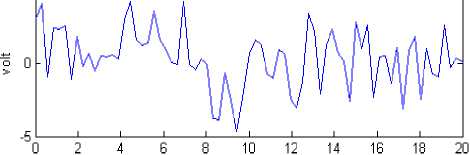
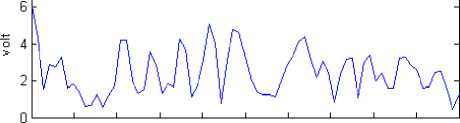
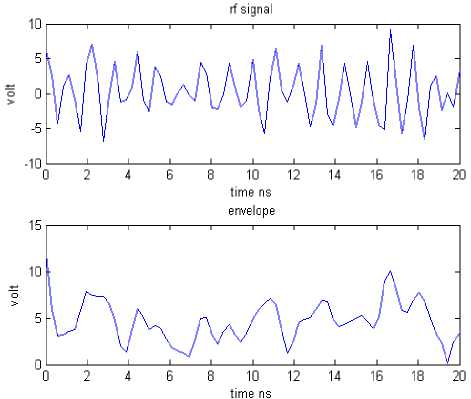
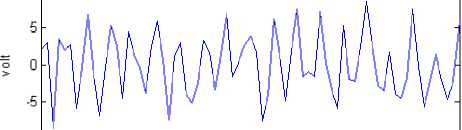
Figure 3, illustrate the RF signal and its envelop plot for Rician fading channel. As the speed of the user is increased from 0 m/s to 50 m/s, we can see that the amount of the fading is increased in the signal envelop. However, the threshold has been set to 2.3 volt. As we increase the speed, more of the signal goes below the threshold. Hence the fading is one of the major problems in case of wireless communication.

(a)

(d)

rf signal

10---------1---------1---------1---------1---------1—

•10---------------------------111---------------------------1----------------------------1---------------------------1---------------------------1----------------------------1---------------------------1----------------------------

"0     2     4     6     8     10    12    14      16     18    26

time ns envelope

10--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------

Fig. 3: Simulated radio frequency signal using proposed algorithm for Rician fading channel for

(a) stationary source, (b) at source velocity 10 m/s, (c) source velocity 25m/s, and (d) at source velocity 50m/s

П--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------1--------------------

"0     2     4     6     8     10    12    14     16    18    20

time ns

(b)

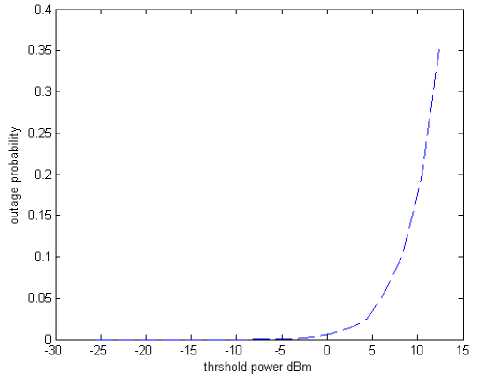
Fig. 4: The outage probabilities for Rician fading channel

The outage probability is the ratio of the no of samples of the signal below threshold to the total number of samples. From Fig. 4 it is clear that as we increase the threshold power outage probability is increased, that is probability of better detection of signal is decreased. In TABLE 1, the performance of the Rayleigh and Rician fading channel model has been compared. However in both cases (Rayleigh and Rician fading model) the outage probability increases with the increase of the velocity of the moving object.

Table 1: Performance comparison with reference to the outage probability of Rayleigh and Rician fading channels

Mobile velocity (in m/s)	Outage Probability (Rayleigh)	Outage Probability (Rician)
0	0.19149	0.09311
2	0.19193	0.09312
4	0.19246	0.09314
6	0.19303	0.09346
8	0.19339	0.09350

• IV. Conclusion

In this paper, we have simulated the Rayleigh and Rician fading channel models in vehicular environment for the outage probability. From the simulation results, we conclude that as the vehicle speed of user is increased, the amount of fading is increased in the signal envelope. Therefore, as we increase the speed, more of the signal goes below the threshold and the amount of fading increased. We also simulate the Rayleigh and Rician fading channels in terms of the outage probability by using Matlab simulation for different thresholds of the received signal and compare these values to those calculated analytically. However, the results from both the simulation and analysis are comparable. As we have observed from the comparison table, the outage probability in the Rician fading channel is lower than that of the Rayleigh fading channel, which is due to the presence of line-of-sight path in the Rician channel. We also concluded that the outage probability increases as the mobile velocity or Doppler shift increases. Dynamically changed multipath and Doppler effects are the main causes behind the degradation of the channel capacity. However, we would like to develop a generic model for fading in mobile communication (vehicular applications) system, which will be reported in future communication.

Acknowledgements

The authors are very much thankful to the potential reviewers for their critical comments and suggestions to improve the quality of the manuscript.