Performance Comparison of OFDM, FBMC, and UFMC for Identifying the Optimal Solution for 5G Communications
Автор: Sourav Debnath, Samin Ahmed, S.M. Shamsul Alam
Журнал: International Journal of Wireless and Microwave Technologies @ijwmt
Статья в выпуске: 5 Vol.13, 2023 года.
Бесплатный доступ
The fifth generation (5G) wireless technology has a significant impact on individuals' lives and work, and this impact is expected to increase in the future. The Orthogonal Frequency Division Multiplexing (OFDM) method, which is currently used in fourth generation (4G) technology, has limitations in meeting certain criteria such as data rates and speed for the latest technology due to issues such as sideband leakages, high Peak-to-Average Power Ratio (PAPR), and poor spectrum utilization. Additionally, the increasing demand for Internet of Things (IoT) and user-centric processing makes the OFDM method impractical. As a result, alternative technologies are being explored to meet these needs. Filter Bank Multicarrier (FBMC) and Universal Filtered Multicarrier (UFMC) are potential candidates for 5G technology. This paper focuses on the evolution of FBMC from OFDM, and then compares the performance of FBMC and UFMC by analyzing various modulation schemes such as Quadrature Amplitude Modulation (QAM), Phase Shift Keying (PSK), PAPR, and Bit Error Rate (BER) through Additive White Gaussian Noise (AWGN) and Rayleigh fading channels. A theoretical BER model is also established to validate the simulated BER results. In this paper BER is analyzed in terms mathematical and simulation based approaches. To validate this simulation based method, it can be compared with the theoretical BER results to verify the accuracy of this simulation. Result portays that, the theoretical results and the simulated results are quite close through the Additive White Gaussian Noise (AWGN) channel.
5G Technology, OFDM, FBMC, UFMC, QAM, PSK, PAPR, AWGN channel, Rayleigh Fading channel, BER
Короткий адрес: https://sciup.org/15019227
IDR: 15019227 | DOI: 10.5815/ijwmt.2023.05.01
Текст научной статьи Performance Comparison of OFDM, FBMC, and UFMC for Identifying the Optimal Solution for 5G Communications
Technology continues to advance at a rapid pace and this is particularly evident in the field of wireless communication. Many people rely on fast, efficient networks in their daily lives and 5G technology has been developed in response to these needs. Different types of systems such as Machine Type Communications (MTC), the Internet of Things (IoT), and Vehicle Communications (URLLC) are driving the transition from 4G to 5G networks in order to improve performance and create new research opportunities in the field of communication systems [8]. Currently, multi-carrier technology, specifically Orthogonal Frequency Division Multiplexing (OFDM), is widely used for data transmission. 5G offers fast data rates, low latency, excellent energy efficiency, and support for a large number of connected devices. It is particularly well-suited for short burst communications and is more resistant to time-frequency misalignments. Through the use of Multiple Input Multiple Output (MIMO) technology, 5G has shown the potential to provide 10 times better performance than 4G.
However, it should be noted that some developing countries may still rely on 4G networks due to infrastructure limitations. The advancement of wireless communication began with the fourth generation (4G), which introduced the Orthogonal Frequency Division Multiplexing (OFDM) modulation system for efficient bandwidth, immunity to multipath fading, and inter symbol interference (ISI). However, there are significant disadvantages to OFDM that make it unsuitable for the next generation of wireless technology, known as 5G. The use of a cyclic prefix in OFDM reduces efficient spectral usage, and the OFDM spectrum has high out-of-band side lobes which lead to low spectral efficiency. To address these limitations, multi-carrier modulation techniques such as Filter Bank Multicarrier Modulation (FBMC) and Universal Filtered Multicarrier (UFMC) have been proposed as alternatives. FBMC is a sub-carrier filtering technique that increases spectral efficiency and allows for sound localization in both time and frequency [1, 2]. It also has good channel capacity and reduces redundancy in transmission. However, FBMC has high computational complexity and introduces symbol overlapping in the time domain, making it less suitable for low-latency communication in the uplink and energy-saving communication systems [9, 10]. UFMC, on the other hand, filters subcarrier groups (sub-bands) rather than individual subcarriers, reducing filter length and minimizing time [6]. This makes UFMC more suitable for short burst communications and offers high spectral efficiency and reduced sidelobe attenuation compared to OFDM and FBMC.
The main focus of this paper is to study the evolution of the Filter Bank Multicarrier (FBMC) technique from the Orthogonal Frequency Division Multiplexing (OFDM) technique, and to investigate the impact of filter variation on the Universal Filtered Multicarrier (UFMC) technique through the use of Additive White Gaussian Noise (AWGN) and Rayleigh Fading channels. Various modulation techniques such as Quadrature Amplitude Modulation (QAM) and Phase Shift Keying (PSK) will be applied, and the resulting Bit Error Rate (BER) and Peak to Average Power Ratio (PAPR) will be analyzed and compared based on their characteristics. In addition, a theoretical BER model will be established to confirm the validity of the simulated results. Moreover, this paper shows the contribution on existing research on 5G communication systems and assist in the development of efficient and reliable communication solutions for future networks.
2. Related Work
With the incremental demands of multimedia and IoTs, significant research works have been conducted to compare the performance of multicarrier techniques to ensure a higher data rate with lower bit error..
Arun, Shikha proposed a new FBMC-OFDM transmission scheme where the PHYDYAS filter was used on all subcarriers. They showed that the performance of BER is better for smaller Carrier Frequency Offset (CFO) than higher CFO and the BER performance is not effective in 0 dB to 5 dB for complexity [1].
Hao Lin tried to identify why people still prefer Orthogonal Frequency Division Multiplex (OFDM) instead of FBMC and proposed a Filter-Bank OFDM (FB-OFDM) method. He used the complex-valued QAM symbols and map them. [2].
A novel method has been proposed that is based on the polynomial fitting characteristic of a high-power amplifier (HPA) and provides theoretical Bit Error Rate (BER) expressions for any HPA model [3].
Na Dongjun and Kwonhue Choi proposed a new system which achieved low Peak to Average Power Ratio (PAPR) in Filter Bank Multi-Carrier (FBMC) based on the Identically-Time-Shifted-Multicarrier (ITSM) condition and Discrete Fourier Transform (DFT) spreading technique. Their proposed scheme resulted in a significant PAPR reduction, specifically a 3 dB reduction, with a block size of W = 8, due to the incorporation of DFT spreading.[4].
Nissel and Rupp proposed a framework for the calculation of bit error probability in double selective Rayleigh fading channels utilizing m-Quadrature Amplitude Modulation or √m-Pulse-Amplitude Modulation (PAM) signal constellations. The framework was applied to a Vehicular A channel with a Hermite prototype filter, which resulted in a performance improvement over Orthogonal Frequency Division Multiplexing (OFDM) and a low BEP [5].
Sidiq, Mustafa, Seikh, and Malik designed a waveform having great spectral efficiency and less PAPR. They used QAM technique and subcarriers which are distinct to evaluate the PAPR of OFDM, FBMC, UFMC, etc. [6].
Least Square (LS) and Minimum Mean Square Error (MMSE) were two distinct techniques for channel estimation that could be applied to Ultra-Wideband Filter-Bank Multi-Carrier (UFMC) systems. Additionally, interpolation techniques such as Linear and Spline were also evaluated for UFMC. The results of simulations indicated that MMSE yields superior Mean Squared Error (MSE) performance compared to LS, as LS is more susceptible to noise at higher Signal-to-Noise Ratios (SNRs). It was also observed that a floor in MSE occurs in Additive White Gaussian Noise (AWGN) and Rayleigh fading channels. [7].
The authors presented a hardware platform for a Ultra-Wideband Filter-Bank Multi-Carrier (UFMC) transmitter. The proposed platform utilizes actual hardware to implement simplified methods for Inverse Fast Fourier Transform (IFFT), filtering, and spectrum shifting. This approach allows for an efficient overall architecture of the transmitter without the need for a large number of resources from a Field-Programmable Gate Array (FPGA). [8].
Wei, Li, Zhang and Cheng’s research comprehensively evaluated the performance of a Ultra-Wideband FilterBank Multi-Carrier (UFMC) system in terms of various metrics such as Spectral Efficiency (SE), Bit Error Rate (BER),
Peak-to-Average Power Ratio (PAPR), Carrier Frequency Offset (CFO), and in different multipath fading channels, as well as time delay effects (TD) [10].
3. System Model
In OFDM, several complex-valued subcarriers are modulated in each symbol period. Let the message signal, Xl [k] denote the lth transmit symbol at the k h subcarrier, where l = 0, 1, 2...., да and k = 0,1,2,... , TV — 1 . N denotes the total number of subcarriers. Because of the Serial to parallel conversion, the transmission time for N symbols is extended to NTs , which forms a single T sym length OFDM symbol. Ts is the symbol duration to maintain the orthogonality among the subcarrier signals. Consider, Tsym = NrTs. The lth OFDM signal at the kth subcarrier can be expressed as [11]:
{
0< t< T sym elsewhere
Then the baseband OFDM signal in the continuous time domain can be expressed as:
Xi(t) = ^oSXiM ei2^-lTsy^
The complex time domain sequence is then generated using IDFT and a cyclic prefix, and it is sent over the channel. The continuous-time baseband signal at t = lTsym + nTs with Ts = Tsym/N and fk = k/ Tsym to obtain the discrete time OFDM symbol. Thus, the following equation can be written as [11]:
xn £ k=o Xl\k\e''2T for n = 0, 1, . . ., N -1 (3)
where, Xk is complex symbol transmitted over the kth subcarrier. Off-set Quadrature amplitude modulation (OQAM) in FBMC is used in place of QAM, where the complex value of the QAM symbol is split into a real and imagined component that provides individual real valued symbols. Instead of utilizing cyclic prefix, FBMC uses filter and each subcarrier modulated signal passes through a filter. The prototype filter is PHYDAS filter. In FBMC-OQAM system, after channel coding and symbol mapping of serial high-speed data OQAM is used to modulate symbols. The purpose of OQAM pre-processing is to keep orthogonality between subcarriers and also it processes complex symbols in real and imaginary part. Let consider the sender signal is [12]:
x k,n a k,n + j b k,n
After the OQAM modulation and filtered the signal, the FBMC-OQAM transmitted signal can be specified as:
X(t) = Zm-=1oSn[flm,nh(t) + }bm,nh (t — 0 e^'—'' \
where, am , n is the real part and bm , n is the imaginary part of QAM symbol, hT (t) is prototype filter and T = —. The impulse response of the PHYDAS filter in frequency domain is [12]:
H(D I k 1 :. . И к
sin(n(f-—^Nk)
N ksin(n(f-±^
where, К is the overlap factor of the prototype filter, T is the sampling period, Ик is the coefficient of the prototype filter. In UFMC, group of subcarriers (sub-bands) are filtered. In UFMC system, each the modulated data stream passes through a series to parallel block, an N-size IDFT block, and finally an L-length filter block. UFMC transmitted signal in the time domain is the sum of the signals of all sub-bands, B. The following equation is [13]:
x(t^ = ^ i=1 FikVik a ik
where aik represents the modulated signal for the ith sub-band, Vik represents the IFFT to eplitz matrix of the Ith subband and its size is (N x ni ) and Fi is filter applied to the i th sub-band and this vector size is (( N + L- 1 ) *N) . In UFMC, sub-bands are performed, which are made up of subcarriers and entire group of subcarriers are filtered. Zero padding is used for unallocated carriers at the receiving end. Let, for the kth user, total number of sub-bands is Bk and the total number of subcarriers is Nk . Consider in the i th sub-band there are Ni subcarriers. So, 2f^iVi = Nk . Ni
complex symbols sequence is transformed into a block of Nl parallel symbols and Td is the duration of each block. Let xkl be the data vector of the k‘ h user in the ith sub-band. The baseband signal of the kth user may be expressed as:
xk(f) - ^^Х™ 1-1 x^n) e!2nnT a hkl (t - nTd) (8)
where, hkl(t) indicates the filter function utilized in the ith sub-band for the kth user. The Chebyshev’s filter response function is [15]:
h l,k
cos [Ncos 1 (ficos (tt ^ ))]
cosh[Ncos h 1 (P)]
;0 ^ = cosh[1 cos h 1(10“)] and a represents attenuation of the side lobe. Hence, there is needed power for transmission which is represented as PAPR (Peak-to-Average Ratio). The maximum power ratio of a transmitted signal to the mean power of the signal is known as Peak-to-Average Ratio (PAPR). With a multi-career system, PAPR tends to happen when the many subcarriers are out of phase. The PAPR of the OFDM, FBMC, and UFMC is [11]: PAPR = max ter {Ы2} E { l^nl2} where, т is time interval, max t e T { |xn|2} is peak signal power and E { |xn|2} is average signal power. The signal is transmitted through additive gaussian white noise channel (AWGN) and Rayleigh Fading channel. Because of bit loss in the air, ISI, overlapping, and other factors, sending and receiving bits are not equal to transmitting bits. As a result, the bit error rate is computed, and it is preferable to keep the bit error rate for the signal as low as possible. For OFDM, FBMC, and UFMC, the theoretical BER equation of QAM and PSK modulation schemes is [11-15]: BEROFDM(QAM) 2(^M-1) ^M log2^M Q log2^M M-1 ) BEROFDM(PSK) 6Eb No = Q BERFBMC (QAM) 1yK2(VM-1) N ^'l=1^M log2^M (J 3log2 (M)Eb Wkl2K 4N0(M-1)T(ok2+ od2 ) BERFBMC (PSK) - N T^1 Q (j2No'Tb(^+^--) BERUFMC (QAM) 1в В yK 2(^M 1) ( I6Eb । ~ 12 log2^M KB 4=1=^ Lk^ JM log2VM ^ \\ No ' k' ' M-1 where, M represents modulation order, rk represents the filter response, ok2 represents variance of AWGN and od represents the NL distortion, Eb/No represents the signal to noise ratio, T represents symbol duration time.
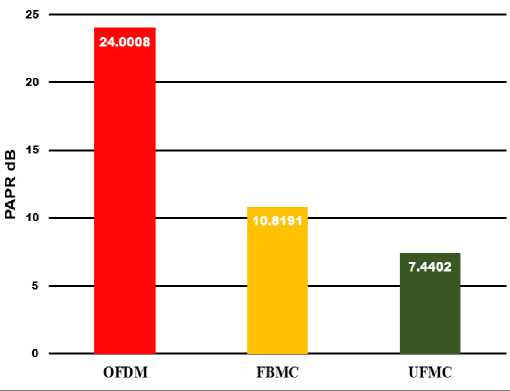
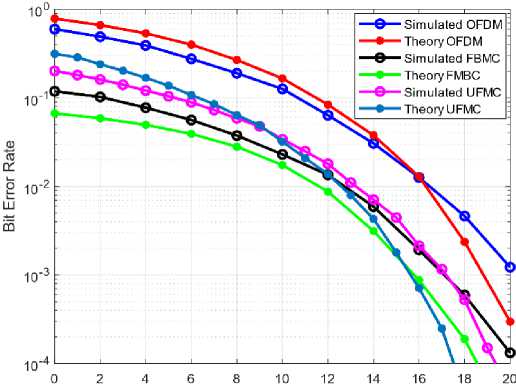
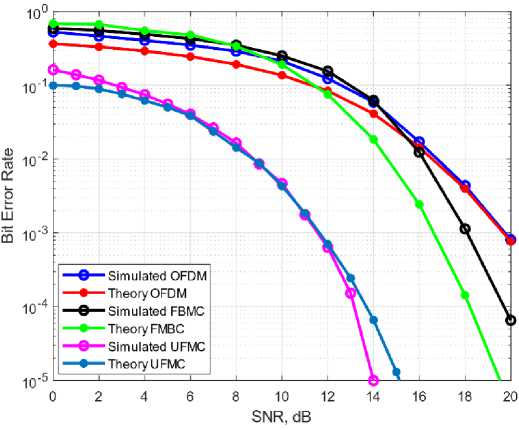
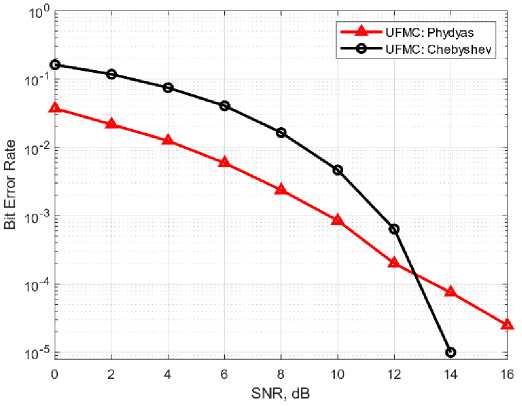
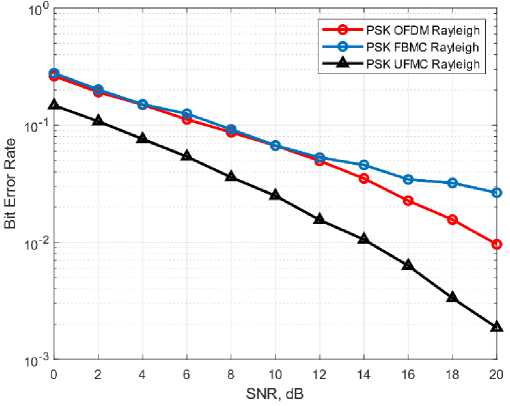
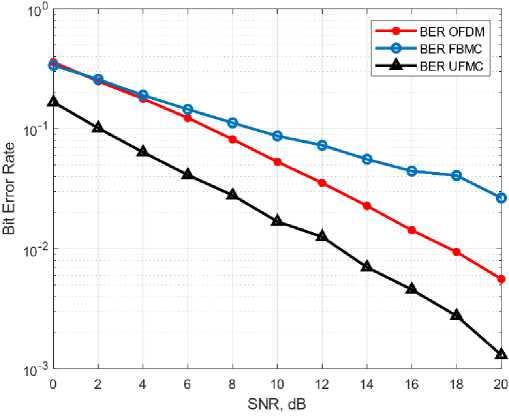
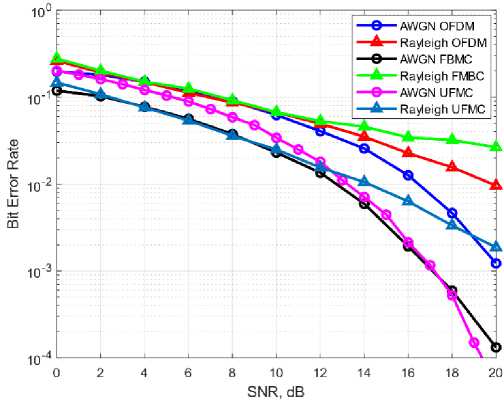
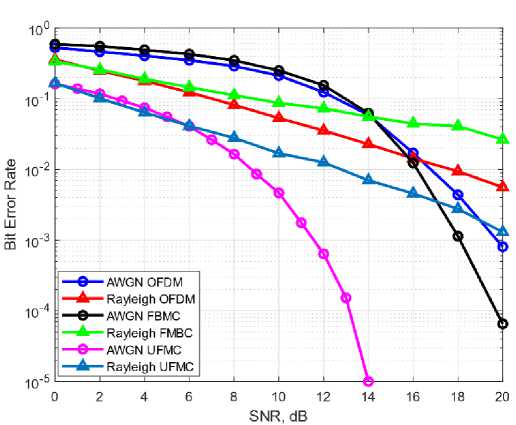
4. Simulation Results This section is divided into three parts. The first part involves measuring the Peak to Average Power Ratio (PAPR) value at the transmitting end for a fixed number of subcarriers. In the second part, various modulation schemes such as Quadrature Amplitude Modulation (QAM) and Phase Shift Keying (PSK) are employed for 400 subcarriers to evaluate the Bit Error Rate (BER) performance through Additive White Gaussian Noise (AWGN) and Rayleigh fading channel. The Discrete Fourier Transform (DFT) mechanism and frequency sampling technique are applied in the design of filters for Filter Bank Multi-Carrier (FBMC) and Universal Filtered Multi-Carrier (UFMC) systems. Finally, simulated results are compared with theoretical models using equations 11 to 15. The simulation environment utilized in this study is MATLAB 2018b. Table 1 presents some of the key simulation parameters to provide a clear understanding of the simulated environment. In Figure 2, a comparison of Bit Error Rate (BER) performance is presented using the Phase Shift Keying (PSK) modulation scheme among Orthogonal Frequency Division Multiplexing (OFDM), Filter Bank Multi-Carrier (FBMC), and Universal Filtered Multi-Carrier (UFMC) systems. The BER performance of PSK modulation is found to be inadequate. The BER is at 10-4 near 20 dB in UFMC and approximately 10-4 at 20 dB in FBMC. However, in OFDM, the BER is approximately 10-3 at 20 dB, which is significantly worse in comparison to FBMC and UFMC. Furthermore, FBMC and UFMC show similar performance in PSK, which may not be suitable for high-speed data communication. Additionally, the power consumption in these systems is also relatively high. Table 1. Parameter Defination Chart Fig. 1. The PAPR values of OFDM, FBMC, UFMC system. Fig. 2. The BER of OFDM, FBMC, and UFMC using PSK. SNR, dB Symbol Parameters Value OFDM FBMC UFMC No. of subcarriers 400 400 400 CP Length 30 × × FFT size 512 512 512 Filter type × PHYDYAS Chebyshev, PHYDYAS Overlapping Factor × 2 × No. of sub bands × × 20 Sub bands size × × 20 In Figure 3, the performance comparison results for Additive White Gaussian Noise (AWGN) channel are presented. It is observed that compared to Orthogonal Frequency Division Multiplexing (OFDM) and Filter Bank Multi-Carrier (FBMC), Universal Filtered Multi-Carrier (UFMC) system exhibits superior Bit Error Rate (BER) performance. The length of the filter in UFMC is the same as the cyclic prefix length of OFDM, and the BER is relatively low as well as the power consumption is also lower compared to OFDM and FBMC. In UFMC, the number of errors is presented as a ratio such as 1 in 100,000 or 1 in 1 × 10-5, whereas OFDM and FBMC required significantly higher Signal-to-Noise Ratio (SNR) power for achieving lower BER performance. For example, as shown in Figure 3, the BER is 10-5 at near 14 dB in UFMC. In contrast, the BER is 10-4 in FBMC and 10-3 in OFDM at near 20 dB. In this proposed system, it is possible to lower the transmit power by saving 6dB by reducing the SNR compared to OFDM and FBMC. From Figure 2, it is evident that, when using the Phase Shift Keying (PSK) modulation technique, the theoretical Bit Error Rate (BER) of Orthogonal Frequency Division Multiplexing (OFDM), Filter Bank Multi-Carrier (FBMC), and Universal Filtered Multi-Carrier (UFMC) systems at 14 dB are 2.51 × 10-2, 3.54 × 10-3, and 3.16 × 10-3 respectively, while the simulated results of these systems are 2.49 × 10-2, 3.98 × 10-3 , and 3.71 × 10-3 respectively. Fig. 3. BER performance of OFDM, FBMC, UFMC using QAM. Similarly, from Figure 3, the corresponding theoretical values of OFDM, FBMC, UFMC using Quadrature Amplitude Modulation (QAM) technique at 14 dB are 1.95 × 10-2, 1.26 × 10-2, and almost 10-5 respectively. The simulated results of these systems are 1.76 × 10-2, 1.5 × 10-2, and 10-5 respectively. Therefore, it can be inferred that, the theoretical results and the simulated results are quite close through the Additive White Gaussian Noise (AWGN) channel. By comparing the simulated results and theoretical results in Figure 2 and Figure 3, it can be concluded that, there is a strong agreement between the theoretical and simulation results, and hence, the theoretical and simulated models are accurate for the AWGN channel. Fig. 4. BER performance of UFMC using PHYDYAS and Chebyshev filter. As depicted in Figure 4, the Chebyshev filter exhibits satisfactory performance in the Universal Filtered MultiCarrier (UFMC) system when compared to the PHYDYAS filter. Additionally, the power requirement is lower in the Chebyshev filter. It should be noted that the length of the PHYDYAS prototype filter is the same as the Chebyshev filter. Fig. 5. BER Performance of OFDM, FBMC, UFMC using PSK through Rayleigh Channel. Fig. 6. BER Performance of OFDM, FBMC, UFMC using QAM with 10 Tap Rayleigh Channel. Figure 5 and Figure 6 illustrate the Bit Error Rate (BER) of Orthogonal Frequency Division Multiplexing (OFDM), Filter Bank Multi-Carrier (FBMC), and Universal Filtered Multi-Carrier (UFMC) systems in a 10 tap Rayleigh fading channel with various modulation techniques. In Fig. 6, Rayleigh channel is a model used to simulate the time-varying effects of a wireless communication channel which assumes that the received signal is a random variable that varies in amplitude and phase due to the multipath propagation of the signal. Moreover, in a 10-tap Rayleigh channel, the channel impulse response is modeled as a sum of 10 complex exponential functions with different amplitudes, phases, and delays. Each tap represents a different path that the signal can take from the transmitter to the receiver, with a different delay and attenuation. It is evident from the figures that the results are logical. However, there is a difference in the curves of FBMC and UFMC at various modulation techniques. Due to the interference of additive noise, the BER of FBMC and UFMC in the Rayleigh channel gives poorer performance than that in the Additive White Gaussian Noise (AWGN) channel. For instance, when using the Quadrature Amplitude Modulation (QAM) technique, at 14 dB, the BER of UFMC in the Rayleigh Fading Channel is 5.012 x 10-3 whereas, in the AWGN channel, the BER is 10-5. The same case is observed in the Phase Shift Keying (PSK) modulation process. Additionally, the power dissipated in the Rayleigh channel is enormous compared to the AWGN channel which is not consistently good in performance. Fig. 7. BER Performance of OFDM, FBMC, UFMC using PSK through AWGN and Rayleigh Channel. Fig. 8. BER Performance of OFDM, FBMC, UFMC using QAM through AWGN and Rayleigh Channel. Figure 7 and Figure 8 portay the comparison of error rate of OFDM, FBMC and UFMC using PSK and QAM through AWGN and Rayleigh Channel. In these figures, it is shown that modulation techniques such PSK plays poor performance over QAM due to the constellation mapping of data signals. From the above analysis it is important that the choice of a modulation technique depends on the specific requirements of the communication system such as BER, PAPR, and robustness to channel impairments. Moreover it depends on spectral efficiency and power efficiency etc. which is be discussed in the future works in this paper. However, In terms of BER performance, the response of UFMC over OFDM and FBMC is better over both AWGN and Rayleigh channel. But this superiority of UFMC over OFDM and FBMC is not a universally accepted fact, and it depends on various factors such as in high-mobility or low mobility environments. Here, Doppler spread is not analyzed which is the significant limitation of this paper.
5. Conclusion In this paper, a comprehensive evaluation and comparison are made between various modulation techniques, including Orthogonal Frequency Division Multiplexing (OFDM), Filter Bank Multi-Carrier (FBMC), and Universal Filtered Multi-Carrier (UFMC) in terms of Peak to Average Power Ratio (PAPR) and Bit Error Rate (BER). Additionally, the performance of PHYDYAS and Chebyshev filters in UFMC is also investigated, and it is shown that the Chebyshev filter provides better performance. Based on the simulation results of PAPR, transmitting power, and BER of the multicarrier techniques, it can be concluded that UFMC is a promising candidate for 5G technology. It increases spectral efficiency, reduces sidelobe attenuations, and inter-symbol interference (ISI), making it more beneficial for future network technologies. It is possible to optimize further in the future to convert to Generalized Frequency Division Multiplexing (GFDM) for its flexibility, efficient use of the Cyclic Prefix (CP) in short packet transmissions, and low out-of-band radiation to minimize unwanted interference. GFDM combines subcarriers and sub-symbols to create a circularly pulsed waveform. With its additional Space-Time-Coding (STC) method, GFDM is well-suited for low latency applications [16]. Research on GFDM is ongoing to achieve greater spectral efficiency than UFMC and potentially use it in future advanced technologies instead of UFMC. Although, UFMC has several advantages like lower out-of-band radiation, and better robustness to channel impairments. In this paper, theoretical and practical Simulations are introduced to evaluate the performance of different modulation techniques such as OFDM, FBMC, and UFMC for different parameters like BER, PAPR, QAM, and PSK over AWGN and Rayleigh fading channels. These simulations are also useful for exploring new ideas and concepts before investing in costly hardware development and testing. On the other hand, hardware implementation of these systems refer to the actual deployment of communication systems using physical hardware and real-world channel conditions. In real world, hardware implementation is more challenging and complex compared to simulation. But the outcome from the simulation will give the expected result of the communication system implemented in the real world scenario.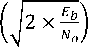
Список литературы Performance Comparison of OFDM, FBMC, and UFMC for Identifying the Optimal Solution for 5G Communications
- A. Kumar and S. Bharti, “Design and performance analysis of ofdm and fbmc modulation techniques,” The Scientific Bulletin of Electrical Engineering Faculty, vol. 17, 10 2017, doi: 10.1515/sbeef-2017-0007.
- H. Lin, "Filter bank OFDM: A new way of looking at FBMC," 2015 IEEE International Conference on Communication Workshop (ICCW), 2015, pp. 1077-1082, doi: 10.1109/ICCW.2015.7247320.
- Bouhadda, H., Shaiek, H., Roviras, D. et al. Theoretical analysis of BER performance of nonlinearly amplified FBMC/OQAM and OFDM signals. EURASIP J. Adv. Signal Process. 2014, 60 (2014), doi: 10.1186/1687-6180-2014-60.
- D. Na and K. Choi, "Low PAPR FBMC," in IEEE Transactions on Wireless Communications, vol. 17, no. 1, pp. 182-193, Jan. 2018, doi: 10.1109/TWC.2017.2764028.
- R. Nissel and M. Rupp, "OFDM and FBMC-OQAM in Doubly-Selective Channels: Calculating the Bit Error Probability," in IEEE Communications Letters, vol. 21, no. 6, pp. 1297-1300, June 2017, doi: 10.1109/LCOMM.2017.2677941.
- S. Sidiq, F. Mustafa, J. A. Sheikh, and B. A. Malik, “Fbmc and Ufmc: The modulation techniques for 5g,” in 2019 International Conference on Power Electronics, Control and Automation (ICPECA), 2019, pp. 1–5, doi: 10.1109/ICPECA47973.2019.8975581.
- V. Durga and S. Anuradha, “On channel estimation in universal filtered multi-carrier (ufmc) system,” in 2019 PhotonIcs Electromagnetics Re- search Symposium - Spring (PIERS-Spring), 2019, pp. 3708–3713, doi: 10.1109/PIERS-Spring46901.2019.9017701.
- A. Jafra, J. Majid, L. Zhang, M. Imran, and M. Najam-ul islam, “Fpga implementation of ufmc based baseband transmitter: Case study for lte 10mhz channelization,” Wireless Communications and Mobile Computing, 09 2018.
- "Prototype Filter- an overview" https://www.sciencedirect.com/topics/engineering/prototype-filter.
- S. Wei, H. Li, W. Zhang and W. Cheng, "A Comprehensive Performance Evaluation of Universal Filtered Multi-Carrier Technique," in IEEE Access, vol. 7, pp. 81429-81440, 2019, doi: 10.1109/ACCESS.2019.2923774.
- Cho, Yong and Kim, Jaekwon and Yang, Won and Kang, Chung. (2010). MIMO-OFDM Wireless Communications with MATLAB®: Cho/MIMO-OFDM Wireless Communications with MATLAB®, doi: 10.1002/9780470825631.
- L. Yao, E. Wang, and X. Peng, “Design and research on fbmc-oqam multicarrier technology for 5g,” Journal of Physics: Conference Series, vol. 1213, p. 052068, 06 2019, doi: 10.1088/1742-6596/1213/5/052068.
- A. S. Rachini and M. M. Jaber, “Performance of fbmc in 5g mobile com- munications over different modulation techniques,” in 2019 International Symposium on Networks, Computers and Communications (ISNCC), 2019, pp. 1–6, doi: 10.1109/ISNCC.2019.8909111.
- H. Bouhadda, H. Shaiek, Y. Medjahdi, D. Roviras, R. Zayani and R. Bouallegue, "Sensitivity analysis of FBMC signals to non linear phase distortion," 2014 IEEE International Conference on Communications Workshops (ICC), 2014, pp. 73-78, doi: 10.1109/ICCW.2014.6881175.
- Kishore, K. K., Umar, P. R., and Naveen, V. J. Comprehensive analysis of UFMC with OFDM and FBMC, Indian Journal of Science and Technology, 10(17), 1-7, doi: 10.17485/ijst/2017/v10i17/114337.
- B. Lim and Y. Ko, "SIR Analysis of OFDM and GFDM Waveforms With Timing Offset, CFO, and Phase Noise," in IEEE Transactions on Wireless Communications, vol. 16, no. 10, pp. 6979-6990, Oct. 2017, doi: 10.1109/TWC.2017.2736998.


