Performance Comparison of Various Diversity Techniques using Matlab Simulation

Published Online October 2013 in MECS

Diversity combining is a potential method by which multiple replicas of the same information carrying signal received over several diversity branches are combined with specific manner in order to combat the diverse effects of the multipath fading in wireless communication systems [1-6]. However, the diversity combining methods have been implemented either at receiver or transmitter, or on both for combating very effectively the effects of multipath fading at a relatively low cost. For instance, let us consider the design of an antenna array receiver for the millimeter-wave communications, where several tens of array elements have been placed on the surface of a portable receiver [7-10]. Thus, there is a need for significant diversity combining techniques to be used effectively with large antenna arrays. However, the suboptimal receiver structures may exploit other statistics or consider a partitioned diversity combining scheme [10] to achieve the performance comparable to the optimal receiver. Then, it would be highly desirable to assess the efficacy of several receiver design options to obtain the most appropriate choice with reference to the complexity and implementation constraints.

Due to the time-varying nature of the wireless channel and presence of limited resources for transmission, the transmitted signal faces various detrimental effects such as path loss, delay spread, Doppler spread, shadowing and interference which make it very difficult to achieve high data rates. To mitigate the effect of multipath fading in the wireless communication, a most popular mechanism known as diversity has been introduced. In the telecommunication system, the diversity schemes is a method for improving the reliability of a message signal by using two or more communication channels with different characteristics. It plays significant role in combating the signal fading and co-channel interference without error bursts.

Alternatively, a redundant forward error correction code can be used. The diversity technique exploits the multipath propagation and provides the diversity gain (measured in decibels) [2-10]. The diversity combining technique can be exploited over time, frequency and space domains. However, it is well known that the diversity reception is an efficient communication receiver technique for mitigating the detrimental effects of multipath fading by increasing the overall signal-to-noise ratio (SNR) and improve the radio link performance in the wireless mobile channels at relatively low cost [11-21].

In this paper, we have developed an algorithm for the performance evaluation of various spatial diversity combing techniques by using Matlab simulation. The most important diversity reception methods employed in digital communication receivers are maximal ratio combining (MRC), equal gain combining (EGC), and selection combining (SC). However, MRC is the optimal technique in the sense that it attains the highest SNR as compared to any combining scheme as well as independent of the distribution of the branch signals since it results in a maximum-likelihood receiver. The remainder of the paper is organized as follows. Section 2 is concern with the diversity system model. In section 3, proposed algorithm for the performance evaluation has been developed. Section 4 discusses about the simulation results for various diversity techniques by using developed algorithm. Finally, section 5 concludes the work.

• II.    Diversity System Model

The diversity system model consists of a physical model by assuming the fading to be independent from one element to the next and each element acts as an independent sample of the random fading process (Rayleigh) means each element of the array receives an independent copy of the transmitted signal [9, 11]. In this system model, we emphasized to combine all these independent samples to yield the enhanced signal-to-noise ratio (SNR) and reducing bit-error-rate (BER). However, the diversity works because we receive N independent copies of the same signal at array of N antennas. If at least one copy has sufficient power, one should be able to process the signal. Here, we consider a single-user system model wherein the received signal is a sum of the desired signal and noise [2, 3].

x - hu ( t ) + n (1)

where u (t) is the unit power signal transmitted, h represents the channel (including the signal power) and n the noise. The power in the signal over a single symbol period, T _s, at element n , is

T ²

P ,! h n ¹ t )l u ¹ t )l ^dt s

= hn1t )l 1 flu1t )l dt = hn I2 1 s

Since we are assuming slow fading, the term |h n(t)| remains constant over a symbol period and can be brought out of the integral and u(t) is assumed to have unit power. Setting E[|n_n (t)|²} = a ² and we get the instantaneous SNR at the n th element (y_n) as:

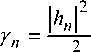
О

This instantaneous SNR is a random variable with a specific realization given the channel realization h . The expectation value taken to estimate the noise power is therefore consider over a relatively short time period [2]. We are assuming Rayleigh fading, so h n = \nn\^e j < h n where ^_n is uniform in [0, 2 л ] and |h_n | has a Rayleigh pdf, implying |A„J² and y_n has an exponential pdf such as [3]:

h n ²

Ihnl = 2^^е  p0

P ₀

1   -/,r у ~ __p ‘ n /r

Y n ~ r^ e

r- E { / , ) - E { h ^ = P 2 C    C

The instantaneous SNR at each element which is an exponentially distributed random variable. Г represents the average SNR at each element. This is also the SNR of a single element antenna that is the SNR if there is no array. Therefore Г serve as a baseline for improvement in the SNR.

• 2.1    Selection Combining Diversity

• 2.2    Maximal Ratio Combining Diversity

At the receiver, if we have now N copies of the same transmitted symbol. Then we have to combine them effectively to reliably recover the transmitted data. We consider the fading for each signal is independent. In the selection combining diversity, the receiver selects the antenna with the highest received signal power and ignores observations from the other antennas. We assign weights such that for maximum power signal provide weight 1 and for rest of others weight 0. Therefore, we are able to get one significant signal at the output. For deriving the mathematical expressions for the selection combining diversity, we obtain the set of weights w. To obtain the weight vector value, we assume that the receiver has the required knowledge of the channel fading vector h. As each element is an independent sample of the fading process, the element with the greatest SNR is chosen for further processing. In the selection combining diversity, the expression instantaneous SNR with weight function can be written as [2-5]:

1   Y k = max n { Y n }

0 otherwise

Since the element chosen is the one with the maximum SNR, the output SNR of the selection diversity scheme is Y = maX_H Y } ■ This technique requires only the measurement of the signal power no phase shifters and variable gain. The parameters for analyzing such systems are the outage probability, BER and resulting improvement in SNR. The outage probability provides the probability that the output SNR falls below a threshold value Y_s ■ This expression is valid only when the fading at each element is assumed independent. By using the pdf of Y _n , then the outage probability is [2, 8]:

P out ( Y s ⁾= [¹ - e ^Y s / ^{Г ] ^}                   (8)

From (8), the outage probability decreases exponentially with the number of elements. P represents the cdf of the output SNR as a function of threshold Y_s ■

In order to maximize the output SNR of the signal, we cannot choose one signal and neglect others. So we combine the signals on such a way that the output signal provides all transmitted information. In MRC, we assign the weighted bits to the signal in such a way that all the signals are strong, which is performed in the order to improve the faded signals. The branches with strong signals are further amplified and those which are week are attenuated. Then we combine the signals to get output signal, which improved the performance than the selection combining diversity, however it is too complex to implement. Its weighted bit allocation process is complex and we have to know the exact signal at the receiver [10, 16]. The received signal at the array elements as a vector x(t), and the output signal as r(t) [2, 3]:

x ( t ) = h ( t ) u ( t ) + n ( t )                           (9)

and r (t )= wH x = wHhu (t)+ wH n           (11)

Since the signal u(t) has unit average power, the instantaneous output SNR is:

Y =

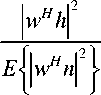
The noise power in the denominator is given by:

P = E {| w^Hn | } = E {| w^Hnn^Hw |}

= E { w H E { nn H } w } = ст² w H I _Nw

<7² w^Hw = ст ²|| w||                                (13)

and I _N represents the N×N identity matrix. Since the constants do not matter, one could always scale w such that ||w|| = 1. The SNR is therefore given by [2]:

w^Hh ²

^Y =

By the Cauchy-Schwarz inequality, it has a maximum value when w is linearly proportional to h, or w = h, then or

N - 1

Y = i Yn n=0

The output SNR is, therefore, the sum of the SNR at each element. However, the better diversity combiner can choose the weights to the fading for each element. In some sense, this answer is expected since the solution is effectively the matched filter for the fading signal. We know that the matched filter is optimal in the single user case. By using (15) expected value of the output SNR is therefore N times the average SNR at each element, which is [3]:

E { 7 } = N Г

fluctuate over several 10s of dB. In the equal gain combiner, [2]:

This indicates that on average, the SNR improves by a factor of N, which is significantly better than the factor of (lnN) improvement in the selection combining diversity case. To determine the pdf of the output SNR, we use the fact that the pdf of the sum of N independent random variables is the convolution of the individual pdfs. Further, the convolution of two functions is equivalent to multiplying the two functions in the frequency (or Laplace) domain. We know that each in  (15)  is exponentially distributed. The characteristic function of a random variable X is given by E {e sX} that is, the characteristic function (the

Laplace transform) of the pdf.

wn = eJ < hn(24)

Wn * hn = hn| wH h = NZ1hn\(26)

n = 0

The noise and instantaneous SNR are given by:

Pn = wHwa2 = Na2

F n ( s ) = E {г- ^{S Y n} } =

1 + s Г

F r ^{( s} ) =

1   1 N

1 + s Г

7 =

~ N - 1   1²

Z hln \

_ n = 0    i

N a ²

PDF ( 7 ) = f r ( 7 ) = L - [ F -( s ) 1

1 c + j ”     e s                 ⁽²⁰⁾

= 2 П / ' c -J” ( 1 + s r ) ^N7 or

N - 1

PDF ( у ) = ₇---- _? "— e ^{- 7} / ^Г            (21)

(N -1)! Г N

Using the fact that h is Rayleigh distributed, we have:

E ( НД ) =7n P 0"                            (29)

E [| h n ² ) = P o                                (30)

By using the SNR defined in (28) together with (29) and (30), we can find the mean SNR as:

Using this pdf, the outage probability for a threshold

7 _s is given by [3]:

E {"} =

N - 1

E ( Zl h n\

n = 0

P out = ^P ( 7 <  7 , )

2 N a¹

= Г

1      " N ^{- 1}

( N - 1 ) ! Г ^N

e ^{7 / Г} d "

2 N a²

N - 1 N - 1

E kZI h n ll h . l

L n = 0 m = 0

P out = ¹

—

n = 0

- 7 , / Г e ^s

N - 1

Z

1 n !

After some mathematical manipulation and simplifying (31), we get:

E {У } =

1 + ( N - 1 ) П Г

• 2.3    Equal Gain Combining Diversity

  In this process, we have assigned the equal weights to the receiver branches which amplify the signals equally. With reference to the performance comparison it is comparable to MRC, however easy to implement [1621]. So it is a better option than the selection combining diversity. We require a technique in which the weights vary with the fading signals and the magnitude of which

This analysis reveals that, despite being significantly simpler to implement, the equal gain combiner results in an improvement in SNR that is comparable to that of the optimal maximal ratio combiner. The SNR of both combiners increases linearly with N .

• III.    Proposed Combined Algorithm for Diversity Techniques MRC, SC and, EG

In this section, we have proposed a combined algorithm for the discussed diversity techniques in the preceding sections like maximal ratio combining, selection combining and equal gain. The proposed algorithm completes its functioning in 12 different steps. User has to make the choice A, B, and C to implement the discussed diversity technique MRC, SC, and EG, respectively and based on the given choice algorithm computes the various operations which are listed in various steps for each diversity techniques. Finally, algorithm computes and compares the simulated outage probability/BER as well as SNR enhancement with the theoretical results.

Algorithm: Combined diversity techniques

STEP 1: VARIABLE DECLARATION

N: Number of bits or symbols ip: Matrix of [0,1]

S : Represents BPSK Modulation

X : input for number of receiver of antennas

Eb_No_dB : required signal to noise ratio in digital communication systems

• n : Additive white noise

• ii, jj : input of argument specifying the SNR in dB.

• h : Rayleigh channel

sD, y: Channel and noise addition nErr: Counting the number of errors.

ch: enter choice

STEP 2: Define Switch

SWITCH(ch)

ch == A : Maximal Ratio Combining (MRC)

ch == B : Selection Combining (SC)

ch == C : Equal Gain (EG)

if (ch == A)THEN

STEP 3: Functioning Of MRC Algorithm

N ^ Input;

generate matrix of [0,1] with equal probability ip ^ rand(1,N)>0,5;

find BPSK modulation S ^ 2 * ip -1 where 0 ->-1, 1 ^ 1;

input X;

Eb_No_dB ^ [0:35] for multiple values of Eb/No.

FOR jj ^ 1:length(nRx)

FOR ii ^ 1:length (Eb_No_dB)

Calculate white Gaussian noise n with 0 dB variance;

Make and Find the value of h;

STEP 4: Channel and noise addition sD ^ Kron(Ones (nRx (jj),1),S);

y ^ h.*sD + 10^(-Eb_No_dB (ii)/20)*n;

STEP 5: Equalization of MRC

Find the value of yHat;

STEP 6: Receiver hard decision decoding

Find the value if ipHat;

STEP 7: Counting of Errors

Find the value of nErr(jj,ii);

END

END

ELSEIF (ch == B)

STEP 8: Functioning of SC algorithm

REPEAT STEP 3 and STEP 4

STEP 9: Finding the power and max power of channel

Find the hPower and hMaxVal of the signal on all rx chain;

STEP 10: Delecting the chain with maximum power

Find the value of YSel and hSel;

REPEAT STEP 6 and STEP 7;

ELSE (ch==C)

STEP 11: Functioning of EG algorithm

REPEAT STEP 3 and STEP 4 ;

STEP 12: Equalization with EQUAL GAIN combining

Find the value of yHat;

REPEAT STEP 6 and STEP 7;

ENDIF

ENDIF

Calculate and compare simulated BER and theoretical BER;

• IV.    Simulation Results for Comparison of above Diversity Techniques

Fig. 1 shows the plot between signal-to-noise ratio and number of received antennas. As we increase the number of received antenna, the SNR is increased significantly. The above plot shows us that the MRC is the best among the three diversity techniques. Equal Gain combining technique is closest to the MRC and the Selection Combining is worst among them. In terms of the required processing, the selection combiner is the easiest - it requires only a measurement of SNR at each element, however not the phase or the amplitude. The results presented, used a coherent receiver (the phase of channel is removed after the fact). However, both the maximal ratio and equal gain combiners, on the other hand, require phase information. The maximal ratio combiner requires accurate measurement of the gain too. This is clearly difficult to implement, as the dynamic range of a Rayleigh fading signal may be quite large. For this additional cost, for two elements, the MRC improves performance by about 0.6dB over the equal gain combiner at a BER of 1%. Table 1 compares the various diversity techniques.

Table 1: Comparison of various diversity techniques

Technique	Circuit Complexity	C/N Improvement factor
Selection Diversity	N receivers	1+1/2+…+1/N
EGC Diversity	N receivers co-phasing	1+(N-1) π /4
MRC Diversity	N receivers co-phasing channel estimator	N

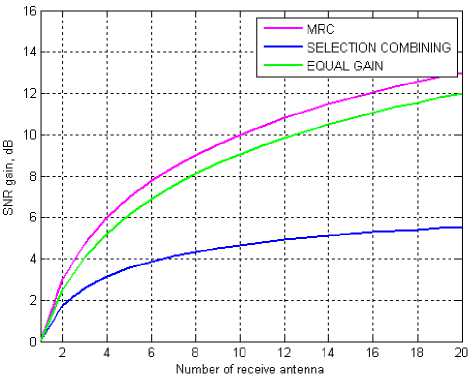
Fig. 1: Comparison of diversity combining techniques at receiver

• V.    Conclusion

The diversity combining techniques are one of the most significant solutions to mitigate the fading problem in the wireless communication systems. It overcomes the effects of flat fading by combining multiple independent fading. However, it entails some penalty in terms of rate, bandwidth, complexity or size. However, various combining techniques offer different level of complexity and performance. Among all the combining techniques, MRC offer the best performance, however the highest complexity, whereas the selection combining has the lowest performance and least complexity. These techniques are used to improve the performance of radio channel without any increase in the transmitted power. In this paper, we have developed an algorithm for the diversity combining techniques in MATLAB for the comparative analysis. We observed their performance by varying the number of receiver antennas and measuring the SNR at the receivers, which reveals that MRC is the best diversity among all three and selection combing is the worst. We can also observe that the equal gain is also close to MRC in terms of the performance. To compare MRC with selection combining, we have to increase the number of receivers to 4 which will result into a difference of 2.5 dB in SNR. This difference widens if we further increase the number of antennas at receiver. MRC is considered better than equal gain as it differs by a gain of 0.5 dB. The output curve steeply rises initially but then becomes smooth. It might be because if we go on increasing the number of receiver antennas the complexities in obtaining the desired signal will also increase.

Acknowledgement

The authors are very much thankful to the potential reviewers for their critical comments and suggestions to improve the quality of the manuscript.