Performance Comparison of Various Robust Data Clustering Algorithms

Published Online June 2013 in MECS

Data Mining comprises of dependency detection, class identification, class description, and outlier/exception identification. The last focuses on a very small percentage of data points, which are often ignored as noise. Cluster analysis plays an important role in many engineering areas such as data analysis, image analysis and pattern recognition. Clustering helps in finding natural boundaries in the data and fuzzy clustering and is used to handle the problem of vague boundaries of clusters. In fuzzy clustering, the requirement of crisp partition of the data is replaced by a weaker requirement of fuzzy partition, where the association among data is represented by fuzzy relations. Outlier identification and clustering are interrelated processes. The fuzzy clustering identifies groups of similar data, whereas the outlier identification extracts noise from the data which does not belong to any cluster. Most analytical fuzzy clustering approaches have been deduced from Bezdek’s Fuzzy C-Means Algorithm [1]. The FCM algorithm and other algorithms derived from it have been successfully implemented in many application areas stated above aiming at reduced effect of outliers. Outlier is defined as an observation that deviates so much from other observations as to arouse suspicion that it was generated by a different mechanism. An outlying observation (or outlier) is one that appears to deviate markedly from other members of the sample in which it occurs. Outlier identification is referred to as outlier mining, which has a lot of practical applications. Outlier mining actually consists of two sub-problems: first, what data is deemed to be exceptional in a given data-set and second, find an efficient algorithm to obtain such data.

The organization of the paper is as follows: In Section II, we briefly review the conventional and robust fuzzy clustering techniques. Section III lists five properties on the basis of which the robustness of any algorithm is defined. Section IV lists various datasets that are used in this paper for experiments. Section V and VI consists of comparison of various algorithms for different datasets whereas in Section VII, we finally summarize the strength of different algorithms for various properties of robustness and Section VIII gives the final conclusion of this research.

• II.    Previous Work

• 2.1    The Fuzzy C- Means Algorithm (FCM)

This section briefly discusses the classical Fuzzy C-Means (FCM) clustering algorithm, one of the most popular clustering algorithm, and its variants. In this paper, the data-set is denoted by X, where X={x 1 , x 2 , x 3 , …… x n }, specify ‘n’ points in M-dimensional space. Centroids of clusters ‘k’ are denoted by v k , d ik is the distance between x i and v k , and ‘c’ is the number of clusters present in the data-set.

FCM [1] is the most popular fuzzy clustering algorithm. FCM algorithm defines membership of a data point into a cluster on the basis of the point’s distance from the centroid. It assumes the number of clusters as ‘c’ and minimizes the objective function:

cn

JFCM(U,V) = EE ukidki , к=1 ' =1                                      (1)

• d. = x — v.

Where ki     i k and uki is the membership of xi in cluster ‘k’, It should satisfy following condition:

c

E u« =1; ' = u,n

• ^k = 1                                                      (2)

• 2.2    Possibilistic C-Means Clustering (PCM):

Minimization of JFCM is performed by a fixed point iteration scheme known as the alternating optimization technique. It is unable to detect outliers and its centroid attraction is towards outliers rather than at the centre of the cluster.

• ZE U = 1; i = 1,2, n

• 2.3    Possibilistic Fuzzy C-Means clustering (PFCM):

constraint k=1                        and proposed a possibilistic approach to clustering by minimizing objective function as:

cn

J PCM (U, V )=EZ u"d к=1 i=1

+ E Пк E (1—U^

^k = 1      ' = 1                                 (3)

where ηk are suitable positive numbers. The first term tries to reduce the distance from data points to the centroids as low as possible and second term forces uki to be as large as possible, thus avoiding the trivial solution. This algorithm sometimes results in overlapping or identical clusters.

• N. R. Pal [3] integrated the fuzzy approach with the possibilistic approach and hence, it has two types of memberships, viz. a possibilistic (t ki ) membership that measures the absolute degree of typicality of a point in any particular cluster and a fuzzy membership (u ki ) that measures the relative degree of sharing of point among the clusters. PFCM minimizes the objective function as:

cn

JPFCM (u, V, T) = E E (aUti + btti rki + k=1 i=1

ZE Yk ZE (1—tki) k=1     i =1                           (4)

subject to the constraint that

c

E uki=1v i k=1                                                   (5)

Where, 0 “ uki, tki < 1

Here, a>0, b>0, m>1, and η>1. The constants ‘a’ and ‘b’ define the relative importance of fuzzy membership and typicality values in the objective function. Although PFCM performs better than FCM and PCM but when two highly unequal sized clusters with outliers are given, it fails to give desired results.

• 2.4    Noise Clustering (NC):

Noise clustering was introduced by Dave [4],[5] as a solution of the problem of “noise insensitivity” faced by the prior algorithms like FCM. The NC algorithm considers the outliers/noise as a separate class. It puts all the noisy elements in a separate class/cluster of outliers. The membership u*i of xi in a noise cluster is defined as

• ∗ =1-∑                         (6)

• 2.5    Credibilistic Fuzzy C-Means (CFCM):

NC reformulates FCM objective function as:

c + 1 N

J(U, V) = ZZ(u.,)m(d )2

^k = 1 ' = 1                                            (7)

Where ‘c+1’ consists of ‘c’ good clusters and one noise cluster.

Noise clustering is a better approach than FCM, PCM, and PFCM. Although, it identifies outliers in a separate cluster but does not result into efficient clusters because it fails to identify those outliers which are located in between the regular clusters (refer Section 6-Square Dataset). Its main objective is to reduce the influence of outliers on the clusters rather than identifying it.

Krishna K. Chintalapudi [6] proposed Credibilistic Fuzzy C-means (CFCM) to reduce the effect of outliers by introducing a new variable, credibility. Credibility is a function that assumes low value for outliers and high for non-outliers. CFCM defines credibility as:

ѱк=1- (1 8)- , 0≤β≤1 (8) maxj=1․․ (aj ), β ( )

Where «к ⁼ … ⁽ ^tk )

α k is the distance of vector x k from its nearest centroid. The farther x_k is from its nearest centroid, the lower is its credibility.

Since for outliers, credibility is very small so the memberships generated by CFCM for outliers are smaller than those generated with FCM. Although, it is superior to FCM, PCM, and PFCM but we observed that most of the time it assigns some outlier points to more than one cluster. Moreover, it does not separate outliers so accurate clusters are not obtained. Its main emphasis is only to reduce the effect of outliers on regular clusters.

• 2.6    Density Oriented Fuzzy C Means (DOFCM):

Like NC, DOFCM [7], [8], [9] results in ‘n+1’ clusters with ‘n’ good clusters and one invalid cluster of outliers. But the difference in this case is that DOFCM removes the outlier elements before clustering, while NC makes a different cluster of outliers at the time of clustering.

DOFCM algorithm identifies outliers on the basis of “density of points” in the data-set i.e. on the basis of the number of other points in its neighbourhood. DOFCM defines density factor, called neighbourhood membership, which measures density of an object in relation to its neighbourhood. As per the technique, the neighbourhood of a given radius of each point in a dataset has to contain at least a minimum number of other points to become a good point (non-outlier).

Neighbourhood membership of a point ‘i ’ in data-set ‘X’ is defined as:

M

i

η neighborh o d

neighborh o d ^η max

Where η ^{neighborh o d} = Number of points in neighbourhood of point i .

η max =Maximum number of points neighbourhood.

DOFCM updates the membership function as the

the

in

c

0≤∑uki ≤1

• ^{k = 1}         ; i=1, 2, 3 ….n                  (10)

instead of following the conventional in FCM

c

∑uki=1

= Maxi η ^max = ^{k = 1}

• III.    Properties of Robust Clustering Techniques

Robust clustering techniques (RCT) should have following properties to become robust against noise:

Property P1 : RCT must assign lower memberships to all the outliers for all the clusters. [6]

Property P2 : Centroids generated by RCT on a noisy data-set should not deviate significantly from those generated for the corresponding noiseless set, obtained by removing the outliers. [6]

Property P3 : RCT must be independent of any number of clusters for the same data-set i.e. it should be able to identify outliers by changing the number of clusters for the same data-set. [10]

Property P4 : RCT should be independent of any amount of outliers i.e. Centroids generated by Clustering Technique should not deviate by increasing the number of outliers. [7]

Property P5: R CT should be independent of the location of outliers in the data-sets i.e. it should be able to find out outliers whether they are in between the regular clusters (within the data-set)or away from it. [7]

• IV.    Datasets Used

• 4.1    Diamond dataset

We used the following datasets to study the properties of robust clustering techniques.

This is diamond dataset which has two clusters of 5 points and 6 points respectively and 1 outlier. We would apply FCM, PCM, PFCM, CFCM, NC and DOFCM algorithms to this dataset.

• 0к •         •         •         •         •         •         • J

  -1

  -2

  -3

  -4

• -6          -4          -2           0           2           4           6

• 4.2    Square Dataset

• 4.3    Bensaid Dataset

Fig. 1: Diamond Dataset

This is square dataset with 142 data points over two square shaped clusters, one big and one small. Bigger cluster has 81 and smaller cluster has 36 data items. It consists of 25 outliers. We would apply FCM, PCM, PFCM, CFCM, NC and DOFCM algorithms to this dataset.

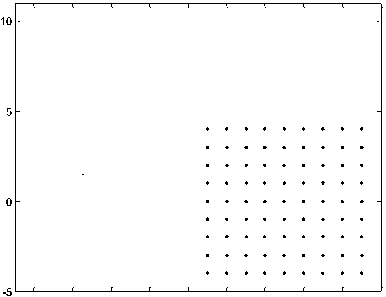
4     6     8     10     12     14    16     18    20    22

Fig. 2: Square Dataset

Bensaid is a 2-D dataset with 213 data points. It has 2 small and 1 big clusters with 18,141 and 20 data points in each data clusters. It has 34 outliers spread uniformly along the data.

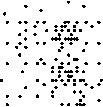
0         20        40        60        80        100        120

Fig. 3: Bensaid Dataset

• 4.4    Synthetic Dataset

This is D115 dataset where we have 115 data points clustered into two clusters of 53 and 52 items along with 10 outliers. We would apply FCM, PCM, PFCM, CFCM, NC and DOFCM algorithms to this dataset.

Fig. 4: Synthetic Dataset

• V.    Comparison of Various Algorithms on Different Datasets

  • 5.1    Diamond Dataset at a Glance

Data-set: D11, D^A12 (referred from [3]). D11 is a noiseless data-set of points [xj ^ _г . D A 12 is the union of D11 and an outlier x12.

Algorithms: FCM, PCM, PFCM, NC, CFCM, and DOFCM

Number of Clusters: 2 (Identical data with Noise)

Size of Clusters: 5, 6

Number of outliers: 1

• Figure 5 shows clustering results and outlier identification with FCM, PCM, PFCM, CFCM, NC for λ =0.6, and DOFCM for α =0. ‘*’ symbol shows

centroids and ‘o’ shows outliers identified by algorithms. So NC and DOFCM satisfy the robust clustering property P1 that outliers must have low membership values. PCM results into identical clusters. CFCM assigns one outlier point to both the clusters.

Although CFCM, NC, and DOFCM exhibit no attraction towards outliers but compare to NC, more accurate centroids are generated with DOFCM and CFCM, which corresponds to the robust clustering property P2. Performance of CFCM and NC is highly degraded by increasing the number of outliers, whereas the output of DOFCM is not affected by increasing the number of outliers and the centroids generated with DA12 are same as generated with the data-set with increased outliers which corresponds to robust clustering property P4 so it is clear that the performance of DOFCM is independent of any amount of outliers.

Clearly from Figure 5 we observed that DOFCM method can produce more accurate centroids than other methods, resulting into original clusters, and is highly robust against noise.

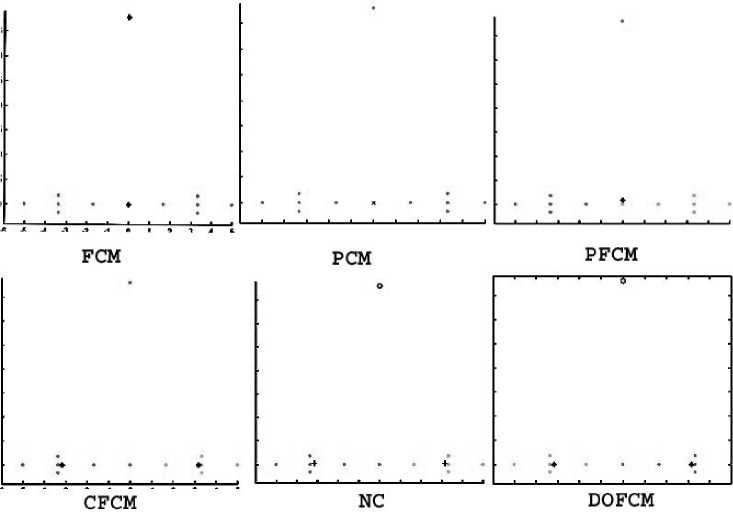
Fig. 5: Performance of different algorithms with Diamond Dataset

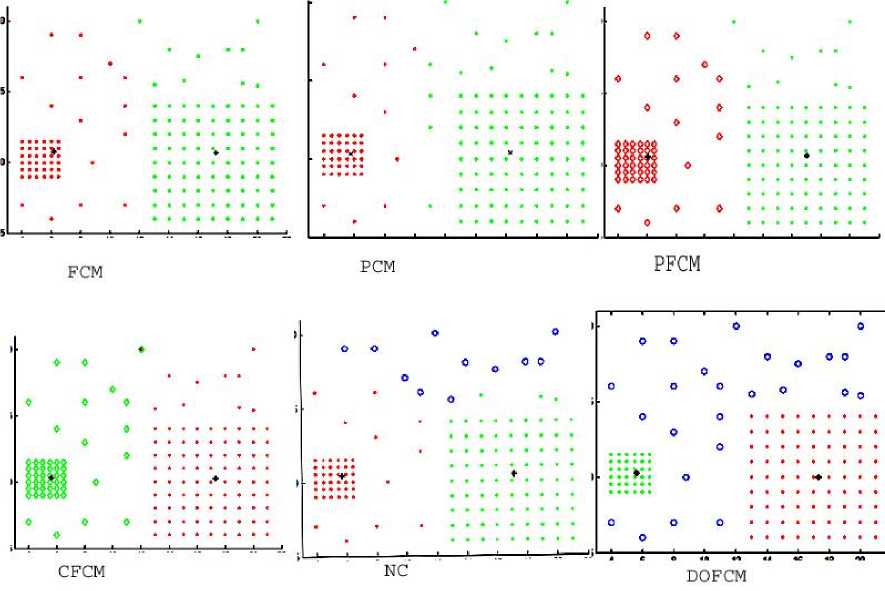
Fig. 6: Performance of different algorithms with DUNN Square Dataset

• 5.2    Square Dataset at a Glance

• 5.3    Bensaid Dataset at a Glance

Data-set: 2-dimentional Square data [11] (142 points)

Algorithm: FCM, PCM, PFCM, CFCM, NC, and DOFCM

Number of Clusters: 2

Size of Clusters: 36, 81

Number of outliers: 25

Data-set: BENSAID [12] 2-dimentional data (213 points).

Algorithm: FCM, PCM, PFCM, CFCM, NC, and DOFCM

Number of Clusters: 3 clusters with 2 small and 1 big size clusters.

Size of Clusters: 18, 141, 20

Number of outliers: 34

BENSAID’s two-dimensional data-set consisting of one big and two small size clusters is used in this example. We have saved the structure of this set but have increased count of core points and added uniform noise to it, which is distributed over the region [0,120] x [10,80]. Figure 7 shows clustering result of FCM, PCM, PFCM, CFCM, NC with λ =0.17, and DOFCM with α =0.

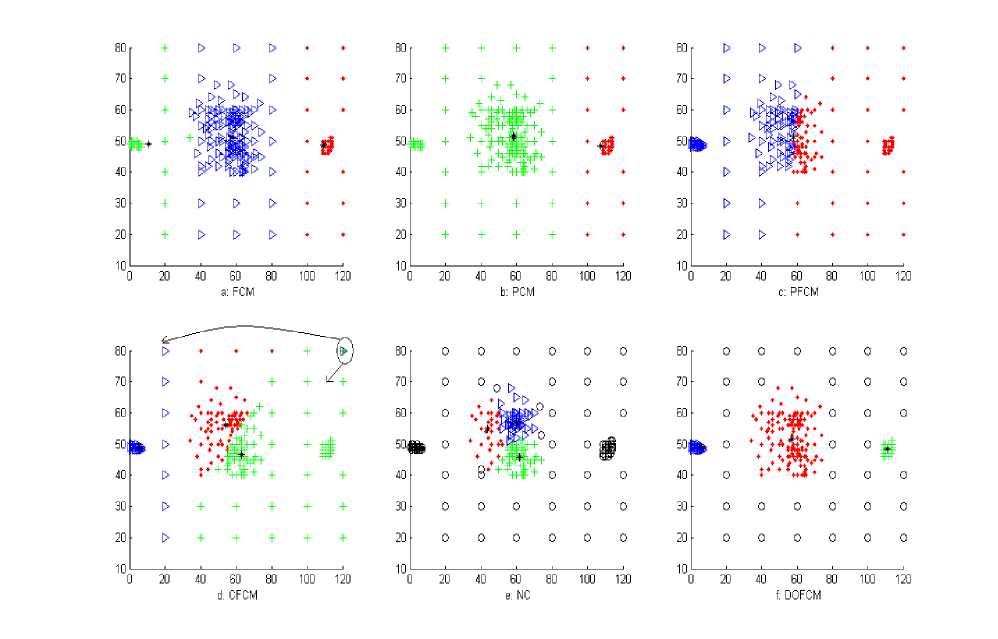
Fig. 7: Performance of different algorithms with Bensaid's Dataset

All the three clusters in the Figure are separated with the symbols ‘.’, ‘+’, and ‘▷’. Centroids of the clusters are plotted with ‘*’and outliers are plotted with ‘o’. We observed that performance of FCM is highly affected by outliers. PCM is unable to detect unequal size clusters so could detect only two clusters. PFCM results into two overlapping clusters. CFCM detected three clusters but not the correct ones and also assigned one outlier point to two clusters. From Figure, we observed that NC fails to detect small clusters and considered them as outliers. It partitioned the bigger cluster into three parts. It is evident from the Fig that DOFCM has identified all the outliers and is able to detect original clusters from noisy data-set.

• 5.4    Synthetic Data Set at a Glance

Data-set: D115 (data-set containing 115 points)

Algorithm: FCM, PCM, PFCM, CFCM, NC, and DOFCM

Number of Clusters:  2 (Two clusters of approximately equal size)

Size of Clusters: 53, 52

Number of Outliers: 10

Data-set used in this example consisting of two clusters of approximately equal size with noise and the data points are distributed over two dimensional spaces. Figure 8 shows original data-set in its noisy version. We tried various values of ‘λ’ and ‘α’. NC and DOFCM show best results with ‘λ’=0.5 and ‘α=0.14’. Figure 8 shows clustering result of FCM, PCM, PFCM, CFCM, NC, and DOFCM with two clusters. The centroids of the clusters are plotted with symbol ‘*’and outliers are plotted with ‘o’. PFCM and CFCM, although, able to reduce the effect of outliers on the centroid locations but do not result into accurate clusters because outliers are included in their final clusters. Moreover, CFCM assigned some outlier points to more than one cluster. NC identified outliers with two clusters but when the number of clusters is increased to four, it did not identify outliers because by increasing the number of clusters, the average distance of points from the cluster centroids decreases than their distance from noise cluster and NC consider a point to be an outlier only if its distance to noise cluster is less than the distance from regular clusters. It is visually verified that DOFCM has identified same number of outliers as required and is independent of the number of clusters because it identifies outliers based upon density of data-set which is independent of number of clusters so it also satisfies robust clustering property P3. If we compare the visual results of clustering with the original data-set as shown in Figure 4, DOFCM results into original clusters.

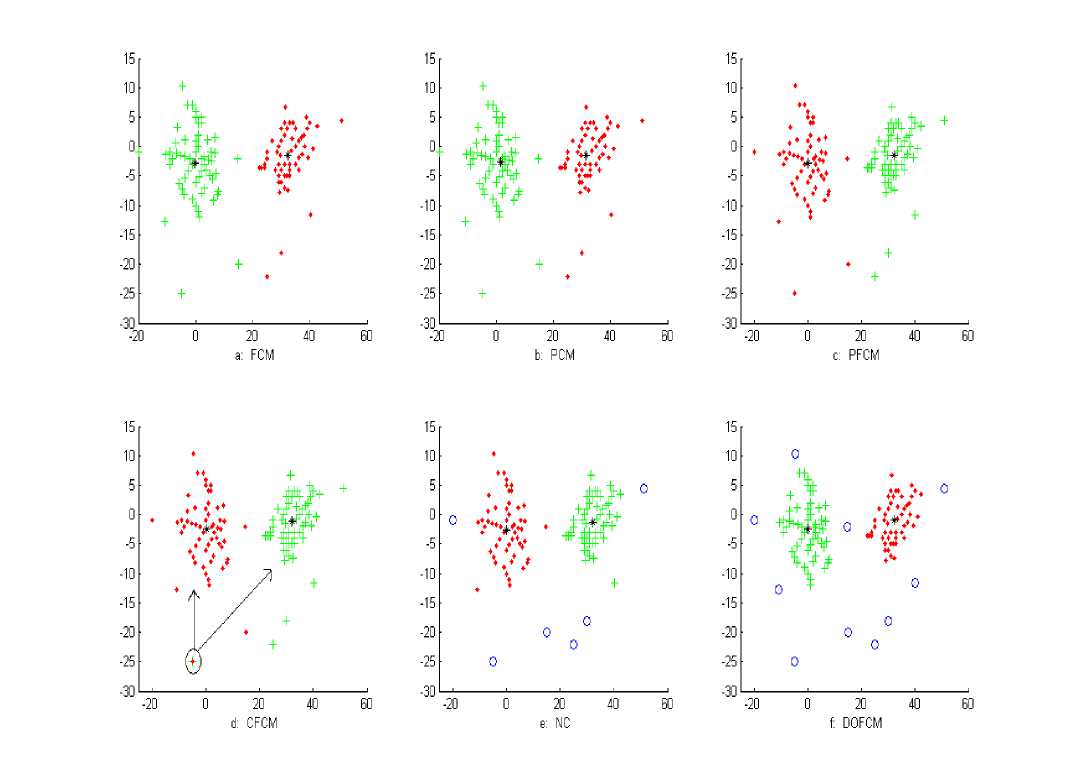
Fig. 8: Performance of different algorithms with Synthetic Dataset

• VI.    Comparison of Values for Various Algorithms in Different Datasets

This section gives us a tabular overview of six fuzzy clustering techniques for their generated centroid locations (cx, cy) and execution time for four different datasets used. For FCM algorithm applied to diamond dataset, Cx represents value of ‘x’ coordinates and Cy would represent value of ‘y’ coordinates for the two clusters generated. However, in case of NC, the algorithm generates ‘c+1’ clusters where ‘c’ clusters are good which in this case are 2 and one cluster define the outliers/noise identified.

Table 1: Comparison for Different Datasets for Considered Algorithms

DATASET	TECHNIQUE /ALGORITHM USED	No. of clusters	Cx	Cy	Execution Time
DIAMOND DATASET	FCM	2	[2.68e-06;-3.44e-07]	[-0.0010;37.96]	0.0195
	PCM	2	[1.9647e-005;-1.9957e-005]	[0.013351;0.013387]	0.063
	PFCM	2	[-7.4531e-04;7.4531e-04]	[0.8198;0.8198]
	CFCM	2	[-3.1796;3.1796]	[-2.4134e-11;3.4680e-11]	0.156
	NC	3	[3.1529;-3.1529]	[0.2067;0.2067]	0.0205
	DOFCM	2	[3.1672;-3.1674]	[-1.2554e-07; 1.2819e-07]	0.0088
DIAMOND DATASET WITH ADDED OUTLIERS	FCM	2	[-6.7901e-10;2.4754e-11]	[-6.1049e-04;35.7590]	0.0169
	PCM	2	[-1.0986e-020;5.37e-008]	[36.884;0.0036092]	0.047
	PFCM	2	[5.8412e-08;-1.5004e-10]	[5.8055e-04;36.0390
	CFCM	2	[3.1737;-3.1737]	[0.0577;0.0577]	0.0146
	NC	3	[3.0927;-3.0927]	[0.7155;0.7157]	0.0245
	DOFCM	2	[-3.1672;3.1674]	[5.8361e-08;-5.9898e-08]	0.0097
SQUARE DATASET	FCM	2	[17.2073;6.1827]	[0.7046;0.7821]	0.019
	PCM	2	[5.78;16.242;]	[0.30072;0.38665]	0.031
	PFCM	2	[6.0124;17.0326]	[0.6071;0.6620]
	CFCM	2	[5.5927;17.3011]	[0.2987;0.2857]	0.0126
	NC	3	[5.7178;17.1290]	[0.4027;0.4533]	0.0274
	DOFCM	2	[4.6842;5.8157]	[0.1350;0.6351]	0.0187
BENSAID'S DATA	FCM	3	[1.0921e+02;57.7515;10.6430]	[48.6981;51.4926;49.1197]	0.0188
	PCM	3	[107.38;58.269;58.671]	[48.55;51.414;51.367]	0.047
	PFCM	3	[58.04;58.04;58.04]	[51.25;51.25;51.25]
	CFCM	3	[63.18;5.60;53.51]	[46.82;48.80;55.99]	0.02
	NC	4	[62.0950;60.0808;42.7174]	[45.4450;56.6894;54.3447]	0.0274
	DOFCM	3	[5.53036;57.3060;1.1082e+02]	[49.0016;51.5007;48.4870]	0.0254
SYNTHETIC DATA(d115)	FCM	2	[-0.26106;32.391]	[-2.8041;-1.5826]	0.031
	PCM	2	[32.235;0.061313]	[-2.6137;-1.4948]	0.047
	PFCM	2	[32.235;0.061313]	[-1.5342;-2.7499]
	CFCM	2	[32.267;0.34857]	[-1.1779;-2.4388]	0.015
	NC	3	[32.252;0.15301]	[-1.3224;-2.5565]	0.033
	DOFCM	2	[3.7382;32.122;-3.4128]	[-4.1914;-1.1842;-0.92712]	0.031

Table 2: Efficiency of Algorithms

		FCM	PCM	PFCM	CFCM	NC	DOFCM
	PROPERTY
P1	ASSIGN LOWER MEMBERSHIP TO OUTLIERS	NO	NO	NO	YES	YES	YES
P2	CENTROID NOT DEVIATE ON ADDING OUTLIERS	NO	NO	YES	YES	YES	YES
P3	INDEPENDENT OF NUMBER OF CLUSTERS	NO	NO	NO	NO	NO	YES
P4	INDEPENDENT OF NUMBER OF OUTLIERS	NO	NO	NO	YES	YES	YES
P5	INDEPENDENT OF LOCATION OF OUTLIERS	NO	NO	NO	NO	NO	YES

• VII.    Efficiency of Algorithms on Basis of Five Clustering Properties

This section gives us a tabular representation of how effective each algorithm is on the basis of the five properties mentioned in Section III.

• VIII.    Conclusion

Density-oriented Fuzzy C-means algorithm, which identifies outliers before clustering process, results into original clusters. In comparison to FCM, PCM, PFCM, CFCM, and NC Density Oriented Clustering method identifies outliers very well and select more desirable cluster centroids, thereby, increasing the clustering accuracy. It has been found on applying these algorithms to different datasets that DOFCM algorithm is highly robust to noise and outliers, detects original clusters from noisy data-set. But its degree of robustness would rely on the value of α which has to be chosen carefully.

Conference of Fuzzy sets and Systems, Korea, August 20-24, pp. 373-378.

• [9]    Kaur Prabhjot, Anjana Gosain, “Density-Oriented Approach to Identify Outliers and Get Noiseless Clusters in Fuzzy C – Means ”, 2010 IEEE

Conference of Fuzzy sets and Systems, Korea, Barcelona, Spain.

• [10]    Rehm F., F. Klawonn, and R. Kruse (2007), “A Novel Approach to Noise Clustering for Outlier Detection”, Applications and Science in Soft Computing, Springer-Verlag 11:489-494.

• [11]    Dunn, J., 1974. A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters. J. Cybernet. 3, 32–57.

• [12]    Bensaid A. M., L.O. hall, J. C. Bezdek, L. P. Clarke, M. L. Silbiger, J. A. Arrington, R. F. Murtagh, “Validity-guided clustering with applications to image segmentation”, IEEE trans. Fuzzy Systems 4 (2) (1996) 112-123.

• [1]    Bezdek J. C., Pattern Recognition with Fuzzy Pointive Function Algorithm, Plenum, NY, 1981.

• [2]    Krishnapuram R. and J. Keller, "A Possibilistic Approach to Clustering", IEEE Trans. on Fuzzy Systems, vol .1. No.2,pp. 98-110, 1993.

• [3]    Pal N.R., K. Pal, J. Keller and J. C. Bezdek ," A Possibilistic Fuzzy c- Means Clustering Algorithm", IEEE Trans. on Fuzzy Systems, vol 13 (4),pp 517-530,2005.

• [4]    Dave R. N., “Characterization and detection of noise in clustering”, Pattern Rec. Letters, vol. 12(11), pp 657-664, 1991.

• [5]    Dave R. N., “Robust fuzzy clustering algorithms,” in 2^nd IEEE Int. Conf. Fuzzy Systems, San Francisco, CA, Mar. 28-Apr. 1, 1993, pp. 12811286.

• [6]    Chintalapudi K. K. and M. kam, “A noise resistant fuzzy c-means algorithm for clustering,” IEEE conference on Fuzzy Systems Proceedings, vol. 2, May 1998, pp. 1458-1463.

• [7]    Kaur, P., Gosain, A. (2011), “A Density Oriented Fuzzy C-Means Clustering Algorithm for Recognizing Original Cluster Shapes from Noisy Data” International Journal of      Innovative

Computing    and    Applications    (IJICA),

INDERSCIENCE ENTERPRISES, Vol. 3, No. 2, pp.77–87.

• [8]    Kaur Prabhjot, Anjana Gosain, “Improving the performance of Fuzzy Clustering Algorithms through Outlier Identification”, 2009 IEEE

  Prabhjot Kaur has completed her B. Tech. in 1999 and M. Tech. in 2003. Presently she is working as a Reader in Maharaja Surajmal Institute of Technology and pursuing her P.hD. from Sharda University, Greater Noida, New Delhi. Her area of interest includes Soft computing, Image processing, Medical Image segmentation.