Performance estimation of differential evolution, particle swarm optimization and cuckoo search algorithms

Published Online June 2018 in MECS

Optimization is a branch of science in which the best values of parameters of the problems are discovered up to certain limitations. There are various optimization procedures available in the literature. Optimization problems can be classified like Linear programming, Integer programming, Combinatorial optimization and Metaheuristic optimization [1] [2]. Linear programming and Integer programming methods could not find global optimum solutions for a non-deterministic polynomial time (NP)-hard problems with large numbers of variables and non-linear objective functions [3]. Metaheuristic algorithms are stochastic search procedures which mimic the natural biological advancement and/or the social manners. Metaheuristic optimization algorithms find optimum solution of an objective function using global exploration and local exploitation. The performance of various optimization algorithms can be estimated using various unimodal and multimodal benchmark functions. Many metaheuristic optimization algorithms have been developed in last few years. As per No Free Lunch (NFL) theorem, no single algorithm is best suited to solve all optimization problems [4]. So this paper depicts the hybrid algorithm concept for maximizing the performance by collaborating different metaheuristic algorithm.

• II.    Related works

Genetic Algorithm (GA) developed by Holland is the most popular and oldest optimization algorithm [5] [6]. Reference [7] describes basics of Particle Swarm Optimization (PSO) algorithm proposed by J. Kennedy and R. Eberhart. PSO algorithm has good local exploitation. Ant Colony Optimization (ACO) algorithm has been inspired by the foraging behavior of real ants [8]. The Differential Evolution (DE) algorithm developed by Kenneth Price and Rainer Storn is a population-based stochastic method for global optimization [9]. Artificial Bee Colony (ABC) algorithm proposed by Dervis Karaboga is motivated by the intelligent behavior of honey bees [10]. Cuckoo Search (CS) algorithm is the latest metaheuristic algorithm proposed by Yang and Deb [11]. The CS algorithm has a better explorative capability. Metaheuristic algorithms developed in recent years by many researchers are Firefly Algorithm (FA) [12] [13], Bat algorithm [14] [15], Stochastic Fractal Search (SFS) [16], Wind Driven Algorithm (WDA) [17], Grey Wolf Optimizer (GWO) [18], Symbiotic Organisms Search

• (SOS)    [19] and Grass Fibrous Root Optimization Algorithm (GRA) [20]. A comparison of GA, ACO, Reverse Formation Dynamics (RFD), FA and CS algorithm for Traveling Sales Man problem had been studied in [21]. In this work, the performance of PSO, DE, CS and hybrid algorithm of CS and PSO (CSPSO) is evaluated using 11 standard benchmark functions.

The content of this paper is structured as follows. The PSO, DE and CS algorithms are briefly described in section III. The concept of hybrid CSPSO algorithm is represented in section IV. The various standard benchmark functions used for the testing purpose are presented in section V. Experimental settings and simulation results are presented in section VI. Conclusions are discussed in section VII.

• III.    DE, PSO and CS Algorithms

• A.    Differential Evolution Algorithm

The DE algorithm uses the mutation, crossover, and selection strategies of GA. There are many mutation techniques for DE algorithm given in literature [9] [22]. The DE/rand/1/bin is the most commonly used technique to search the global optimum [22]. DE algorithm consist of two arrays, each one holding population size N and dimension D. The first array holds the current vector population, while the second array holds vector population for the next generation. In each generation, N competitions are carried out to get the resultant composition of the consecutive generation. The vector differential (X_r0 – X_r1) is defined by a pair of vectors X_r0 and X_r1. Both vectors X_r0 and X_r1 are chosen at random, and their weighted difference is multiplied by some weighted factor which is further added to another randomly chosen vector X r2 . This process can be mathematically represented using following equation.

X = X r 2 + F *( X r 0 - X r 1 )            (1)

The weighting factor F is a constant supplied by the user in the optimal range of (0.5, 1) [22]. In DE algorithm main control parameters are F, N and crossover rate (CR) [22]. The main steps of DE algorithm are given by the flow diagram in Fig. 1.

• B.    Particle Swarm Optimization Algorithm

The PSO algorithm is basically a swarm intelligent based evolutionary algorithm [7]. It finds the best optimal result using a set of flying birds with different velocities. The velocities of these birds are dynamically adjusted based on their past performance, as well as their neighbor in the exploration space. In this algorithm, each solution bird in folk is known as a particle. The birds in the population change their social performance based on their movement toward the destination. This algorithm works in an iteration manner and finds the best solution. The main steps for PSO algorithm are given by the flow diagram as shown in Fig. 2.

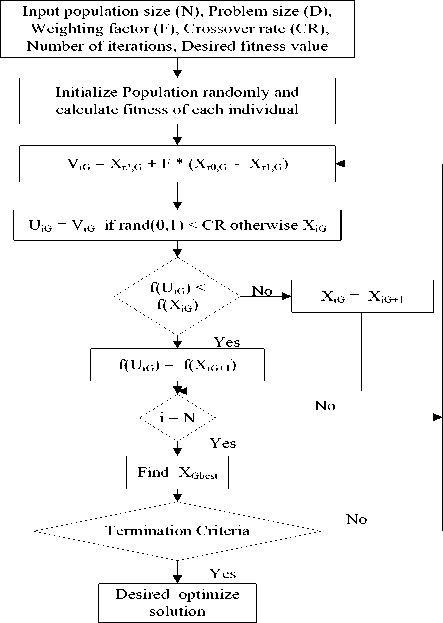
Fig.1. Flowchart of DE Algorithm.

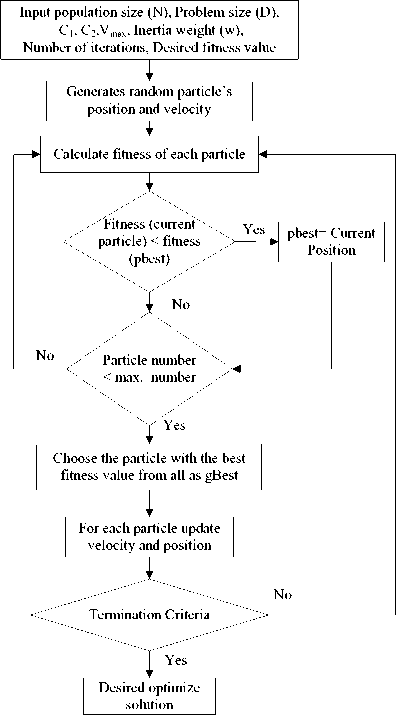
Fig.2. Flowchart of PSO Algorithm

Suppose particle swam consists of N number of particles with D dimension. The position and velocity of the k^th particle are characterized by X k = [X k ¹, X k ², . . .,X k ^D] and V k = [V k ¹, V k ²,. . .,V k ^D]. The velocity of the k^th particle after each iteration is updated according to the equation given below [13].

V= W * Vd+Cl* randl * (pbestd - X.) + C2* rand2*(gbest - Xkd)

Here, the range of k is {1, 2, 3........., N}, the range of d is {1, 2, 3…., D}, the range of i is {1, 2, 3.... maximum iteration number}, pbest is particle’s personal current best position, gbest is particle’s global best position, rand1 and rand2 are uniformly distributed random numbers between 0 and 1, C1 and C2 are constants known as acceleration coefficients, W is known as inertia weight which is initially chosen less than one and then reduced linearly with each iteration. W controls the influence of the previous direction of displacement. The position of the kth particle in N x D dimension of the search space can be calculated using the following equation.

XD = XV + VD1          (3)

Input number of nest (N), Problem Size (D), Fraction of worst nest (p a ) ,Number of iterations, Desired fitness value

______________i______________

Generate initial population of N nest and find current best solution

______________i______________

Generate Cuckoo by random Lévy walk

______________i______________

Evaluate Fitness of each Cuckoo

Replace better quality Cuckoo to nest

Abandon a fraction of worse nests (p a ), and build new one at new location via random walk

Choose the nest with the best fitness value from all as gBest

No

Yes

Desired optimize solution

• C.    Cuckoo Search Algorithm

The CS algorithm developed by Xin-She Yang and Suash Deb is a population-based stochastic global search algorithm [11]. This algorithm is motivated by the exceptional lifestyle of the cuckoo species. The main steps of CS algorithm are given by the flow diagram in Fig. 3. In this algorithm, each pattern relates to a nest and each individual element of the pattern relates to a Cuckoo egg [11]. The common process equation of the CS algorithm is represented by following equation [11].

X g + 1;, = X g ;1 + a ® Livy ( 2 ) (4)

Here, α > 0 is the step size which depends on scales of the problem of interests and g represents the number of the current generation. The product ⊗ indicates the entrywise multiplication. Lévy (λ) is random walk using Lévy flight which is more effective in the long run as compared to a random walk in PSO algorithm. Lévy (λ) is derived from a Lévy distribution with an infinite variance and infinite mean [11].

Levy ~ u = t ^-2 (5)

Here, step size follows random walk process with a power law distribution with heavy-tailed. CS is a population-based stochastic optimization algorithm similar to DE and PSO algorithms, but it uses some sort of elitism and/or selection similar to that used in harmony search [11]. The randomization is more efficient in CS algorithm as compared to PSO and DE algorithms [11]. CS algorithm requires fewer parameters to be adjusted as compared to DE and PSO algorithms [11].

• IV.    Hybrid CSPSO Algorithm

In this section, a hybrid algorithm of CS and PSO algorithms is presented. The main steps of the hybrid CSPSO algorithm are given by the flow diagram in Fig. 4. PSO is one of the most capable optimization algorithms, but it converges rapidly so it has premature convergence generally in complex problems [23].

The CS algorithm is used to solve a number of complex problems and outperformed other algorithms [24]. CS algorithm may converge marginally slower but it has better explorative skill. There is no algorithm that can efficiently optimize all optimization problems. To resolve this issue, merging of the current algorithms can be done to find the global optimum solution [25]. The convergence rate and global search ability can be improved using the hybrid algorithm. It can decrease the possibility of being stuck in local minima. The hybrid algorithm can be designed to make the best use of best features of both algorithms.

Fig.3. Flowchart of CS Algorithm

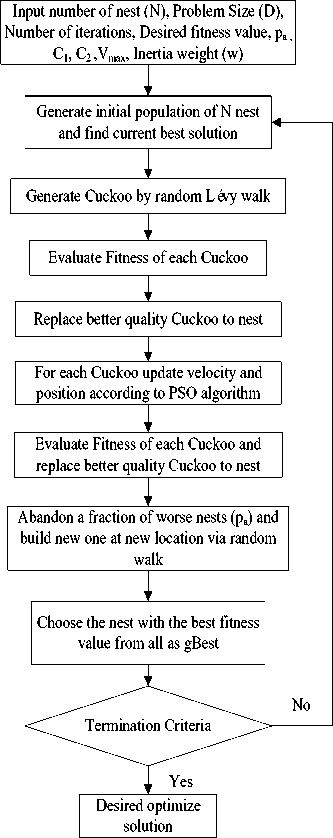
Fig.4. Flowchart of CSPSO Algorithm

• V.    benchmrk Functions

Performance of an optimization algorithm can be estimated using typical standard benchmark functions [26]. There are different types of such test functions are represented in the literature. Some of the benchmark functions we have been used for performance evaluation of DE, PSO, CS and hybrid CSPSO algorithms. The benchmark functions used in this work are listed in Table 1 with their search space, dimension and desired fitness value.

• VI.    Experemintalsettings and results

All these algorithms were implemented using C language and tested on a system consisting of core i5, 2.4 GHz processor with 8 GB internal RAM and Ubuntu as an operating system. Every algorithm has its own parameters which vary its performance in terms of solution quality and processing time.

In DE algorithm, control variables setting of F, CR and N can be quite difficult and some benchmark functions are very sensitive to proper settings these control variables [22]. For this work, N = 10*D, F = 0.8 and CR = 0.5 are chosen for DE algorithm [22]. In PSO algorithm, we have used N = 30, C 1 = 1.47, C 2 = 1.47, V max = X max , V min = X min and W = [0.4, 0.9] [27]. CS algorithm requires less parameters as compared to DE and PSO algorithms. In CS algorithm, N = 30 and p_a = 0.25 are chosen [11]. In hybrid CSPSO algorithm, N = 30, C 1 = 1.47, C 2 = 1.47, V max = X max , V min = X min , W = [0.4, 0.9] and p a = 0.25 are chosen.

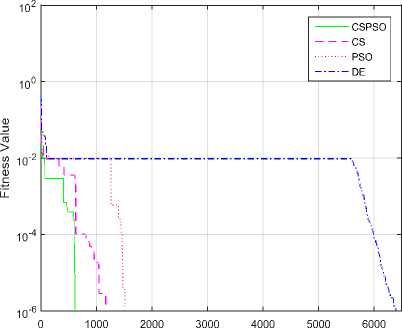
The convergence graphs optimized by DE, PSO, CS and CSPSO algorithms of different benchmark functions are listed in Table 1 as shown in Fig. 5 to Fig. 15. The vertical axis is fitness value and the horizontal axis is the number of iterations. From Fig. 5 to Fig. 15, we can observe that the CS algorithm requires fewer iterations as compared to those in PSO algorithm to reach required fitness values for all benchmark functions. The CS algorithm also requires fewer iterations as compared to those in DE algorithm to reach required fitness values for all benchmark functions except in Rastrigin function. The convergence graphs also show that CSPSO algorithm outperforms DE, PSO and CS algorithms for almost all benchmark functions.

Table 1. Standard Benchmark Functions

Function	Dimension D	Type	Search Space	Fitness Value
Ackley	8	Multimodal	(-32, 32)	10 -6
Beale	2	Unimodal	(-4.5, 4.5)	10-6
Bukin	2	Multimodal	-15<< X < -5 -3 < X < 3	10-6
Easom	2	Unimodal	(-100, 100)	-1
Griewank	8	Multimodal	(-600, 600)	10-6
Lévy	8	Multimodal	(-10, 10)	10 -6
Michalewicz	10	Multimodal	(0, п)	-9.66
Rastrigrin	8	Multimodal	(-5.12, 5.12)	10 -6
Rosenbrock	8	Unimodal	(-30, 30)	10-6
Schaffer	2	Multimodal	(-100, 100)	10 -6
Sphere	8	Unimodal	(-100, 100)	10 -6

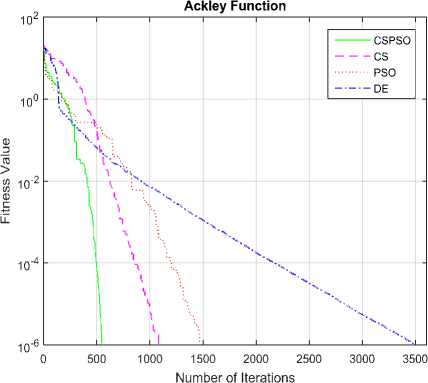
Fig.5. Convergence graph of DE, PSO, CS and CSPSO algorithms for Ackley function

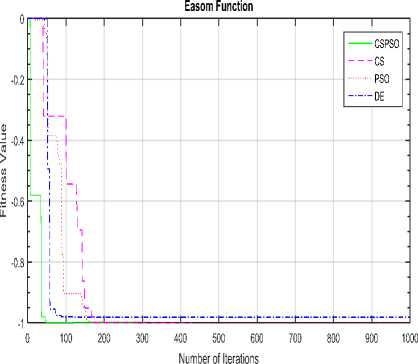
Fig.8. Convergence graph of DE, PSO, CS and CSPSO algorithms for Easom function

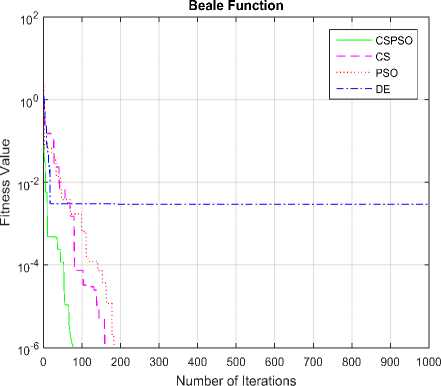
Fig.6. Convergence graph of DE, PSO, CS and CSPSO algorithms for Beale function

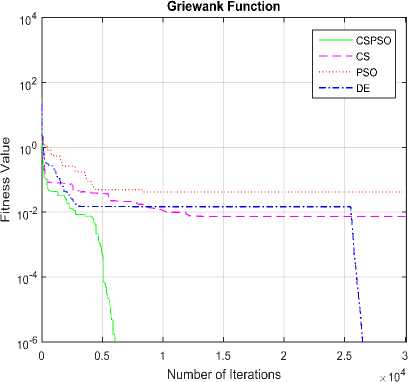
Fig.9. Convergence graph of DE, PSO, CS and CSPSO algorithms for Griewank function

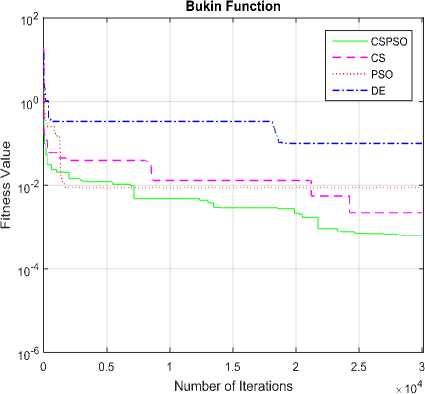
Fig.7. Convergence graph of DE, PSO, CS and CSPSO algorithms for Bukin function

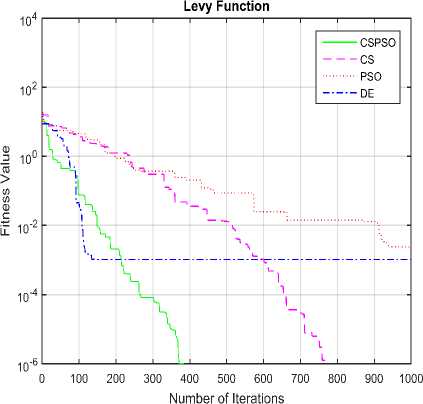
Fig.10. Convergence graph of DE, PSO, CS and CSPSO algorithms for Lévy function

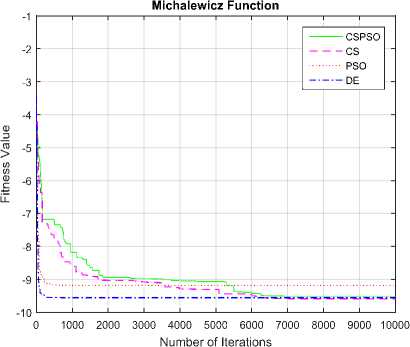
Fig.11. Convergence graph of DE, PSO, CS and CSPSO algorithms for Michalewicz function

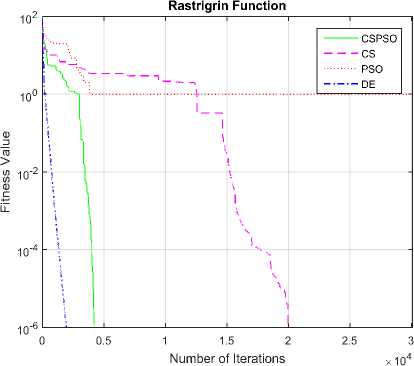
Fig.12. Convergence graph of DE, PSO, CS and CSPSO algorithms for Rastrigrin function

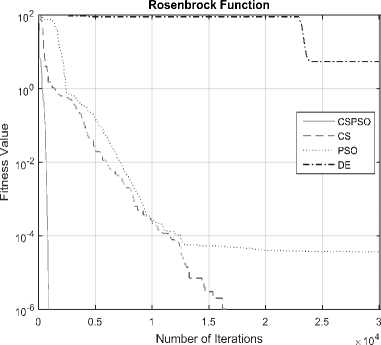
Fig.13. Convergence graph of DE, PSO, CS and CSPSO algorithms for Rosenbrock function

Each experiment is repeated for 100 independent runs with different random seeds. The standard deviation, average number of iterations and simulation time obtained by DE, PSO, CS and CSPSO algorithms are given in Table 2. From Table 2, it is observed that PSO algorithm requires less simulation time for all functions. CS and CSPSO require fewer iterations to reach required fitness value. CS and CSPSO give less standard deviation for all functions.

Schaffer Function

Number of Iterations

Fig.14. Convergence graph of DE, PSO, CS and CSPSO algorithms for Schaffer function

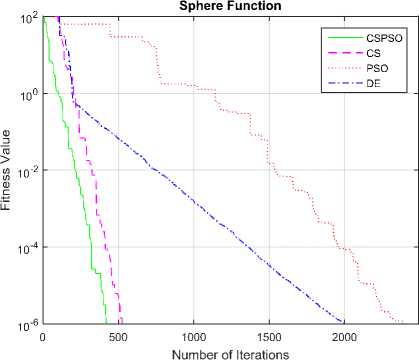
Fig.15. Convergence graph of DE, PSO, CS and CSPSO algorithms for Sphere function

• VII.    Conclusion

PSO, DE and CS algorithms are implemented using C language and tested on 11 unimodal and multimodal nonlinear benchmark functions. CS algorithm requires fewer control parameters as compared to PSO and DE algorithms. Experimental simulation results show that CS algorithm is more efficient as compared to PSO algorithm for all unimodal and multimodal functions. The CS algorithm also outperforms DE algorithm except for Rastrigrin function. PSO algorithm is most commonly used algorithm due to its easiness of implementation and fast convergence speed. In contrast, CS algorithm has good ability to find a global optimum solution. To use the advantages of CS and PSO algorithms, a hybrid algorithm of CS and PSO is implemented and tested with the same benchmark functions. The simulation results show that hybrid CSPSO algorithm outperforms PSO, DE and CS algorithms.

Table 2. Simulation Results

Algorithm	Function	Standard Deviation	Average Iterations	Simulation Time (s)
DE	Ackley	0.0	4021	28.69
PSO		0.0	1521	5.60
CS		0.0	1107	16.59
CSPSO		0.0	553	10.53
DE	Beale	0.0046	28514	42.75
PSO		0.0	580	0.83
CS		0.0	154	0.60
CSPSO		0.0	89	0.42
DE	Bukin	0.0048	30000	37.29
PSO		0.0122	30000	22.92
CS		0.0032	30000	119.20
CSPSO		0.0035	30000	137.79
DE	Easom	0.0069	30000	59.49
PSO		0.0	1051	1.45
CS		0.0	480	2.54
CSPSO		0.0	311	2.09
DE	Griewank	0.0063	20529	168,69
PSO		0.0170	29514	111.33
CS		0.0124	26530	408.61
CSPSO		0.0123	25071	471.54
DE	Lévy	0.0082	30000	294.62
PSO		0.0	2147	10.01
CS		0.0	746	12.11
CSPSO		0.0	387	8.27
DE	Michalewicz	0.1065	22261	333.86
PSO		0.4183	30000	159.79
CS		0.1163	26166	544.96
CSPSO		0.1267	26122	719.06
DE	Rastrigrin	0.0	17776	92.05
PSO		0.3233	7073	20.72
CS		0.532	10550	146.47
CSPSO		0.4532	8805	157.10
DE	Rosenbrock	19.39	30000	114.56
PSO		8954.35	29279	82.19
CS		0.0	1234	14.52
CSPSO		0.0	993	13.66
DE	Schaffer	0.0	6245	4.71
PSO		0.0	786	0.83
CS		0.0	1258	5.89
CSPSO		0.0	462	2.65
DE	Sphere	0.0	1904	6.78
PSO		0.0	2662	4.95
CS		0.0	568	6.87
CSPSO		0.0	416	5.59