Performance Study on the System of Real-Time VBR Service with Shared Cache

The limitation of the network resources and the extensive applications of compression coding technology cause the majority of services to be VBR service in integrated services digital network (ISDN). A VBR service is quite strict with the delay constraints of the cell and is suitable for the burst data applications that are sensitive to time.

At present, the performance of the real-time service system has been extensively studied. Jaramillo and Srikant made a study on the delay of ad hoc wireless networks that supported a mixture of best-effort service and real-time service and proposed a joint congestion control and scheduling algorithm [1]. However, it did

* Corresponding author.

not study other performance parameters of the system. Huang and Shi did a research on the performance of the broadband multiplex system that provided real-time VBR service and best effort service [2]. Moreover, the article arrived at a new conclusion that the packet loss rate was not a monotonic function of the call level load. Nevertheless, it did not make a study of adding up a cache in the system. Epiphaniou et al. utilized jitter, end-to-end delay and packet loss to measure the affects of different queuing mechanisms on real-time voice service [3]. However, they only did some research on single service. A performance analysis was presented for macro-diversity integrated voice/data CDMA systems. A simple birth-and-death Markov process was used to evaluate the QoS performances of resulting data users and blocking and outage probabilities were used to CAC decisions in [4]. Nevertheless, the CAC decisions did not consider the influence of packet-level performance parameters on the system. Huang and Kuo proposed a kind of CAC strategy that combined connection-level performance and packet-level performance [5]. However, the article only carried out a study on a system with single real-time VBR service and did not take into account the case with a cache. A CAC scheme was proposed in wireless cellular networks based on bandwidth degradation and queue buffers, which not only reduced handoff dropping probability and call blocking probability (CBP) but also reduced degradable frequency with a fixed degradable ratio [6]. However, it merely improved connection-level QoS, without improving packet-level QoS.

In view of the present research, this paper, under complete sharing policy, proposes a system model that has shared cache and supports many kinds of real-time VBR services. In a unit of time, with the assumption of each channel only transmitting a definite length of data packet, we obtain arrival probability distribution of the number of packets in the system. Then the packet loss rate and the delay performance of the system are analyzed by queuing theory.

The rest of the paper is organized as follows. The system model is presented and its performance is analyzed in Section II. Section III gives the numerical calculation and the performance analysis to the system. In Section IV, it proposes a joint CAC algorithm guaranteeing both packet-level QoS and connection-level QoS. Finally, Section V concludes the paper and discusses the future research directions.

• 2.    System Model and Performance Analysis

The system that this article discusses meets the following conditions: 1, it supports many kinds of real-time VBR services with different peak rates and the arrival processes of services are Poisson processes with mutually independence. 2, call admission adopts complete sharing policy. 3, each server device serves for a user at the same time and the server devices that each user needs start and finish the service simultaneously. 4, the system supports K ( K is a finite positive integer) kinds of real-time VBR services and the service time of each type of service obeys exponential distribution, of which the Laplace transform has rational expression. 5, if the system has not enough server devices, it is able to cache some of the packets with a fair discarding proportion.

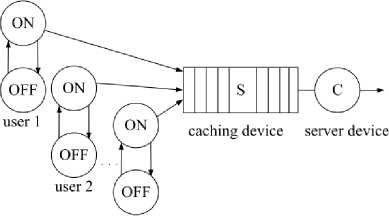
user N

The packets from different sources are mostly served based on statistical multiplexing. Therefore, the number of users is not limited to the service capacity of the system and the number of users that the system can hold can be much larger than the capacity. We term the acceptable threshold that is the allowed maximum of the sum of peak information rates of all online connections as virtual capacity. In this paper, virtual capacity and physical capacity are respectively represented by virtual channel numbers N and physical channel numbers C ( C <  N ) . The vector of online connections is defined as n = ( n 1 , — , n_K ) and we denote the parts that are temporarily in an ON state in these online connections by n ' = ( n 1 ' , — , n ' _K ). The single service with different types occupies channel numbers, which produces cells at a peak rate in an ON state. The occupied channel numbers constitute the vector b = ( b 1 , — , b_K ). The probability of the i -th service connection in an ON state is P _{on i} . Meanwhile, the arrival rate of connection request, service rate and load are separately defined as X i , p i and a i .

The probability distribution P (n) of online connections conforms to the product form under complete sharing policy and it is given by [7]

K n i

P (n) = П    (GG ( Q )),n eQ                                                           (1)

=1 ⁿ , -!

Where G ( Q ) = У | П— I , - , = — , Q = {n:0 <  n • b <  N , b i <  b , ₊₁, i = 1, — , K - 1}.

neQ ( / =rnj J       P i

• 2.1.    System Model Based on ON-OFF Type VBR Flows

• 2.2.    The Calculation of Call Blocking Probability

The statistical properties of practical VBR service flows are very often difficult to describe precisely, whereas ON-OFF model not only reflects the basic characteristics of VBR services, but also simplifies complexity of queuing analysis. However, the general ON-OFF model is only applied to the system with single type VBR service source. In fact, broadband integrated services network supports the VBR service with different statistical characteristics. Consequently, the ON-OFF model is extended and is applied to the system with many types of VBR service flows coexisting in this paper. The model is shown in Fig. 1.

When an ON-OFF information source is in an ON state, it sends data packets at a peak rate but does not send data packets in an OFF state. The number of type i VBR service sources is ni . For this type information sources, the probabilities that are in an ON and OFF state are separately defined as Poni and Poffi . Because of the independence of information sources, the probability Pi that n' of the ni service sources are in an ON state follows Bernoulli distribution

( \ n - n'

1-P I

¹ P on , )

CBP is one of the key indexes for evaluating the call-level QoS. For system with a complete sharing policy, Kaufman proposed a method of calculating CBP based on "insensitivity property" [7]. With the above as base, Awater proposed a method of calculating CBP based on the complete sharing system with various resource requirements [8]. In this paper, the calculation of CBP will be obtained by direct method.

For the system that can provide K kinds of services, the peak bandwidth of the system under the state (n1,—, nK) are expressed as n • b. The maximum value of the peak bandwidth that the system can achieve is indicated as N . The state boundary that whether a call request of type k VBR service can be accepted again is expressed by n ■ b=N - bk. When the system is in a state that is on the plane region or below the region, it can accept the call request and establish a connection; otherwise, it refuses the call request.

Then, with the complete sharing policy, the CBP of type k VBR service is given by

CBP k =    £   P ( n ) , k = 1, - , K

{ п:п ^ Ь> N - b k }

• 2.3.    The Calculation of Packet Loss Rate and Average Delay

Previously we have assumed that each channel can only transmit a fixed-length packet in a unit of time. Therefore, in a time slot, the probability that j packets have arrived is given by

K

P a ( j ) = ^ \ P (И) п еО I

Zinp\ [ j=n'^b V i=1 У_

Then, the average number of packets having arrived is given by N

N a = Z jP a ( j )                                                                              (5)

j =1

On the assumption that the system's forwarding capacity is C packets per time slot and the service time of every packet is a time slot, in consideration of shared cache mechanism, the packets that the system is incapable of forwarding are stored in the cache within a time slot. The relationship between the maximum length of queue M and the cache size S is represented as M = C + S . The specific queuing discipline is as follows.

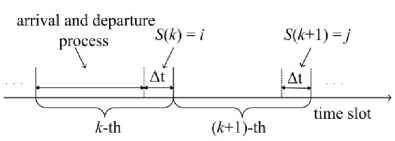
Fig.2. The state of the system in any two adjacent time slots

The packets arriving at any time within a time slot may enter into server device to be forwarded (the length of queue is smaller than C ), or be stored in the caching device (the length of queue is greater than C , but not more than M - 1), or be partially discarded (the length of queue is equal to M ).

The number of packets in the queue constitutes a finite state set in the k -th time slot, which is defined as

S ( k ) e {0,1,2,... . , M }. In order to obtain the formulas for calculating packet loss rate and average delay, we apply queuing theory to analyze the steady-state probability n i of the number of packets. At the same time, we assume that the state of the system is the number of packets in the queue in the time Δt (Δt→0). It is shown in Fig. 2.

So the one-step transition probability from the state i in the k -th time slot to the state j in the ( k + 1 ) -th time slot is given by

Г      P_Q ( j )             0 <  i <  C

P {j/i HP (j + C — i)   C < i < min {j + C, M}

I 0 else

P { M/i }

N

Z Pa ( k )

N

Z Pa ( k )

. k = M + C - i

0 <  j <  M

0 <  i <  C

C <  i <  M

In accordance with (8) and (9) below, we can obtain steady-state probability n i n P = П

M

Z n1

i =0

Provided that the system has i packets in the k -th time slot and the number of the packets that have arrived at the system is j in the (k +1) -th time slot, the number of lost packets in the (k +1 )-th time slot is given by

L m

N

Z( j - M ) Pa ( j )

j = M

N

Z ( j-(M + C - i )) Pa ( j ) j=M + C - i

0 <  i <  C

C <  i <  M

Hence, the average number of lost packets is given by

M

L = Z niLm i=0

And, the packet loss rate is represented as

P l = L / N a

If the number of packets is greater than C in the system at the end of any one time slot, the parts of beyond C packets are delayed at least one time slot. Then, the probability of the packets being delayed i time slot is given by min{( i+1) C, M }

P (i )=   Z П                                                                     (13)

j = iC +1

I M l

[ C J

P d = Z iP ( i )

i =1

• 3.    Numerical Analysis

• 4.    The Joint CAC Algorithm

To verify the correctness of the method that this paper proposes, the following work is to separately discuss the influence of the cache size on the performance of the system. Taking two types of VBR services as an example, parameters are as follows: N = 60, b 1 = 1, b 2 = 3, P _on 1 = 0.3, P _on 2 = 0.4, 5 = 5, a 1 = 40Erl, a 2 = 20Erl, C = 24,25,26.

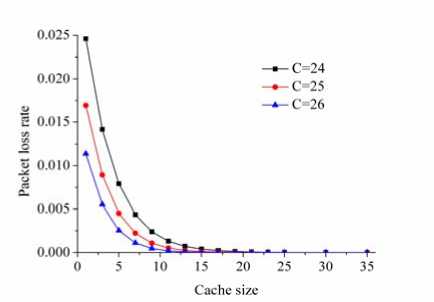
Fig.3. The relationship between the cache size and the packet loss rate

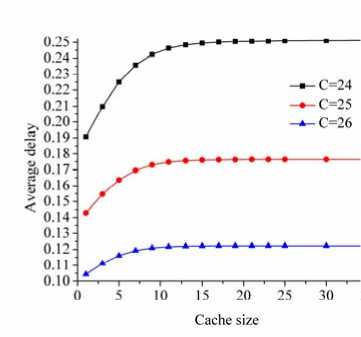
Fig.4. The relationship between the cache size and the average delay

Fig. 3 and Fig. 4 show that, with the increase of the cache size, the packet loss rate is declining while the average delay is increasing in the system. Furthermore, the average delay will not continue to increase after it increases to a certain value, which verifies the effectiveness of the system that allows a relatively small delay but possesses a moderate packet loss rate.

According to numerical analysis, this paper gives the specific CAC policy. The steps of the algorithm are as follows:

• 1,    let N = C , search for the minimum N , which makes the call block probabilities of K kinds of VBR services not exceed their objective values respectively.

• 2,    under this N , search for the minimum S , which does not exceed the objective value of P_L .

• 3,    calculate the minimum P_D , according to the N and the S that are found.

• 5.    Conclusions

Taking two types of real-time VBR services as an example, we give the concrete experimental data of the CAC algorithm. Set the parameters as follows: C = 20, a 1 = 20Erl, a ₂ = 10Erl, b 1 = 1, b ₂ = 3, P on = 0.2, P _o n 2 = 0.25, P" = 1 x 10 ^{- 5}. It can be seen from Table I that different values of N and 5 are obtained with different restrictions and the final objective is the minimization of the average delay P_D . Taking the second group of data as an example, the process of optimization is analyzed as follows: First the minimum of N to meet constraints CBP ₁ ^tar =0.1 and CBP ₂ ^tar =0.3 is N _min =46, such that CBP ₁( N _min)=0.09617, CBP ₂( N _min) =0.279138. Next, with constraints P_L^tar = 1 x 10 ^{- 5}, we find the minimum 5 under N _min, 5 _min =7, such that P_L ( N min , 5 _min) = 9.75 x 10 ^{- 6}. Therefore, the minimum P D is P D ( N _min, 5 _min) =0.00600848. Without adopting CAC algorithm, let 5 =8, N =46, and we obtain P_L = 4.17686 x 10 ^{- 6} and P D =0.00601134>0.00600848. Let 5 =6, N =46, and we obtain P_L = 2.19805 x 10 ^{- 5} >  P_L^,ar and P D =0.00600363. Let 5 =7, N =47, and we obtain P_L = 1.35866 x 10 ^{- 5}> P" and P D =0.0071248>0.00600848. Let 5 =7, N =45, and we obtain P_L = 6.85449 x 10 ^{- 6}, P D =0.00501315 and CBP ₁ = 0.103248> CBP ₁ ^tar . Through comparison, under the same constraints, the algorithm that this paper proposes enables the average delay to achieve optimum.

Table.1. numerical results

Problem		Results
Objective	Constraints	N	S	CBP 1	CBP 2	P L	P D
min( PD )	CBP 1 ar" = 0-5 CBP" = 0.5	35	3	0.190028	0.489048	4.51 x 10 - 6	0.000363682
	CBP 1a" = 0.1 CBP" = 0.3	46	7	0.096170	0.279138	9.75 x 10 - 6	0.006008480

In view of the increasing demand of QoS for real-time service, deploying a moderate shared cache is important. This paper proposes a system model with multi-rate real-time service, which allows a relatively small delay but possesses a moderate packet loss rate. After comprehensive consideration of the performance parameters of the packet-level and the connection-level, this paper proposes the CAC algorithm that optimizes the average delay. The correctness of the algorithm is validated by adjusting the optimized parameters. Further work is planned to take into account other performance parameters, such as jitter and throughput, making the theoretic methods applicable to practical networks.

• [1]    J. Jaramillo and R. Srikant, "Optimal Scheduling for Fair Resource Allocation in Ad Hoc Networks with Elastic and Inelastic Traffic," IEEE INFOCOM 2010 proceedings, San Diego, pp. 1-9, March 2010.

• [2]    S.-Y. Huang and H. Shi, "Performance Study on Multiplex System of Broad Band Real-Time VBR Service and Best Effort Service," Journal of Electronics & Information Technology, Vol. 33, No. 12, pp. 3009-3011, December 2008 (In Chinese).

• [3]    G. Epiphaniou, C. Maple, P. Sant and M. Reeve, "Affects of Queuing Mechanisms on RTP Traffic: Comparative Analysis of Jitter, End-to-End Delay and Packet Loss," International Conference on Availability, Reliability, and Security, Krakow, pp. 33-40, February 2010.

• [4]    J. Y. Kim and G. L. Stuber, "Performance analysis of macrodiversity, voice/data CDMA systems," IEEE Transactions on Wireless Communications, Vol. 5, No. 8, pp. 2111-2118, September 2006.

• [5]    L. Huang and C.-C. J. Kuo, "Joint connection-level and packet-level quality-of- service support for VBR traffic in wireless multimedia networks," IEEE Journal on Selected Areas in Communications, Vol. 23, No. 6, pp. 1167-1177, June 2005.

• [6]    L. Song, L. H. Wu and X. J. Yang, "Call admission control based on degradation and queues in wireless mobile networks," IEEE International Conference on Network Infrastructure and Digital Content, Beijing, pp. 159-163, November 2009.

• [7]    J. Kaufman, "Blocking in a Shared Resource Environment," IEEE Transactions on Communications, Vol. 29, No. 10, pp. 1474-1481, October 1981.

• [8]    G. A. Awater and H. A. van de Vlag, "Exact computation of time and call blocking probabilities in large, multi-traffic, multi-resource loss systems," Performance Evaluation, Vol. 25, No. 1, pp. 41-58, March 1996.