Перистальтическое течение патологической желчи при рубцовом стенозе большого дуоденального сосочка

Перистальтика (от греч. peristaltikós – обхватывающий и сжимающий) – это волнообразное сокращение стенок полых органов (пищевода, желудка, кишечника, мочеточников и т.д.), способствующее продвижению их содержимого. В последнее время перистальтика привлекает большое внимание исследователей из-за важных медицинских применений, таких как движение химуса в кишечнике, перемещение яйцеклетки в маточной трубе, транспорт сперматозоидов, транспорт желчи в желчных протоках, циркуляция крови в мелких кровеносных сосудах. Первые теоретические и экспериментальные исследования по перистальтике были проведены Летхэмом в1966 г. [21].

В дальнейшем появилось множество работ по перистальтике химических растворов, суспензии, а также биожидкостей (кровь, моча, желчь и т.д.).

В работе [30] было изучено течение крови в мелких капиллярах и кровеносных сосудах как течение двухслойной жидкости с центральным слоем, моделируемым жидкостью Кассона [29], и периферийным слоем, как ньютоновской жидкости в трубке с переменным сечением при нулевом числе Рейнольдса и длинноволновой аппроксимации. В дальнейшем исследуемая модель была усложнена при рассмотрении пульсирующего течения крови в сосуде со стенозом [30]. Были получены зависимости безразмерного гидравлического сопротивления от размера стеноза при различных значениях гематокрита для моделей с течением одной и двух жидкостей. Похожая модель, но с учётом периодичного ускорения тела рассмотрена в работе [27].

В [18] было изучено течение мочи в мочеточнике для исследования рефлюкса и эффекта запирания. Было показано, что рефлюкс возникает в верхних мочевых путях при частичном перекрытии волной.

Статья [17] посвящена рассмотрению перистальтики неньютоновской жидкости в расширяющейся трубке (степенная и жидкость Бингама) при различных волновых формах: синусоидальная, треугольная, трапециевидная и квадратная волны. В статье обсуждается влияние типа жидкости (степенная жидкость и жидкость Бингама) на результаты расчетов, а также рассматривается зависимость амплитуды и формы перистальтических волн. Исследованы условия возникновения рефлюкса при различных волновых формах и продемонстрировано, что рефлюкс имеет сильную зависимость от показателя степенной жидкости ( n ), градиента давления и формы перистальтической волны.

Непосредственно исследованию перистальтики течения желчи в общем желчном протоке как несжимаемой ньютоновской биожидкости посвящена работа [25]. Известно, что патологическая желчь – неньютоновская жидкость [ 15], однако авторы статьи рассмотрели течение ньютоновской жидкости в пористом канале, чтобы учесть влияние наличия/отсутствия камней на холединамику. Авторы рассматривают течение жидкости в продольном и поперечном направлениях. Было теоретически найдено условие рефлюкса, которое непосредственно связано с критическим значением градиента давления. Построены зависимости профиля скорости, градиентов давления при различных значениях числа Рейнольдса, пористости, коэффициента Дарси и амплитуды. Часть результатов сравнивалась с результатами работы [16].

Исследования в области биомеханики течения желчи в билиарной системе в последнее время привлекают внимание многих исследователей [8, 9–12, 24]. Патологическое течение желчи вызывает нежелательные напряжения в системе и окружающих тканях, следует отметить, что неблагоприятные поля напряжений могут пагубно отражаться на функционировании организма человека [5].

Большинство работ связано с применением методов вычислительной гидродинамики [13, 19, 20, 26], в частности, с использованием алгоритма взаимодействия жидкость–твердое тело для учёта влияния стенок протоков на характер течения [14, 22, 23].

В статье [19] показано, что патологическая желчь является тиксотропной неньютоновской жидкостью, и найдены параметры модели Каро.

В данной работе рассматривается течение патологической желчи как жидкости Каро в ампуле большого дуоденального сосочка при рубцовом стенозе, моделируемом в виде трубки с сужающимися стенками.

Статья состоит из следующих разделов. В разделе 1 представлены некоторые аспекты анатомии и физиологии течения желчи в билиарной системе и её элементах. Рассмотрена проблема холедохопанкреатического рефлюкса и указана его связь с возникновением патологий поджелудочной железы. В разделе 2 приведены математическая постановка и решение задачи. Найдены аналитические решения для продольной скорости и расхода в зависимости от перепада давления. В разделе 3 представлены результаты решения: зависимости градиента давления от расхода, времени и безразмерной амплитуды для синусоидальной волны, а также даны профили скоростей при различных значениях градиента давлений. Найдены значения градиента давлений, соответствующие условиям возникновения рефлюкса в ампуле большого дуоденального сосочка как трубки с сужающимися стенками.

Анатомия и физиология течения желчи В АМПУЛЕ БОЛЬШОГО ДУОДЕНАЛЬНОГО СОСОЧКА

Желчевыделительная система (билиарная система) предназначена для выведения в двенадцатиперстную кишку секрета печени – желчи, содержащей множество продуктов метаболизма, которые предназначены для выделения во внешнюю среду.

Билиарная система включает в себя желчный пузырь, желчный тракт (пузырный проток, печеночные протоки и общий желчный проток (холедох)), а также систему сфинктеров (рис. 1) [1].

Правый и левый печеночные протоки выходят из печени и соединяются в воротах, образуя общий печеночный проток. Пузырный проток служит продолжением шейки желчного пузыря. Общий желчный проток образуется путем слияния общего печеночного и пузырного протоков [2].

Дистальный сегмент общего желчного протока входит в поджелудочную железу. Общий желчный проток открывается в двенадцатиперстную кишку в области фатерова сосочка, отверстие которого окружено сфинктером [6].

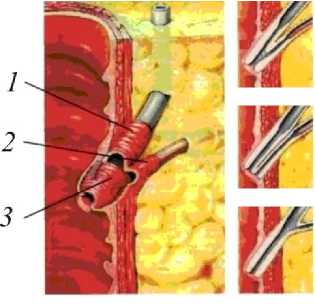
Известно несколько вариантов соединения общего желчного протока с протоком поджелудочной железы в области фатерова сосочка (рис. 2).

Сфинктер регулирует поступление желчи в кишечник и препятствует забрасыванию дуоденального содержимого в желчные протоки. В зоне сфинктера наблюдается два типа моторной активности: базальное давление и фазовая, периодическая сократительная активность. Базальное давление отвечает за регуляцию оттока секрета из желчных и панкреатических протоков [4].

При нарушении сократительной способности сфинктера Одди, например вследствие изменения базального давления, могут возникнуть нарушения регуляции оттока желчи и панкреатического сока из протоков, проявляющиеся в появлении холедохопанкреатических рефлюксов (т.е. патологических забросов желчи в поджелудочную железу, а не в двенадцатиперстную кишку). Именно

Пузырный проток

Шейка

Карман Хартмана

Спиральная заслонка Хайстера

Правый и левый печеночные протоки

Тело

Общий печеночный проток

Дно

Желчный пузырь

Общий желчный проток

Панкреатический проток

Фатеров сосочек

Сфинктер Одди

Двенадцатиперстная кишка

Рис. 1. Билиарная система

Бифуркация перед ампулой а         б

Рис. 2. Анатомические элемен       нктера Одди: а – общая анатомия:

1 – сфинктер общего желчного п         – сфинктер панкреатического протока,

3 – сфинктер ампулы фатерова с       б – варианты строения ампулы сосочка

Бифуркация в ампуле фатерова сосочка

Параллельное расположение протоков холедохопанкреатический рефлюкс тся причиной патогенеза и развития хронического панкреатита (воспалени елудочной железы) [25].

Изучение и моделирование условий возникновения рефлюксов жидкостей в каналах с различной геометрией для помощи врачам при лечении данных патологий является серьёзной задачей биомеханики биожидкостей [3, 7]. В данной статье рассматривается течение желчи как жидкости Каро в ампуле большого дуоденального сосочка (фатерова сосочка), моделируемого в виде трубки с сужающимися стенками, с целью определения количественных критериев, характеризующих такое патологическое состояние, как холедохопанкреатический рефлюкс.

Математическая формулировка проблемы

Рассматривается перистальтическое движение желчи как неньютоновской жидкости в ампуле фатерова соска, представляющей собой трубку длиной L с расходящимися стенками. Длина волны сопоставима с длиной канала ( L ≈λ), поэтому волновое число очень мало, число Рейнольдса также мало. Рассматривается синусоидальная форма волны, бегущей по стенкам. Геометрия стенок может быть описана как

H ' ( x ', t ' ) = b - kx ' + g sin

2n ,  ,      .

— ( x - ct 4

X где b0 – радиус трубы на входе; k – коэффициент наклона стенок; c – скорость волны; x' - продольная координата; g - амплитуда перистальтической волны. Схематично геометрия задачи представлена на рис. 3.

Параметры, использующиеся в модели: b 0 – 3 мм; L – 5 мм; k – 0,5.

Уравнение Навье–Стокса для течения жидкости имеет вид

(dV -   -)

р — + V-W = -V p + V•т, д t где р - плотность жидкости; V - вектор скорости; p - давление; т - тензор касательных напряжений. Учитываем течение в продольном и поперечном направлениях со скоростями и' и v' соответственно.

В проекциях на оси r' и x' в цилиндрической системе координат уравнение (2) может быть записано как ди'     .ди'     ,ди')      др'    1 д , . ч дт , ,

+ v+ и      1 =       +(rт. .) +       , дt      дr'     дx')     дx' r' дrл       J    дx'

[ д v '     ^v '      ,д v '

р    + v + и

Vdt ' д г '       д x '

др '    1 д , , х дт , ,

—— +--(r т..) + ——, dr’ r’dr’v r r ’ дх'

где р',x’ , r '- давление, осевая и радиальная координаты соответственно, а т_г,_х, - напряжение сдвига вдоль направления x’ по нормали к r' ( т_г,_х, =цу ) ;

(.    ди'Л

Y - скорость сдвига I у = — .

V     д r')

В данной работе рассматривается перистальтическое движение неньютоновской жидкости, описываемой уравнением Каро [31]:

m - 1

ц = ц_ю+ ⁽ Ц о ^-П , ^{)(1 + (} a ²-Y ^{2)) 2} ,                             ⁽⁵⁾

где μ – вязкость при нулевом сдвиге; μ_∞ – вязкость при бесконечной скорости сдвига; а и m – константы.

Запишем переменные в безразмерной форме:

r'          и'          Xv' r = —, и = —, v =-- , b o         c        cb 0

x'         ct'           p'             Хт.х, x =    ,   t = Л ,    p =     2 ’    т rx =     2 7  ’ c       X        р c         р c b o ъ H     g                          ' h = —’ Ф = — . b o          b o

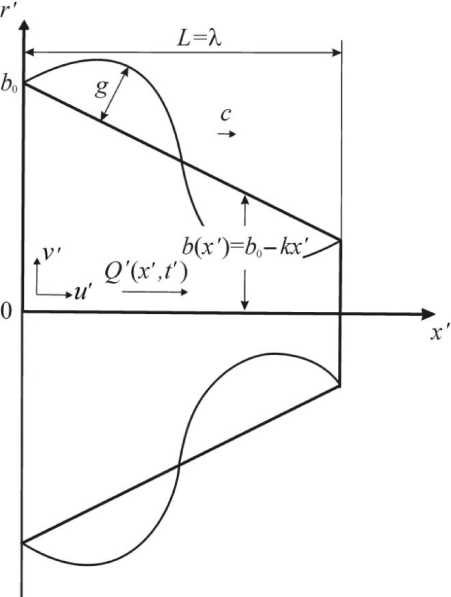
Рис. 3. Схема геометрии течения в осесимметричной трубе с переменным поперечным сечением (проток фатерова сосочка)

Если рассматривать перистальтическое течение в подвижной системе отсчёта и отбросить инерциальные слагаемые, то уравнения (3) и (4) примут вид dp  1 д

& ⁼ r a r ⁽ r ^{T )}, 5 p = о . д r

После упрощений окончательная постановка задачи будет иметь вид ® P = 1 ^д r r„.v + s Y 3 1

д x   r d r^{v L 0       J/}

^ P = 0 при r = 0, д r

X kx и = 0 при r = h = 1--+ ф sin(2n(x -1)), bo

m -1/        x 2

где ^s     ^  ⁽Ц о   И » ) a •

Поскольку 5 мало, найдём решение уравнения и * в виде и* = и ₀ + su_x ,

где u – решение частного уравнения при s = 0; su – «добавка», учитывающая нелинейный характер дифференциального уравнения.

Тогда полное решение имеет вид

( r ² - h ²) д p и * = -------- --+ s

4p₀    д x

( r ⁴ - h ⁴) ^ д p Y 32(p₀)⁴ (a x )

_ ( r ² - h ²) д р

4ц₀    д x

( r² + h ²) ( д р

8( И о )³ (^

•

Расход жидкости через трубу записывается в виде

Q = 2n^S-p r² д x

192( Ц о ) 4

12 r ²ц₀³ - 24 h X³ + | I

Градиент давления Д р вдоль длины L в безразмерной форме может быть найден в виде

L /λ

Выразим dp из (14). Поскольку уравнение (14) является кубическим dx относительно dp , рассмотрим его как dx a1

I - c i Q = 0,

( r ² - 2 h ² )        ( r ⁴ - 3 h ⁴ )

где a = --------- ’-, b = --------/,

¹     16(μ 0 )       ¹    192(μ 0 )⁴

С , =---. Поскольку При r ф 4J3h уравнение (16)

2πr имеет три корня, но только один из них является действительным, тогда решение (16) имеет вид дp dx

^{3 2} 3 ^{a 1}

при r Ф 4/3h , ^,    (17)

cQ при r = л/3 h .

_ a i

Расход в подвижной системе отсчёта

Q ( x , t )   Q       λ kx              ₂₂

-------= —+ 2ф(1--) sin(2n(x -1)) + ф2 sin2 (2n(x -1)). ππ   b где Q(x, t) – средний расход в безразмерном виде.

Результаты и обсуждения

На рис. 4–7 представлены результаты расчётов для патологической желчи как жидкости Каро, параметры которой взяты из работы [19]: а - 0,033; и = 4,5 мПа^с; р₀ = 62,5 мПа^с; m - 0,56. На рис. 4 представлены зависимости безразмерного среднего расхода жидкости от перепада давления при различных значениях φ. Следует отметить, что согласно работе [28], физиологическим течениям соответствует диапазон φ от 0,5 до 0,8. Из рис. 4 видно, что при увеличении амплитуды волны перепад давления существенно возрастает, особенно когда φ превышает значение 0,7. При малых значениях φ разница между перепадом давления незначительная. Также можно отметить, что при Q =0 значение Д Р_Ь максимально и при дальнейшем увеличении расхода градиент давления снижается.

Более того, установлено следующее: при больших величинах объёмный расход жидкости может принимать отрицательные значения, что соответствует возникновению обратного тока жидкости (рефлюкс). Таким образом, величины, при которых Q =0, можно назвать критериями возникновения рефлюкса, т.е. рефлюкс возникает, если ΔP > ΔP .

L L крит

На рис. 5 показаны профили скоростей в канале при различных значениях Δ P . Следует отметить, что профиль течения параболический. Можно заметить, что величина u ^* при увеличении значения Δ P возрастает.

Зависимость Δ P от t для синусоидальной волны при различных значениях Q показана на рис. 6. Из графика видно, что перепад давления достигает своего максимального значения при t = 0,27. В этот момент на входе в трубку возникает схлопывание сосуда, т.е. максимальная окклюзия происходит на входе в трубу, где площадь поперечного сечения является минимальной, следовательно, Δ P получается максимальным. Впоследствии перепад давления убывает до нуля.

На рис. 7 представлена зависимость Δ P от φ для синусоидальной волны. При повышении значения до φ=0,8 Δ P начинает резко возрастать, таким образом, данный результат подтверждает, что при физиологических течениях желчи наблюдается небольшой перепад давления, что соответствует выбранному диапазону φ от 0,5 до 0,8.

Выводы

В статье рассмотрено течение патологической желчи как жидкости Каро в ампуле фатерова сосочка, моделируемого в виде трубки с сужающимися стенками. Получены аналитические решения для продольной скорости и расхода в зависимости от перепада давления. Найдены значения градиента давления, соответствующие условиям возникновения рефлюкса. При увеличении амплитуды волны перепад давления увеличивается, особенно когда φ превышает 0,7. Более того, было показано, что величину перепада давления, при котором Q =0, можно назвать критерием

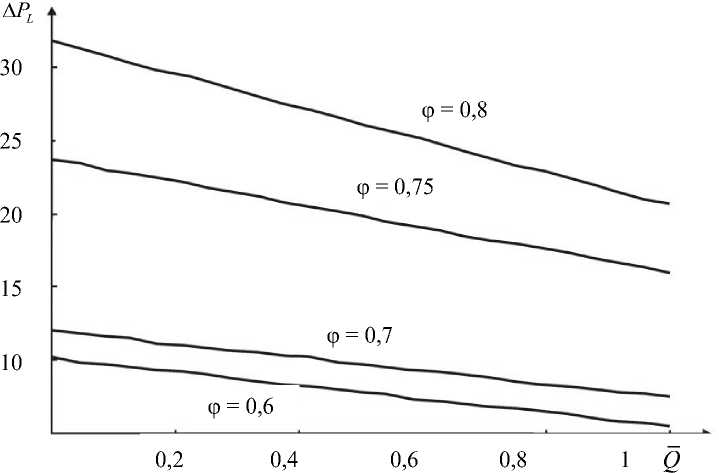
Рис. 4. Зависимость Δ P от Q для синусоидальной волны

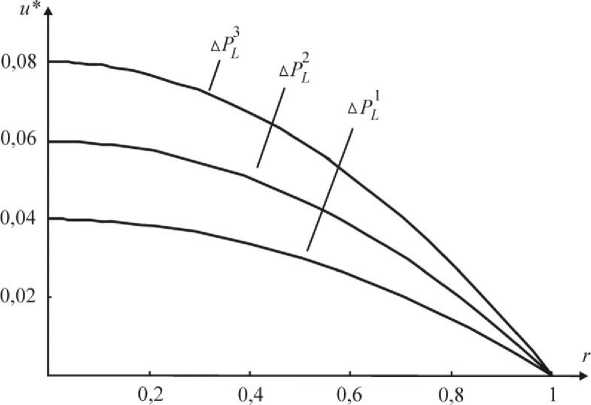
Рис. 5. Профили скорости при ф = 0,5; s = 0,49; ц₀ = 62,5 мПа-с при P¹ = 10, р ² = 15, р ³ = 20

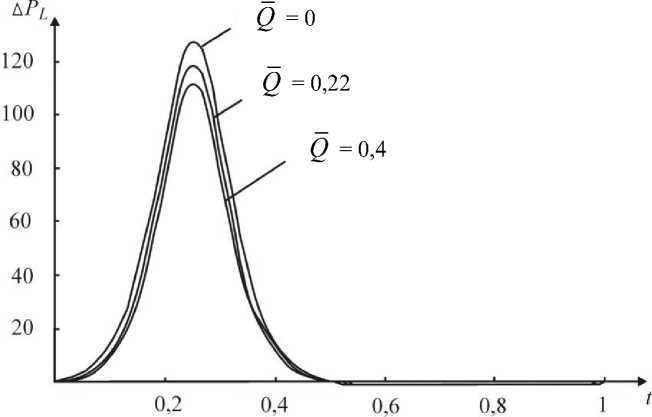
Рис. 6. Зависимость А Р_Л от t для синусоидальной волны (ф=0,6)

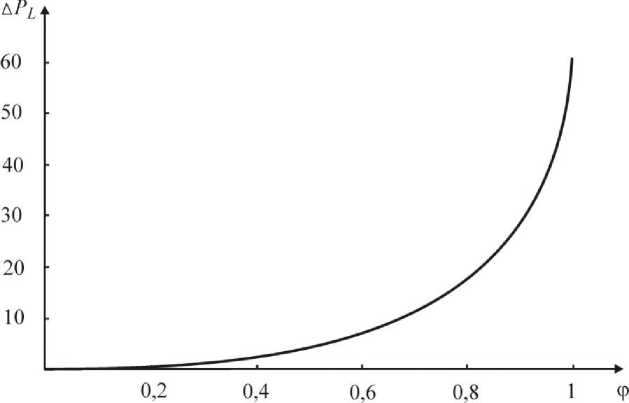
Рис. 7. Зависимость Ар от ф для синусоидальной волны возникновения рефлюкса. Профиль скорости течения в канале имеет параболическую форму, и значение продольной скорости увеличивается с ростом ΔP . Найдены зависимости перепада давления от времени и показано, что при увеличении среднего расхода величина ΔP уменьшается.

Благодарности

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 14-01-31027-мол_а.

450                       ISSN 1812-5123. Российский журнал биомеханики. 2014. Т. 18, № 4: 441–451