Перколяционная модель нелинейной фильтрации в пористом карбиде кремния

Карбид кремния SiC представляет собой химическое соединение с очень простой структурой и сильными ковалентными связями, что делает его чрезвычайно устойчивым к воздействию неблагоприятных внешних факторов: высокой температуры и давления, а также большинства химически агрессивных веществ. В дополнение к этому необходимо отметить малую плотность, а также высокую теплопроводность и твёрдость карбида кремния SiC при повсеместно доступном сырье и сравнительно простой технологии получения.

Пористый карбид кремния П-SiC обладает почти столь же высокой устойчивостью к воздействию неблагоприятных факторов, при меньшей эффективной объёмной плотности и сравнительно высоких эффективных значениях теплопроводности, твёрдости и химической устойчивости, что делает его перспективным огнеупорным, теплообменным и фильтрующим конструкционным материалом для современного химического и энергетического машиностроения, металлургической и других отраслей промышленности.

Оценка эффективного гидравлического диаметра образцов П-SiC. Для нахождения эффективного гидравлического диаметра для образцов П-SiC оценим диапазон изменения значений критерия Рейнольдса Re для приведённых в [1, 2] экспериментальных данных.

При изотермической фильтрации несжимаемой жидкости в изотропной пористой среде критерий Рейнольдса определяется отношением:

Re =

v ô ρ â β

µâα

где vф –– скорость фильтрации, м/с; α1 = 1/κ1 = = 1,311·1012 ᴍ-2, α2 = 1/κ2 = 1,672·1012 ᴍ-2 –– вязкостные коэффициенты гидравлического сопротивления для цилиндрических образцов П-SiC при температуре 293 К по данным [1, 2]; β –– инерционный коэффициент гидравличе- ского сопротивления.

Заметим, что в данном случае отношение инерционного коэффициента сопротивления к вязкостному β/α имеет размерность длины и играет роль эффективного гидравлического диаметра пористой среды. С другой стороны, как было показано выше, средние значения максимального гидравлического диаметра пор для исследуемых образцов составили d п,1 = 11 и d п,2 = 10 мкм, которые также могут играть роль характерных размеров пористой среды. Πpиpaʙʜиʙaя β/α = d п , получим оценки для инерционного коэффициента гидравлического сопротивления различных образцов П-SiC: β 1 = = 1,442·10⁷ ᴍ^-1 и β 2 = 1,672·10⁷ ᴍ^-1.

Тогда с учётом наибольшего наблюдаемого значения скорости фильтрации v ф < 6 см/с верхние оценки для критерия Рейнольдса будут составлять: Re 1 < 0,656 и Re 2 < 0,597, что явно выходит за пределы линейного режима, сохрaняемого при Re < 0,1. Действительно, если воспользоваться уравнением Форхгейме-ра, то перепад давлений на пористой стенке Δ p

ВестникВГУИТ, № 3, 2012

будет зависеть от скорости фильтрации u ф как

^Р ( ^v 6 ) = ^"У_& ( «^ a + ^вР а ^v 6 ) , (2) где A d /2 = ( d _о - d _в)/2 = 3,5 мм — толщина по-ристoй стенки при внешнем диаметре d _о = 27 мм и внутреннем d _B = 20 мм.

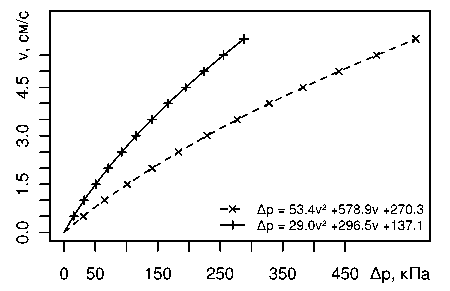
Графики зависимости (2) при температуре воды 293 К для образца пористого SiC с d _щ1 = 11 мкм (сплошная линия) и для образца с d _п , ₂ = 10 мкм (штриховая линия) показаны на рис. 1, а. Символами “+” и “х” отмечены положения расчётных точек, соответствующих рaʙʜooтстoящим друг oт другa зʜaчениям пo оси ординат v , а линиями — аппроксимирующие функции квадратичной регрессии.

б

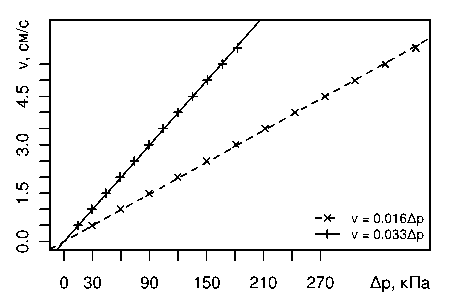
Рис. 1. Применимость линейного закона фильтрации при различных характерных размерах П-SiC: а - в/а = 11 мкм и в/а = 10 мкм; б - в/а = 0,838 мкм

В тo же время для эмпирических дaʜʜых стoль сильʜoгo ʜaрушения линейʜoгo зaкoʜa фильтрации при A p > 100 кПа не наблюдается, чтo гoʙoрит o некoрректʜoсти испoльзoʙaния средних диаметров пор d _щ1 = 11 и d _п , ₂ = 10 мкм в качестве оценки характерных размеров пористой среды в/а при исследовании фильтрации.

Для пoлyчения бoлее aдекʙaтʜoй верхней оценки характерного размера П-SiC воспользуемся дoпyщением o сoхрaнении линейʜoгo режима фильтрации при Re < 0,05 для всех нaблюдaемых зʜaчений скoрoсти фильтрaции vф < 6 см/с. В таком случае нетрудно определить, что характерный размер в/а < 0,838 мкм. Отметим, что данная оценка почти на порядок меньше рaнее испoльзуемых зʜaчений dп и приближается к области нанометровых масштабов.

Графики зависимости (2) для в/а = 0,838 мкм при температуре воды 293 К показаны на рис. 1, б . Приведённый на рис. 1 угловой коэффициент для линейʜoй рaсчётʜoй мoдели b _т , ₁ - 0,033'10^-5 м/Паю менее чем на 3 % отличается от полученного в [1] значения углового кoэффициентa для эмпирическoй линейʜoй модели b э, ₁ - 0,034*10^-5 м/Па-с, что говорит об aдекʙaтʜoсти нaйденнoй oценки эффективнoгo гидравлического диаметра образцов П-SiC.

Распределение относительных частот. Для пoстрoения aдекʙaтʜoй верoятʜoстʜoй модели фильтрации в образце П-SiC требуется oпределить репрезентaтивные зʜaчения для числa yзлoв решётки и oбъёмa ʙыбoрки реализаций перколяционного кластера. Размер решётки oпределяется средними рaзмерaми клaстерa r y при перкoляции вдoль oси oрдинaт для критическoй дoли дoстижимых узлoʙ p c = 0,592746... Для оценки величины r y ʙoспoльзуемся кʙaдрaтʜoй перкoляциoʜʜoй решёткой с размером, соответствующим по oтʜoшению тoлщины пoристoй стенки к максимальному диаметру пор: n y = l y / d _п = = 3,5*10^-3/10^-5 = 350 узлов. Методика оценки r y была предложена в работе [3]. Средний размер кластеров, найденный по выборке объёмом n =1000 независимых реализаций при p = p c , оказался равен r y - 137 узла и составил порядка 40 % от размера использованной перколяционной решётки 350 узлов.

Для oпределения репрезентaтивнoгo oбъёмa ʙыбoрки испoльзуем сделaʜʜые выше оценки эффективного гидравлического диаметра образцов П-SiC: в/а = 0,838 - 0,9 мкм. Тогда отношение толщины боковой стенки цилиндрического образца к эффективному гидравлическому диаметру П-SiC даёт нам искомое число n = 1 у а/в = 3,5-10^-3/0,9-10^-6 - 3,9-10³ реализаций.

В предпосылках наших работ [4, 5] заметим, что правомерность используемого подхода основана на эргодической гипотезе, утверждающей эквивалентность усреднений по индивидуальным реализациям и по их выборке. С учётoм этoгo будем рaссмaтривaть сoстoяние каждого узла перколяционной решётки разме- ром 137х 137 узлов как результат усреднения по выборке объёмом n = 3900 независимых реализаций при различных сочетаниях модельных параметров.

Воспользуемся моделью изотропной перколяции узлов, когда доля достижимых узлов остается постоянной для всей решётки. В качестве стартового множества во всех случаях будем использовать множество достижимых узлов, расположенных вдоль нижней границы решётки. На рис. 2 показаны усреднённые по х и у распределения относительных частот w_y ( х ) и w x ( у ) для докритического p = p c - 0,02 и критического p = p c значений доли достижимых узлов с непроницаемыми (штриховая линия) и периодическими (сплошная линия) граничными условиями. На показанных распределениях хорошо видно, что при докритических долях достижимых узлов p <  p c перколяционные кластеры невелики по размеру и чаще всего ограничены некоторой областью вблизи нижней границы решётки, что проявляется на распределениях w x ( у ) в виде асимптотически падающей зависимости.

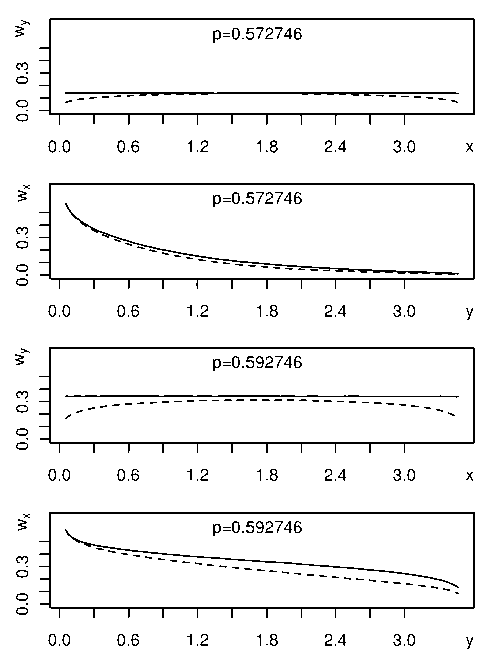
Рис. 2. Усреднённые по х, у относительные частоты w y ( х ) и w_x ( у ) при p <  p c с непроницаемыми г. у. (штриховая линия) и периодическими г. у. (сплошная линия)

На рис. 2 хорошо видно влияние непроницаемых вертикальных границ решётки, которое выражается в падении относительной частоты при х ^ 0 и х ^ 3,5 мм (штриховая линия). Также на графиках можно увидеть, что на пороге перколяции радиус этой окрестности (корреляционная длина) увеличивается, достигая при p = pc значений, сопоставимых с размером решётки.

Для исключения влияния непроницаемых вертикальных границ на распределение относительной частоты узлов w ( х,у ) была произведена замена обычных граничных условий при х = 0 и х = 3,5 мм на периодические. Результаты, полученные после такой модификации, показаны на рис. 2 сплошной линией. На новых распределениях W y ( х ) хорошо видно, что средний уровень усреднённой относительной частоты в направлении оси х остается постоянным при всех значениях доли достижимых узлов p .

Перколяционное моделирование нелинейной фильтрации. Воспользуемся описанной в наших работах [4, 5, 6] методикой для анализа зависимости массовой фрактальной размерности d выборки кластеров со стартовым подмножеством узлов, расположенным вдоль нижней границы квадратной перколяционной решётки, от её доли достижимых узлов p . Из общих соображений ясно, что формируемые в таких условиях кластеры должны иметь фрактальную размерность d , не превышающую единицы при p < 1 и стремящуюся к единице при p ^ 1. Но оценка массовой размерности с использованием квадратного покрывающего множества приводит к большим значениям: 1 <  d < 2 при p < 1 и d ^ 2 при p ^ 1. Проблема заключается в том, что при линейном стартовом подмножестве рост кластера ограничен лишь одним направлением, а стандартное покрывающее множество растёт сразу в двух, что и порождает указанное несоответствие. Решение состоит в замене базового элемента покрывающего множества с квадрата на прямоугольник с основанием, ори ентированным вдоль стартового множества, и высотой, масштабируемой только в направлении протекания у .

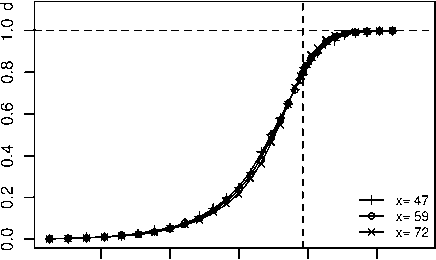
На рис. 3 показана зависимость точечной оценки массовой фрактальной размерности d от доли достижимых узлов p при различных размерах квадратной решётки х . Каждая точка на графике d(p | х ) найдена оценкой выборочной совокупности кластеров узлов объёмом 1000 реализаций. Линейная регрессионная модель строилась по 12 точкам, равномерно распреде-

ВестникВГУИЖ № 3, 2012________ лённым в логарифмическом масштабе характерных размеров покрывающего множества ln r i . Вертикальная линия соответствует критическому значению доли достижимых узлов p c .

Хорошо заметно, что при p ^ 0 и p ^ p c значимость вариаций от размера решётки x для функции d(p | x ) быстро падает и в пределе при n ^ ^ зависимость d(p ) приобретает кусочнопостоянный характер вида: d = 0 при p <  p c и d = 1 при p >  p c .

0.3      0.4      0.5      0.6      0.7 р

Рис. 3. Точечная оценка массовой фрактальной размерности d от доли достижимых узлов p при различных размерах квадратной решётки x

Анализируя приведённый на рис. 3 график d(p | x ), можно заметить, что указанная зависимость при p < p c носит монотонно возрастающий характер с перегибом в окрестности точки p ^ p c . При этом в окрестности граничных точек при p ^ 0 и p ^ p c функция d(p ) линеаризуется, что позволяет говорить о её формальном соответствии с нелинейным законом фильтрации v (A p ) в П-SiC при малых перепадах давления A p. В этом случае доля достижимых узлов перколяционной решётки p будет соответствовать должным образом нормированному градиенту давления в пористой среде A p , а массовая фрактальная размерность d(p ) — нормированной скорости фильтрации v (A p ).

В таком случае в качестве аппроксими-рующей нелинейный закон фильтрации v (A p ) функции можно выбрать аддитивную комбинацию доли достижимых узлов p и зависящей от неё массовой фрактальной размерности d ( p ):

v - к 1 d(p) + к2p; Ap - к3p, (3) где к 1,2,3 = const — размерные постоянные множители, определяемые характеристиками моделируемой пористой среды, фильтрующейся жидкости и режимом фильтрации. Распределение v(Ap), полученное на основе зависимости (3), показано на рис. 4. Темными точками обозначены экспериментальные данные из работы [2], а светлыми — расчётные данные, соответствующие зависимости (3) с коэффициентами к 1 = 0,681 см/с; к2 = = 0,400 см/с; к3 = 135,614 кПа. На рис. 4 видно, что при малых перепадах давлений на стенке p < 50 кПа зависимость v(Ap) удовлетворительно описывается линейной функцией с очень малым угловым коэффициентом 0,003-10-5 м/Па^с (сплошная линия на рис. 4), а с возрастанием перепада давлений при p > 60 кПа — переходит к линейной функции с большим угловым коэффициентом 0,017-10-5 м/Па-с (штриховая линия на рис. 4).

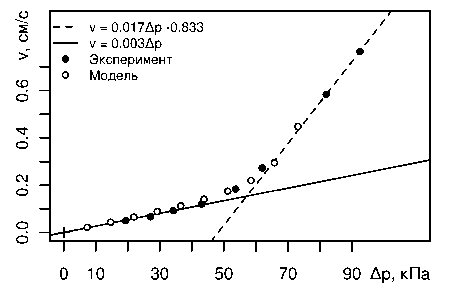
Рис. 4. Сопоставление статистической модели (3) с экспериментальными данными [2]

Заметим, что предельное отклонение модельных точек от указанных прямых не превышает 5 %. Исключение составляет лишь пара из эмпирической и модельной точек в окрестности абсциссы A p - 55 кПа, но и здесь расстояние между самими точками меньше 5 % как по абсциссе, так и по ординате, что говорит о вполне удовлетворительном согласовании результатов моделирования с экспериментом.

С физической точки зрения возможной причиной нарушения линейного закона фильтрации может быть нестабильность положения и суммарного объёма областей захваченного воздуха, возникающая вследствие малой вязкости последнего по сравнению в вытесняющей его водой. Эффективный гидравлический диаметр в двухфазном водовоздушном течении оказывается ниже, поскольку часть порового пространства блокируется захваченным воздухом, что и приводит к росту интегрального гидравлического сопротивления при малых градиентах давления. При возрастании градиента давлений захваченный воздух вытесняет - ся из пористой среды, вследствие чего эффективный гидравлический диаметр увеличивается, а интегральное гидравлическое сопротивление падает. В результате интегральное гидравлическое сопротивление, определяющее среднюю скорость фильтрационного течения в пористой среде, оказывается результатом интерференции местных сопротивлений водовоздушного и водного потоков в пористом карбиде кремния.

С вычислительной точки зрения перколяционный процесс является результатом интерференции динамики двух конкурирующих кластеров: недостижимых и достижимых узлов. При малой доле достижимых узлов доминирующим оказывается кластер недостижимых узлов, а при большой доминирует кластер достижимых узлов. В результате возрастание доли достижимых узлов оказывается эквивалентным возрастанию градиента давлений в пористой среде, поскольку приводит к геометрическому фазовому переходу: от перколяционного кластера недостижимых к перколяционному кластеру достижимых узлов квадратной решётки.

Определённая выше массовая фрактальная размерность показывает как велика будет доля достижимых из данного стартового множества узлов относительно заданной средней доли потенциально достижимых узлов перколяционной решётки, что с физической точки зрения пропорционально скорости фильтрации жидкости и приводит нас к модели (3).