Персонализация параметров аорты для постановки граничных условий в одномерной модели коронарного кровотока

RUSSIAN JOURNAL OF BIOMECHANICS

Ишемическая болезнь сердца (ИБС) продолжает оставаться одним из самых распространённых сердечнососудистых заболеваний в развитых странах. Основной причиной ИБС является стеноз (сужение просвета) коронарных артерий, как правило из-за атеросклеротических бляшек. Для определения функциональной значимости стеноза широко применяется фракционный резерв кровотока (ФРК) [1-3]. ФРК вычисляется как отношение среднего давления после стеноза к среднему давлению в аорте при гиперемии. Для определения среднего давления за стенозом требуется операция и использование одноразового внутрисосудистого датчика давления. Для оценки ФРК без использования операции и дорогостоящих датчиков широко применяются методы моделирования кровотока [4–7]. Точность таких моделей в полной мере зависит от корректной постановки граничных условий, особенно параметров аорты, которые определяют взаимодействие коронарной сети с системным кровообращением.

Традиционные одномерные модели кровотока [7-11] несмотря на вычислительную эффективность, обладают рядом ограничений, связанных с упрощением физиологии кровообращения. Их ключевой недостаток - неспособность адекватно воспроизвести пространственно-временную динамику волн давления в аорте, критически важную для корректного описания диастолического давления и взаимодействия коронарных артерий с системным кровотоком. Упрощенное представление сосудов в виде одномерных трубок игнорирует локальные изменения эластичности стенок, неравномерность геометрии аорты и влияние отраженных волн, что приводит к артефактам в профиле давления и заниженной точности прогнозирования гемодинамических параметров [9]. Кроме того, ручная калибровка таких моделей для конкретных пациентов, включающая подбор жесткости сосудов и граничных условий, остается субъективной и ресурсоемкой, что ограничивает их применение в клинической практике, где требуется высокая степень персонализации. Эти ограничения актуализируют необходимость разработки адаптивных алгоритмов, способных динамически корректировать параметры модели на основе данных in vivo , сохраняя баланс между сложностью и достоверностью.

Целью данной работы является разработка алгоритма автоматической персонализации параметров аорты в одномерных моделях коронарного кровотока. Новизна исследования заключается в постановке граничных условий на аорте в виде модели эластичного резервуара и реализации алгоритма для их численной реализации. Параметры граничного условия подбираются с помощью алгоритма динамической адаптации в течение нескольких сердечных циклов, что позволяет достигать целевых значений систолического и диастолического давления без ручных корректировок. Модель кровотока сочетает одномерную гидродинамическую модель с модифицированной моделью эластичного резервуара (Windkessel-модель). Численная реализация включает метод Ньютона для решения нелинейных уравнений и оптимизацию параметров через итерационную корректировку на каждом третьем сердечном цикле.

Предложенный метод валидирован на обезличенных клинических данных. Результаты демонстрируют, что автоматическая оптимизация позволяет значительно улучшить соответствие модели реальным физиологическим профилям давления. Это открывает перспективы для интеграции алгоритма в системы поддержки врачебных решений, например, для неинвазивной оценки ФРК.

Материалы и методы

Одномерная модель кровотока

Кровоток в коронарных сосудах представляется течением вязкой несжимаемой жидкости по сети одномерных эластичных трубок. Течение подчиняется законам сохранения массы и импульса [1]:

dA , d(Au-) = с 51      5x duL+_df uL+Pk

dt   dx I 2 p

u

- 22 np- k

где k - индекс сосуда, t - время, x - расстояние вдоль сосуда от точки соединения сосудов, p = 1,06 г/см³ - плотность крови, р = 4 сПуаз - вязкость крови [12], A_k ( x,t ) - площадь поперечного сечения сосуда, p k - давление крови, u_k ( x, t ) - линейная скорость, усредненная по поперечному сечению. Связь между давлением и площадью поперечного сечения сосуда задается соотношением

Pk ( A k ) ^- P *k = P c k f ( A k ) ,                (2)

где f(A) - монотонная S-образная функция, которая задается как f (Ak )=

<

exp ( Aki A^{0 -} 1 ) ^- 1, Ak >  A k

In ( AklA O ) , A k ^ A 0

p *k  - давление в тканях, окружающих сосуд,

C k - скорость распространения малых возмущений, 0

A - площадь поперечного сечения сосуда в покое.

Граничные условия

На входе в сосудистую сеть задается граничное условие в виде потока крови:

SV 'П ■ ( Т„, _r- T }

Q =  -------Г sin I П —---- I , in 2 (T - T)   ^  Tf - Ts J                14

Pk + 2₽ uk

= const ,

где SV - ударный объем, T cur - текущее время с конца последнего сердечного цикла в модели, T f - конец активной фазы притока крови, T s - старт активной фазы притока крови.

На выходе из терминальных сосудов задается сопротивление и давление на выходе:

P, - P out = R k • Qk ,                    (5)

где R k рассчитываются итерационным методом в соответствии с законом Мюррея [7], P_out - давление в венах после микроциркуляции, которое подбирается персонально для каждого пациента, Q k (x, t) - поток крови k -том сосуде.

Интегральное сопротивление рассчитывается через сердечный выброс и среднее давление пациента:

R =

mean     out

CO

где CO = HR • SV /60, HR - частота сердечных сокращений.

В местах соединения нескольких сосудов граничные условия формулируются на основе фундаментальных физических принципов. Согласно закону сохранения массы, суммарный поток крови, поступающий в узел разветвления, равен суммарному потоку, покидающему его, что математически выражается уравнением:

Z Q .n = Z Q out                  (7)

где Q in и Q_out - объемные расходы во входящих и исходящих сосудах. Дополнительно применяется условие Бернулли, обеспечивающее непрерывность полного давления в узле:

где k принимает значения индексов всех сосудов в точке ветвления [12].

Это позволяет согласовать гидродинамические параметры в зоне соединения и избежать физиологически нереалистичных скачков давления [12]. Такие условия важны для моделирования волновых процессов, включая отражения и рефракцию, в реалистичных сосудистых сетях.

Аорта: одномерная модель и модель Windkessel

Первый вариант модели кровотока включает в себя «виртуальную» аорту - искусственный сосуд, который обеспечивал растяжимость и сопротивление большого круга кровообращения. Параметры виртуальной аорты подбирались так, чтобы получить профиль давления, максимально близкий к физиологичному. Структура расчетной области для данной модели представление на Рис. 1. Корень аорты и виртуальная аорта являются отдельными одномерными сосудами. В месте стыковки корня аорты, виртуальной аорты, правой коронарной артерии (ПКА) и левой коронарной артерии (ЛКА) задаются условия вида 7–8. Структура ЛКА и ПКА извлекаются из снимков компьютерной томографии пациента [15].

Во втором варианте модели виртуальную аорту и ее корень предлагается заменить моделью упругого резервуара ( Windkessel) [9].

Модель Windkessel - математическая модель, описывающая динамику кровообращения, в первую очередь в крупных артериях (рис. 2). Она представляет артериальную систему как комбинацию сопротивления ( R ), емкости ( С ), а в расширенных версиях - и инерции ( L ). Эти компоненты отражают основные свойства

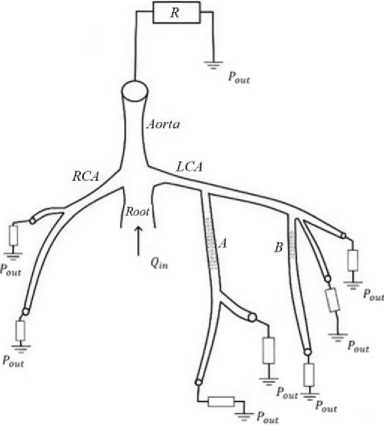
Рис. 1. Одномерная модель с виртуальной аортой

^out

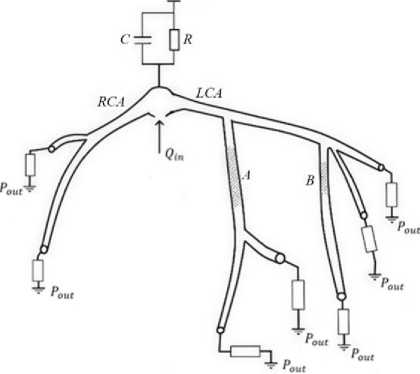
Рис. 2. Одномерная модель с Windkessel моделью

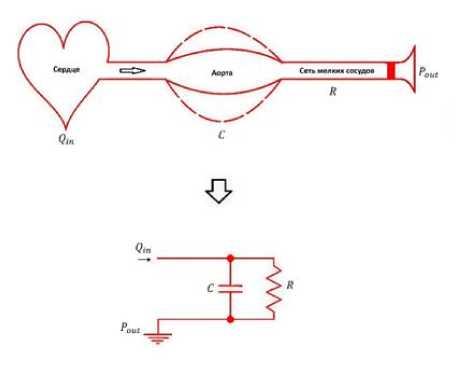
Рис. 3. Физический смысл модели Windkessel и ее аналогия с электрической цепью

сосудов: сопротивление потоку крови, их эластичность и инерционные эффекты. Модель используется для анализа артериального давления, пульсовых волн и взаимодействия системного кровообращения с работой сердца. Ее простота обеспечивает вычислительную эффективность, а точность достаточна для большинства задач гемодинамики. Однако она ограничена в описании сложных волновых процессов и локальных эффектов. На рис. 3 показано представление модели Windkessel и электрической цепи, которая ей соответствует. Модель описывает динамику давления в эластичном резервуаре (аорте), на входе в который подаётся поток Q(t) . На выходе резервуара установлено постоянное давление P out (давление в венах).

Уравнение двухэлементной модели Windkessel [13; 14]:

Р-Р рр

Q (t ) = P '+CdP, (9) R dt где PA – давление в аорте, R – периферическое сопротивление, C – растяжимость аорты.

Структура расчетной области (рис. 2) включает правую и левую коронарные артерии, геометрические параметры которых (топология, диаметр, длина) реконструируются на основе данных компьютерной томографии.

Устья артерий соединены с аортой, граничные условия для которой задаются через входной объемный поток Q in и двухэлементную модель Windkessel , имитирующую гемодинамику большого круга кровообращения.

В отличие от первого варианта модели (рис. 1), где используется виртуальная одномерная аорта, в данной работе она полностью исключена.

Вместо этого применена модель Windkessel с параметрами R и C , автоматически калибруемыми для минимизации отклонений от целевых значений систолического и диастолического давления.

Уравнения для расчета в точке соединения левой и правой коронарных артерий:

' Q in = ^Q a + ^U L ^A L ^{+ U} R ^A R ,

P -P    dP

Q a = P-T o^ + C-P A ’ R       dt

• < u_L = ^a _lA_l + p _l ,

• ^U R = ^a R ^A R ⁺ P R ,

P = P = P

P A P R P L ,

где P_R = P ( A_r ) , p = P ( A_l ) - давления в правой и левой коронарных артериях, A L , A R – площади поперечного сечения левой и правой коронарных артерий.

Первое уравнение представляет собой закон сохранения массы. Поток из сердца Q in делится на три потока: поток в аорту, поток в левую коронарную артерию и поток в правую коронарную артерию. Поток в аорту расписан через модель Windkessel . Второе и третье уравнения являются дискретизацией гиперболических уравнений вдоль характеристик, покидающих область расчета [12]. Эти уравнения называют условиями совместности. Последнее уравнение предполагает непрерывность давления в области отхождения правой и левой коронарных артерий.

Для дискретизации производной давления по времени была применена следующая схема:

dP^ P, — P - , dt      A t_n

Pt-1 – давление на предыдущем шаге по времени в правой коронарной артерии, которое равно давлению в аорте, Atn - шаг по времени.

Расчет ведется по двум неизвестным площадям – A L , A R .

Для решения системы нелинейных уравнений был использован метод Ньютона:

X n + , = x_n -[ J x ]^{- 1} Д, n = 0,1,2,3...,        (11)

где f = f (x) = 0 - система уравнений, J xi d Xj

якобиан системы.

Преобразовав систему (10), можем прийти к системе из двух уравнений:

Далее необходимо вычислить элементы якобиана:

Для модели, емкость расчета

dt = 2a A, +P,, aal      l l L af1   aPR (1 c >       , n

---=        +    + 2a о Ar + в„, aA  aA к R at)    R R ^R d f 2 _ aPl

a a_l   a a_l ’

5 f    a p„

2R dA„    dA„

RR

первоначальной оценки

cur      prev

P out _cur

таких параметров

как давление на выходе P out и артериальная C были использованы следующие формулы для стартовых значений и последующей

PPc

PPt

= P„„ out prev

±| P min - P d\

где PPc – разность наибольшего и наименьшего давлений после каждого третьего сердечного цикла, PPt – разность заданных давлений пациента, P min – минимальное давление цикла, P d – заданное диастолическое давление, C prev и P out – параметры до корректировки, C cur и P out – параметры после корректировки.

Результаты

оптимизации:

P ou, = 0,7 DBP ,

SV

PP

где DBP – заданное диастолическое давление, а PP – разность систолического и диастолического давлений [16].

Первоначальные оценки параметров корректируются в ходе выполнения расчётов для того, чтобы достичь целевых значений систолического и диастолического давлений. Корректировка проводилась каждый третий сердечный цикл. На протяжении цикла вычислялись максимальное и минимальное давление в аорте, которые принимались соответственно за систолическое и диастолическое. Затем, если разность получившихся давлений не соответствовала заданной, то артериальное сопротивление C изменялось пропорционально частному заданной и вычисленной разностям давлений. Аналогично при несоответствии вычисленного диастолического давления заданному изменялось и значение давления на выходе P out :

Модель с виртуальной аортой хорошо воспроизводит среднее давление пациента, однако профиль давления в диастолу воспроизводится неточно. Неправильно подобранные параметры вызывают нефизиологичные отражения волн от конца виртуальной аорты, что влияет на профиль давления (Рис. 3). В результате этого и сложности подбора параметров аорты для конкретного пациента было принято решение модифицировать модель кровотока и заменить виртуальную аорту моделью Windkessel (эластичного резервуара).

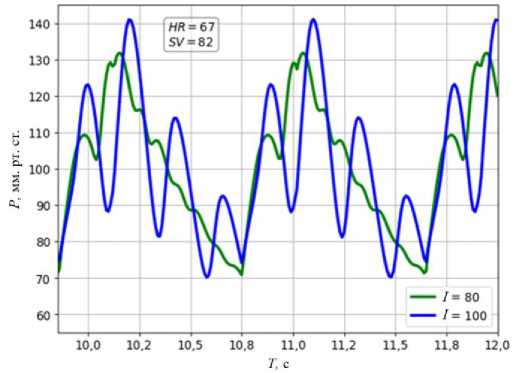
Для решения проблемы нефизиологичности профиля давления в аорте, который получается с помощью модели с виртуальной аортой, был введен механизм автоматического подбора параметров растяжимости сосуда и давления на выходе.

В течение каждого третьего сердечного цикла модель запоминает наибольшее и наименьшее давление в точке сочленения правой и левой коронарных артерий, которые принимаются за систолическое и диастолическое давления соответственно. Затем перед началом нового сердечного цикла изменяются параметры в соответствии с заданными значениями давлений вида 15.

Рис. 4. Давление в аорте за последние 2 сердечных цикла при значениях длины виртуальной аорты 80 см и 100 см

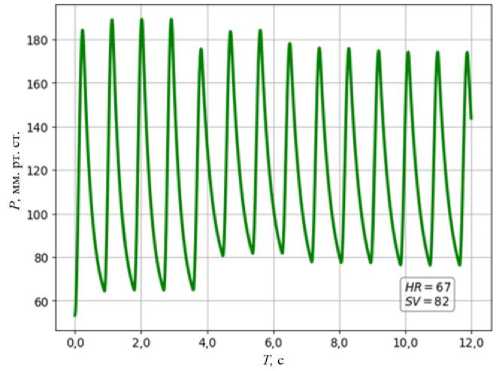
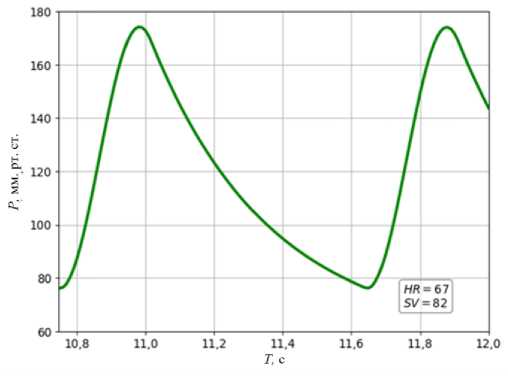
Рис. 5. Корректировка профиля давления в аорте к целевым значениям пациента P d =76, P s =174

Рис. 6. Давление в аорте на последнем расчетном цикле, полученный с помощью модифицированной модели

Рис. 5 демонстрирует процесс адаптации модели для достижения целевых значений систолического и диастолического давлений для конкретного пациента.

Цикл давления после подбора параметров можно увидеть на Рис. 6. Профиль давления более физиологичен, чем на Рис. 4 – отсутствуют лишние пики и отражения, при этом отпадает необходимость в сложной настройке параметров аорты.

Расчеты выполнены на обезличенных клинических данных пациента с использованием двух модификаций модели. Вторая версия, основанная на гибридном подходе (одномерные уравнения + адаптивная модель Windkessel),    продемонстрировала    значительное улучшение: значение фракционного резерва кровотока для рассматриваемого стеноза ФРК = 0,91 приближено к инвазивно измеренному    ФРКинв = 0,89    более, чем значение, полученное моделью с виртуальной аортой ФРК = 0,85. Физиологичность профиля давления улучшилась за счет устранения артефактов отражения волн, характерных для одномерного представления аорты. Это подтверждает, что гибридная модель не только эффективнее в вычислительном аспекте, но и обеспечивает более точную и стабильную персонализацию граничных условий, что критично для клинического применения. Новая модель позволила лучше оценить инвазивно измеренное значение ФРК, при более физиологичном профиле давления в аорте, а также позволило на 40 % уменьшить время работы модели в результате того, что отпала необходимость в просчете значительного количества расчетных точек, расположенных    вдоль    виртуальной    аорты