Перспективы создания оптических аналоговых вычислительных машин

Цифровые вычислительные машины имеют ряд принципиальных недостатков, которые необходимо учитывать при создании автоматизированных систем управления движением объектов, таких как космические и летательные аппараты, морские суда и т.д.

В первую очередь, это сама дискретная форма представления данных, которая неизбежно приводит к «округлению» и неточности представления информации. Увеличение разрядной сетки процессоров позволяет уменьшить неточности, но принципиально не решает проблему: ошибки остаются и, более того, накапливаются при выполнении большого количества операций, что приводит к проблеме численной устойчивости вычислительных алгоритмов [1].

Кроме того, решение целого класса задач, основанных на решении дифференциально-интегральных уравнений и лежащих в основе многих задач управления движением, в силу конечно-разностной природы алгоритмов вычисления требует значительных расчётных затрат (в сравнении с простыми операциями) [2]. Это делает затруднительным (дорогостоящим или даже невозможным) применение таких решений в автономных системах оперативного управления, требующих решения задач в режиме реального времени.

Также следует отметить, что полупроводниковая элементная база компьютеров достаточно чувствительна к условиям окружающей среды: к температуре, электромагнитным возмущениям, радиации.

В то же время аналоговые вычислительные машины (АВМ) [3 -4] лишены многих из указанных недостатков. АВМ, существовавшие до экспансии цифровой техники, успешно справлялись со своими задачами и используются до сих пор в системах оборонного назначения. Самыми распространёнными и технически совершенными являлись АВМ на основе электрических элементов.

Сравнение АВМ и цифровых вычислителей показывает, что, хотя АВМ тоже выполняют расчёты с погрешностью (правда, она имеет иную причину), они более выигрышны при решении сложных задач, поскольку по своей природе позволяют получать решение в реальном времени. Однако АВМ менее универсальны: в них элементы и структура их взаимодействия определяют и обрабатываемые данные, и способ их обработки, в то время как в цифровых вычислительных машинах элементная база, данные и программа являются различными сущностями, причём изменяемыми почти независимо друг от друга. Именно универсальность, выражающаяся в возможности использования одного и того же компьютера для решения бесконечно широкого спектра задач, и привела к вытеснению АВМ по мере увеличения быстродействия компьютеров.

В последние годы стала актуальной задача создания АВМ на оптической элементной базе. Предпосылками к этому послужили работы в области разработки и исследования различных устройств фотоники (в т.ч. фотонных кристаллов [5, 6] и брэгговских структур), сформированные научная база и технологии изготовления дифракционных оптических элементов (ДОЭ) [7, 8]. Причём современные технологические процессы позволяют изготавливать оптические элементы с высокой точностью, вплоть до нескольких нанометров. Кроме того, стали доступными источники когерентного излучения с различными характеристиками (в т.ч. лазеры с настраиваемой длиной волны), разработаны технологии производства разнообразных оптических волноводов, широкое распространение получили волоконно-оптические линии связи.

Следует уточнить, что речь идёт не о приобретающих в последнее время популярность оптических процессорах (являющихся, по сути, основанными на оптическом сигнале цифровыми процессорами) и не о достаточно подробно изученных специализиро- ванных оптических процессорах (применяемых, например, для спектральной обработки изображений), а именно об аналоговых АВМ, в которых воспроизводятся модели процессов, а рассматриваемой переменной величиной является, например, интенсивность светового потока или комплексная амплитуда одной из характеристик электромагнитного поля. Поскольку общая теория и приёмы построения и применения как специализированных, так и универсальных АВМ достаточно глубоко проработаны [9 -11] (ещё до массового распространения электронной вычислительной техники), при разработке оптических АВМ необходимо определить оптические способы реализации решающих блоков, выполняющих типовые операции.

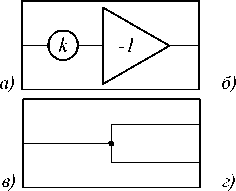
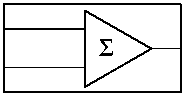
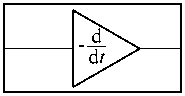
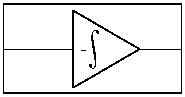
Базовыми линейными операциями являются: умножение на постоянный коэффициент, алгебраическое сложение, дифференцирование и интегрирование по времени (рис. 1). Для воспроизведения нелинейных зависимостей возможно либо использование специальных элементов, обладающих требуемыми нелинейными характеристиками, либо применение комбинаций типовых блоков и обратных связей.

д)

Рис. 1. Базовые операции АВМ: умножение на коэффициент (а), алгебраическое сложение (б), разделение сигнала (в), дифференцирование (г), интегрирование (д)

При разработке новых оптических АВМ потребуется найти ответ на следующие основные вопросы. Во-первых, какие оптические элементы и структуры могут быть использованы в качестве элементной базы оптических АВМ, какими характеристиками они могут обладать и как могут быть изготовлены? Во-вторых, в чём будет принципиальное отличие от уже существующих электрических АВМ, нишу решения каких задач смогут занять оптические АВМ?

шения совершенно другой задачи: сходные операции используются в телекоммуникационных приборах, применяемых в сетях цифровой волоконной связи. Бурное развитие телекоммуникаций привело к тому, что были разработаны лазеры, модуляторы, измерительные приборы, усилители сигналов и ряд других приборов и элементов [12, 13]. Поэтому многие современные исследования по оптическим АВМ используют виды волокон, источники излучения и измерительные приборы, изначально разработанные именно для телекоммуникационного применения.

Также большое влияние было оказано развитием цифровых оптических процессоров, поскольку в них тоже используются базовые, не зависящие от времени операции. Так, в работе [14] рассмотрен оптический процессор для умножения векторов и матриц, основанный на блоках разделения, объединения и усиления сигнала. Причём для оптических процессоров скорее характерно исполнение в виде интегральных оптических структур, т.е. реализованных на поверхности подложки в виде планарных оптических элементов и волноводов.

Суммирование оптических сигналов

Одной из базовых операций является сложение двух переменных величин, реализуемое для оптических сигналов путём их простого суммирования.

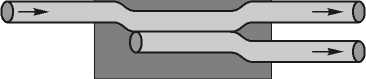
Суммирование оптических сигналов обычно производится с помощью буквального соединения волноводов, по которым распространяется излучение. В зависимости от вида волновода (планарного или оптического волокна) физическая реализация сумматора может отличаться, однако общая схема (рис. 2 а ) остаётся той же: волноводы либо объединяются в один, либо располагаются настолько близко друг к другу, что между распространяющимися в них пучками наблюдается взаимодействие [12]. В результате в выходном волноводе наблюдается сигнал, являющийся суммой двух исходных.

On тический сумм ат ор

Выход

Входы

а)

б)

Вход

Оптический разделитель

I^-~^“~| Выходы

Соединитель/разветвитель

Входы                    Выходы

о^ s------'   — (

в) U

Рис. 2. Общая схема оптического сумматора (а), разделителя (б) и соединителя/разветвителя общего вида (в)

Разделение оптического сигнала

На аналогичных эффектах основывается действие оптических разделителей (рис. 2 б ): подведённое по входному волноводу излучение возбуждает оба выходных волновода. В результате в выходных волноводах наблюдаются сигналы, сходные по характеристикам с исходным, но меньшей интенсивности.

Возможность оптического разделения сигнала позволяет реализовать ещё один фундаментальный элемент АВМ, – обратную связь: один из полученных после разделения сигналов может быть подведён по волноводу на вход блока, выполняющего более раннюю по порядку операцию. В этом случае время задержки будет определяться временем, за которое свет проходит образованный таким образом замкнутый контур волновода.

В общем случае возможно применение устройств, состоящих из нескольких оптических волокон, расположенных на определённом участке близко друг к другу или даже соединённых друг с другом (рис. 2 в ). Такие устройства называются оптическими разветвителями (optical splitters/couplers) [12].

Усиление оптического сигнала

Ещё одной базовой операцией является умножение переменной величины на заданное значение. Для оптического сигнала данная операция сводится к его ослаблению в случае умножения на величину менее единицы и к усилению в случае умножения на величину более единицы.

Для ослабления сигнала достаточно рассеять часть энергии или просто отвести часть энергии с помощью разделителя. Однако в силу невысокой энергетической эффективности операций дифференцирования и интегрирования более востребованным действием является, наоборот, усиление сигнала.

Усиление сигнала с заданными характеристиками может быть достигнуто путём применения оптических усилителей [15]. Широкое распространение получили усилители на основе оптического волокна, легированного ионами (doped fiber amplifiers, DFA). В них в качестве источника энергии выступает лазер, длина волны излучения которого отличается от длины волны основного используемого излучения. Лазер используется для возбуждения ионов в легированном участке волокна, которые потом излучают дополнительные фотоны под воздействием основного излучения. Наиболее широко применяются усилители на основе ионов эрбия (Erbium DFA, EDFA) [16- 17].

Также достаточно широко применяются полупроводниковые оптические усилители (semiconductor optical amplifiers, SOA) [18 - 20], сходные по строению с лазерными диодами. В них источником энергии является электрический ток, что, с одной стороны, уменьшает их размеры и делает их более дешёвыми, но, с другой стороны, такие усилители обладают худшими характеристиками по сравнению с EDFA.

2.    Реализация временных операций

Большой интерес представляют реализации зависящих от времени операций дифференцирования и интегрирования над переменными величинами, т.к. именно эти операции являются фундаментальной основой аналогового решения дифференциально-интегральных уравнений. Первые работы, посвящённые данной проблеме, появлялись значительно позже, чем работы, связанные с простыми операциями, причём по дифференцированию [21, 22] несколько раньше, чем по интегрированию [23 - 25], хотя интегрирование представляет намного больший интерес с точки зрения создания оптических АВМ. Существующие решения можно условно разделить на три группы по принципу их действия:

– основывающиеся на обратной связи и алгебраических аналогах операций,

– основывающиеся на характеристиках оптических структур в спектральной области,

– основывающиеся на характеристиках оптических структур во временнóй области.

Использование обратной связи и алгебраических аналогов операций

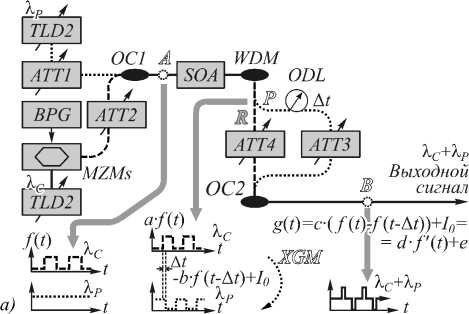
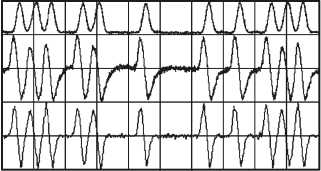
Первый подход опирается на интерпретации дифференцирования и интегрирования, характерные скорее для цифровой техники, чем для аналоговой. Так, в целом ряде работ [26-30] дифференцирование предлагается проводить путём разделения сигнала на два, введения временной задержки в канал одного из сигналов и последующего суммирования сигналов с весовыми коэффициентами. Таким образом, при правильном выборе коэффициентов получается аналоговый вариант конечной разности, являющейся приближением производной. На рис. 3 приведён пример схемы оптического дифференцирования, основанной на разделении сигнала и временной задержке, а также результаты оптического и численного дифференцирования гауссоподобного сигнала. Несложно убедиться, что наблюдается хорошее соответствие полученных результатов дифференцирования.

Аналогичный подход можно применить и для интегрирования, составив аналоговый вариант интегральной суммы (например, [23]). На рис. 4 приведена общая схема фильтра, использующегося при интегрировании по методу Ньютона-Котеса. Сигнал разделяется на заданное количество сигналов (определяется количеством членов в интегральной сумме), каждый из них в блоке TC умножается на постоянный коэффициент (определяемый весовым коэффициентом члена в ряде), затем в блоке PS обеспечивается временная задержка, после чего производится суммирование всех сигналов.

В целом, такой подход, основанный на алгебраических приближениях требуемых функций, с одной стороны, прост, т.к. базовыми элементами становятся разделители сигнала, временные задержки и усилители, но, с другой стороны, сам способ такого вычисления производных и интегралов уже содержит некоторую погрешность.

б)

Исходный сигнал Результат оптического дифференцирования

Результат численного дифференцирования

Рис. 3. Принцип действия и общая схема установки для оптического дифференцирования (TLD – настраиваемый лазерный диод, ATT – аттенюатор, BPG – генератор битов, MZM – модулятор Маха-Цандера, OC – оптическое соединение, SOA – полупроводниковый оптический усилитель, WDM – мультиплексор с разделением по длине волны, ODL – линия оптической задержки, XGM – перекрёстная модуляция) (а), результаты дифференцирования (б) (рисунок взят из работы [27])

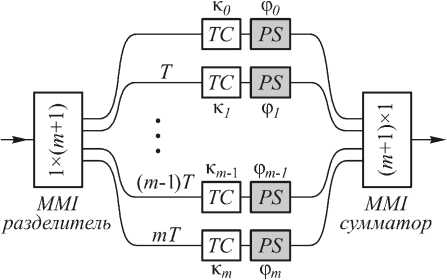
Рис. 4. Общая схема КИХ-фильтра, являющегося элементом интегрирующей схемы, основанной на применении формул Ньютона–Котеса (рисунок взят из работы [23])

Более того, величины применяющихся временных задержек имеют критическое влияние на характеристики элемента. В целом такие дифференцирующие устройства обладают низкой энергетической эффективностью (около 1%), высокой относительной ошибкой (порядка 10%), а успешно обрабатываемые сигналы могут иметь длительность порядка 100 пикосекунд. Для сравнения: электрические АВМ могли обрабатывать сигналы длительностью порядка микросекунд [9-11].

Впрочем, зарубежные работы основаны на применении простейших видов обратной связи, в то время как существуют подходы, позволяющие получить качественно лучшие результаты [31]. Определение возможности использования таких методик для оптического дифференцирования является одним из направлений развития оптических АВМ.

Использование сходства спектральной характеристики

Второй подход основывается на том, что некоторые оптические элементы при определённых условиях имеют спектральную характеристику (функцию пропускания), близкую к характеристике дифференцирующего и интегрирующего элемента. Правда, такой подход характерен скорее для дифференцирующих элементов, и в основном в публикациях рассматриваются следующие два вида элементов: микрокольцевой резонатор [32] и брэгговская решётка в оптическом волокне [33, 34]. В первых работах [22, 35] приводятся только теоретические обоснования и результаты численного моделирования (причём обычно не в рамках строгой электромагнитной теории), но после этого появляются работы, в которых проведён натурный оптический эксперимент с устройствами-прототипами [36-38]. Результаты этих экспериментов показывают, что энергетическая эффективность составляет порядка 3%, при этом достижима ошибка менее 1% (эти параметры естественным образом взаимосвязаны).

На рис. 5 показан микрокольцевой резонатор, выполненный в виде планарного оптического элемента.

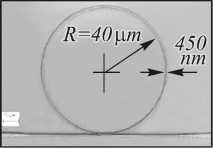
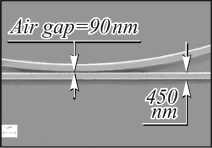
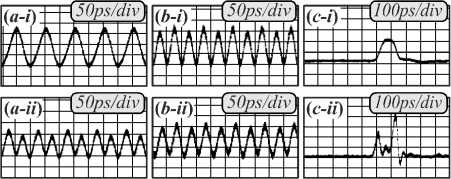
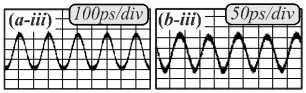
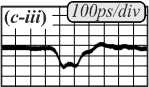
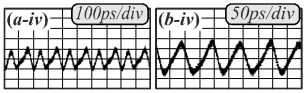
Рис. 5. Микрокольцевой резонатор (а) и его увеличенный фрагмент (б), результаты оптического дифференцирования (в) для разных видов сигнала: гауссоподобного (a-i, a-iii – входной сигнал; a-ii, a-iv – выходной сигнал), синусоидального (b-i, b-iii – входной сигнал; b-ii, b-iv – выходной сигнал) и импульсного (c-i, c-iii – входной сигнал; c-ii, c-iv – выходной сигнал) (ps – пикосекунды, div – деление на рисунке) (рисунок взят из работы [36])

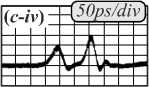
Входной сигнал подаётся в подходящий к резонатору волновод, выходной сигнал снимается из этого же волновода. Полученные в рамках натурного оптического эксперимента [36] результаты дифференцирования для различных видов входного сигнала качественно совпадают с искомой производной.

Особый интерес представляют решения на основе брэгговских решёток в волокне, т.к. они имеют больше параметров реализации, чем, например, мик-рокольцевой резонатор, и путём их варьирования можно добиться принципиально иных результатов. Так, целый ряд работ [22, 37 -40] посвящены тому, как путём изменения структуры решётки можно добиться более высоких точности и эффективности выполнения операции. Более того, предлагаются решения, когда элемент выполняет сразу вычисление производной заданного чётного порядка, и это решение оказывается намного более выгодным с энергетической точки зрения, чем применение последовательности дифференциаторов первого порядка [40].

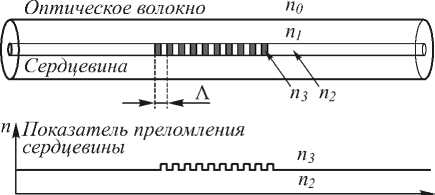
На рис. 6 а представлена общая структура волоконной брэгговской решётки. В случае решёток с регулярной структурой и решёток со сдвигом фазы (достигается с помощью нечётного числа неоднородностей решётки) спектральная характеристика, соответственно, в режиме пропускания и в режиме отражения будет в значительной мере совпадать с характеристикой операции дифференцирования. На рис. 6 б приведена интенсивность входного сигнала, а на рис. 6 в – квадрат значения производной, полученный в результате прохождения через волоконную брэгговскую решётку (сплошная линия) и в результате численного дифференцирования исходного сигнала (пунктирная линия) [39]. Точность дифференцирования, как нетрудно заметить, оказывается достаточно высокой.

Особый интерес представляет создание дифракционных оптических элементов (ДОЭ), спектральная характеристика которых обладает требуемыми свойствами. Преимущество такого подхода заключается в том, что дифференцирование производится с помощью ДОЭ, работающего в режиме пропускания, причём без формирования задержек и использования обратных связей. Первые результаты [41 - 42], полученные с помощью численного моделирования, показывают хорошие перспективы предлагаемого решения.

Формирование сигнала во временной области

Третий подход характерен в основном для интегрирующих устройств и основан на формировании сигнала во временнóй области. Для этого, опять же, в основном применяются микрокольцевые резонаторы и брэгговские решётки в волокне, но в несколько иных режимах использования, чем в случае дифференцирования. В целом, резонатор используется для многократной задержки в нём сигнала с последующим суммированием с текущим сигналом, что в сочетании с резонансными эффектами и приводит к интегрированию.

Интенсивность, отн.ед.

1,0

0,8

0,6

0,4

0,2

Время, нс

б) 0         1        2        3        4        5

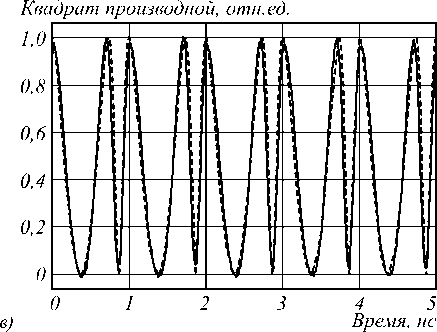
Рис. 6. Общая структура волоконной брэгговской решётки (а), интенсивность входного сигнала (б) и квадрат производной (в) по данным оптического (сплошная линия) и численного (пунктирная линия) экспериментов (рисунок взят из работы [39])

Основной проблемой при таком подходе является то, что окно интегрирования имеет конечную ширину, что приводит к ограничению длины корректно обрабатываемого сигнала. В целом достижимы ширина окна интегрирования порядка сотен пикосекунд, энергетическая эффективность порядка 10%, разрешающая способность по длительности сигнала порядка 10 пикосекунд, а возможная ошибка порядка 1%.

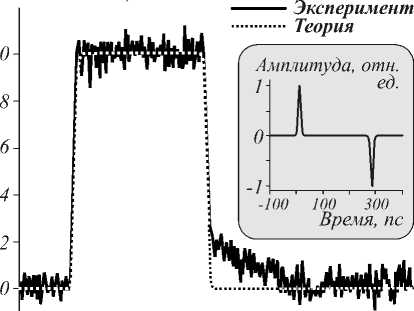
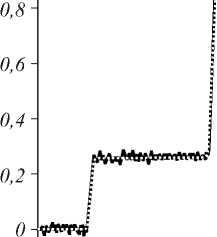
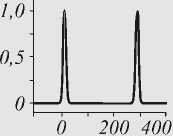
Использование микрокольцевых резонаторов для интегрирования [32, 35, 43, 44] несколько отличается от их использования для дифференцирования (рис. 7): выходной сигнал обычно снимается не из того же волновода, по которому подаётся входной, а из дополнительного. На рис. 8 а-г приведено сравнение результатов численного и оптического интегрирования сигналов для различных видов сигналов [43].

Транзит

Входной сигнал х<^

Ввод

Добавка

/ПЛи Выходной сигнал Вы^ У<Йд^

Рис. 7. Общий принцип интегрирования с помощью микрокольцевого резонатора (рисунок взят из работы [43])

Интенсивность, отн.ед.

Амплитуда, отн.ед.

Интенсивн., отн.ед.

О ' 100

Время, нс

-100      300

Время, пс

----Эксперимент .............. Теория

200    400    600     800

а)                                       Время, не

Интенсивность, отн.ед.

б)

Интенсивность, отн.ед.

Ж) '   400   '   600

Время, пс

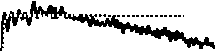
Амплитуда, отн.ед.

Время, пс

---Эксперимент

....... Теория

~О    ' 200 ' 400 ' 600

в)                                      Время, пс

Интенсивность, отн.ед.

од-

од-

---Эксперимент

....... Теория

WW^

Амплитуда, отн.ед.

ДЖИМ ^1140 пс

-4 -2 0 2 4 Время, нс

0,6 ОД То Т? 1,4 г)                                      Время, нс

Рис. 8. Сравнение результатов численного и оптического экспериментов для различных видов сигнала (а-г) (рисунки взяты из работы [43])

Анализ результатов показывает, что достигается достаточно высокая точность интегрирования, однако она стремительно падает при выходе за пределы окна интегрирования.

Аналогично, для интегрирования используются волоконные брэгговские решётки [24, 25, 45 - 50]. При прохождении через решётку свет испытывает множественные переотражения на внутренних поверхностях участков с изменённым показателем преломления. Это позволяет получать на выходе такого волокна не только сам сигнал, но и его повторения, характеристики которых определяются свойствами решётки. При этом решётки с регулярной структурой используются в режиме отражения [25], а решётки с фазовым сдвигом – в режиме пропускания [24].

Общая схема интегратора показана на рис. 9 а .

б)

Вход xW

980/1550 соединитель

(1) Двойной входной импульс

Цыънооптический интегратор i Выход XO=f .r(t)dT

IIMIIIIIIIIIIIIIIIIIIIIIIIIIII

_ __ волокно с брэгговскими структурами

а) Накачка

(2) Интегриро- (3) Интегриро вание ля не- впадающей фазы)

совпадающей фазы)

'ля со- ванне

170 пс

500 пс

1000 нс

Время, нс

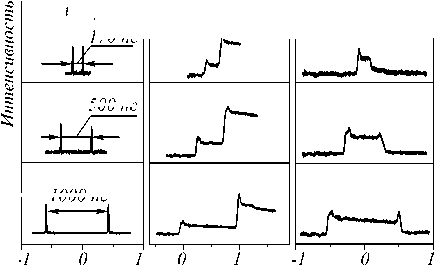
Рис. 9. Общая схема интегратора на основе брэгговской решётки (а) результат интегрирования для двух импульсов (б) (рисунок взят из работы [47])

На рис. 9 б приведены полученные в ходе натурного оптического эксперимента [47] результаты интегрирования входного сигнала, сформированного из двух отдельных импульсов. Результаты демонстрируют качественное совпадение с искомой функцией интеграла, при этом также наблюдается влияние конечного окна интегрирования на результат.

Варьирование параметров решётки позволяет получать более высокую точность и энергетическую эффективность интегрирования [49], а также вычислять интегралы чётного порядка без применения повторного интегрирования [46]. Также рассмотрены способы увеличения ширины окна интегрирования, вплоть длительности порядка сотен пикосекунд [50].

3.    Решение дифференциальных уравнений

Несмотря на достаточную сложность реализации, рассмотренные операции дифференцирования и интегрирования являются лишь элементами при построении более сложных устройств, нацеленных на решение дифференциальных уравнений.

В работе [47] приводится уже не просто расчёт характеристик оптического элемента и результаты его работы на тестовых сигналах, но пример и результаты оптического эксперимента по решению обыкновенного дифференциального уравнения первого порядка. На рис. 10 приведена постановка задачи решения дифференциального уравнения первого порядка, а также результаты оптического эксперимента (непрерывные графики) в сравнении с результатами численного решения (точки решений отмечены кружками). Совпадение оптического и численного решений подтверждает возможность и актуальность создания оптических АВМ нового поколения.

Заключение

Возвращаясь к вопросам, поставленным в начале, можно сказать следующее. В основу элементной базы оптических АВМ могут лечь оптические элементы, обладающие резонансными свойствами: брэгговские решётки, микрокольцевые резонаторы и ДОЭ, причём обеспечение высокой точности работы элементов потребует высокого качества их реализации и применения лазеров с настраиваемой длиной волны. По сравнению же с электрическими АВМ оптические АВМ будут обладать высокой скоростью реакции и разрешающей способностью (порядка 10 пикосекунд против микросекунд), компактностью и возможностью интеграции в системы сбора и передачи информации на основе оптических волокон.

В качестве возможных направлений работ следует рассмотреть следующие:

• –    определение возможности применения схем с обратной связью, а также различных резонансных структур и дифракционных оптических элементов для дифференцирования/интегрирования оптического сигнала (на основе моделирования в рамках строгой электромагнитной теории);

  Оператор интегрирования	-y(0— | R ) | —- v(O=Jx(T)dT
  Дифференциальное уравнение первого порядка	^Т^+к^СО^СО
  Реализация	xU) з         К ‘          * —®*[foP*-v И =J_r (^т-к£у( Т )dr

б)

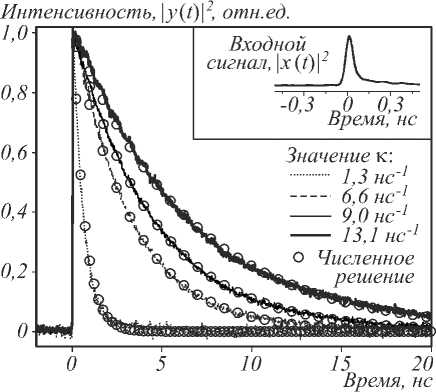
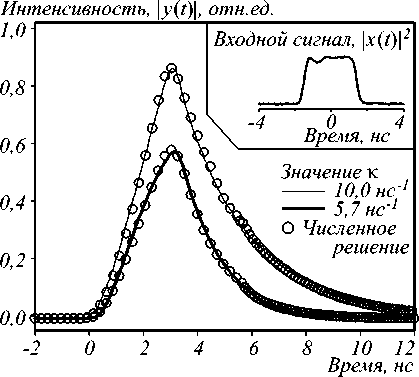
Рис. 10. Пример решения дифференциального уравнения: постановка задачи (а), решения для двух видов входного сигнала и различных значений параметра уравнения (б, в)

(рисунок взят из работы [47])

• –    определение на основе моделирования характеристик выполнения операций и условий применимости оптических элементов (точности выполнения, энергетической эффективности, допустимых диапазонов длин волн и т.д.);

• –    определение зависимости характеристик выполнения операций от качества реализации оптических структур (также на основе моделирования);

• –    создание прототипов оптических элементов, выполняющих дифференцирование и интегрирование оптического сигнала (с учётом рекомендаций, полученных на предыдущих этапах);

  – разработка рекомендаций относительно возможных реализаций АВМ с учётом характеристик элементной базы.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы» (Государственный контракт №07.514.11.4055), а также грантов РФФИ (гранты №10-07-00438-а, №10-07-00553-а) и грантов Президента Российской Федерации НШ – 4128.2012.9, № МД - 1041.2011.2.