Первая собственная частота плоской правильной фермы. Аналитическое решение

• 1    Введение / Introduction

  Развитие методов аналитического расчета конструкций в 2000–2020 гг. Например, увеличение мощности вычислительной технике, позволило решать численными методами нелинейные дифференциальные уравнения прогиба упругих конструкции без разбиения ее на простые части или реализовывать алгоритмы поиска собственных частот методом индукции. Это позволило создать альтернативу численным расчетам, основанным, как правило на методе конечных элементов [1]. В [2] для получения аналитических решений использовался метод разложения решений в ряды. Отдельно можно выделить расчеты регулярных систем, для которых методом индукции выводятся формулы зависимости прогиба конструкций или частоты колебаний от порядка системы. В [3] предложена стержневая модель статически определимой плоской рамы с четырьмя опорами. Решена задача получения аналитической зависимости прогиба фермы под действием различных нагрузок от количества панелей в ригеле. Для решения задачи используется система компьютерной математики Maple ( www.maplesoft.com ). Система уравнений равновесия узлов фермы решается в символьной форме. Показано, что при определенном количестве панелей в ригеле определитель системы уравнений равновесия обращается в нуль, что свидетельствует о кинематической изменчивости конструкции. В [4] рассмотрена новая схема статически определимой пространственной фермы шестигранного купола. Выведены формулы для прогиба вершины и углового шарнира в зависимости от порядка регулярности конструкции. Найдены верхняя и нижняя аналитические оценки первой частоты собственных колебаний конструкции. Найдены асимптотики решений. Колебания пространственной консольной статически определимой фермы, состоящая из трех плоских ферм с треугольной решеткой рассмотрены в [5]. Проанализирован спектр собственных частот конструкции. В аналитической форме решена задача нахождения зависимости низшей частоты колебаний фермы от количества панелей, массы, линейных размеров конструкции и свойств материала. Использован подход Донкерлея. Показано существование спектральных изолиний, обладающих свойством асимптотического стремлению к некоторой постоянной величине. Объектом исследования [6] является пространственная статически определимая ферма

покрытия пирамидального типа. Разыскивается аналитическая зависимость прогиба конструкции от количества панелей в ее основании. Обобщение частных решений на произвольное число панелей получается по индукции с использованием операторов системы компьютерной математики Maple. Выбор этой системы произволен. С не меньшим успехом расчеты возможны и в системах Mathematica, Derive, Reduce и др. Большая же часть упомянутых выше работ (за исключением [1]) выполнены в системе Maple, имеющей специальные операторы для индуктивного обобщения расчетов регулярных систем на произвольное число панелей. В [7] исследуется статически определимая плоская регулярная ферма с параллельными поясами. Приведен вывод формулы зависимости первой частоты собственных колебаний фермы от числа панелей и жесткости одного из опорных звеньев. Формула для прогиба плоской статически определимой решетчатой фермы на двух опорах в зависимости от числа панелей получена в [8]. Верхний пояс сооружения имеет треугольное очертание. Для получения значения прогиба используется формула Максвелла – Мора. В [9] формула зависимости прогиба от числа панелей статически определимой фермы рамного типа выводится методом индукции. Рассмотрена равномерная и сосредоточенная нагрузка на верхний пояс. Приведена картина распределения усилий по стержням фермы. Методом Донкерлея найдена аналитическая оценка снизу первой частоты колебаний в предположении, что масса фермы равномерно распределена по узлам. Отмечается высокая точность полученной оценки, растущая с увеличением числа панелей. Кроме этого, в множестве спектров регулярных ферм различного порядка обнаружены спектральные изолинии и спектральные константы. Аналитический расчет прогиба конструкции, представляющей собой П-образную раму, сочлененную в середине пролета, выполнен в [10] с помощью операторов системы Maple. Ряд решений, полученных для конструкций с различным числом панелей, обобщается методом индукции на произвольный порядок фермы. Усилия в элементах статически определимой конструкции вычисляются в символьной форме методом вырезания узлов. Для расчета прогибов применяется интеграл Мора. Рассмотрены четыре варианта нагрузок. Обнаружены асимптотики решений. Объектом исследования в [11] является статически определимая плоская ферма с двумя пролетами и ромбовидной решеткой. Одна из опор — это неподвижный шарнир, две других опоры — подвижные. Зависимость первой собственной частоты колебаний фермы от ее размеров, массы, а также количества панелей находится в простом аналитическом виде. Жесткость конструкции с массами, сосредоточенными в ее узлах, определяется по формуле Максвелла-Мора. Нижняя аналитическая оценка первой частоты вычисляется по приближенной формуле Донкерлея с учетом только вертикальных смещений масс. Сравнение аналитического решения с численным показывает, что точность аналитической оценки снизу достаточно высока и увеличивается с ростом числа панелей. Нижняя граница первой частоты колебаний плоской фермы Финка получена в [12] по данным о парциальных частотах конструкции. Двухсторонняя оценка первой частоты колебаний фермы в аналитическом виде для произвольного числа панелей найдена в [13]. Верхняя граница в этой работе рассчитана по методу Рэлея. Деформационный расчет регулярной пространственной конструкции покрытия прямоугольной формы в аналитической форме выполнен в [14]. В [15] изучена пространственная схема купольной конструкции. Нижняя аналитическая оценка первой частоты получается по методу Донкерлея. Верхняя оценка первой частоты находиться энергетическим методом Рэлея. Собственные колебания статически определимой плоской фермы балочного типа с тройной решеткой с короткими нисходящими и длинными восходящими связями рассмотрены в [16]. Масса фермы моделируется сосредоточенными нагрузками в ее узлах. Для первой собственной частоты методом Донкерлея выводится формула зависимости ее нижней границы от числа панелей. Показано, что при определенном количестве панелей предлагаемая схема фермы обладает свойством кинематической изменяемости. В частотном спектре семейства ферм различного порядка обнаружены спектральные константы. В [17] предложена и рассчитана схема статически определимой фермы башенного типа. Выведена формула зависимости первой частоты собственных колебаний от размеров конструкции и ее порядка регулярности. Проанализирован спектр собственных частот фермы. В наборе спектров семейства регулярных ферм различного порядка найдены спектральные изолинии и константы. Тиньков Д.В. [18] вывел точные аналитические выражения для оптимальной геометрии и минимальной массы диагональной ферменной балки из материала со свойствами линейной ползучести. Получены простые аналитические выражения для прогиба оптимального веса фермы. Исследование проводилось в системе Maple в символьной форме. Для сравнения и проверки решений использовался многофункциональный программный комплекс «Лира» (lira- Maslov, A.

The first natural frequency of a planar regular truss. Analytical solution;

soft.com), предназначенный для проектирования и численного расчета зданий и инженерных сооружений. В [19] предложен и реализован применительно к плоской ферме упрощенный метод получения верхней оценки первой частоты собственных колебаний на основе метода Рэлея. Варианты метода Донкерлея для оценки первой частоты снизу рассмотрены в [19]–[21]. Впервые проблемой существования регулярных стержневых структур заинтересовались Hutchinson R.G. и Fleck N.A. [22],[23]. Большой вклад в теорию регулярных ферм, их классификацию и проблему оптимизации таких конструкций внес Kaveh A. [24],[25]. В [2] в системе компьютерной математики Maple получено аналитическое решение краевой задачи для системы дифференциальных уравнений в перемещениях, описывающей деформацию прямоугольной пластины, опирающейся на ребра жесткости. Решение представлено в виде рядов с комбинацией регулярных и специальных сингулярных функций, которые быстро сходятся и приводят к простому вычислительному алгоритму, реализовать который можно и в символьной форме. В справочниках [27],[28] собраны схемы и формулы для прогибов различных плоских регулярных статически определимых ферм с произвольным числом панелей.

Несмотря на многочисленные численные и аналитические методы решения задач о деформациях и собственных частотах колебаний стержневых систем, описанные выше, здесь остается еще одна достаточно важная проблема. Это проблема исследований регулярных конструкций большого порядка. Численный расчет систем с числом стержней (панелей), превышающим некоторое вполне реальное на практике значение, начинает сталкиваться с непреодолимым проклятием размерности, связанным с неизбежным накоплением ошибок округления и объемом вычислений. Аналитический метод с использованием индукции, хорошо справляется с этим недостатком численных расчетов, но при этом зачастую расчетные формулы получаются весьма громоздкими и неудобными на практике. Особенно это касается верхней оценки первой частоты методом Рэлея.

В настоящей работе предлагается новый подход вычисления приближенного значения первой частоты на основе метода Рэлея, дающий компактную и точную оценку решения. Для примера рассматривается простая балочная ферма с параллельными поясами.

• 2    Материалы и методы / Materials and Methods

  2.1    Схема фермы

Рассматривается плоская регулярная ферма балочного типа высотой h и длиной пролета 2 na (рис. 1). Число панелей равно n . Каждая панель фермы состоит из двух стержней верхнего пояса, средней стойки и двух раскосов. Панели соединяются по нижнему поясу двумя стержнями с дополнительной вертикальной стойкой. Ферма статически определимая, симметричная.

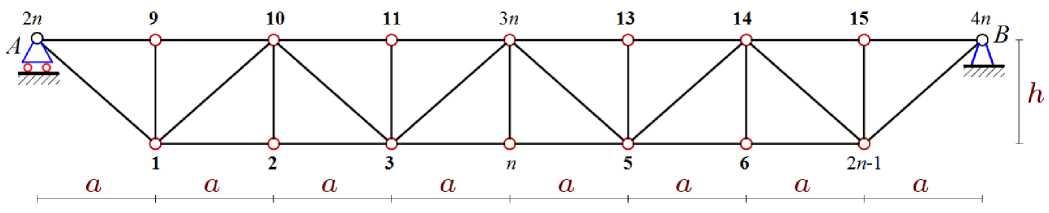
Рис. 1 – Схема фермы, n =4

Fig. 1 – The truss scheme, n =4

Конструкция фермы состоит из N = 8 n стержней. В это число входят и три стержня, представляющие опоры. Масса фермы моделируется K = 4 n + 2 сосредоточенными массами, распределенными по ее узлам. Принимается, что массы колеблются только по вертикали. Отсюда число степеней свободы рассматриваемой модели фермы равно K . Жесткость конструкции определяется по формуле Максвелла – Мора. Усилия, входящее в сумму Максвелла – Мора, определяются в аналитической форме методом вырезания узлов с использованием программы, составленной на языке символьной математики Maple. Для этого узлы нумеруются и задаются их координаты. Начало координат располагается в левой подвижной опоре:

xi = ai,yi = 0, i = 1,..2n -1, xi+2n-i = a(i- 1), У++2n-i = h, i = 1,-.2n +1

Структура решетки определяется списками концов стержней. Верхний пояс, например, задается следующими списками: Ф i _{+ 2 n — 2} = [ i + 2 n - 1, i + 2 n ], i = 1,..,2 n.

2.2    Численный расчет частот колебаний фермы

Матричная форма динамических уравнений системы масс в узлах фермы записываются в виде:

m I K Y + D K Y = 0                                     (1)

Вектор вертикальных смещений масс в узлах фермы обозначен как Y , Y — соответствующий вектор ускорений, I K — единичная матрица размера K х K , D K — матрица жесткости. Обратной к матрице жесткости D _K является матрица податливости B _K , которая вычисляется по формуле Максвелла – Мора:

N b,,, =YS"Sa')l. /(EF).                                         (2)

a= 1

Обозначено: b ij — перемещение узла с номером i от действия единичной вертикальной безразмерной силы, приложенной к узлу j , S ^ i ’ — усилия в стержне а от действия единичной вертикальной силы, приложенной к узлу i , в котором находится масса m , l _а - длина стержня с номером а , EF — жесткость стержней.

Так как при гармонических колебаниях с частотой о справедлива связь смещений и ускорений вида Y = -о ² Y , то умножением уравнения (1) слева на матрицу податливости, задача приводится к стандартной проблеме собственных чисел матрицы B K : B K Y = 1 Y , где 1 = 1/ ( о ² m ) — собственное число матрицы B K , о — собственная частота колебаний. Отсюда связь собственной частоты колебаний и собственного числа матрицы B K : о = 4 1/( m 1 ) .

В общем случае задача на собственные частоты системы с многими степенями свободы можно получить лишь численно. Однако известны два метода, позволяющие найти верхнюю и нижнюю границу первой частоты в аналитической форме. Это метод Донкерлея для оценки снизу и метод Рэлея для оценки сверху.

2.3    Оценка первой частоты по Донкерлею

Формула Донкерлея для оценки первой частоты снизу имеет вид:

K

—2

оD = X оp , p=1

где о p — парциальные частоты, которые определяются из уравнений движения отдельных масс в узлах:

myp + dpyp = 0, p = 1,2,...,K.

Скалярный коэффициент жесткости d_p , обратный коэффициенту податливости, вычисляется по формуле Максвелла – Мора, используемой при расчете перемещений узлов ферм:

A z ..2

⁵ p = 1/ d p = X ( S ! ^p ’ ) ‘ j /(EF ) = U p /( h ² EF )•                              (5)

J = 1

Для гармонических колебаний по форме У р = A p sin( w p t + ф ) из (3) и (4) следует выражение для парциальной частоты Ю р = ^ d p / m . Отсюда:

KK

® d = m Е д _р = m Е u_p / ( h 2 EF ) = mU n / ( h 2 EF ).

p = 1         p = 1

K

Здесь введено обозначение: U n = Е u_p . Расчет серии ферм с разным числом панелей p = 1

дает следующую последовательность сумм в (6):

U 1 = a ³ + c ³ + 4 h 3 ,

U 2 = 13 a ³ + 5 c ³ + 17 h 3 /2,

U ₃ = 553 a ³/9 + 35 c 3 /3 + 118 h ³ / 9, U ₄ = 189 a ³ + 21 c ³ + 71 h ³/4,...

где c = a a ² + h ². Серию решений (7) можно обобщить в виде

U = Ca ³ ₊ Cc ³ ₊ Ch 3 .

n 123

Чтобы определить три коэффициента в (8) серию (7) надо продлить по крайней мере до десяти выражений и получить общие члены последовательностей из решение рекуррентных уравнение в системе Maple:

C 1 = (2 n + 1)(2 n - 1)(8 n ² + 7) / 45,

C ₂ = (4 n ² - 1) / 3, C 3 = (14 n ² - 3 n + 1) /(3 n ).

Для оператора rgf_findrecur системы Maple, генерирующего рекуррентное уравнение для членов последовательности, требует последовательность четной длины. Коэффициенты (9) находятся из решения рекуррентных уравнений с помощью оператора rsolve. Альтернативный путь обобщения серии решений на общий случай предоставляет пакет компьютерной математики Mathematica [29]. В результате формула для нижней оценки первой частоты собственных колебаний фермы по Донкерлею имеет вид

' = ^h

EF

2.4    Расчет первой частоты колебаний по Рэлею

В [4,15] энергетическим методом Рэлея получено приближенное выражение для первой частоты колебаний фермы (оценка сверху):

KK ю2 = У U / У mu,2 Ri  i

N

где йi =ЕS^aP)Sii)la /(EF) — вертикальное смещение узла i от действия единичной a=1

распределенной узловой нагрузки по всем узлам фермы, в которых расположены массы. В результате расчета ферм с последовательно увеличивающимся числом панелей получены следующие выражения в числителе (11):

n = 1: £ u = (2 a ³ + 2 c ³ + 9 h ³) / (EFh ² ), i =1

n = 2 : ^ u i = (136 a ³ + ⁴° c ³ + 7° h ³) / (EFh ² ), i =1

n = 3 : £ U i = (1554 a ³ + 21° c ³ + 231 h ³) / (EFh ²), i =1

n = 4 : £e = (8736 a ³ + 672 c ³ + 54° h ³) / (EFh ² ), i =1

n = 5 : £ U i = (3333° a ³ + 165° c ³ + 1°45 h³) / (EFh ² ),... i =1

Обобщение этих результатов на произвольное число панелей n дает следующую формулу: K

£ й = (Ca " + C 2 C ³ + C 3 h ") / (EFh ²), i =1

где коэффициенты находятся как решения линейных рекуррентных уравнений:

C 1 = 2n²(16n ⁴ - 1)/15,

C ₂ = 2n ²(4 n ² - 1)/3,                                       (12)

C ₃ = n (2n + 1)(4 n — 1).

Аналогично получается выражение для знаменателя

£mU 2 = m ( С 4 a ⁶ + С 5 c ⁶ + С 6 h ⁶ + С 7 a³ c ³ + С 8 a ³ h ³ + С 9 h ³ c 3 )/ ( EFh ²)², i = 1

где

C 4 = 2 n ² (4 n ² - 1)(496 n ⁶ + 328 n ⁴ + 103 n ² + 18)/ 2835,

C 5 = 2 n ²(16 n ⁴ - 1)/15,

C 6 = n (2 n + 1)(8 n ² - 1),

C 7 = 4 n ² (4 n ² - 1)(68 n ⁴ + 31 n ² + 6) / 315,

C 8 = 2 n ² (16 n ⁴ - 1)(4 n + 1)/15,

C 9 = 2 n ²(4 n ² - 1)(4 n + 1)/3.

2.5    Упрощенный вариант расчета первой частоты по Рэлею

В методе Рэлея наибольшую сложность вызывает получение формулы для знаменателя (11). Кроме того, результат получается в виде громоздких формул для шести коэффициентов (12). В [19] предложен упрощенный способ вычисления знаменателя (11).

K

£ mu² = Km a max /2.

i = 1

Такое упрощение имеет смысл только для аналитического решения, получение которого связанно с суммированием, а затем поиском общего члена последовательностей полученных сумм. Единственная сложность в упрощенном решении (14) — это выбор узла i , для которого коэффициент u максимальный. В данной ферме это узлы с номерами n или 3 n в серединах поясов. Для получения зависимости прогиба в середине нижнего пояса от действия распределенной единичной нагрузки требуется выписать 12 последовательных выражений:

n = 1: umax = (a3 + 2h3 + c3)/(EFh2), n = 2: umax = (14a3 + 5h3 + 4c3)/(EFh2), n = 3: umax = (69a3 + 6h3 + 9c3)/(EFh2), n = 4: umax = (216a3 + 9h3 +16c3)/(EFh2), n = 12: umax = (17304a3 + 25h3 +144c3)/(EFh2).

Рекуррентное уравнение для членов этой последовательности имеет вид u„ = 4 u„ - 5 u„ -> + 5 u„ л — 4 u„ +u u„ _A.

n        n - 1         n - 2        n - 4         n - 5       n - 6

Решение этого уравнения имеет вид umax = (5 a3 n4 + (a3 + 6 c3) n2 + 3 h 3(4 n + (-1)n +1))/(6 EFh2).                      (15)

Таким образом, предлагаемое упрощенное решение по Рэлею имеет вид

72( C 1 a ³ + C₂c ³ + C ₃ h³)EF / (mn ) ^R' ~     5a³n ⁴ + (a ³ + 6 c ³) n ² + 3h ³(4 n + (-1) " + 1)^,

где коэффициенты в числителе рассчитываются по формулам (12).

• 3    Результаты и их обсуждение / Results and Discussion

Для оценки точности рассмотренных аналитических методов можно использовать численное решение, полученное для первой частоты спектра частот собственных колебаний фермы. Длина панели фермы: a = 2м, высота h = 3м. Площадь поперечных сечений стержней решетки и опорных стержней: F = 7 см² . Массы в узлах m = 400кг , модуль упругости материала стальных стержней E = 2,1 - 10 5 MПa. На графике 2 приведены зависимость первой частоты го D от числа панелей, вычисленной по формуле Донкерлея (10) с коэффициентами (9), частоты ^ R по формуле Рэлея (11) с коэффициентами (12) и (13), частоты го R , по упрощенной формуле Рэлея (16) и найденная численное значение первой частоты го 1 из спектра системы с K степенями свободы. Кривые ^ R и го 1 практически сливаются, демонстрируя высокую точность метода Рэлея.

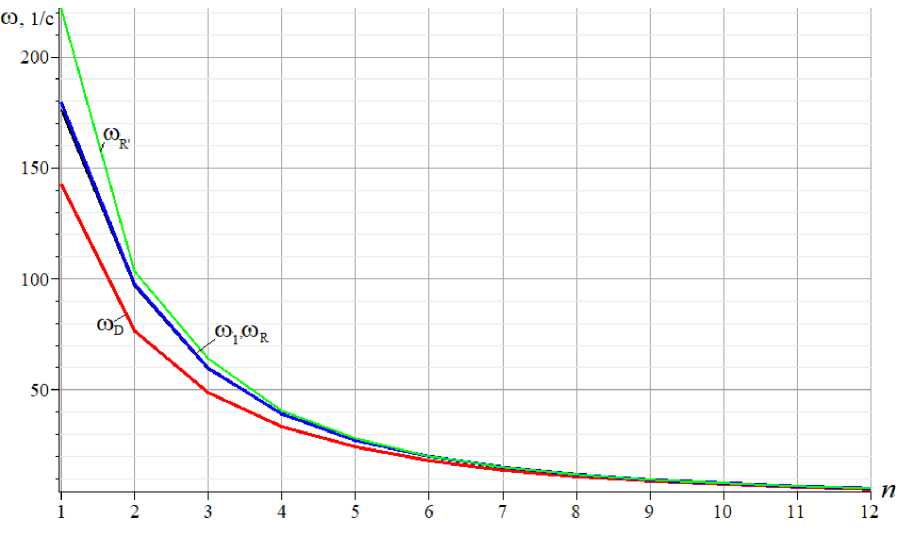
Рис. 2 – Зависимость от числа панелей первой частоты колебаний по четырем методам

Fig. 2 – Dependence on the number of panels of the first oscillation frequency by four methods

Сравнить точность методов можно по относительным величинам £ D = | го D -го ₁ |/ го ₁ ,

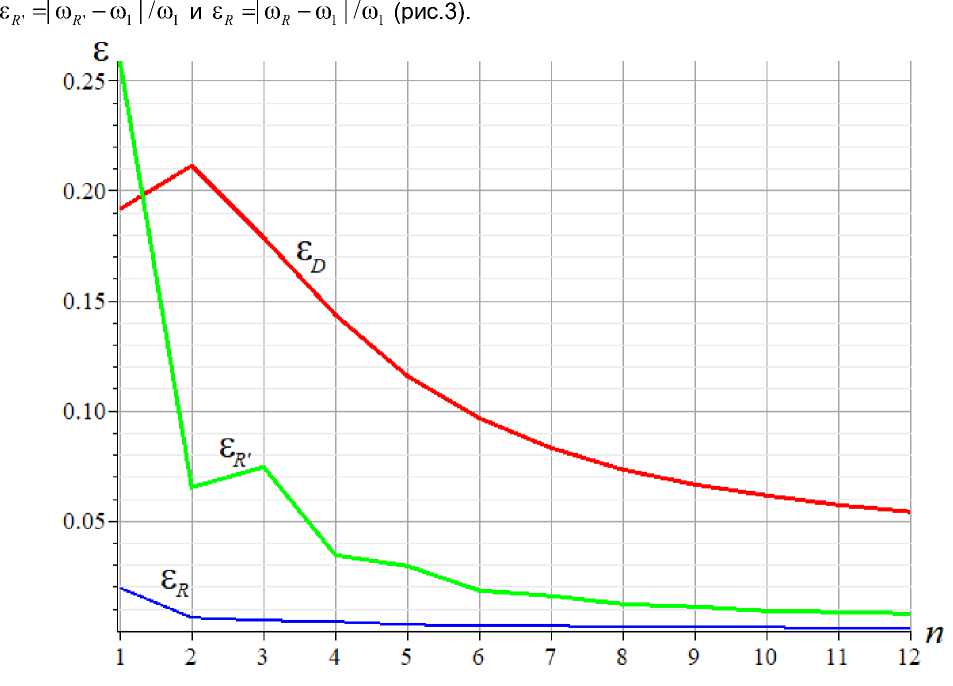
Рис. 3 – Сравнительная погрешность методов

Fig. 3 – Comparative error of methods

С увеличением порядка фермы, начиная с некоторого значения n , погрешность всех трех методов уменьшается. При этом упрощенный метод Рэлея дающий сравнительно компактную расчетную формулу, имеет точность в несколько раз большую, чем метод Донкерлея. Предлагаемый вариант метода Рэлея лучше всего подходит для оценки в аналитической форме первой частоты колебаний ферм с большим количеством панелей.

Следует отметить, что рассмотренные методы касаются только аналитических исследований собственных частот в символьной форме. Использовать эти подходы в случае численного расчета первой частоты нет смысла. Этой проблемой хорошо справляются практически любые специализированные пакеты с использованием метода конечных элементов. Аналитические же решения хорошо дополняют численные и могут быть использованы для простой оценки и тестирования численных результатов.

• 4    Выводы/ Conclusions

Основные результаты работы:

• 1.    Рассмотрены три аналитические метода для нахождения оценок сверху и снизу первой частоты колебаний регулярной фермы с многими степенями свободы. Результат имеет форму простых формул с погрешностью в несколько процентов.

• 2.    На примере расчета частот простой балочной фермы показано, что погрешность упрощенного метода Рэлея, заметно меньше, чем погрешность метода Донкерлея и уменьшается с увеличением числа панелей. Однако по форме решение метода Донкерлея более компактное.