Первопринципные расчеты энергии смешения и магнитных моментов компонентов сплавов Fe-Mn, Fe-Cr и Fe-Ni-C ОЦК и ГЦК решетками

Важной и актуальной задачей физики твердого тела является расчет энергии взаимодействия атомов в твердом растворе. В последние годы появились пакеты компьютерных программ, позволяющие с большой точностью рассчитывать полную энергию вещества на основе метода функционала электронной плотности. В настоящее время наличие быстродействующих компьютеров дает возможность расчета свойств твердого раствора замещения методом суперячейки [1]. В этом методе самосогласованный зонный расчет электронной структуры проводится для модельного кристалла, образованного периодически повторяющейся в пространстве элементарной ячейкой, в качестве которой берется определенная часть исследуемого неупорядоченного мате риала.

Отметим, что сходную величину измеряют или рассчитывают косвенными методами в термохимии [2]. Речь идет об энергии (теплоте) смешения компонентов в растворе Е^ , которая для бинарного раствора при Т = const представляет разность между энергией (энтальпией) раствора и энергиями чистых компонентов В и С, взятых в соответствующих пропорциях. В простейшем квазихимическом приближении

^см " ^МСс ’                                (О где A = ^zN^8bc-8cc-sbb^

представляет энергию взаимообмена атомов сорта В и С. Таким образом, теплота смешения прямо выражается через энергии взаимодействия 8ц атомов сорта / и j. Если принять, что изменение энтропии при растворении сводится к конфигурационной энтропии для неупорядоченного распределения атомов, то получается так называемая модель регулярных растворов [3]. В этом случае параметр А не должен зависеть от концентрации, но может изменяться при варьировании температуры. В следующем приближении используется модель субрегулярных растворов, согласно которой А = Avxa + А2хв.

Экспериментальные измерения теплот смешения или параметров А проводят методами давления насыщенных паров, электрохимическим и калориметрическим методами [2], но для ограниченных растворов и тем более неравновесных фаз параметр А может быть грубо оценен только на основе граничных концентраций фаз, находящихся в стабильном или метастабильном равновесии. Но даже в том случае, когда проводятся измерения, они относятся к высоким температурам, а экстраполяция экспериментальных результатов в область низких температур всегда сопряжена с риском ошибки.

2.    Сплавы Fe-Mn

В таблице приведены данные о термодинамических параметрах А“ и А⁷ для 7- и «-твердых растворов марганца в железе по различным литературным источникам. Здесь               ■

______ хАхв хАхв хАхв где МЗизб есть избыточная величина свободной энергии смешения по отношению к идеальному раствору. В этом уравнении не зависящий от температуры член соответствует энергии смешения, а коэффициент при Т выражается через избыточную энтропию смешения, которая часто оказывается независящей от температуры.

Термодинамические функции сплавов Fe-Mn

№ п.п.	А7, Дж/моль	А“ , Дж/моль	E°G^7 , Дж/моль	Лит. источник
1	+4960	+480		[3]
2	-21800 + 19,087	-3370-16,43 7- 1500 Sm	-1800 + 1,276 7	[4]
3	730-107	19 450 —12,81 7— 1500 Sm	-1800 + 1,276 7	[5]
4	-18 870 + 16,987 7	4100 xFe + 5188 xMn + (4,486 xFe + l,506xMn)7	-1477 + 0,5147 + +2,742x IO"2 72 --1,6534х10 '6 73	[6]
5	-15000 + 7,3 7			[7]
6	(-13 390 xFe + 24 270хМп)х (1-7/1100)			[8]
7	А7 = А"	A7 = A“	-30 805 + 23,103 7	[9]

Данные различных авторов для Е“_м и Е^ и, соответственно, для Л" и А⁷ существенно различаются не только по величине, но и по знаку. Для ГЦК сплавов можно отдать предпочтение данным [5], полученным на основе экспериментов с гальванической ячейкой. Однако измерения в этом исследовании проводились при 1073-1273 К, поэтому поведение А⁷ ниже 1073 К остается неопределенным. По существу, у нас нет критерия, позволяющего выделить данные какой-либо работы как более надежные.

В ситуации, когда проведение точного эксперимента при пониженных температурах, по-видимому, затруднительно, вполне естественно обратиться к компьютерному моделированию интересующей нас величины. Цель данной работы заключается в расчете энергии смешения ОЦК и ГЦК сплавов Fe-Mn, Fe-Cr, Fe-Ni при 0 К, а также локальных магнитных моментов на атомах растворенного элемента и железа, анализ величин которых помогает понять природу концентрационной зависимости энергии смешения.

2.1 . Детали расчета

Расчет был произведен при помощи пакета TB-LMTO-ASA версии 4.7. Для моделирования различных концентраций использовалась суперячейка из 54 атомов железа для ОЦК решетки и 32 атомов для ГЦК решетки; некоторые из них случайным образом заменялись на атомы марганца. Таким образом, проводилось моделирование сплавов с содержанием марганца от 0 до 50 ат. %. В приближении локальной спиновой плотности с использованием обменнокорреляционного потенциала Барта-Хедина [13] проводились расчеты полной энергии, плотности электронных состояний и величины магнитного момента отдельных атомов для ферро- и ан-

Физика

тиферромагнитного состояний системы. Ошибка, связанная с использованием приближения атомных сфер, корректировалась введением так называемой комбинированной поправки [12, 14]. Во всех случаях использовался ЛМТО-базис, включающий s-, р- и (/-функции для каждого атома в суперячейке. При интегрировании по зоне Бриллюэна была применена сетка в к -пространстве из 8x8x8 узлов, что обеспечивало по данным проверочных тестов точность вычисления полной энергии не хуже 0,5 миллиридбергов.

Энергию смешения определяли по выражению:

^Есм = ^£tot - ^Fe - 0 -     ’                               (³ )

где E_tot - полная энергия сплава Fei^Y,; Е_¥е и Е^ - полные энергии соответствующих элементов (все в расчете на один атом). В расчетах использовались экспериментальные значения для постоянных решеток неупорядоченных сплавов, взятые из работы [15].

2.2    Результаты расчетов и их обсуждение

Результаты расчета энергии смешения при 0 К представлены на рис. 1. Отметим, прежде всего, что значения Е_см имеют отрицательный знак. Это означает, что данные сплавы склонны к упорядочению. Модуль энергии смешения возрастает при увеличении концентрации марганца до 50 %. Концентрационную зависимость £_см можно описать уравнением

5^,(0) = -15 500 хРел:Мп,Дж/моль,                         (4)

характерным для регулярных растворов. Таким образом, ^z(0) = -15 500 Дж/моль. Сравним это значение с данными табл. 1. Примерно такое же значение, но для области температур 800-1000 °C получили методом измерения ЭДС авторы [7]. Отметим также результаты измерения для 1450 К: АЯХ --(18OOO±5OOO)xMn xFe Дж/моль [2]. Можно предположить, что энергия взаимообмена в интервале 0-1450 К практически не зависит от температуры и принимает значение -15 500 ±700 Дж/моль.

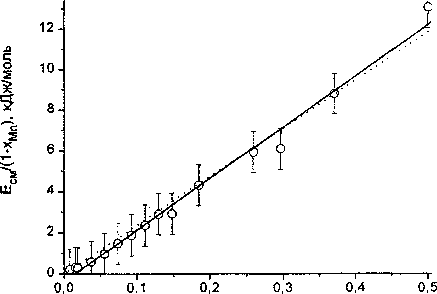
Растворы марганца в «-железе имеют иной знак энергии смешения: она положительна. На рис. 2 представлены результаты расчета в координатах Е_см /(1 - х_Мп) и х_Мп.

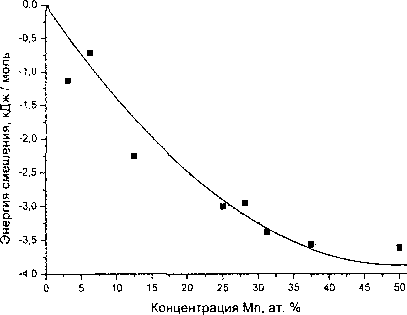
Рис. 1. Концентрационная зависимость энергии смешения у-растворов системы Fe-Mn: черные квадраты - результаты расчета, сплошная линия - аппроксиманта, описываемая уравнением (4)

хМп, содержание марганца в атомных долях

Рис. 2. Энергия смешения ОЦК твердых растворов системы Fe-Mn: кружки -результаты расчета, прямая линия -аппроксиманта в области концентраций выше 1,5 ат. %, пунктир - линейная аппроксиманта, проходящая через начало координат

Видно, что уравнение прямой

Еа

---= 25 200 (хМп - 0,015), Дж/моль

0-^Мп)

достаточно точно аппроксимирует полученную зависимость при хМп > 0,015. Все точки соответствуют случаю, когда магнитные моменты атомов железа и марганца совпадают по направлению («ферромагнитная ориентация»). При концентрации марганца 0,015 прямая должна пересечь ось абсцисс, т.е. энергия смешения - сменить свой знак, как это раньше наблюдалось для сплавов Fe-Cr [10]. Однако при хМп <0,015 оказывается более устойчивой конфигурация, когда магнитные моменты атомов примеси устанавливаются антипараллельно моментам матрицы.

Результаты наших расчетов не подтвердили подавляющее большинство данных для энергии смешения ОЦК сплавов, приведенных в литературе (см. табл. 1). В некоторых случаях отличие проявляется не только по величине, но и по знаку. Единственным исследованием, результаты которого близки к нашим, является работа Хиллерта [5], по которой А“ = 19 000 Дж/моль. Дело в том, что экспериментального изучения теплоты смешения ОЦК сплавов системы Fe-Mn не проводилось, потому что область «-растворов в данной системе очень ограничена и по концентрациям, и по температуре. Отметим результаты нашего расчета разности энергий ОЦК и ГЦК струк тур марганца:

^G⁷ - °G“)_Mn = Е^_п -^мп = -1,3 мРб/атом = -1700 Дж/моль.            (6)

Близкое к этому значение получено термодинамическим методом в работах [3] и [5]:

ДЦГ^-15 000 + 7,3 7, Дж/моль; A"G^ =-1800 + 1,276 7, Дж/моль.        (7)

Поскольку магнитная структура ферромагнитных сплавов Fe-Mn до сих пор изучены не дос таточно полно, то значительное внимание было уделено расчетам величины и ориентации магнитных моментов атомов сплава (рис. 3). При малых содержаниях Мп (менее 1,5 ат. %), реализуется строго антипараллельное упорядочение магнитных моментов марганца и железа, поскольку величина среднего момента атомов Мп совпадает с значением модуля момента. Такое поведение согласуется с более общими результатами работ Изюмова и Медведева (цит. по [26]), в которых показана принципиальная возможность переориентации примесного спина под влиянием других атомов марганца. Поскольку магнитное взаимодействие между атомами марганца, растворенными в железе, носит антиферромагнитный характер, то при строго антипараллель-ном упорядочении относительно ферромагнитной матрицы железа магнитные моменты любой пары атомов марганца будут параллельны, поэтому их магнитная энергия будет повышаться. Чтобы избежать роста магнитной энергии некоторые, вероятно, ближайшие друг к другу атомы марганца начинают менять ориентацию момента по отношению к железу с

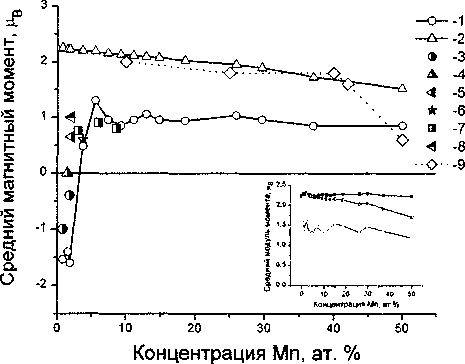
Рис. 3. Магнитные моменты в сплавах Fe-Mn: верхние кривые - средний магнитный момент на атом сплава: 2 - наш расчет, 9 - эксп. данные [21,24]; нижняя кривая - средний магнитный момент атомов Мп:

1 - наш расчет; эксп. данные 3- [19]; 4 - [16]; 5и 8-[17]; 6-[21]; 7 - [18].

На вставке приведены результаты расчета модулей магнитных моментов атомов Fe (верхняя кривая), атомов Мп (нижняя кривая) и среднего модуля моментов на атом сплава. Экспериментальные данные относятся к комнатной температуре

антипараллельной конфигурации на параллель

ную. Число таких атомов монотонно возрастает по мере роста концентрации Мп. По нашим расчетам при концентрации 2 ат. % число атомов, находящихся в параллельной и антипараллельной конфигурации, примерно сравниваются, так что наблюдается нулевое значение среднего момента у атомов марганца. При дальнейшем росте содержания Мп примерно до 6-8 ат. % проявляется все возрастающее преобладание параллельной ориентации. Однако, начиная с 8 ат. % Мп, средний момент атомов марганца стабилизируется при значении порядка 1дв, что существенно ниже наблюдаемой величины среднего модуля момента, равной примерно 1,4//д (см. вставку на рис. 3). То же самое справедливо и в отношении моментов атомов железа.

• 3.    Сплавы Fe-Cr

  3.1    Сплавы с ОЦК решеткой

Система Fe-Cr играет исключительную роль при конструировании специальных сталей. Сплавы имеют объемно-центрированную кубическую решетку и обладают ферромагнетизмом

Физика

ниже температуры Кюри (для составов с х_Сг< 0,8) или антиферромагнетизмом ниже точки Нееля (для х_Сг > 0,8).

Для моделирования различных концентраций была выбрана суперячейка из 1 б атомов железа в правильной ОЦК решетке; некоторые из них случайным образом заменялись на атомы хрома. Таким образом, проводилось моделирование сплавов с содержанием хрома от 0 до 100 ат. % с шагом 6,25 ат. % (всего 17 точек). Малые значения концентрации хрома, недостижимые в ячейке из 16 атомов (1,85 ат. % и 3,7 ат. %) были рассчитаны в ячейке из 54 атомов. Была исследована концентрационная зависимость полной энергии и энергии смешения системы. Первое исследование авторов по этой проблеме [10] позволило установить, что в области концентраций хрома 0,06 < х_Сг< 1 энергия смешения положительна, как это давно установлено термохимиками [2, 4]. Но в области небольших содержаний хрома (2-6 ат. %) энергия смешения оказалась отрицательной с минимумом вблизи 4 ат.% хрома (рис. 4). Этот результат был подтвержден исследованиями Абрикосова и Олссона [11], проведенными практически одновременно с нашей работой. Концентрация, при которой Е_см меняет знак, в этой работе оказалась равной 6 ат. %. Обнаруженный эффект является новым и имеет важные следствия для физического металловедения, поскольку означает, что твердые растворы системы Fe-Cr в области малых содержаний хрома не будут расслаиваться при охлаждении. Он нуждается в дополнительной проверке, поскольку реальная точность расчета энергии в методе ЛМТО порядка 5 мРб. В настоящей статье проводится новый и более полный анализ указанной проблемы на основе использования более точного первопринципного метода линейных присоединенных плоских волн.

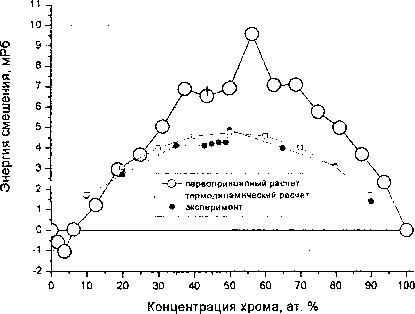
Рис. 4. Зависимость энергии смешения сплава от концентрации хрома

На рис. 5 приведено сравнение результатов расчета энергии смешения для экспериментальных значений параметра решетки и для равновесных значений, при которых достигался минимум расчетной величины полной энергии. Как видно из рисунка, равновесные значения оказались весьма близки к экспериментально наблюдаемым, что свидетельствует об адекватности используемого нами приближения для обменно-корреляционной энергии.

3 -

— Q— Экспериментальные параметры решетки

—А— Равновесные параметры решетки

0-й

0,20

Содержание хрома

Рис. 5. Зависимость энергии смешения от содержания Сг, полученная для двух типов значений параметров решетки: кружки - экспериментальные данные, треугольники - равновесные значения параметра решетки, полученные в данном расчете методом FP LAPW

Наиболее важным результатом проведенных расчетов является подтверждение смены знака энергии смешения на отрицательный в системе Fe-Cr при небольших концентрациях (до 15 %) хрома. Данный факт может быть использован для объяснения экспериментальных результатов работ [23], где наблюдалось возникновение локального ближнего порядка в сплавах железо-хром с низким содержанием хрома. При этом область концентрации при которых наблюдалось подобное упорядочение

(до 15 % Сг) хорошо согласуется с областью, где в наших расчетах получено значение Е_т1Х < 0.

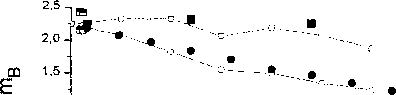
Результаты расчета концентрационной зависимости магнитных моментов атомов железа и хрома, а также среднего момента на атом сплава приведены на рис. 6 в сравнении с известными литературными данными [24, 25].

Мирзоев А.А., Ялалов М.М., Мирзаев Д.А.

Отметим, что при почти линейном убывании величины среднего момента на атом сплава, изменение локальных моментов на атомах хрома и железа обладает рядом интересных особенностей. Во-первых, в области небольших концентраций хрома (примерно до 15 ат. %) наблюдается некоторое возрастание среднего магнитного момента атомов железа, которое затем сменяется монотонным убыванием - этот факт очень хорошо согласуется с экспериментом. Во-вторых, в указанной области резко возрастает магнитный момент на самих атомах хрома.

Средний магнитный момент атомов хрома на малых концентрациях (1,85 ат. %) повторяет экспериментальную тенденцию к возрастанию, обнаруженную Кайзаром и Паретте [25]. Появление довольно значительного по величине магнитного момента на атоме хрома не является удивительным. Как уже отмечалось выше, проведенные

^   1,0-

о 1 -п-2 -А- 3 -В- 4

-Л 5 -е-6 -■-7

Л 8

• 9

.0,5-                                 ------------- ф -го- . А /

• -1,5 -

• -2,0---г-----,------,------1------,------1------,------,------,------;------,------1------,------,------,------1------,------;------,------р

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45 0,50

Содержание Сг

Рис. 6. Рассчитанные методом FP-LAPW (линии с незаполненными символами) и экспериментально измеренные (линии с закрашенными символами) магнитные моменты в системе Fe-Cr как функция содержания хрома: 1,6,9- средний магнитный момент сплава; 2, 4, 7 -средний момент на атомах Fe; 3, 5, 8 - средний магнитный момент на атомах Сг. (7, 8, 9-данные работы [24]; 4, 5, 6 - данные работы [25])

нами и имеющиеся в литературе расчеты обнаружили, что одиночная примесь хрома ориентиру ет свой магнитный момент антипараллельно моментам атомов железа, причем появление атома хрома вызывает возмущение магнитной структуры в обширной области решетки железа, окружающей атом. Вероятно, поэтому энергия магнитного (антиферромагнитного) взаимодействия железа и одиночного атома хрома оказывается высокой, и это приводит, в частности, к повышению точки Кюри. Однако появление второго атома хрома сначала в далеком, а затем все более близком окружении атома хрома приводит к нарушению антиферромагнитного упорядочения атомов Fe и Сг. Это приводит к росту энергии, поэтому атомы хрома начинают эффективно отталкиваться, что приводит к положительному знаку энергии смешения. Отметим, что вновь, как и в системе Fe-Mn, аномальное изменение энергии смешения в системе «железо-хром» обусловлено сильным возмущением магнитной структуры a-железа при очень малой концентрации при меси.

Если для ОЦК растворов существуют обширные термодинамические данные [10], которые, в общем, согласуются с результатами первопринципных расчетов для О К, то для ГЦК сплавов экспериментальные результаты практически отсутствуют, а все оценки получены косвенным методом на основе анализа y^ia равновесия в этой системе. Например, согласно расчетам Кирхнера [26]:

4еСг = 13100-31,82-Т + 2,748-7Чп7\ Дж/моль,                  (8)

откуда для О К получаем положительное значение ЭреСг — 13,1 кДж/моль, что означает склон ность данных растворов к расслоению.

Полученные данные для энергии смешения у-сплавов приведены на рис. 7. Энергия смешения оказалась отрицательной, и этот результат резко расходится даже по знаку с термодинамическими данными [26, 28]. Результаты расчета аппроксимированы на рис. 7 уравнением

Е^ = -27 500-х(1-х), Дж/моль, (9) из которого следует, что ГЦК растворы системы Fe-Cr близки к регулярным, причем обладают большой по модулю и отрицательной по знаку энергией взаимообмена Лр_е__Сг = -27,5 кДж/моль. В растворах такого типа действительно должны проявляться тенденции к упорядочению.

Второе очень значительное расхождение между принятыми для ГЦК растворов термодинамическими функциями [28, 29, 26] и результатами расчетов проявилось в оценке величины энер-

Физика____________________________

гии ГЦК-хрома °Е^ и соответственно разности °Е^_Г~°Е“_Г = &°Е^“. По данным [29,30,26], \°Е^“ =670; 1920 и 10 460 Дж/моль соответственно.

Наши расчеты показали, что при 0 К

°Е^_Х -°Е“_Х = 27,3 мРб/атом = 35 800 Дж/моль, и этот результат подтвержден аналогичными первопринципными расчетами в работах [11] и [31], где были получены соответственно значения 28,4 и 32 мРб/атом. Среднее значение по результатам трех расчетов составляет

\°Е^^а = 29,23 мРб/атом = 38530 Дж/моль .                   (10)

Знаки разности энергий, полученные в нашем расчете, а также в расчетах Кауфмана и Кирхнера, конечно совпадают, ибо хром имеет ОЦК решетку вплоть до точки плавления, однако по величине полученное нами значение отличается более чем в три раза. Интересно сопоставить энергии смешения ГЦК- и ОЦК-растворов рассматриваемой системы. Энергии взаимообмена у этих фаз, при приблизительно одинаковой по модулю величине, имеют противоположные знаки. ОЦК растворы имеют положительную энергию смешения и поэтому у них приблизительно ниже 800 К наступает расслоение однородного «-твердого раствора на две фазы, обогащенную и обедненную хромом. Напротив, в хромистом аустените должны проявиться эффекты упорядочения. Наша оценка точки Курнакова для у-сплава с 50 ат. % хрома

2-1

О

S

Э

-2-

$ -4-

■5

Fe-Cr, ГЦК

V

-6-|--------,--------1--------,---------(--------(--------1--------,---------;-------------------1--------I--------1--------,--------1--------,--------]-----------------1--------1--------,

О    10    20    30    40    50    60    70    80    90   100

Концентрация хрома, ат. %

Рис. 7. Зависимость энергии смешения ГЦК-сплавов системы Fe-Cr от содержания хрома: сплошная линия - результаты расчета, пунктир -аппроксимация зависимостью

Е^, — —21 - х(1 — х) мРб/атом

дает Т_к = А^у Ur « 600 К . Отсюда следует, что в температурно-концентрационной области существования у-фазы дальний порядок реально возникнуть не может, но эффекты ближнего порядка наблюдаться должны. Возможно, что именно этот эффект возникновения ближнего порядка типа упорядочения в аустените Fe-Cr был обнаружено в мессбауеровском эксперименте [27].

Итак, результаты первопринципных расчетов дают основание заключить, что термодинамическое описание системы Fe-Cr с ГЦК решеткой, принятое в настоящее время, по-видимому, является недостоверным и нуждается в пересмотре.

Система Fe-Ni

Сплавы Fe-Ni уже много лет используются для изучения закономерностей мартенситного у—>а-превращения [32], а также аномалий теплового расширения [33]. В работе [32], ставшей классической, Кауфман и Коэн обобщили все имевшиеся в то время термодинамические данные о системе Fe-Ni (теплоёмкости, теплоты превращения, температуры 70) и на этой основе получили уравнения температурной зависимости термодинамических параметров для этой системы:

A °G^^y = 5029 -11,0 • 10"³ 7² + 6,44 • 10'⁶ 7³;

А °G^ = -15 481 + 2,966 • 10"³ Т² +1,363 ■ 10^-6 Т³;

А^т -А^а =15 062 + 2,427 7(1-InГ), Дж/моль.                       (11)

Наши расчёты, относящиеся к 0К, дали существенно иные значения: AGye-z(0) = 5,30 мРб/атом = 6985 Дж/моль и Аб^ЦО) = -7,50 мРб/атом =-9820 Дж/моль, которые, однако, не столь сильно отличаются от значений (11) при 0 К, как для сплавов Fe-Cr.

Зависимость энергии смешения компонентов для ГЦК твёрдых растворов от концентрации никеля представлена на рис. 8. Энергия смешения изменяет свой знак вблизи л_№ = 0,5. Такое поведение Е^ в значительной мере обусловлено изменением характера магнитного взаимодейст-

Мирзоев А.А., Ялалов М.М.,          Первопринципные расчеты энергии смешения и магнитных

Мирзаев Д.А. __________________ моментов компонентов сплавов Fe-Mn, Fe-Cr и Fe-Ni...

вия от ферромагнитного (х№ > 0,25) до антиферромагнитного (xNi < 0,25), что отражает концентрационная зависимость среднего магнитного момента на атом (рис. 10).

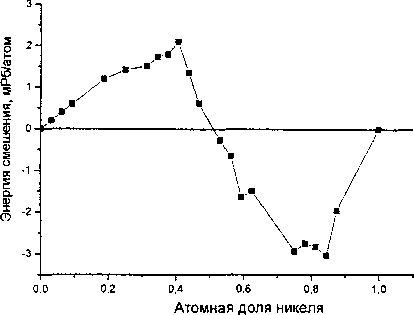
Рис. 8. Концентрационная зависимость энергии смешения ГЦК-растворов Fe-Ni

Энергии смешения для ОЦК растворов рассчитаны нами до концентрации х = 0,32 (рис. 9). Как и в случае ГЦК растворов, Е“_м имеют положительный знак, а по величине ненамного превышают Е^, . Следовательно, как у-, так и ос-сплавы Fe-Ni склонны к расслоению. Косвенным подтверждением знака Е“_м служит значительное положительное отклонение концентрационного хода параметра решётки ос-сплавов от закона Вегарда [34].

Рассчитанные значения индивидуальных магнитных моментов атомов компонентов ц и средних величин "ц в ОЦК растворе даны на рис. 10. Магнитный момент атомов железа ненамного возрастает, а атомов никеля убывает с увеличением содержания никеля. Для нестабильной ОЦК решётки никеля наши расчеты дают параметр решётки 2,805 А и магнитный момент 0,54 р._в, причём ферромагнитная ориентация более устойчива, чем антиферромагнитная.

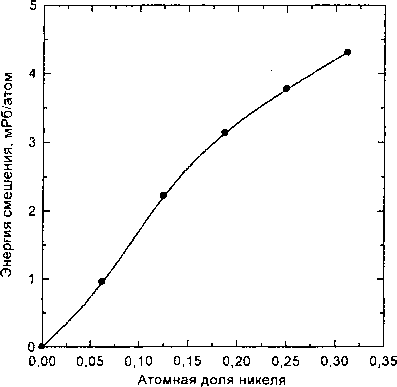
Рис. 9. Концентрационная зависимость энергии смешения ОЦК-растворов

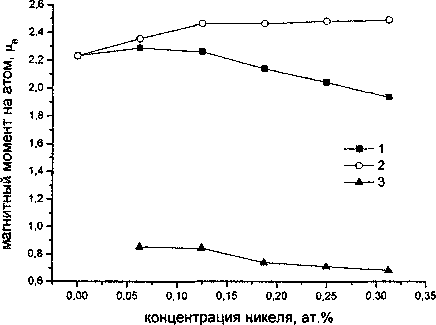
Рис. 10. Результаты расчёта атомных магнитных моментов в ОЦК сплавах системы Fe-Ni: 1 - средний момент на атом сплава; 2 - момент на атомах Fe; 3 - момент на атомах Ni

Поэтому возможно, что при концентрациях х > 0,32 снижение магнитного момента атомов никеля будет продолжаться. Средний магнитный момент на атом, пропорциональный намагниченности, обнаруживает слабый максимум вблизи х = 0,15. Экспериментальные данные по намагниченности подтверждают этот результат. Имеются данные о том, что добавки никеля снижают

Физика

точку Кюри a-железа, поэтому положительный знак энергии смешения у ОЦК сплавов обусловлен уменьшением энергии магнитного взаимодействия при возрастании концентрации никеля.

Выводы

• 1.    Проведено первопринципное моделирование энергии смешения ОЦК и ГЦК неупорядоченных бинарных сплавов системы Fe-Mn, Fe-Cr, Fe-Ni методами ЛМТО и полнопотенциальным методом присоединенных плоских волн. Показано, что расчетный метод позволяет получить достаточно точные результаты для энергии смешения (погрешность порядка ±0,5 мРб/атом), которые не в состоянии обеспечить ни один термохимический метод.

• 2.    Исследована магнитная и электронная структура указанных сплавов. Построены концентрационные зависимости магнитных моментов на атомах примесного элемента и железа, а также среднего момента сплава.

• 3.    Показано, что при 0 К твердые растворы марганца в ГЦК- и ОЦК-железе близки по поведению к регулярным растворам, но имеют разные по величине и знаку энергии взаимообмена и соответственно энергии смешения: Лр_е__Мп =-15,5 кДж/моль, Лр_е__Мп =+23,7 кДж/моль. Можно утверждать, что ГЦК растворы склонны к упорядочению, тогда как ОЦК растворы - к расслоению.

• 4.    Для a-твердых растворов Fe-Mn вблизи 1,5 % Мп имеется термодинамическая аномалия -изменение концентрационной зависимости энергии смешения, обусловленная переориентацией магнитных моментов атомов марганца.

• 5.    Показано, что энергия смешения ОЦК сплавов Fe-Cr меняет знак с отрицательного на положительный при увеличении концентрации хрома выше 10 ат. %. Эффект смены знака энергии смешения связан со спецификой обменного взаимодействия атомов железа и хрома: при малом содержании атомов хрома, последние ориентируют свой спин антиферромагнитно спинам атомов железа. Именно этой ситуации соответствует отрицательный знак энергии смешения.

• 6.    Установлено, что ГЦК сплавы Fe-Cr характеризуются при 0 К отрицательной энергией взаимообмена атомов Fe и Сг: Лр_е__Сг = -27,5 кДж/моль, а энергия смешения имеет концентрационную зависимость Е_см =-27,5 х (1-х) кДж/моль, характерную для регулярных растворов. Разность энергий ГЦК- и ОЦК-хрома при 0 К составляет согласно нашим расчетам 35,8 кДж/моль, что близко к результатам уже опубликованных исследований: 37,2 кДж/моль и 42,0 кДж/моль.

• 7.    Энергия смешения Fe и Ni в ГЦК растворах при 0 К сложным образом изменяется в зависимости от концентрации никеля х. При возрастании х энергия смешения Е^_м проходит через максимум, пересекает нулевое значение и проходит через минимум в области отрицательных значений.

• 8.    Энергия смешения ОЦК сплавов Fe-Ni, рассчитанная в интервале х = 0...0,32, положительна, что означает склонность таких сплавов к расслоению.