Петрографические структуры: ийолиты и уртиты Хибин

Войтеховский Ю. Л. и др. Петрографические структуры: ийолиты и уртиты Хибин. Вестник МГТУ. 2021. Т. 24, № 2. С. 160–167. DOI:

При изучении горной породы прежде всего уделяется внимание ее организации из минеральных фаз, обозначаемой терминами "структура" и "текстура". При более глубоком исследовании модальный (объемный или весовой минеральный) и химический составы характеризуются количественно, но описание структур и текстур остается большей частью вербальным. Структура и текстура есть у любой горной породы. Их систематика, созданная поколениями геологов, использует индукцию, т. е. обобщение всевозможных характеристик составных частей горной породы: метрических (абсолютные и относительные размеры: афанитовая, мелко-, средне- и крупнозернистая, равно- и неравномернозернистая, порфировидная и порфировая структуры) и неметрических (панидио-, гипидио- и ксеноморфнозернистая структуры) характеристик минеральных зерен, их форм (призматически-зернистая и спинифекс-структура), особенностей пространственных отношений минеральных зерен (пойкилитовая структура) и агрегатов (такситовая и полосчатая текстуры), а также непосредственных (т. е. видимых в микроскоп) генетических представлений (лепидогранобластовая структура). Таким образом структуру и текстуру трактуют учебники ( Марин, 2015 ), словари ( Левинсон-Лессинг и др., 1963; Петрографический словарь, 1981 ) и различные нормативные документы ¹ ( Петрографический кодекс…, 2008 ).

Авторами настоящего исследования развиваются математические подходы – дедуктивный и моделирование, использующие естественное представление о кристаллической горной породе как системе минеральных зерен разных видов, контактирующих по два (в объеме – по поверхностям, в шлифе – по линиям), три (в объеме – по линиям, в шлифе – в точках) и четыре зерна (в объеме – в точках, вероятность попадания в шлиф равна нулю). Особенность подходов – смещение акцента с элементов системы на их отношения – вероятности (рассчитанные в шлифах как частоты) различных бинарных и тернарных межзерновых контактов. Дедуктивный подход позволяет строго, в несложных математических терминах (алгебра матриц, теория квадратичных форм) определить категории петрографических структур, построить их исчерпывающую классификацию и согласованную номенклатуру, ввести в обиход структурные барицентрические диаграммы нового типа. Моделирование дает возможность заполнить барицентрические диаграммы идеальными трендами структур и текстур, так как определены типы минеральных агрегатов и их насыщение в пространстве (матрице) горной породы. Сравнение стандартного и предлагаемых подходов выполнено на образцах ийолитов и уртитов Хибинского массива, Кольский полуостров.

Материалы и методы

Индукция

На месторождении Коашва (Восточный рудник ОАО "Апатит", Хибины) из керна скв. 2843 на глубинах от 2,5 до 100 м взяты образцы горных пород ряда ийолит-уртит. Породообразующие минералы – нефелин (55–85 %, подсчитано планиметрическим методом в шлифах) и эгирин-авгит (30–10 %), второстепенный – титанит (до 10 %), акцессорные – апатит, К-Na полевой шпат, астрофиллит, лампрофиллит, рудные (1–2 %), вторичные по нефелину – канкринит и цеолиты. Текстура массивная, структура гипидиоморфнозернистая, реже панидиоморфнозернистая с элементами пойкилитовой (рис. 1). В принципиальных чертах стандартное описание этим исчерпывается.

Рис. 1. Петрографический шлиф уртита и его прорисовка (желтый – титанит; серый – нефелин; зеленый – эгирин-авгит; коричневый – биотит; фиолетовый – апатит) Fig. 1. Petrographic section of urtite and its outline (yellow – titanite, gray – nepheline, green – aegirine-augite, brown – biotite, purple – apatite)

Дедукция

Система бинарных контактов в n -минеральной горной породе представлена как n -арный автоморфизм множества { m i } 1n минералов, слагающих горную породу:

£ Р у М М = { м } ^ ^—— { m } ^ .

• I,    J = 1

Сумма вероятностей pij всех типов межзерновых контактов mi mj (= 1) показана в форме p12 ...  p1n p22 ... p2n

... ... ...

p n 2 ^... p nn

m ₁

m ₂

...

m _n

pii n                                    p21

Л P j m i m j = [ m l m 2 - m n ]

• i ,    j = 1                                                       ...

. P n l

Откуда следует важная роль симметрической матрицы Р ij , выражающей организацию (но еще не структуру) горной породы ( Войтеховский, 1995 ). В простейшем случае биминеральной горной породы вероятности { p 11 , p ₁₂ , p ₂₂ } бинарных контактов можно показать в барицентрическом треугольнике, вероятности { p 111 , p ₁₁₂ , p ₁₂₂ , p ₂₂₂ } тернарных контактов - в барицентрическом тетраэдре (рис. 2). Это новые типы структурных диаграмм в петрографии.

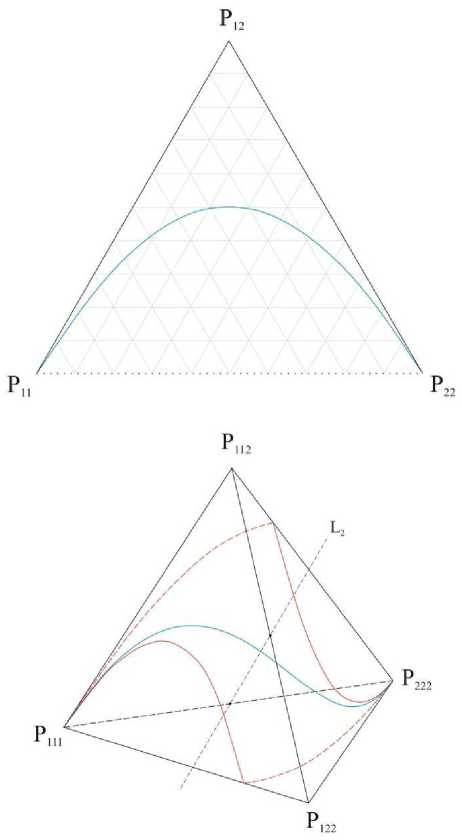
Рис. 2. Линии Х-В (голубые) в барицентрических треугольнике ( а ) и тетраэдре ( б ), следы К -поверхности на гранях тетраэдра (красные линии)

Fig. 2. H-W lines (blue) in the barycentric triangle ( а ) and the tetrahedron ( б ), K-surface traces on the tetrahedron facets (red)

В ходе дальнейшего анализа важно обсудить массивную текстуру горных пород, которая только кажется очевидной. "Массивная текстура, Науман – текстура пород зернистой структуры без особой ориентировки составных частей, однородных во всех направлениях. См. беспорядочнозернистая структура. <…> Беспорядочнозернистая структура, Розенбуш – структура без определенной ориентировки зерен, т. е. одинаковая во всех направлениях; типичная структура пород массивной текстуры" ( Левинсон-Лессинг и др., 1963, с. 42, 189 ). В данных определениях применительно к массивной текстуре (и, вероятно, только к ней) категории текстуры и структуры отождествляются, ибо здесь составные части сводятся к минеральным зернам. Но особенность массивной текстуры заключается не только в этом. Среди петрографических структур и текстур лишь она определяется математически строго как равновесие Харди – Вайнберга (далее Х-В) вероятностей p ij разных межзерновых контактов при заданных вероятностях p i минеральных зерен разных видов в n -минеральной горной породе:

• ( P i m i + + p_n m n ) 2 = £ P j m, m j ,

где p _ii = p _i ² , p _ij = 2 p _i p _j . Равновесие Х-В устанавливает идеальное перемешивание минеральных зерен в пространстве горной породы.

Поясним применение в петрографии математического аппарата, разработанного генетиками для анализа смешений родительских генов в потомстве. Смысл его заключается вовсе не в наследовании признаков, будь то живые организмы или горные породы одного семейства, происходящие из одной исходной магмы, или конвергентные им горные породы, образовавшиеся в сходных условиях. Авторов интересует именно формальный математический аппарат, найденный независимо Г. Х. Харди (Англия) и В. Вайнбергом (Германия): если даны взаимодействующие агенты в парциальных долях p _i и p j , то приведенные выше формулы позволяют рассчитать их идеальное перемешивание, т. е. баланс различных взаимодействий. Отклонение от такового в генетике рассматривается как "дрифт". Именно таким образом рассчитываются равновесия химических реакций, смешений родительских генов в потомстве, баланс хищников и жертв в биологических популяциях, а также вероятности различных межзерновых контактов в данной статье.

Для биминеральных горных пород линия равновесия Х-В задается соотношением р 11 р ₂₂ = ( р_Х2 / 2 ) 2 в барицентрическом треугольнике (рис. 2). Неожиданность состоит в том, что массивные текстуры образуют не поле диаграммы, а границу, на которую фигуративная точка реальной текстуры (для которой подсчитаны Р 11 , Ри , P 12 ) попасть не может. Это кажется странным, ведь массивные текстуры известны во всех классах горных пород. Но, как показано, отнесение текстуры к массивной – статистическая задача, каждый раз решаемая с помощью критериев согласия. Авторами рассчитана линия равновесия Х-В и в барицентрическом тетраэдре (рис. 2). Ради простоты изложения принципиальных моментов далее используются вероятности бинарных контактов и барицентрический треугольник.

Линия равновесия Х-В – важная классификационная граница в барицентрическом треугольнике: для всех точек ниже ее p 11 p ₂₂ >  ( p ₁₂ /2 ) 2 , выше - p 11 p ₂₂ <  ( p ₁₂ /2 ) 2 . Для каждой точки диаграммы квадратичная форма ∑ p _ij m _i m _j определяет одну из структурных индикатрис – центральных линий 2-го порядка: ниже линии Х-В – эллипс, выше – гиперболу, на линии – пару параллельных прямых. Соответствующая классификационная граница ( К -поверхность) построена и в барицентрическом тетраэдре (рис. 2). Тип индикатрисы устойчив в пределах поля диаграммы, меняется лишь ее геометрия (от точки к точке эллипс и гипербола поворачиваются в системе координат { т 1 , m 2 }, изменяются их эксцентриситеты). В общем случае петрографическую структуру можно определить как инвариантный аспект организации горной породы, алгебраически выражаемую канонической диагональной формой симметрической матрицы P _ij и геометрически визуализуемую структурными индикатрисами – поверхностями 2-го порядка ( Войтеховский, 2000 ). Согласованная номенклатура возможных петрографических структур для n -минеральной горной породы проста: символ S _n ^m означает, что в канонической диагональной форме матрицы Р _ij ровно m положительных чисел.

Моделирование

В статье (Войтеховский и др., 2020) моделирование предложено в качестве нового метода изучения структур и текстур горных пород. Всякая модель специализирована в отношении некоторых характеристик объекта. Авторами использованы вероятности бинарных контактов в биминеральных горных породах. Показано, что при фиксированных кластерах и их насыщении в матрице классические структуры (вкрапленные, порфировидные, порфировые, с ветвящимися кластерами, цепочечные, пойкилитовые) и текстуры (шлировые, полосчатые) образуют тренды, закономерно заполняющие барицентрический треугольник (рис. 3). В горных породах формы кластеров строго не определены. Тем не менее фигуративные точки их структур и текстур должны закономерно располагаться между некоторыми идеальными трендами.

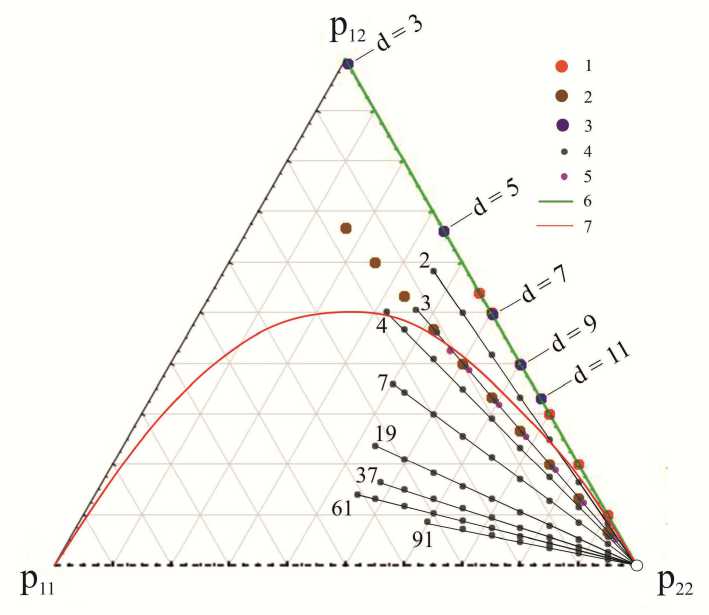
Рис. 3. Барицентрическая диаграмма вероятностей ( p ii , p jj , p ij ). Модельные структуры и текстуры: 1 – вкрапленная; 2 – цепочечная; 3 – порфировые ( d – диаметр фенокриста); 4 – шлировые (количества зерен в шлирах указаны числами); 5 – с ветвящимися кластерами;

6 – пойкилитовые; 7 – линия равновесия Харди – Вайнберга

Fig. 3. Barycentric diagram of ( p _ii , p jj , p _ij ) probabilities. Model structures and textures: 1 – disseminated, 2 – chained, 3 – porphyric ( d – the diameter of phenocryst), 4 – schlieren (quantities of grains in the schlierens are indicated by numbers), 5 – with brunching clusters, 6 – poikilitic; 7 – the Hardy – Weinberg equilibrium line

Результаты и обсуждение

Для девяти образцов горных пород Хибинского массива в петрографических шлифах найдены числа различных бинарных межзерновых контактов. Так, для одного из них (образец 1 на рис. 4):

559 157,5 4 24,5 157,5 6 1,5 5 4 1,5 0 1 24,5 5 1 4 где первые строка и столбец соответствуют нефелину, вторые – эгирин-авгиту, третьи – акцессорным минералам в целом, четвертые – титаниту; порядок строк и столбцов не важен, но важно, чтобы матрица была симметрической. Приведением к диагональному виду (Боревич, 1988; Гантмахер, 1988) установлено, что образцы 1, 6-9 имеют структуру S42, образцы 2-5 - структуру S43. Для их визуализации нужны многомерные барицентрические диаграммы. Поэтому далее девять исходных матриц сведены к "биминеральным" последовательным противопоставлением нефелина, эгирина и титанита матрице, т. е. всем остальным минералам в целом. Так, объединением строк и столбцов из данной матрицы получаем три матрицы:

559 186 1   Г 6 164 1 Г 4 30,5

186 25 ’ 164 622 ’ 3 0,5 891

Приводя их к диагональному виду (для матриц 2 х 2 - посредством подсчета определителей), получим, что две первые отвечают структуре S21, третья - S^, т. е. положение титанита в матрице образца 1 радикально отличается от положения нефелина и эгирин-авгита. Наоборот, установлено, что в образце 6 структурная роль всех трех минералов та же ( S21 ). Результаты показаны в барицентрических треугольниках на рис. 4. Их анализ в сравнении с идеальными трендами (рис. 3) обнаруживает важные особенности.

• (1)    На всех диаграммах фигуративные точки образуют компактные поля: на рис. 4 (справа) – поле, тяготеющее к линии равновесия Х-В (массивная текстура) при очень редких срастаниях титанита; на рис. 4 (в центре) – совпадающее с трендом пойкилитовых структур; на рис. 4 (слева) – поле между ними, покрывая тренд шлировых текстур с небольшим числом минеральных зерен в агрегатах. Эти особенности организации видны на рис. 1. По сравнению со стандартным описанием барицентрические диаграммы позволяют охарактеризовать их количественно.

• (2)    По соотношению эгирин-авгита и матрицы (рис. 4, в центре) все девять образцов уверенно относятся к структурному типу S ₂ ¹ (индикатриса – гипербола). На двух других диаграммах некоторые точки попадают в поле структур S ₂ ² (индикатриса – эллипс), например, точки 2 и 3 (рис. 4, слева). Но 2 – это уртит, 3 – ийолит, т. е. разные породные типы, выделенные по содержаниям нефелина и эгирин-авгита, могут иметь одинаковые структуры. И наоборот, в одном породном типе возможны разные структуры: ийолиты 1 и 3, уртиты 2 и 4 (рис. 4, слева). Но заметим, что принятый в минералогии конституционный принцип требует отнесения природных кристаллических фаз с разными структурами к разным минеральным видам. Применяя тот же принцип к горным породам, мы должны отнести ийолит 3 и ийолиты 1, 9 к разным породным типам. Это важно в связи с тем, что границы между ийолитами и уртитами по содержанию нефелина строго не определены. Соотношения модального состава и структуры горной породы (при строгом определении категории структуры) напоминают изоморфизм и полиморфизм в кристаллохимии.

• (3)    Предыдущее замечание указывает на важность положения фигуративной точки структуры относительно линии равновесия Х-В (и других классификационных границ, которые появляются в барицентрическом тетраэдре и многомерных симплексах при рассмотрении n -минеральных структур и статистик тернарных межзерновых контактов). Так, нет абсолютной уверенности в положении фигуративных точек в поле структуры S ₂ ² (рис. 4, слева и справа). Для принципиального решения вопроса следовало бы увеличить статистику P _ij , изучив больше шлифов для соответствующих образцов. (На математическом языке – совершить предельный переход от эмпирических частот к вероятностям.)

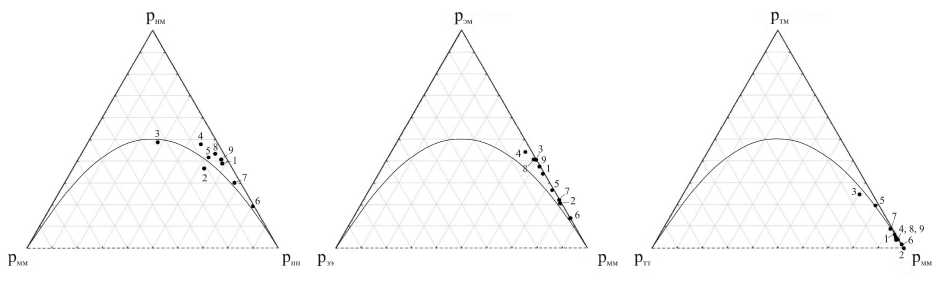
Рис. 4. Фигуративные точки структур ийолитов и уртитов Хибинского массива в барицентрическом треугольнике вероятностей бинарных контактов: н – нефелин; т – титанит; э – эгирин; м – матрица; образцы 1, 3, 9 – ийолиты; образцы 2, 4–8 – уртиты Fig. 4. Figurative points of the structures of ijolites and urtites of the Khibiny massif in the barycentric triangle of probabilities of binary contacts. Letters indicate: н – nepheline, т – titanite, э – aegirine, м – matrix; samples 1, 3, 9 – ijolites, samples 2, 4–8 – urtites

Заключение

Развиваемый авторами анализ петрографических структур и текстур на основе статистик бинарных и тернарных межзерновых контактов имеет термодинамическую основу. Межзерновые границы в горных породах (а также металлах и сплавах) рассматриваются многими авторами как граничные дефекты кристаллических структур, зоны обрыва химических связей и каналы свободной энергии ( Салтыков, 1958; Жабин, 1979; Беленький, 1980; Вернон, 1980; Бродская, 1988 ). После установления в горной породе физикохимического равновесия наступает период дополнительной минимизации их свободной энергии. При описании межзерновых границ целесообразно учесть их протяженность, в физическом приближении – удельные свободные энергии. В этом видится перспектива развития метода.

Три подхода к описанию петрографических структур и текстур (индуктивный, дедуктивный, моделирование) дополняют друг друга. Стандартный подход идейно исчерпан, два других – на стадии разработки. Надо признать, что получаемые количественные характеристики еще предстоит по мере возможности приспособить для генетических реконструкций. Исторический пример – кристаллохимия, постепенно наполняющая физическими интерпретациями изначально геометрические (впрочем, столь же алгебраические) кристаллографические модели (решетки, правильные системы точек, точечные и пространственные группы симметрии и т. д.).

Авторы благодарят рецензента за конструктивные замечания, способствовавшие более точному изложению результатов исследования.