Пьезопреобразователи для возбуждения упругих волн терагерцевого диапазона в графеноподобных 2D-супракристаллах

Анализ состояния разработок ведущих зарубежных исследовательских учреждений в области СВЧ-электроники [1] показывает, что так называемая «терагерцевая щель» (THz Gap) от 0.3 ТГц до 3.0 ТГц, отделяющая электронику от фотоники, в настоящее время начинает интенсивно осваиваться. Уже созданы малогабаритные вакуумные электронно-лучевые приборы (клистроны и лампы бегущей волны), работающие на частотах от 220 ГГц до 1030 ГГц. Широкая полоса частот терагерцевого излучения, спо-

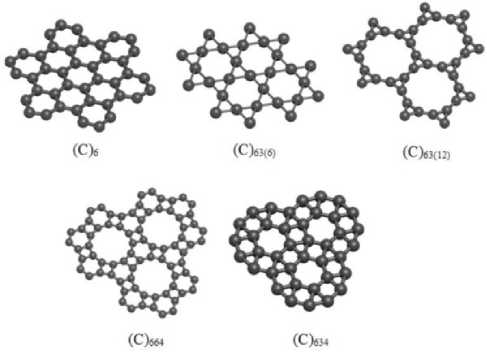
Рис. 1. Атомные модели исследуемых графеноподобных наноразмерных структур: графен (С)6 и углеродные 2D-супракристаллы. Первый индекс обозначает вид супра- ячейки (гексагональная), последующие – вид ячеек вложения. Индексы в скобках определяют вид многоугольника в центре ячейки в случае одинаковых ячеек вложения собность проникать через непрозрачные среды (дым, туман, пыль, одежду, упаковку и т. п.) определяют перспективы его применения в высокоскоростных линиях связи, радиолокационных системах высокого разрешения, антитер-рористических системах обнаружения оружия, взрывных устройств и т. д. Кроме того, переход на терагерцевые частоты позволит поднять быстродействие микропроцессорной техники на несколько порядков.

Вместе с тем для практического освоения те-рагерцевого диапазона, помимо создания компактных источников терагерцевого излучения, необходимо разработать соответствующие элементы волноводного тракта и устройства обработки сигналов. В сочетании с терагерцевой электроникой и плазмоникой весьма перспективным представляется также развитие тера-герцевой наноакустоэлектроники. В работах [5–6] нами рассчитаны упругие характеристики и скорости распространения продольных, поперечных и изгибных упругих волн в графене и графеноподобных 2D-супракристаллах. Высказаны перспективы использования таких волн в устройствах двумерной, в т. ч. терагерцевой, акустоэлектроники и акустооптики. В этой связи обнадеживающим фактором является экспериментальное обнаружение акустических колебаний терагерцевого диапазона частот в нанораз-мерных структурах [7].

Важнейшим элементом любого акустоэлек-тронного устройства является электроакустический преобразователь, предназначенный для преобразования электромагнитного сигнала в упругую волну той же частоты и наоборот. В СВЧ-диапазоне наибольшее распространение получили пьезоэлектрические преобразователи. Принципы их конструирования и расчета были разработаны еще в конце 60-х – начале 70-х гг. прошлого века [8–12], однако особенности возбуждения упругих волн терагерцевого диапазона в графеноподобных 2D-структурах требует отдельного рассмотрения. Этому и посвящена настоящая работа.

1. Исследуемые материалы и их пьезоэлектрические характеристики

На рис. 1 представлены атомные модели графена (С)6 и предложенных нами [5; 13] графеноподобных 2D-супракристаллов. Их отличительной особенностью является то, что в узлах шестиугольников находятся не отдельные атомы, а их симметричные комплексы. Некоторые из них, например (С)63(12) и (С)664, как и графен, характеризуются sp2-гибридизацией орбиталей валентных электронов и являются полуметаллами. Другие – (С)63(6) и (С)634 – sp3-гибридизацией и отличной от нуля шириной запрещенной зоны.

Все приведенные 2D-кристаллы принадлежат к классу точечной симметрии 6/mmm, т. е. обладают центром симметрии и не являются пьезоэлектриками. В работе [14] предлагается решить эту проблему путем создания в графене отверстий треугольной формы. При этом симметрия кристалла понижается до нецентросимметричного класса 3m, характеризуемого наличием полярной оси симметрии. При взаимном смещении подрешеток кристалла вдоль этого направления в результате механических деформаций возникает электрическая поляризация (пьезоэффект).

Уравнение пьезоэффекта для полученных таким образом двумерных пьезоэлектриков может быть записано в виде д u

P i = e ijk ( i , j , k = 1,2 ) . (1) д X k

Здесь Pi – вектор электрической поляризации, определяемый как дипольный момент, приходящийся на единицу площади, величина которого измеряется в системе СИ в кулонах на метр (Кл/м); eijk – тензор пьезоэлектрических коэффициентов, также измеряемых в Кл/м; дUj / дXk — тензор деформаций, выраженный через производные от смещений по координа- там.

Элементарные ячейки исследуемых перфорированных двумерных кристаллических структур в сравнении с ячейкой графена показаны на рис. 2. Для получения максимального дипольного момента на единицу площади плотность «оборванных» электронных связей должна быть как можно больше, поэтому треугольные «атомные дырки» сделаны минимальными по размеру и расположены периодически. Их рекомендуется создавать при помощи пучка электронов высокой энергии [14].

Матрицы упругих жесткостей ( c_ij ) и пьезоконстант ( e_ij ) для этих структур могут быть легко получены путем редукции соответствующих матриц для трехмерных кристаллов [15; 16] и имеют вид

^ ^c 11 ^c 12          0

^c 12 ^c 11          0

0    0 2 ^{( c} 11 - ^c 12 ) ,

0     0    - ^e 22

.- ^e 22 ^e 22     0

Здесь использованы матричные представления тензоров c_ijkl и e_ijk путем свертки по парам симметричных индексов: 11 ^ 1; 22 ^ 2; 12, 21 ^ 3.

Из матрицы пьезоконстант видно, что в перфорированных вышеуказанным образом графеноподобных 2D-супракристаллах электриче- ское поле, приложенное вдоль направления x1, вызывает деформацию сдвига в плоскости (x1, x2). Если же электрическое поле приложено в направлении x2, то возникает деформация растяжения вдоль оси x1 и сжатия вдоль оси x2, а при смене полярности поля – наоборот.

Единственный независимый компонент вектора поляризации в (1) может быть найден согласно его определению как p = Zea u ,                            (2)

• ² S д x₂

где Z – число «оборванных» электронных связей в элементарной ячейке; e – элементарный заряд; a – длина ребра супраячейки; S – пло- щадь элементарной ячейки. Выражения для этих параметров приведены в табл. 1. Используя их и приравнивая правые части выражений (1) и (2), получаем для пьезоэлектрического коэффициента e22 следующую формулу:

e e22 = Fl ’

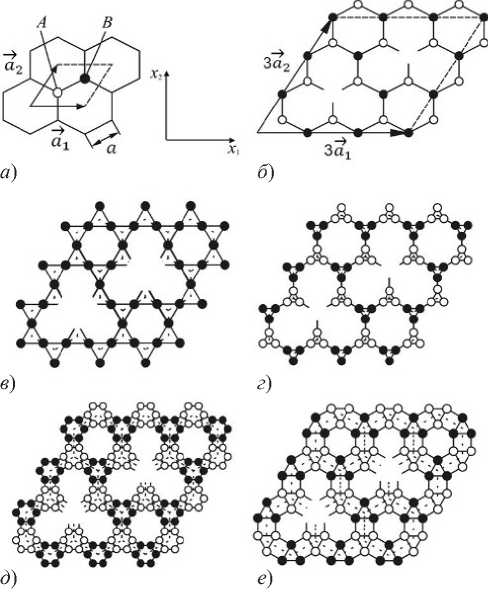
Рис. 2. Элементарные ячейки графена ( а ), перфорированного графена ( б ) и углеродных 2D-супракристаллов (С)₆₃₍₆₎ ( в ), (С)₆₃₍₁₂₎ ( г ), (С)₆₆₄ ( д ), (С)₆₃₄ ( е ). Атомы, образующие подрешетки типов А и B , показаны соответственно в виде светлых и темных кругов

где F – форм-фактор, определяемый параметрами структуры (см. табл. 1.), а l – длина межатомной связи. Вычисленные по формуле (3) значения пьезоконстанты e ₂₂ для перфорированного графена и графеноподобных 2D-супракристаллов также представлены в табл. 1. При этом значения l брались из работы [17].

Значение 622 = 2.83 ■ 10 10 Кл / м для графена характеризует двумерный пьезоэффект. Поделив эту величину на эффективную толщину графенового листа, обычно принимаемую за расстояние между слоями в графите 3,35 А, получаем для эквивалентной пьезоконстанты, описывающей трехмерный пьезоэффект, значе-(3)                        2

ние e22 = 0.84 Кл / м . Для сравнения: в цитируемой работе [14] получено значение e22) = 0.124 Кл/м2. Однако оно получено для единичного отверстия в графеновой наноленте. В случае регулярных отверстий оптимального размера, естественно, должен наблюдаться более сильный пьезоэффект.

Обратим также внимание на то, что значения 3 e ₂₂ для углеродных 2D-супракристаллов с sp -гибридизацией примерно вдвое меньше, чем в графене и sp³-наноаллотропах. Это связано, как видно из табл. 1, с меньшими значениями их

о w                             х

Рис. 3. Анализируемая модель пьезоэлектрического преоб- разователя, находящегося в акустическом контакте со зву-копроводом: 1 – пьезопреобразователь (перфорированный графен); 2 – звукопровод (графен)

форм-фактора, т. е. фактически с большей рыхлостью структуры.

• 2.    Вносимый импеданс пьезопреобразователя

На рис. 3 изображена анализируемая модель пьезоэлектрического преобразователя (ПП) (1), нагруженного на звукопровод (2). И сам ПП, и звукопровод выполнены из одной графеновой наноленты, ориентированной вдоль кристаллофизической оси x ₂. Та часть конструкции, которая является ПП, перфорирована периодически расположенными треугольными отверстиями, причем основания треугольников также ориентированы вдоль оси x ₂. Как отмечалось выше, периодическое электрическое поле, приложенное к ПП в направлении x ₂, будет возбуждать колебания растяжения-сжатия, которые будут распространяться вдоль звукопровода в виде продольных упругих волн. Такая стыковка ПП со звукопро-водом обеспечивает наилучший акустический контакт между ними, что очень важно на тера-герцевых частотах.

Состояние пьезоэлектрика при выбранной ориентации ПП описывается следующими уравнениями:

д U 2

t 22 = ^c 2222 7      ^e 222 E 2 ,                            ⁽⁴⁾

^{д x}2

D 2 = 6 222 u + S 22 E 2 ,                        (5)

^{д x} 2

где t 22 , C 2222 , 6 222 , ^ 22 — соответствующие компоненты тензоров упругих напряжений, упругих жесткостей, пьезоэлектрических констант и диэлектрических проницаемостей; u ₂ – механическое смещение; E ₂ и D ₂ – соответственно компоненты векторов напряженности и индукции электрического поля. Обозначив ось x ₂ как x и опустив индексы, перепишем систему (4)–(5) в более простом виде:

t = c — - eE ,                                (6)

д x

D = e ^ u -_e E .                               (7)

д x

Подробные практические рекомендации по расчету параметров ПП для возбуждения СВЧ-акустических волн в кристаллах изложены в работе [18]. Здесь мы будем следовать предложенной в ней методике, принимая во внимание двумерный характер задачи. В частности, величины, входящие в формулы (6), (7), измеряются в следующих единицах СИ: [ t ] = 1 Н / м, [ с ] = 1 Н / м, [ д и / д x ] = 1, [ e ] = 1 Кл / м, [ E ] = 1 В / м, [ D ] = 1 Кл / м, [ б ] = 1 Ф.

Импеданс, вносимый ПП в электрическую цепь, в квазистатическом приближении можно найти как ww

E ( x , t ) dx      E ( x , t ) dx

Z (_Ю) = U = Ao---------- = Jo---------- ,     (8)

^{v 7} I      b д D / д t         i to bD ( t )

где U и I – соответственно мгновенные значения приложенного к ПП напряжения и силы про- текающего в нем тока; w и b – двумерная «тол- щина» и ширина ПП.

Выражая E из (7) и подставляя результаты в

(8), получаем

Z ( to )

Здесь

w

—

i toБ b

w

w 1

-----= —б ----= — iX ( to ) i toБ b        to C o

– емкостное сопротивление ПП, определяемое его статической двумерной емкостью C o = б b / w . Действительная часть второго слагаемого показывает активное сопротивление излучения ПП, которое мы обозначим R ( to ), а мнимая — малую добавку к реактивному емкостному сопротивлению, обусловленную пьезоэффектом.

Смещение частиц упругой волны в пьезослое можно представить в виде и ( x, t) =

= иo+exp [-i (kx — tot)] + иo—exp [i (kx + tot)], где иo+ и иo— — комплексные амплитуды, определяемые граничными условиями, а k – волно- вое число:

to k = — = w v1

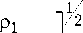
с ( 1 + K ² )

В выражении (11) v ₁ – скорость упругой волны в пп; Р 1 — его двумерная плотность; K – коэффициент электромеханической связи в материале ПП:

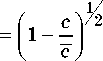
определяемый величиной пьезоэлектрического «ужесточения» его модулей упругости продольной компонентой электрического поля [5; 6; 18–20]:

e ²

с = с +--.(13)

б

Граничные условия задачи выглядят следующим образом:

t1 (x = o) = o(14)

– напряжение на свободной границе ПП равно нулю;

t1 (x = W) = t2 (x = w)

– напряжения на границе раздела ПП и звуко-провода одинаковы.

Подставляя (7) в (8), а результат в (14), (15), можно получить два линейных алгебраических уравнения для и o ₊ и и o _— . Тогда (9) удается привести к виду

Z ( to ) = R ( to ) — iX ( to ) ,                              (16)

Удобно ввести R ( to ) to C o = 5 ( kw ) — безразмерное активное сопротивление излучения, описываемое уравнением

5 ( kw ) =

4 K ²             sin⁴ ( kw /2 )               (17)

^kw ( Z o1 / Z o2 ) sin^{2 kw +} ( Z o2 / Z o1 ) ^cos 2 ^kw

Здесь опущена упомянутая выше малая добавка к реактивному емкостному сопротивлению, обусловленная пьезоэффектом. Входящие в (17) величины Z o1 = Р 1 V 1 и Z o2 = Р 2 V 2 представляют собой характеристические акустические импе-дансы ПП и звукопровода соответственно.

На рис. 4 представлены универсальные для всех ПП рассматриваемого типа зависимости 5 ( kw ) / K ² от постоянной распространения kw для различных значений отношения Z ₀₁ / Z ₀₂: 1–1.2; 2–1.1; 3–1.0; 4–0.9; 5–0.8. Приведенные кривые позволяют для заданной частоты сигнала to _o выбрать оптимальные значения двумерной толщины ПП w_opt . Затем, зная ширину ПП b , легко найти его емкостное сопротивление на данной частоте X ( to o ) = w opt / б bw и сопротивление излучения R ( to o ) = 5 ( k o w opt ) X ( to o ) .

• 3.    Численные оценки

0.2 дБ / см ■ ГГц [22], или, в пересчете на терагерцы, 20 дБ / мкм ■ ТГц².

• 4.    Коэффициент электроакустического преобразователя

Произведем численные оценки параметров ПП на основе графена, для которого известны значения упругой жесткости С 22 = С ц = 533 Н/м [2], относительной диэлектрической про- ( r )      ( r )      ( r )

ницаемости б22' = бЦ = Б|| ' = 1.8 [21] и с исполь-

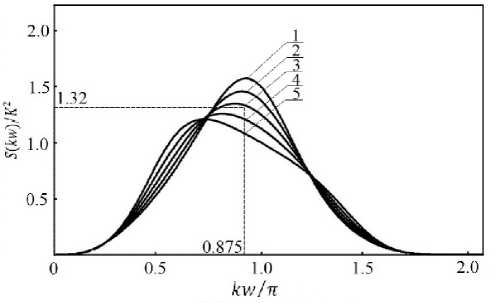
Рис. 4. Зависимость безразмерного сопротивления излучения пьезопреобразователя от постоянной распространения акустической волны для различных значений Z ₀₁ / Z ₀₂: 1–1.2; 2–1.1; 3–1.0; 4–0.9; 5–0.8

хания может быть сделана на основе того факта, что затухание продольных звуковых волн в Z-срезе сапфира ( a -A^O g ) — типичного материала для СВЧ-акустоэлектроники – составляет 2

Отсюда ясно, что длина звукопровода вряд ли может быть больше нескольких микрометров. Тогда ширина ПП, скорее всего, должна составлять доли микрометра. Примем ее равной 10 w opt = 0.124 мкм. В этом случае емкостное сопротивление ПП будет X ( m q ) = 2.98 МОм, а сопротивление излучения R ( m q ) = 0.26 МОм. Для сравнения: типичные значения этих сопротивлений на гигагерцевых частотах составляют десятые и сотые доли ома соответственно [18]. Причина здесь в том, что для возбуждения объемных упругих волн в кристаллах на гигагерцевых частотах используются ПП, в которых электрическое поле прикладывается перпендикулярно к пленочному пьезоэлементу толщиной в доли микрометра. В результате емкость такого ПП велика, а емкостное сопротивление мало. В нашем случае электрическое поле прикладывается вдоль ПП, площадь эффективного сечения которого исключительно мала. По этой причине емкость ПП мала, а емкостное сопротивление и, как следствие, сопротивление излучения очень велики по сравнению с волновым сопротивлением стандартной линии передачи.

Под коэффициентом электромеханического преобразования ПП понимают отношение мощности возбуждаемой им акустической волны к мощности подаваемой на него прямой электромагнитной волны:

Р„

П = p a .                                      (18)

Поскольку вся выделяемая в нагрузке, каковой является ПП, СВЧ-мощность

P = ( 1 -|Г|² ) P + ,                                      (19)

где |г| — модуль коэффициента отражения в передающей линии, расходуется на мощность P_a возбуждаемой акустической волны и мощность потерь P_s в ПП:

P = P a + P_s ,                                    (20)

то из (18)–(20) следует, что

^П ( 1 I ^Г ) R (^) + r_s ( to ) ^. (²¹⁾ При выводе формулы (21) учтено, что P a х R ( to ) , а P s х R s ( to ) , где R s ( to ) — сопротивление потерь в ПП, обусловленное главным образом конечной величиной электропроводности ПП.

При комнатной температуре подвижность носителей заряда в графене ц = 25 м² / ( В ■ с ) [23]. В его элементарной ячейке, площадь которой приведена в табл. 1, находится 2 свободных электрона, таким образом, их поверхностная концентрация составляет n = 4.32 ■ 10¹⁷ м ^{- 2}. Тогда коэффициент двумерной электропроводности графена ст = en ц = 1.73 Ом ^{- 1}.

Поскольку толщина графеновой наноленты заведомо меньше глубины скин-слоя, то для b = 10wopt, Rs (to) = Rs = wopt / (стb) = 0.058 Ом. Следовательно, Rs (to) ^ R (to) и, согласно формуле (21), коэффициент преобразования предложенного ПП практически полностью опреде- ляется степенью согласованности его импеданса с линией передачи. Так как

IГ f =

Z ( to ) - Z g

Z ( to ) + Z g

( R ( to ) - Z _g ) 2 + X ² ( to )

( R ( to ) + Z _g ) 2 + X ² ( to ) ,

где Z ₀ – волновое сопротивление линии передачи, то из (21), (22) ясно, что наименьшие потери энергии на преобразование электромагнитного сигнала в акустический будут при Z g = R ( to ) . В акустоэлектронных устройствах гигагерцевого диапазона, где R ( to ) значительно меньше волнового сопротивления стандартной передающей линии, для понижения величины Z ₀ обычно применяют трансформаторы сопротивления [18]. В нашем случае, когда R ( to ) » Z g , по-видимому, придется отказаться от идеи использования даже повышающих трансформаторов. Разумной альтернативой здесь представляется прямое «оптическое» возбуждение ПП сигналом терагерцевой частоты с выхода генератора.

Заключение

Из вышеизложенного следует, что возбуждение упругих волн терагерцевого диапазона в графеноподобных наноразмерных материалах вполне реализуемо, хотя и на пределе возможностей современных нанотехнологий. При этом наибольшие трудности вызывает даже не изготовление электроакустических пьезопреобразователей, а их согласование как электрической нагрузки с генератором терагерцевого излучения.

Следует отметить, что недавно был предложен еще один способ превращения графена в пьезоэлектрик – его допирование электроположительными или/и электроотрицательными атомами [24]. В этом случае деформации растяжения-сжатия вдоль наноленты создаются поперечным к ней электрическим полем. Это позволяет резко уменьшить импеданс электроакустического ПП и, казалось бы, облегчить проблему его согласования с передающей линией. Однако использование микрополосковых линий передачи в данном случае затруднено в связи с большими потерями на излучение и затухание на терагерцевых частотах. Плазмонные волноводы ввиду отсутствия в них поперечных электрических полей здесь не могут быть использованы. Как вариант могут быть предложены волноводы на электрогидродинамических волнах свободных носителей заряда, физическая природа и свойства которых описаны нами в работах [25–28].

В целом авторы выражают уверенность в том, что акустические волны терагерцевого диапазона в графеноподобных 2D-супракристаллах в скором времени найдут применение в высокоинформативных быстродействующих линиях задержки, фильтрах, корреляторах и других привычных для СВЧ-акустоэлектроники устройствах обработки сигналов. Более того, использование их взаимодействия со сфокусированным лазерным излучением позволит разработать широкий круг терагерцевых аналогов классических аку-стооптических устройств: модуляторов, дефлекторов, сканеров, анализаторов спектра и т. п.

Работа выполнена при финансовой поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009–2013 гг. (Соглашения №№ 14.В37.21.1083, 14.В37.21.1285, 14.В37.21.1653) Российского фонда фундаментальных исследований (проект № 12-02-31054) и Министерства образования и науки Российской Федерации (Государственное задание № 2014/232).

Таблица 1

Расчетные параметры и пьезоэлектрические константы перфорированных графеноподобных углеродных 2D-супракристаллов

Параметры	(С) 6	(С) 63(6)	(С) 63(12)	(С) 664	(С) 634
Z	6	12	6	12	12
a	l	23 l 3	( 2 + Va) Va 3 l	( a + Va ) Va 3 l	( 1 + Va) Va 3 l
S	27 3 l 2 2	18 3 l 2	9Va ( 2 + Va ) 2 2 2 l	9Va ( a + Va ) 2 2 2 l	9 ( 1+^ ) 2 l 2 2
F	43 27	4 9	4 9 ( 2 + Va )	8 9 ( a + Va )	8 9 ( 1 + Va)
l , А	1.42	1.86	1.71	1.56	2.17
e 22 , 10 - 10 Кл/м	2.83	3.69	1.12	1.89	2.39

Таблица 2

Механические и акустические параметры пьезопреобразователя и звукопровода

Параметры	p , 10 7 кг / м2	c , Н/м	v , 103 м/с	Z 0 , 10 2 кг / ( м ■ с )
пьезопреобразователь	6.77	548	28.5	1.93
звукопровод	7.60	533	26.5	2.01