PID Controller Parameters Tuning Based-on Satisfaction for Superheated Steam Temperature of Power Station Boiler

Published Online June 2014 in MECS

With the development of science and technology and the deepen understanding to the natural science and the process nature, it was found that the traditional optimization theory and optimization techniques have also been difficult in solving many problems. So people begin to introduce the research results in the other fields of science and technology into the field of optimization theory and algorithm, it mainly includes two types, one is to improve the existing optimization algorithms and introduce the new calculation theory, another is to extend or adjust the optimization theory itself, namely, use satisfaction to replace optimization, early the satisfaction criterion was proposed, later the concepts of satisfaction and satisfaction solution were proposed.

The satisfaction criterion is a kind of innovative thinking, it will break the people’s thinking mode in the solving problem, and it will take people from the study of pure rational thinking to a limited rational state, and provide a new way for people to solve the problem. Satisfactory optimization is a product of satisfaction principle and optimization theory, its core idea is in optimization problems, it don't put emphasis on getting the optimal solution, but according to the specific situation to seek satisfactory solution of the problem. The biggest characteristic of satisfactory optimization method is in the solving process, it will abandon the traditional concept of "optimal", and put emphasis on "satisfactory", it will consider uniformly the satisfactory design of system performance index and the optimization of system parameters, also consider uniformly the constraint condition of optimization problems and the object function, so this satisfactory optimization method has the extensive applicability and flexibility, and has been applied in many aspects[1,2,3,4].

Random number direct search method (LJ method) uses random number direct iterative search, after each iterations it can reduce the search range with rules, and find the optimal value until to expect accuracy. LJ method is simple, at the same time it can be convenient to the addition of various constraints conditions, so the application range of this method is extensive. The biggest deficiency of LJ method in practical application is that the number of cycle calculation is large and the consumption of machine time is long, and convergences to the optimal with the slow speed. References [5][6] improved LJ method, that is modified NLJ method, it is better than the original LJ method in the convergence rate, and has been used in the system model identification, the controller and filter design.

This paper is to study the combination of satisfaction thought and the direct search method of random number, and apply this method to PID control parameters tuning for Power Station Boiler Superheated Steam Temperature.

The remainder of this paper is organized as follows: In Section 2, Firstly, aiming at the shortcomings of selecting the evaluation function of a single performance index in many PID parameters tuning, the paper proposes a new comprehensive satisfaction function as the integrated evaluation function of performance index. Secondly, aiming at the parametric uncertainty in superheated steam temperature such as rise time t , regulation time t , overshoot Г % and steady state error ess, in this paper, the fuzzy constraint is introduced to the comprehensive satisfaction function design. Also the steps of PID parameter optimization by using NLJ algorithm and fuzzy constraint idea are presented. In Section 3, aiming at the superheated steam temperature control system of Power Station Boiler, the superheated steam temperature object model is presented, simulation verification and experimental verification are done. Conclusion is given in the final section.

• II.    PID Parameters Tuning based-on NLJ Algorithm and Satisfaction Idea

• 2.1    Comprehensive Satisfaction Function

In recent years, w ith the development of adaptive control, predictive control, fuzzy control, neural network etc. artificial intelligence technology, many intelligent PID parameter tuning method are presented based-on the adaptive and self-tuning technology, but the generality is limited. While the tuning method of PID parameters is based on various optimization, there are still some difficulties in the determining of object function and the selection of optimization strategy[7-17].

The idea of comprehensive satisfaction function is: in the solution of optimization problem of large system, firstly simplify the complex problem into simple links, secondly synthesize the simple links together to solve complex problems. According to this idea, the design method can be obtained for the comprehensive satisfaction function, the detailed design idea is:

Set up a problem with n solution x. ( i = 1,2,- nr ), J_k ( k = 1,2,- m ) is each performance index of the system in the solution X = { x _t, x ₂,- - x _n} , it is not realistic for each J to achieve the optimal in the production process, define s _k as the satisfaction function value of J , the comprehensive satisfaction function can be written as follows:

k = m

^S = f ^{( S} 1 , ^S 2 ," " s m ) = 5 w k s k               ⁽¹⁾

k = 1

m

The weights ^ w_k = 1 in (1), S is the linear weight k = 1

of each satisfaction, it is a comprehensive evaluation of all performance indexes, weight settings will reflect the attention degree of the decision-maker to the corresponding performance index. If decision-maker thinks that a change of a satisfaction greatly influences the whole comprehensive satisfaction, the larger weight will be selected, otherwise, a smaller weight is select, and the weight has normalized form, apparently S e [0,1], the control objective of satisfactory is to make S close to 1. But the comprehensive satisfaction evaluation has a shortage, when satisfactory solutions are more and a few satisfaction solutions is very small, now comprehensive satisfaction in practice is not satisfied, but the comprehensive satisfaction obtained from the use of (1) is satisfactory. So formula (1) is modified as follows:

k=m_ i

S = f(s1$ s 2,"-sm) = ( ^ wkSk )(П si )

k=1

l

Where: ^^ S i is the product of satisfactory solutions i = 1

that their thresholds are less than 6 , that is S_t <  0 ( i = 1,2,* -7 ), its significance is: when the satisfaction of certain solution is too small, we think that the overall satisfaction is very poor, at this time the comprehensive satisfaction will be leaded to the sharp decline, threshold is the bottom line that decision makers can tolerate certain solutions, and it will be determined according to the need of practical production requirement.

• 2.2    Comprehensive Satisfaction Function Design with Fuzzy Constraint

The main indexes for the measure of a PID control system performance are: rise time t , regulation time t , overshoot Г % and steady state error ess. Aiming at the superheated steam temperature the design requirements of performance index are as follows: the rise time is not more than 300s, regulation time is not more than 1000s, the maximum overshoot is less than 5%. According to the different requirements of each performance index, the satisfaction functions with fuzzy constraint attributes[18] are designed as follows:

Rise time:

, = 11, tr<300

1   | exp(-20(tr-300)2), tr>300

Regulation time:

s 2

/1, t s < 1000

' exp( - 20( t_s - 1000)²), t s > 1000

Overshoot:

s 3

1, г<5% exp(-50(г-0.05)2), г>5%

In order to eliminate the system static error, select the steady-state error e as a performance index, define its satisfaction function:

s4 = eXp (-80< )                         (6)

In conclusion, define the comprehensive satisfaction function:

5 = 0.2 s + 0.2 s2 + 0.3 s3 + 0.3 s4             (7)

Take threshold в =0.5, when a certain satisfaction is less than 0.5, at this time the comprehensive satisfaction function is modified as follows:

l

5 = (0.2 s + 0.2 s2 + 0.3 s3 + 0.3 s4 )^ st      (8)

i = 1

• 2.3    PID Parameter Optimization Steps based-on NLJ Algorithm

The steps of PID parameter optimization by using NLJ algorithm are as follows:

Step1: Select 2000 random numbers between (-0.5， 0.5), divide these numbers into 100 groups, the matrix representation is y     , its elements are represented as yki, k = 1,2,-100, i = 1,2,-20.

Step2: Let hypothesis, estimated PID parameters are a ( i ) , i = 1,2,3 , each element in a ( i ) represents the PID control parameters k , k , k respectively, set the initial value a ⁽ 0 ) ( i ) , while the search range r ⁽¹⁾( i ) is several times larger than the initial value. That is:

r(1)(i)=Con a(0) (i) (9)

Where: the digital in brackets represents the number of iterations, 1 represents the first iteration, 0 represents the initial value, Con represents the constant, 2 may be selected.

Step3: Determine the performance index. Adopt the comprehensive satisfaction function formula (7) or (8) as the performance evaluation function for the optimization of PID parameter tuning.

Step4: Do the iterative computation of parameters optimization. First, 3 random numbers are selected from the first group of random number, mark y _{1 z}, i = 1,2,3 . The parameter values will be calculated as following formula:

a(1) (i) = a(0 (i) + yu*r (1) (i) (10)

For a control system, the stability of the system is the most important condition. Therefore, combine the PID parameters a ^{( 1 )} ( i ) by formula (10) calculation with the model of control object, and obtain the new model of closed-loop system, and then judge whether they meet the condition of the system stability. If meet, then calculate the comprehensive satisfaction S according to the performance index evaluation function. If the stability condition is not satisfied, abandon the set of parameters and do search again, until the searched parameters satisfy the stability conditions, also calculate S , then select y ₂Д i = 1,2,3 ) from the second groups of random numbers and repeat the calculation of (10) until the P group, select from the P group performance index that satisfies the constraints, while S is a group of the largest parameters used as the initial value of second iterations. The iterative process of the steps can be written in the general formula (11):

ak(j)(i ) = ak(j-1)( i) + yti*r(j)(i) (11)

Where: k = 1,2<- P , P = 50~100 , the group number. j = 1,2,-- * L , L = 100 ~ 200 , the number of iterations.

Step5: Select the contraction coefficient ф . The search scope r ^ ( i ) is reduced ф times after each iteration:

r(j) (i) = ф r(j 1) (i)

ф may be selected constant (such as ф =0.981), also can change ф to variable coefficient in accordance with the empirical formula, with the increase in the number of iterations, ф is accelerated reduction to improve the convergence speed.

Step6: Repeat Step4 and Step5 for the next iteration, until 100 iterations, or until a condition is satisfied (For example, after the certain iteration the satisfaction S is close to 1 and is unchangeable obviously). Generally, the NLJ method can ensure enough convergence speed, don't actually need 100 iterations, more satisfactory results can be obtained.

• III.    Superheated Steam Temperature Control of Power Station Boiler

• 3.1    Superheated Steam Temperature Object Model

The main steam temperature control of power station boiler is one of the important parameters of the unit safety and economic operation. Common control methods include the double loop control system of conventional cascade PID controller or differential compensation signal, but because of the characteristics of steam temperature controlled object with large delay and large inertia, these control methods are difficult to obtain the optimal control effect. The actual situation shows that, although many power plants have used DCS, but the control quality of steam temperature is still not ideal, steam temperature will deviate from the set value above 8 °C even when the load changes with only 2%MCR/min rate for some power plants, so often the main steam temperature can only be controlled by manual operation, also the stable range is expanded to the scope of ± 6C, this will reduce the economic operation of the unit and increase the labor intensity of operator.

The paper will use the superheated steam temperature system in an Anhui power plant #2 boiler (600MW subcritical boiler) as an example, this main steam temperature control system adopts cascade control scheme. Its inner loop adopts the P controller, the outer loop adopts PID controller, its structure is as shown in Fig. 1. In Fig. 1, у_n and /_z2 are temperature transmitter slope coefficients respectively, t1 is the steam temperature of desuperheater outlet, t2 is the steam temperature of superheater outlet. The regulating object of steam temperature includes the water spray control valve, desuperheater and superheater. The opening degree of the water spray control valve is the input signal of regulating channel, superheater outlet steam temperature t2 is the output signal.

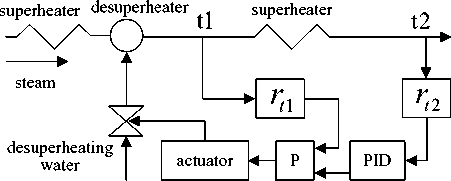
Fig. 1. Structure diagram of cascade control system for superheated steam temperature

The dynamic characteristics of the steam temperature object are composed of two parts:

• (1)    Taking the opening degree of water spray valve as the input signal and desuperheater outlet temperature t1 as the object of the output signal, this part of regulating channel is called leading section.

• (2)    Taking the desuperheater outlet temperature t1 as the input signal and superheater outlet temperature t2 as the output signal channel, this part of regulating channel is called inertial section.

0.270

The superheated steam temperature cascade control system with water spray desuperheating is shown in Fig. 2.

Fig. 2. Schematic diagram of cascade PID control system for superheated steam temperature

The identification model of boiler superheated steam temperature under 550MW load is given in reference [19,20], and choose A side primary desuperheater (leading section), forward screen and backward screen (inertial section) model as an example. The transfer function of primary desuperheater is:

(1 + 26.19 S ) e

The transfer function of forward screen A is:

_________0.482

(1 + 27.74 S )(1 + 28.65 S ) e

The transfer function of backward screen A is:

0.576

(1 + 155.59 S ) e

Inner PID algorithm parameter Kp is 50, thus comprehensive main loop model is:

_______________________3.75

(1 + 26.19 S )(1 + 27.74 S )(1 + 28.65 S )(1 + 155.59 S ) e

The paper will use this superheated steam temperature model as the controlled object, in order to maintain the inner loop invariance of original cascade system, only PID self tuning is used to the main regulator.

• 3.2    Simulation Verification

• 2.3 section, the simulation experiment is done for the above superheated steam temperature object model. The unit step response curve is shown in Fig. 3, and the optimization process curve of objective function is shown in Fig. 4. In Fig. 4, the abscissa is the iteration times, the ordinate is the satisfaction.

• 3.3    Experimental Verification

According to the satisfaction function formula (3), (4), (5),  (6) with fuzzy constraints and comprehensive satisfaction function formula (7) determined in the paper 2.2 section, and according to the PID parameter optimization steps based-on NLJ algorithm in the paper

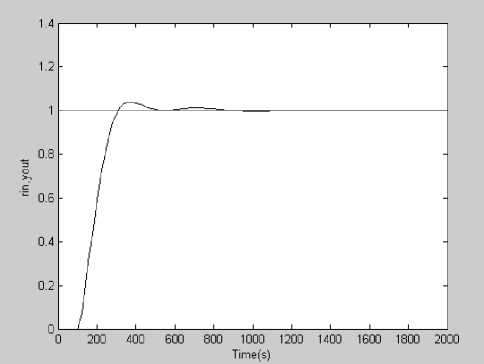
Fig. 3. The unit step response curve with PID parameters self-tuning

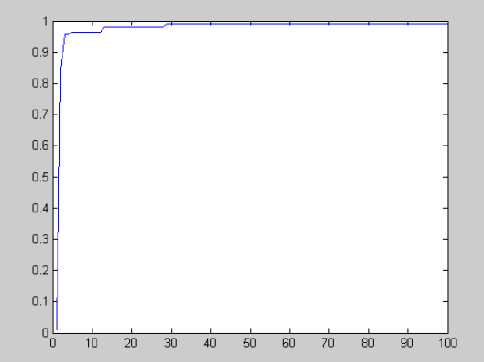
Fig. 4. Comprehensive satisfaction function curve

Seen from the curve in Fig. 3, under the satisfaction function with constraints, each performance index is no more than the constraint range, and the whole performance index is better, while the comprehensive satisfaction can meet the requirements after 20 iterations, a good search speed has been shown.

Aiming at Boiler field experiment, Research Group cooperates with Anhui Electric Power Research Institute, the dynamic characteristic experiment and control software is developed for Thermal power plant boiler, this software has real-time data acquisition, model identification, algorithm simulation and control function.

Under the unit stable operation conditions (480MW), the control experiment was done with The PID parameter tuning algorithm, the overshoot satisfaction function is modified to:

s 3

1, 7 <1% exp( 50(7-0.01)2), 7>1%

The remaining parameters remain unchanged, the main consideration is to meet the practical requirements of superheated steam temperature dynamic changes. At the same time the down load disturbance on the system was done in the steady state process, the opening degree of the valve for water spray desuperheating was became large, the experimental results show that the system output temperature come back to the set temperature 540 °C up and down after 5 C error, this result can satisfy the thermal electric power demand for ±8 C performance index, also the output temperature steady error can satisfy the thermal electric power demand for ±4C performance index.

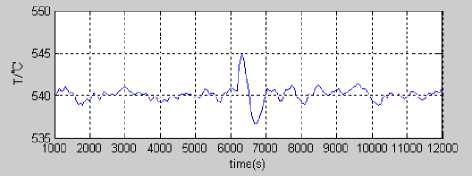
Fig. 5. Steady state and dynamic response of the main steam temperature

From Fig. 5, the controller has strong effect to inhibit overshoot, it can control the output in the constraint range very well, at the same time it has good control performance, and meets the superheated steam temperature control requirements of power plant boiler. In addition, the self-tuning PID algorithm has good robustness for the changes of the model order and parameters, and can adapt to the control of superheated steam temperature.

• IV.    Conclusion

With the development of the large capacity, high parameter and high efficiency for power plant boiler, the production system becomes more and more complex, the coupling, time-varying, nonlinear characteristics of the system become more outstanding. Among them, superheated steam temperature of high temperature superheater is a typical object of nonlinear, time-varying, large delay, large inertia. Nowadays, despite the emergence of many new intelligent control method for the control of main steam temperature, but, because the PID control structure and algorithm are simple, easy to implement, and strong applicability, it is still the most widely used control strategy. The paper proposed the PID controller parameters tuning method based-on NLJ algorithm and satisfaction idea, combined with the Anhui power plant 600MW boiler superheated steam temperature model, simulation and experimental research are done, finally the effectiveness of the algorithm is verified.

Satisfaction for Superheated Steam Temperature of Power Station Boiler