Placement and Sizing of DG Using PSO&HBMO Algorithms in Radial Distribution Networks
Автор: M.Afzalan, M. A.Taghikhani
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 10 vol.4, 2012 года.
Бесплатный доступ
Optimal placement and sizing of DG in distribution network is an optimization problem with continuous and discrete variables. Many researchers have used evolutionary methods for finding the opti-mal DG placement and sizing. This paper proposes a hybrid algorithm PSO&HBMO for optimal placement and sizing of distributed generation (DG) in radial distribution system to minimize the total power loss and improve the voltage profile. The proposed method is tested on a standard 13 bus radial distribution system and simulation results carried out using MATLAB software. The simulation results indicate that PSO&HBMO method can obtain better results than the simple heuristic search method and PSO algorithm. The method has a potential to be a tool for identifying the best location and rating of a DG to be installed for improving voltage profile and line losses reduction in an electrical power system. Moreover, current reduction is obtained in distribution system.
Distributed Generation, Distribution Networks, Particle Swarm Optimization (PSO), Sensi-tivity Analysis, Honey Bee Mating Optimization (HBMO), Voltage Profile
Короткий адрес: https://sciup.org/15010317
IDR: 15010317
Текст научной статьи Placement and Sizing of DG Using PSO&HBMO Algorithms in Radial Distribution Networks
Published Online September 2012 in MECS
One of the most important motivation for the studies on integration of distributed resources to the grid is the exploitation of the renewable resources such as; hydro, wind, solar, geothermal, biomass and ocean energy, which are naturally scattered around the country and also smaller in size. Accordingly, these resources can only be tapped through integration to the distribution system by means of distributed generation. Distributed generation (DG), which generally consists of various types of renewable resources, can be defined as electric power generation within distribution networks or on the customer side of the system [1].DG affects the flow of power and voltage conditions on the system equipment. These impacts may manifest themselves either positively or negatively depending on the distribution system operating conditions and the DG characteristics.
Positive impacts are generally called ‘system support benefits’, and include voltage support and improved power quality; loss reduction; transmission and distribution capacity release; improved utility system reliability. On account of achieving above benefits, the DG must be reliable of the proper size and at the proper locations [2], [3]. Distributed Generation is a small generator spotted throughout a power system network, providing the electricity locally to load customers. DG can be an alternative for industrial, commercial and residential applications. DG makes use of the latest modern technology which is efficient, reliable, and simple enough so that it can compete with traditional large generators in some areas [4], [5]. In fact, one type of DG is capable of supplying real power and reactive power.
A stochastic dynamic multi-objective model for integration of DG in distribution networks is proposed in [6] with a binary PSO algorithm. A distribution system expansion planning strategy encompassing renewable DG systems with schedulable and intermittent power generation patterns is presented in [7] that a solution algorithm integrating TRIBE PSO and ordinal optimization (OO) is developed to obtain optimal and near-optimal solutions for system planners. A DG interconnection planning study framework is brought in [8] that includes a coordinated feeder reconfiguration and voltage control to calculate the maximum allowable DG capacity at a given node in the distribution network. In [9] a distributed micro-grid planning model has been presented to optimize the locating and the unit capacities within DG micro-grid, in which wind power and photovoltaic power are taken into consideration simultaneously with both Elitism Genetic Algorithm (EGA) and PSO.
A multi-objective index-based approach for optimally determining the size and location of multi-distributed generation (multi-DG) units in distribution systems with different load models based on PSO is introduced in [10,11] and a combined genetic algorithm (GA)/(PSO) is presented in [12] for optimal location and sizing of DG on distribution systems. A population-based heuristic approach for optimal loca tion and capacity of DGs in distribution networks, with the objectives of minimization of fuel cost, power loss reduction, and voltage profile improvement is proposed in [13] that the approach employs an improved group search optimizer (iGSO) by incorporating PSO into group search optimizer (GSO) for optimal setting of DGs. A new hybrid method which employs discrete PSO and optimal power flow is introduced in [14] which could apply to connect distributed generation systems in a distribution network choosing among a large number of potential combinations.
-
II. Load Flow
On account of the some inherent features of distribution systems such as; radial structure, unbalanced distributed loads, large number of nodes, a wide range of R/X ratios; the conventional techniques developed for transmission systems generally fail on the determination of optimum size and location of distributed generations. The backward/forward sweep load flow algorithm is used in this paper. The voltage for all buses firstly is considered with zero phases then knowing power of bus we can find current of each bus. We use the obtained new voltages to calculate the current of buses so as the permitted repeat time is reached. After finding the line currents we use the first voltage bus to calculate the voltage of the buses. The problem is to determine allocation and size of the DGs which minimizes the distribution power losses and improve the voltage profile for a fixed number of DGs and specific total capacity of the DGs. Therefore, the following assumptions are employed in this formulation:
Objective function is defined as cost over profit. Costs include charge of active and reactive power production and the advantage is obtained from reduction of losses and variance of voltage.
sub = kpg *( p + p ) + kq*( q + q )/
DG loss DG loss
((kps * ( ploss old
-
- p ) + kq * ( q
loss loss old
+ kv * (v - — v )) v cast old v cos t
- q. ) loss
kpg is the real power production price. kq is the reP active power price. LOSS is the active power loss in P presence of distributed generator. DG is the active production power of distributed generator. qDG is the reactive production power of distributed generator. qLOSS is the reactive power loss in presence of distribP uted generator. lossold is the active power loss before installation of distributed generator. qlossold is the reactive power before installation of distributed generator. cost old is the voltage variation from ideal condition before installation of distributed generator. The price of DG power is considered to be 313 ryal/kw. Direct effect of reactive power on voltage profile kv factor can be held equal to kq. kps factor is the price of real power which is referred to 354ryal/kw.
sub = 313*( p + p ) + 82400*( q + q )/
DG loss DG loss
((354*(336 - p ) + 82400 *(264 - q ) loss loss
+ 82400 *(.45 -v )) v cast
The constraints are listed as follows:
-
a) Distribution line absolute power limits:
I PijLine l < Pij,maxLine
I PijLine l and Pij, maxLine are the absolute and its corresponding maximum allowable
power value
flowing over the distribution line between the nodes i and j, respectively.
-
b) Bus voltage limit:
Bus voltage amplitudes are limited as
Vmin < Vi < Vmax (4)
Where Vmin and Vmax are the minimum and maximum values of bus voltage amplitudes, respectively.
-
c) Power limits of DG:
PDGimin < PDGi < PDGimax,
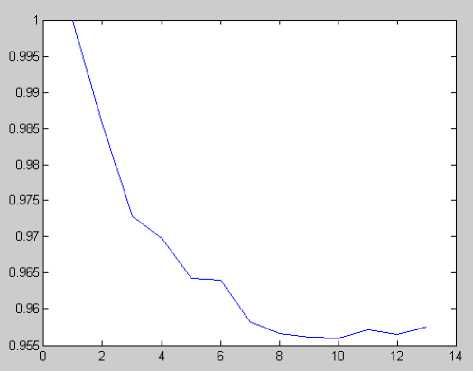
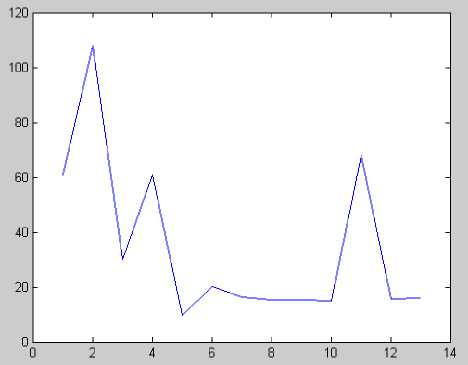
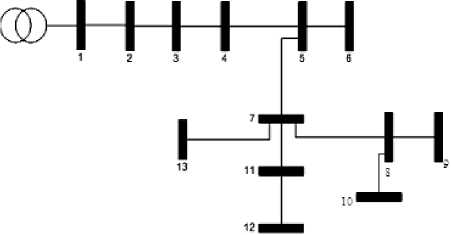
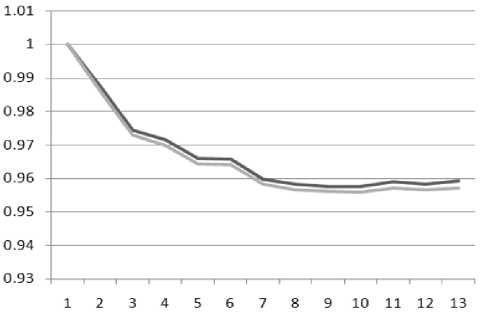
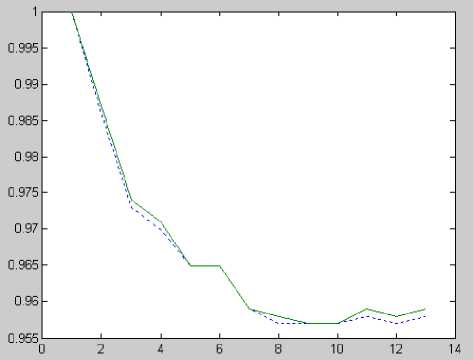
QDGimin Where Pi and Qi are the injected active and reactive power of DG components at the ith bus. d) Subject to power balance constraints: Nsc EPg .= Up z+ PL DGi DiL i=1 i=1 Where Nsc is total number of sections, PL is the real power loss in the system, PDGi is the real power generation at bus i, PDi is the power demand at bus i. In this analysis, the amounts of active and reactive power are separately increased and in each increase the magnitude of objective function will be calculated. The bus which has most variation to minimize the objective function is determined as the suitable place to install the first DG. This method is used in [15]. The amount of DG will be calculated in the next step using proposed optimization algorithm. Fig.1 shows that the best buses for DG installation are 2,11,4 respectively. Fig.1 Sensitivity of objective function to the location of DG its neighbourhoods. Generally, the value of each component in v can be clamped to the range [-vmax , vmax] to control excessive roaming of particles outside the search space. Then the particle flies toward a new position. This process is repeated until a user-defined stopping criterion is reached. A linearly decreasing inertia weight from maximum value wmax to minimum value wmin is used to update the inertia weight: w k w max — w max — w min к max • k Kmax is maximum iteration number [16, 17]. IV. HBMO Algorithm III. Particle Swarm Optimization PSO is a population-based, stochastic optimization algorithm based on the idea of a swarm moving over a given landscape. The algorithm adaptively updates the velocities and members positions of the swarm by learning from the good experiences. In PSO, the velocity vid and position xid of the dth dimension of the ith particle are updated as follows: vd = w • vd + c 1 • r1 • (pbestd - xd) + C2 • r • (gbestd - xd ) xd = xd + vd Where xi : the position of the ith particle vi : the velocity of particle i The honey bee is a social insect that can only survive as a member of a community, or colony. The colony inhabits an enclosed cavity. The honey bee community structurally consists of three different forms: the queen (reproductive female), the drone (male), and the worker (non reproductive female). These castes are associated with different functions in the colony; each caste possesses its own special instincts geared to the needs of the colony. The behaviour of honey-bees shows many features like cooperation and communication, so honey-bees have aroused great interests in modeling intelligent behaviour these years. Marriage in honey-bees optimization (MBO) is a kind of swarm-intelligence method. Such swarm intelligence has some successful applications. Ant colony is an example and the search algorithm is inspired by its behaviour. Mating behaviour of honey-bees is also considered as a typical swarm-based optimization approach. The behaviour of honey-bees is related to the product of their genetic potentiality, ecological and physiological environments, the social conditions of the colony, and various prior and ongoing interactions among these three [18, 19]. The HBMO algorithm combines number of different procedures. A drone mates with a queen probabilistically using an annealing function as follows [18, 20]: -A( f ) prob(Q, D) = e s(t) pbesti : the best location in the search space ever visited by particle i gbest : the best location discovered so far w : the inertia weight that controls the impact of previous velocity of particle on its current one r1, r2 : independently uniformly distributed random variables with range (0, 1) c1,c2 : positive constants(acceleration) coefficients which control the maximum step size Equation (7) is used to calculate the new velocity according to its previous velocity and to the distance of its current position from both its own best historical position and the best position of the entire population or where Prob(D) is the probability of adding the sperm of drone D to the spermatheca of the queen, A is the absolute difference between the fitness of D and the fitness of the queen and S(t) is the speed of the queen at time t. The probability of mating is high when the queen is with the high speed level, or when the fitness of the drone is as good as the queen’s. After each transition in space, the queen’s speed decreases according to the following equations: s(t +1) = a • s(t) 0<a<1 Where is the amount of speed and energy reduction after each transition and each step. Initially, the speed of the queen is generated at random. A number of mating flights are realized. At the start of a mating flight drones are generated randomly and the queen selects a drone using the probabilistic rule in Eq. (10). If the mating is successful (i.e. the drone passes the probabilistic decision rule), the drone’s sperm is stored in the queen’s spermatheca. By using the crossover of the drone’s and the queen’s genotypes, a new brood (trial solution) is generated, which can be improved later by employing workers to conduct local search. One of the major differences of the HBMO algorithm from the classic evolutionary algorithms is that since the queen stores a number of different drone’s sperm in her spermatheca, she can use parts of the genotype of different drones to create a new solution which gives the possibility to have fittest broods more. In real life, the role of the workers is restricted to brood care and for this reason the workers are not separate members of the population and they are used as local search procedures in order to improve the broods produced by the mating flight of the queen. Each of the workers has different capabilities and the choice of two different workers may produce different solutions. This is realized with the use of a number of single local search heuristics N worker1and combinations of them N worker2Thus, the sum of these two numbers N worker Nworker1 N workee2 gives the number of workers. Each of the broods is randomly chosen to be feed by worker, which is also randomly selected. If the new brood is better than the current queen, it takes the place of the queen. If the brood fails to replace the queen, then in the next mating flight of the queen this brood will be one of the drones. Honey Bee Mating Optimization (HBMO) algorithm can be described briefly in 5 steps as below: Step 1: This algorithm starts with flying in which the queen (the best answer) randomly selects its male pairs to consequently reproduce new bees. Step 2: the new born bees (possible answers) will be reproduced by displacing in queen and male genes. child = parent1 + β⋅ ( parent2 - parent1) 0≤β≤1 (12) Step 3: worker bees (research functions) are used to do the position seeking (breeding and improving new bee's generation). Brood. = Brood. + (5 + s) • Brood-0<ε<1; 0≤δ≤1 Step 4: Fitting functions of the workers will be sorted based on the amount of bees' generation improvement. Step 5: the best new born bee in this process can be nominated to take queen position and do the next flying process. In this article a new optimization method is presented based on the mixture of PSO and HBMO methods. Players and motion speed is calculated through PSO relations in this method and choosing or suitability is obtained from HBMO method. Suitability analysis is performed using prob. function in HBMO method. In (10) S(t) is equal to particle speed in PSO method and ∆(f) can be calculated as below: ∆(f ) = gbest(it,:) - particleposition(i) Where gbest(it,:) is the best amount in all conditions and particle position (i) is the present position of the particle. We want to improve voltage profile and reduce power loss in this system by using 1, 2 and 3 DG. Before installation of DG, load flow will be applied. Fig.2 shows voltage profile before DG installation. Fig.3 shows the results of sensitivity analysis. Fig. 2 Voltage profile before installation of DG Fig. 3 Sensitivity of objective function to the location of DG Table 1 Load data BUS P(KW) Q(KVAR) 1 0 0 2 890 468 3 628 470 4 1112 764 5 636 378 6 474 344 7 1342 1078 8 920 292 9 766 498 10 662 480 11 690 186 12 1292 554 13 1124 480 Fig. 4 The 13 bus radial distribution system Table 3 Optimal DG placement and sizing Objective function Voltage variance QL(KVA R) PL(KW) DG size Bus NUMBR of DG --- 0.45 264.01 336.24 0 0 0 Without DG 14.203 0.44 261.61 333.18 147+4.64j 2 1 PSO 15.62 0.43 248.041 315.90 981.72+3.07j 909.71+2.84j 2,11 2 11.88 0.43 243.32 309.86 1335.4+4.2j 278.1+0.9j 550.9+1.7j 2,11,4 3 11.57 0.42 240.68 306.48 1572.3+4.91j 2 1 PSO&HBMO 10.75 0.42 242.041 308.23 1386.60+4.3j 1436.1+4.5j 2,11 2 9.84 0.42 240.42 306.15 1564.9+4.9j 306.8+1j 1313.3+0.4j 2,11,4 3 Table 2 Branch data from to R X 1 2 0.176 0.138 2 3 0.176 0.138 3 4 0.045 0.035 4 5 0.089 0.069 5 6 0.045 0.035 5 7 0.116 0.091 7 8 0.073 0.073 8 9 0.074 0.058 8 10 0.093 0.093 7 11 0.063 0.05 11 12 0.068 0.053 7 13 0.062 0.053 Fig.5 Three DG installing (upper), Without DG (lower)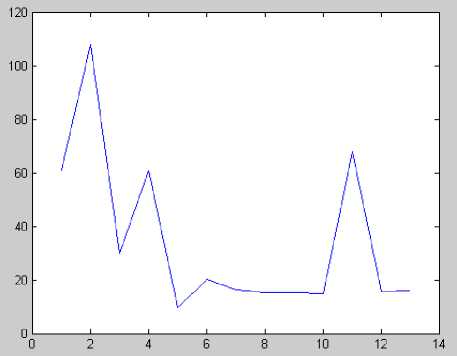
V. PSO&HBMO Procedure
VI. Simulation Results
VII. Conclusions
Список литературы Placement and Sizing of DG Using PSO&HBMO Algorithms in Radial Distribution Networks
- T. Ackermann, G. Anderson, L. Söder; “Distributed Generation: a Definition”, Electric Power System Research, 2001, Vol. 57, pp.195-204.
- P. P. Barker, R. W. de Mello; “Determining the Impact of Distributed Generation on Power Sys-tems: Part 1–Radial Distribution Systems”, IEEE PES Summer Meeting, 2000, Vol.3, pp.1645-1656.
- N. Hadjsaid, J. F. Canard, F. Dumas; “Dispersed Generation Impact on Distribution Networks”, IEEE Compt. Appl. Power, 1999, Vol. 12, pp.22–28.
- W.El-Khattam, M.M.A.Salama; “Distributed Generation Technologies, Definitions and Bene-fits”, Electric Power Systems Research, 2004, Vol. 71, pp.119-128.
- G.Pepermans, J.Driesen, D.Haeseldonckx, R.Belmans, W.D.haeseleer; “Distributed Genera-tion: Definitions, Benefits and Issues”, Energy Policy, 2005, Vol. 33, pp.787-798.
- A.Soroudi, M.Afrasiab; "Binary PSO-Based Dy-namic Multi-Objective Model for Distributed Generation Planning under Uncertainty", IET Re-newable Power Generation, 2012, Vol.6, No. 2, pp. 67 - 78.
- Kai Zou, A.P.Agalgaonkar, K.M.Muttaqi, S.Perera; "Distribution System Planning with Incorporating DG Reactive Capability and System Uncertain-ties" ,IEEE Transactions on Sustainable Energy, 2012, Vol.3 , No.1, pp. 112 – 123.
- Sheng-Yi Su, Chan-Nan Lu, Rung-Fang Chang, G. Gutiérrez-Alcaraz; "Distributed Generation Inter-connection Planning: A Wind Power Case Study ", IEEE Transactions on Smart Grid, 2011, Vol.2 , No.1, pp. 181 – 189.
- Ruifeng Shi, Can Cui, Kai Su, Zaharn Zain; "Comparison Study of Two Meta-heuristic Algo-rithms with their Applications to Distributed Gen-eration Planning", Energy Procedia, 2011, Vol. 12, pp. 245-252.
- A.M. El-Zonkoly; "Optimal Placement of Mul-ti-Distributed Generation Units Including Different Load Models using Particle Swarm Optimization", Swarm and Evolutionary Computation, 2011, Vol.1, No.1, pp. 50-59.
- M.R. AlRashidi, M.F. AlHajri; "Optimal Planning of Multiple Distributed Generation Sources in Distribution Networks: A New Approach", Energy Conversion and Management, 2011, Vol. 52, No. 11, pp. 3301-3308.
- M.H. Moradi, M. Abedini; "A Combination of Genetic Algorithm and Particle Swarm Optimiza-tion for Optimal DG Location and Sizing in Dis-tribution Systems", International Journal of Elec-trical Power & Energy Systems, 2012, Vol.34, No.1, pp. 66-74.
- Qi Kang, Tian Lan, Yong Yan, Lei Wang, Qidi Wu; "Group Search Optimizer Based Optimal Location
- and Capacity of Distributed Generations", Neuro-computing, 2012, Vol.78, No.1, pp. 55-63.
- M. Gomez-Gonzalez, A. López, F. Jurado; "Optimization of Distributed Generation Systems using a New Discrete PSO and OPF", Electric Power Systems Research, 2012, Vol.84, No.1, pp. 174-180.
- R. Srinivasa Rao; "Capacitor Placement in Radial Distribution System for Loss Reduction using Ar-tificial Bee Colony Algorithm", World Academy of Science, Engineering and Technology, 2010, Vol. 68.
- Y. Wang, B. Li, T. Weise, J. Wang , B. Yuan, Q. Tian; “ Self-Adaptive Learning Based Particle Swarm Optimization”, Information Sciences, 2011, Vol.181, No.20, pp. 4515-4538.
- Y. Jiang, T. Hu , C. Huang, X. Wu; “An Improved Particle Swarm Optimization Algorithm”, Applied Mathematics and Computation, 2007, Vol. 193, No.1, pp. 231–239.
- M. Fathian, B.Amiri, A. Maroosi; "Application of Honey-Bee Mating Optimization Algorithm on Clustering", Appl. Math. Comput., 2007, 190(2), pp.1502–1513.
- A. Afshar, O. Bozorg Haddad, M.A. Mariٌo, BJ.Adams; "Honey-Bee Mating Optimization (HBMO) Algorithm for Optimal Reservoir Opera-tion", J. Franklin Inst., 2007, 344(5), pp.452–462.
- T. Niknam; "Application of Honey Bee Mating Optimization on Distribution State Estimation In-cluding Distributed Generators", J. Zhejiang Univ. Sci. A, 2008, 9(12), pp.1753–1764.


