Планирование наблюдений астрономических объектов с космического аппарата с учетом ограничений на моменты выполнения наблюдений

Наряду с наблюдением астрономических объектов с Земли (наземными средствами), большой объем астрономических наблюдений производится с использованием космических аппаратов (КА). Основным преимуществом наблюдений с КА является отсутствие помех от прохождения регистрируемого сигнала через атмосферу Земли. К тому же, наблюдению с КА доступны любые объекты небесной сферы, в то время как возможность выполнения наблюдений с поверхности Земли определяется географической широтой наземных средств наблюдения и не ограничена только при условии размещения средств наблюдения в зоне экватора.

При проведении астрономических наблюдений с КА необходимо учитывать разнообразные условия и ограничения, связанные как с непосредственно целевыми требованиями, так и требованиями, относящимися к функционированию КА, одним из которых является ограничение на затраты ресурсов КА.

В настоящей статье рассматривается задача планирования астрономических наблюдений, исходя из требования минимизации затрат на их выполнение. Задача формулируется следующим образом: требуется построить программу наблюдений астрономических объектов заданного каталога так, чтобы затраты на переход от наблюдения одного объекта к следующему были минимальны [1–3]. Данные затраты могут характеризоваться, например, длительностью переориентации «наблюдателя» (аппаратуры наблюдения/КА) между наблюдениями (в этом случае минимизируется время, не используемое непосредственно для выполнения наблюдений) или расходом требуемых для этого ресурсов. Аппаратура наблюдения может быть как жестко закрепленной на КА, так и установленной на поворотной платформе.

Задача сводится к выбору маршрута: наблюдения начинаются из некоторой начальной точки маршрута (начальное положение аппаратуры наблюдения/ КА), после просмотра всех заданных объектов (каждый — не более одного раза) требуется перейти в конечную точку маршрута (конечное положение аппаратуры наблюдения/КА), при этом искомый маршрут должен удовлетворять требованию прохождения точек маршрута в заданные интервалы времени, определяемые, в т. ч., светотеневой обстановкой на орбите КА, зонами непосредственной видимости объектов с КА, зонами выполнения требуемых ограничений на наблюдения (ограничений на углы между направлениями на астрономические объекты и освещенной Луной, освещенным горизонтом Земли и т. п.).

Формализация и метод решения задачи

Рассматриваем полный ориентированный граф ( V , E ):

V — множество L вершин, включающее N внутренних вершин маршрута { i = 1, …, N } (наблюдаемые объекты) и граничную вершину маршрута { L = N + 1} (пару, содержащую окончание и начало маршрута); E — множество дуг графа {( i , j ) | i , j = 1, …, L ; i ≠ j }. Длина c_ij дуги ( i , j ) составляет затраты на переход от вершины i к вершине j (рис. 1): от объекта i к объекту j , j ≠ i ; от граничной вершины i = L (начало маршрута) к объекту j ; от объекта i к граничной вершине j = L (окончание маршрута); для i = j значение c_ij не определено (доопределяем его как да). Также заданы значения t j длительности времени перехода от вершины i к вершине j .

Требуется найти в графе ( V , E ) кратчайший (сумма длин дуг которого минимальна) гамильтонов цикл ( ГЦ ) — замкнутый маршрут, проходящий через все вершины (каждую — не более одного раза)

ГЦ |min Σ c

| ¹ ГЦ (iJ> C ГЦ V [•                     (1)

При этом искомый маршрут должен удовлетворять следующим ограничениям.

Каждая вершина i = 1, …, L должна быть пройдена в течение заданных интервалов времени Lt-m, t +mJ, m = 1, ..., M. при длительности нахождения в вершине не менее заданного значения Ati. Обозначив ti — время начала прохождения вершин i, i = 1, …, L; t* — время вхождения в граничную вершину L при окончании маршрута, условие прохождения вершин в заданные интервалы времени запишем в виде:

• • для каждой вершины i = 1, …, L существует m = 1, …, M_i такое, что

• t m <  t i ,             t, ^{+ A} t i <  t m ; ;          (2)

• • для граничной вершины L существует m = 1, …, M_L такое, что

• tL. < t*,            t* + AtL < t+„■       (3)

Запишем условия последовательного прохождения вершин маршрута во времени.

Для всех пар внутренних вершин ( i , j ) формулируем следующее требование. Если дуга ( i , j ) входит в маршрут, то вершина j проходится через требуемое время после вершины i :

t_i + A t_i + t j <  t , ,           i , j = 1, ..., N .      (4; )

Для всех пар вершин ( L , j ), начинающихся в граничной вершине и оканчивающихся во внутренних вершинах, формулируем следующее требование. Если дуга ( L , j ) входит в маршрут, то внутренняя вершина проходится через требуемое время после граничной вершины:

t_L + A t_L + t j <  t , ,         j = 1, _, N .      (5; )

Для каждой из пар вершин ( i , L ), начинающихся во внутренних вершинах и оканчивающихся в граничной вершине, формулируем следующее требование. Если дуга ( i , L ) входит в маршрут, то граничная вершина проходится через требуемое время после внутренней вершины, что формализуется условиями

• t , + A t , + t ,L <  t *,           i = 1, ^, N .     (6)

  		Наблюдаемые объекты						Граничная вершина
  		1			j		N	L = N + 1
  8 ^ о S Л ч 2 \о £	1	∞		Затраты на переход				Затраты на переход от объекта к граничной вершине (окончание маршрута)
  			∞	от объекта к объекту
  	i			∞	c ij			c iL
  					∞
  						∞
  	N						∞
  а а	L = N + 1	Затраты на переход от граничной вершины (начало маршрута) к объекту c Lj						∞

  Рис. 1. Матрица затрат { c_ij } для графа (V, E)

  
  

Задача поиска кратчайшего цикла известна как задача коммивояжера . В предложенной постановке маршрут начинается и заканчивается в граничной вершине, введенной с предложенными правилами расчета соответствующих длин дуг (матрицы затрат).

Решение задачи коммивояжера может быть осуществлено, например, по алгоритму Литтла [4], использующему идею метода «ветвей и границ». Алгоритм основан на разделении числа перебираемых вариантов на классы (ветви) с расчетом оценок (границ) для этих классов так, чтобы иметь возможность исключать из дальнейшего рассмотрения ветви, которые не приведут к оптимальному решению. Учет ограничений (2)–(6) на время прохождения вершин искомого маршрута может быть выполнен в ходе итерационного процесса решения задачи путем исключения из дальнейшего рассмотрения тех комбинаций вершин, которые не удовлетворяют данным ограничениям. Алгоритм решения задачи (1)–(6) можно представить в следующем виде.

Принимаем следующие названия: Решение — набор присутствующих и запрещенных в маршруте дуг; Запрет дуги — замена стоимости дуги на ∞; Оценка ( ОЦ ) – нижняя граница стоимости Решения; Главный список ( ГЛСП ) — набор Решений, подлежащих рассмотрению; Рекорд — стоимость кратчайшего из найденных циклов; Приведение матрицы — операция, согласно которой вычитаем последовательно из каждой строки и каждого столбца матрицы их минимальные элементы (при этом вычитаемые константы называем приводящими).

Шаг 1. Текущее Решение R и ГЛСП пусты. Приводим матрицу затрат и вычисляем ОЦ ( R ) как сумму приводящих констант ( СПК ): ОЦ ( R ) = СПК ( R ).

Шаг 2. Элементом ветвления (k, l) Решения R выбираем нулевой элемент приведенной матрицы с максимальным штрафом (штраф вычисляем как сумму наименьших ненулевых элементов строки k и столбца l). Формируем Решение R+ как R с присутствием дуги (k, l), и если оно не удовлетворяет условиям (2)–(6), то исключаем его из дальнейших операций, иначе в R+ запрещаем дуги, присутствие которых приведет к возникновению «внутреннего» цикла, и вычисляем ОЦ(R+) = ОЦ(R) + СПК(R+). Формируем Решение R– как R с запрещением дуги (k, l) и вычисляем ОЦ(R–) = ОЦ(R) + + СПК(R–).

Шаг 3. Берем из ГЛСП Решение R ^ГЛСП с минимальной Оценкой и определяем ОЦ ^min = min{ ОЦ ( R ⁺ ), ОЦ ( R ^– ), ОЦ ( R ^ГЛСП )}. Решение с ОЦ ^min назначаем новым текущим Решением R , ОЦ ( R ) = ОЦ ^min , оставшиеся из Решений R ⁺ , R ^– и R ^ГЛСП добавляем/возвращаем в ГЛСП . Если R — цикл, то идем на Шаг 4 , иначе — на Шаг 2 .

Шаг 4 . Если Рекорд пуст или ОЦ ^min < Рекорд, то Рекорд = ОЦ ^min и удаляем из ГЛСП Решения с Оценкой меньше, чем Рекорд. Если ГЛСП пуст, то Рекорд оптимален, иначе берем из ГЛСП Решение R ^ГЛСП с минимальной Оценкой как новое текущее Решение R , ОЦ ( R ) = ОЦ ( R ^ГЛСП ) и идем на Шаг 2 .

Проблема применения этого и других известных алгоритмов решения задачи коммивояжера состоит в том, что они позволяют учитывать накладываемые ограничения только путем проверки их выполнения для каждого конкретного рассматриваемого Решения, что приводит к необходимости рассмотрения всех в общем случае многочисленных Решений из ГЛСП , оценка которых меньше, чем текущий Рекорд, но которые в дальнейшем будут отброшены как не удовлетворяющие накладываемым ограничениям.

Формализуем задачу для ее решения методами линейного и целочисленного программирования. Вводим бинарные переменные x_ij следующего смыслового значения

1, дуга (i, j) входит в искомый маршрут, xij = 0, в противном случае, xij = (0/1), i, j = 1, …, L; i ≠ j.          (7)

Требуется минимизировать целевую функцию затрат (длину маршрута)

L

Σ x c i, j -1 ij ij

i ≠ j

при выполнении (7) и следующих условий.

Требуется, чтобы в каждой вершине начиналось и заканчивалось по одной дуге маршрута, что формализуется условиями

• LL

Σx = 1, Σx = 1, l = 1, …, L.(9)

j-1 Ij          i-1il j≠li

Требуется исключить из возможных решений циклические последовательности внутренних вершин (циклы, не содержащие граничную вершину), что формализуется условиями xj1 j2 + xj2 j3 + … + xjp–1 jp + xjp j1 < p или p–1

Σ x   + x <  p , j j … j ⊆{ A ( N )},   (10)

г=1 ji ji +1       j p j 1            12 p где {A(N)}

N–1 N!

— множество Σ        разме- p-2 (N - p)!p щений из N по p = 2, …, (N–1) внутренних вершин, в котором последовательности, полученные переходом из начала в конец и из конца в начало ( j1 j2 … jp; j2 … jp j1; …; jp j1 … jp–1), рассматриваются как идентичные.

Ограничения на моменты прохождения вершин формализуются следующим образом. Вводим бинарные переменные ξ _im , ξ* _m следующего смыслового значения

0, время t_i находится в m -ом ξ _im = временном интервале (2),

1, в противном случае,

ξ _im = (0/1), i = 1, …, L ; m = 1, …, M_i ;

Mi

Σ ξ im = M i – 1, i = 1, …, L ;         (11)

m =1

0, время t ^∗ находится в m -ом ξ^∗ _m = временном интервале (3),

1, в противном случае,

ξ _m * = (0/1), m = 1, …, M_L ;

^M Σ ^L ξ _m * = M_L – 1.           (12)

m=1

С учетом данных переменных условия (2), (3) записываются в виде t–im– ti ≤ MAξim, ti + Δti – t+im≤ MAξim, i = 1, …, L; m = 1, …, Mi;          (13)

t– – t* ≤ M ξ*, t* + Δt – t+ ≤ M ξ*, Lm            A m,          L Lm A m, m = 1, …, ML.                (14)

Величина M A > max { t m - t i ; t i + A t i - t + _m ;

t ^– _Lm – t *; t * + Δ t_L – t ⁺ _Lm } рассчитывается как величина, превышающая максимальные значения, которые могут принимать левые части данных неравенств. Использование M_A позволяет обеспечить безусловное выполнение неравенств при ненулевых значениях бинарных переменных ξ , ξ*. im m

Условия последовательного прохождения вершин маршрута во времени (4)–(6) с учетом того, что согласно условию (9) для одного из j x_lj = 1, а для остальных j x_lj = 0; для одного из i x_il = 1, а для остальных i x_il = 0, записываем в следующем виде:

t_i + Δ t_i + t_ij – t_j ≤ M_B (1 – x_ij ), i, j = 1, …, N , (15) t_L + Δ t_L + t_Lj – t_j ≤ M_B (1 – x_Lj ), j = 1, …, N , (16) t_i + Δ t_i + t_iL – t * ≤ M_B (1 – x_iL ), i = 1, …, N . (17)

Величина M_B >  m _i, a _j x { t_i + Δ t_i + t_ij – t_j } рассчитывается как величина, превышающая максимальные значения левых частей данных неравенств. Использование M_B обеспечивает безусловное выполнение неравенств при нулевых значениях бинарных переменных x_ij .

Cформулированная задача минимизации целевой функции (8) при условиях (7), (9)–(17) является частично-целочисленной задачей линейного программирования и решается методами линейного и целочисленного программирования [5, 6]. Особенностью задачи является существенное количество ограничений (10), обеспечивающих исключение «внутренних» циклов. Отметим, что при решении задачи (1)–(6) с использованием алгоритма Литтла исключение «внутренних» циклов осуществляется проверкой на каждом шаге ветвления задачи возможности их образования и исключением из рассмотрения дуг, включение которых в текущее Решение приведет к возникновению «внутреннего» цикла.

Примеры построения оптимальных последовательностей наблюдения астрономических объектов с КА

Рассмотрим планирование наблюдений с орбитального КА астрономических объектов заданного каталога, например, 13 наиболее ярких звезд из созвездий Близнецов, Возничего, Малого и Большого Пса, Ориона, Тельца (табл. 1).

Наблюдения выполняются на теневой части орбиты. Затраты на переориентацию аппаратуры наблюдения/КА от наблюдения одного объекта к другому характеризуем угловым расстоянием между объектами. Требуется построить программу наблюдений так, чтобы затраты на переориентацию от наблюдения очередного объекта к последующему были минимальны [1–3].

Таблица 1

Каталог астрономических объектов

№ п/п	Названия звезд	Координаты звезд
		а, °	8, °
1	Бета Ориона (Ригель)	78,45	–8,22
2	Альфа Возничего (Капелла)	78,89	45,98
3	Гамма Ориона (Беллатрикс)	81,08	6,34
4	Бета Тельца (Эльнат)	81,34	28,60
5	Дзета 1 Ориона (Альнитак)	85,00	–1,95
6	Альфа Ориона (Бетельгейзе)	88,59	7,41
7	Бета Возничего (Менкалинан)	89,61	44,95
8	Гамма Близнецов (Альхена)	99,21	16,41
9	Альфа Большого Пса (Сириус)	101,12	–16,69
10	Эпсилон Большого Пса (Адара)	104,51	–28,95
11	Бета Большого Пса (Мирцам)	110,88	–29,27
12	Альфа Близнецов (Кастор)	113,41	31,92
13	Альфа Малого Пса (Порцион)	114,63	5,26

Полагаем, что исходная и конечная ориентации аппаратуры наблюдения/ КА совпадают с ориентацией для наблюдения рассматриваемых объектов. Требуется начать наблюдения из исходной ориентации аппаратуры наблюдения/КА, совпадающей с ориентацией для наблюдения одного из объектов, и закончить наблюдения в конечной ориентации аппаратуры наблюдения/КА, также совпадающей с ориентацией для наблюдения одного из объектов. В этом случае матрица затрат не зависит от дат полета.

Наблюдения выполняем с околокру-говой орбиты типа орбиты орбитальной космической станции с параметрами: высота околокруговой орбиты ≈410 км, наклонение орбиты 51,64°; на момент прохождения восходящего узла орбиты 01.02.2017 г. 23:57:52,42 (ДМВ) долгота восходящего узла орбиты в инерциальной системе координат Q = 352,9°.

Возможные интервалы времени L t^- ; t +m J, m = 1, …, M_i выполнения наблюдений определяются зонами видимости объектов на теневой части витков орбиты.

Значение требуемой длительности наблюдения объектов A t (считаем ее одинаковой для всех объектов) выбираем с учетом длительности теневых участков орбиты на рассматриваемом интервале полета КА. Например, в интервале дат 22.08…28.10.2017 г. длительность T теневых участков орбиты составляет 22–36 мин, что соответствует максимальным значениям A t 1,7-2,8 мин (A t <  T/N , N = 13).

Рассмотрим планирование наблюдений для вариантов значений требуемой длительности наблюдения объектов A t =1,5 мин и 2 мин; длительности L перехода от объекта к объекту определяем как отношение углового расстояния между объектами к скорости поворота/пере-ориентации наблюдателя (аппаратуры наблюдения относительно КА или непосредственно самого КА), принимаемой равной 180 °/мин. Считаем, что возможное время успокоения после переориентации входит в величину A t .

Задачу решаем в формулировке (1)–(6), используя описанный алгоритм, полученный на основе алгоритма Литтла. В табл. 2 представлены полученные для различных дат полета КА длины S кратчайших маршрутов с указанием даты, долготы Q восходящего узла орбиты в инерциальной системе координат на момент начала витка, значения угла в между направлением на Солнце и плоскостью орбиты КА, продолжительности T теневого участка витка и требуемой длительности наблюдения объектов A t .

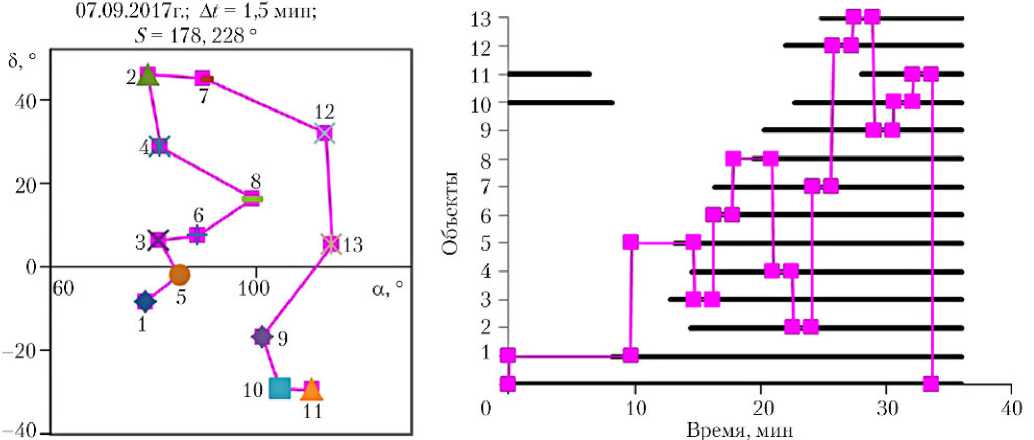
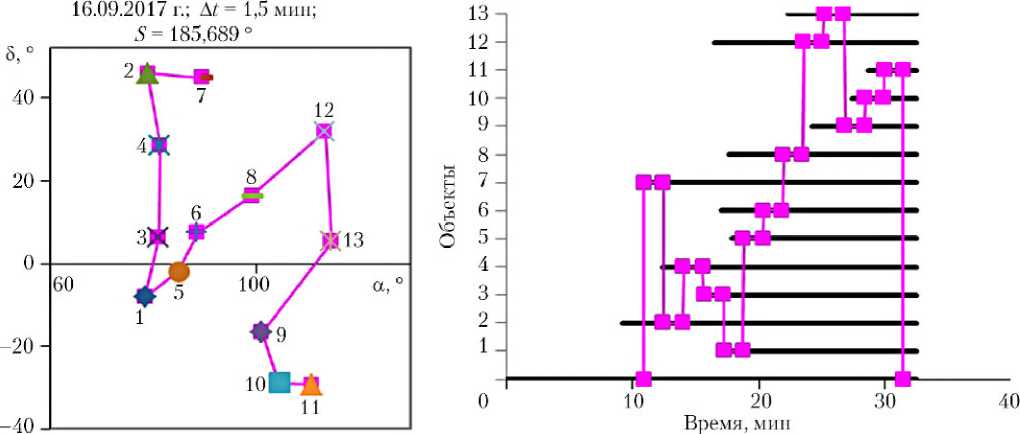
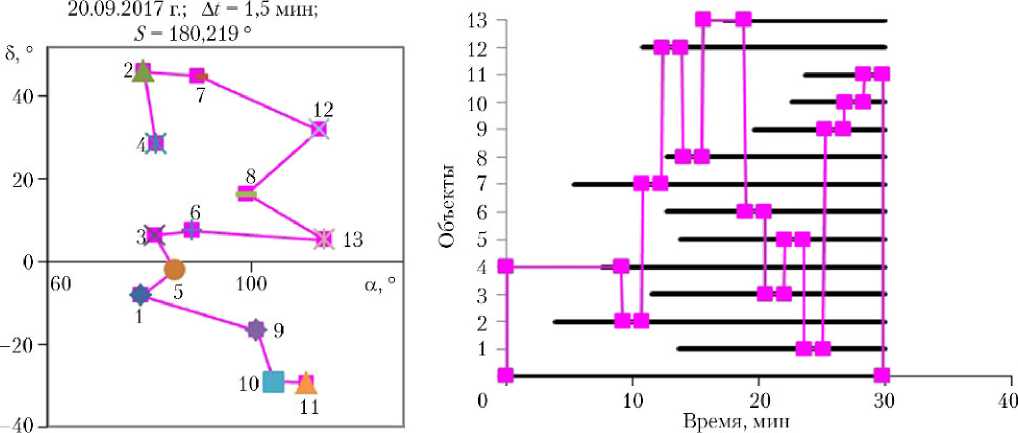
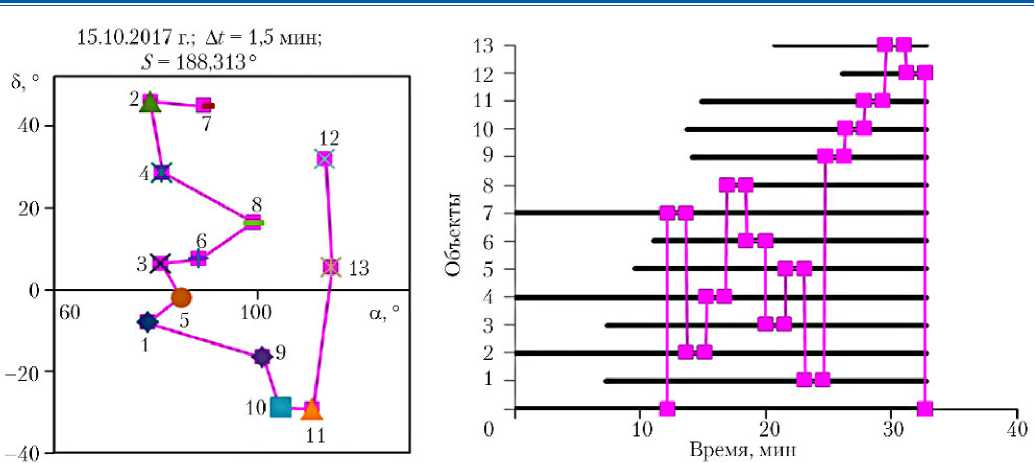
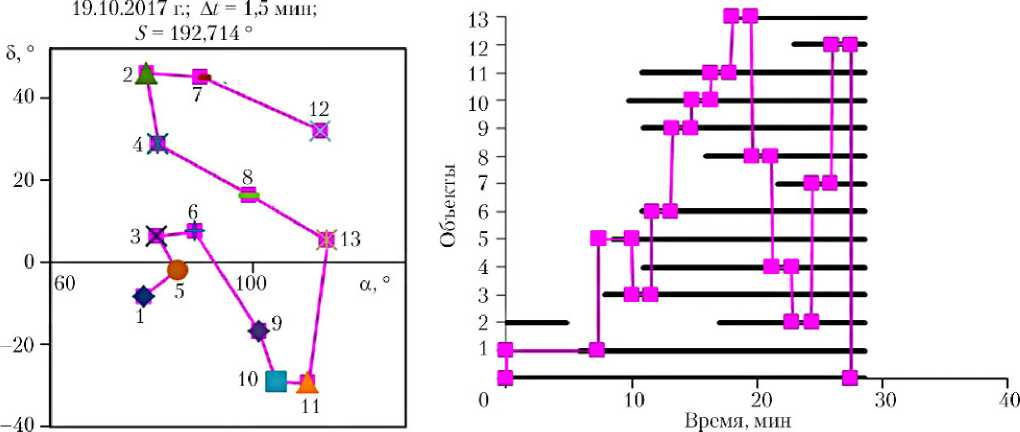
На рис. 2 представлены примеры кратчайших маршрутов наблюдения объектов: в левой части рисунков на карте звездного неба показаны маршруты наблюдения объектов с указанием даты, требуемой длительности наблюдения объектов A t и длины маршрута S ; в правой части рисунков по вертикальной оси указаны номера объектов/вершин, по горизонтальной оси отображена шкала времени от начала теневого участка, относительно которой показаны интервалы видимости объектов на теневом участке и последовательность переориентаций аппаратуры наблюдения/КА из исходной ориентации (граничная вершина под номером 0) через ориентацию для наблюдения каждого из объектов (внутренние вершины под номерами объектов 1–13) в конечную ориентацию (возврат в граничную вершину под номером 0).

a)

б)

в)

г)

д)

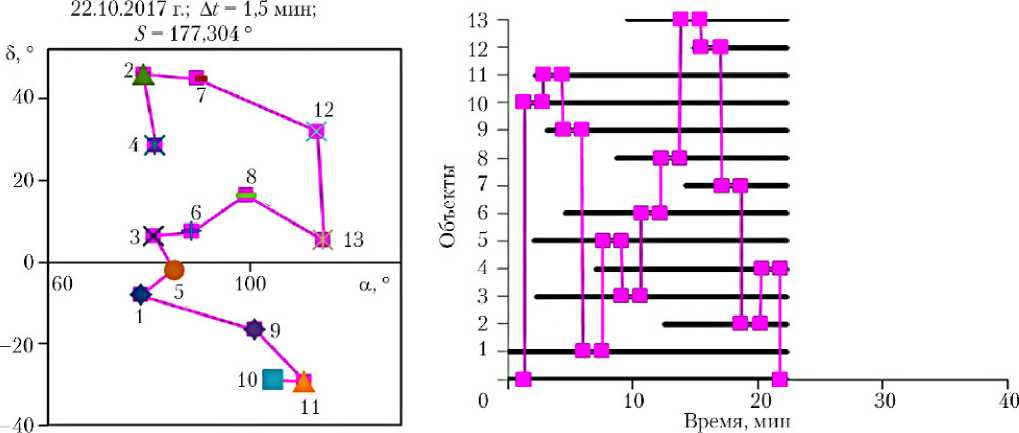
Рис. 2. Кратчайшие маршруты наблюдения объектов

е)

Таблица 2

Длины кратчайших маршрутов наблюдения объектов с КА

Дата	П °	р. °	T , мин	5 , °; A t = 1,5 мин	5 , °; A t = 2 мин
22.08.2017 г.	69,4	–39,4	32,8	176,20	^^^^~ 3
25.08.2017 г.	53,4	–40,0	32,6	174,51	174,51
28.08.2017 г.	37,4	–34,6	33,6	174,51	174,51
31.08.2017 г.	21,4	–24,9	34,9	174,51	174,51
04.09.2017 г.	5,3	–12,5	35,7	174,51	174,51
07.09.2017 г.	349,3	1,1	36,0	178,23 (рис. 2, а )	198,00
10.09.2017 г.	333,3	15,2	35,6	185,82	^^^^~ 3
13.09.2017 г.	317,2	28,8	34,5	185,82	^^^^~ 3
16.09.2017 г.	301,2	40,9	32,4	185,69 (рис. 2, б )	^^^^~ 3
20.09.2017 г.	285,2	49,4	30,0	180,22 (рис. 2, в )	^^^^~ 3
23.09.2017 г.	269,1	51,5	29,1	174,51	180,22
26.09.2017 г.	253,1	46,1	31,1	174,51	174,51
29.09.2017 г.	237,1	35,4	33,5	174,51	174,51
06.10.2017 г.	205,0	6,9	35,9	174,51	174,51
12.10.2017 г.	173,0	–24,2	34,9	178,23	178,23
15.10.2017 г.	156,9	–39,3	32,8	188,31 (рис. 2, г )	188,63
19.10.2017 г.	140,9	–52,7	28,6	192,71 (рис. 2, д )	^^^^~ 3
22.10.2017 г.	124,9	–61,9	22,3	177,30 (рис. 2, е )	^^^^~ 3
25.10.2017 г.	108,8	–62,1	22,1	174,51	^^^^~ 3
28.10.2017 г.	92,8	–53,3	28,3	174,51	174,51

Представленные результаты показывают, что для рассмотренного примера длина кратчайшего маршрута изменяется в зависимости от даты полета в пределах ~10% от минимально возможного значения. При этом на всем рассмотренном интервале дат полета на теневой части витка можно реализовать последовательное наблюдение всех объектов каталога с длительностью наблюдения каждого объекта не менее At = 1,5 мин, в то время как для значения At = 2 мин в определенные даты полета такой возможности не существует. Отметим, что возможность наблюдения объектов для At = 2 мин отсутствует как в даты с продолжительностью теневого участка менее 26 мин, недостаточной для реализации двухминутных наблюдений 13 объектов, так и в даты, когда теневой участок орбиты имеет достаточную продолжительность, но реализуется «неудачное» относительное расположение зон видимости объектов (не существует маршрута, обеспечивающего последовательное наблюдение объектов с длительностью наблюдения объекта > At, в то время как все объекты по отдельности доступны наблюдению длительностью At). Естественно, на более широком интервале дат может также не существовать как возможности наблюдения по крайней мере одного из объектов (видимость объекта на теневом участке орбиты менее At), так и самого теневого участка («солнечная» орбита при больших значениях |р|).

Заключение

Разработанный подход к решению задачи планирования наблюдений астрономических объектов с КА обеспечивает возможность построения оптимальных программ наблюдения объектов с учетом наложения ограничений на моменты выполнения наблюдений. Предложенный подход учета указанных ограничений охватывает формулировки в виде задачи коммивояжера и в виде частично-целочисленной задачи линейного программирования.

Представленные примеры построения оптимальных программ наблюдений астрономических объектов заданного каталога с КА иллюстрируют возможность практического использования предложенного подхода, в т. ч. на интервалах полета с изменяющейся светотеневой обстановкой на орбите КА. Описанные примеры показывают эффективность применения предложенного подхода как для построения оптимальных программ наблюдения, так и для анализа условий и определения возможных параметров для реализации наблюдений.