Plato on being, time, and recollection

In dialogues such as the Timaeus and the Sophist it is argued that Being is both non-spatial and non-temporal. Despite this, spatiotemporal terminology is used to describe Being. For example, in the Sophist Being is discussed as if it were an entity that emerges or appears in the midst of an inquiry. As will be explained below, thinking and reasoning operate within the realm of becoming. Consequently, the distinction between Being on the one hand, and our reasoning about it on the other, is easily overlooked.

Below I argue that Plato has two ways of reasoning about Being, each of which avoids the error of characterizing Being as a spatiotemporal entity. First, instead of excising spatiotemporal terms from descriptions of Being, in some dialogues Plato takes the opposite approach: he presents an image (εἰκών) that depicts Being as if it were a spatiotemporal entity. More specifically, he uses “well-wrought” images that indicate features of Being by way of contrast. Second, where a higher-order form of reasoning is needed, he uses the concept of the one and its relation to ἀριθμός as an analogue for reasoning about Being: as Being communes with

everything that is, one is a part of every number. Being and ἀριθμός are both foundational in Plato’s thought. The latter serves as a lens through which Being can be conceived.

Reasoning by means of images on the one hand, and reckoning in terms of ἀριθμός on the other, are not mutually exclusive. Rather, they are complementary; Plato sometimes presents an image of a whole to portray that which is neither spatial nor temporal. Such an image is determined by a conceptual structure that joins many into one. Focusing on both the Sophist and the Meno, below I will argue that the theory of recollection presents such an image.

2.    Imaginary Spaces in the Meno and the Sophist

As is the case with many of Plato’s dialogues, reasoning in both the Meno and the Sophist is often expressed by means of spatial metaphors. For example, the quest for a definition of the sophist is articulated as a pursuit in an imaginary space. The following passage is typical of the language used by Plato throughout the Sophist :

ΞΕ. Δέδοκται τοίνυν ὅτι τάχιστα διαιρεῖν τὴν εἰδωλοποιικὴν τέχνην, καὶ καταβάντας εἰς αὐτήν, ἐὰν μὲν ἡμᾶς εὐθὺς ὁ σοφιστὴς ὑπομείνῃ, συλλαβεῖν αὐτὸν κατὰ τὰ ἐπεσταλμένα ὑπὸ τοῦ βασιλικοῦ λόγου, κἀκείνῳ παραδόντας ἀποφῆναι τὴν ἄγραν· ἐὰν δ' ἄρα κατὰ μέρη τῆς μιμητικῆς δύηταί πῃ, συνακολουθεῖν αὐτῷ διαιροῦντας ἀεὶ τὴν ὑποδεχομένην αὐτὸν μοῖραν, ἕωσπερ ἂν ληφθῇ. πάντως οὔτε οὗτος οὔτε ἄλλο γένος οὐδὲν μή ποτε ἐκφυγὸν ἐπεύξηται τὴν τῶν οὕτω δυναμένων μετιέναι καθ' ἕκαστά τε καὶ ἐπὶ πάντα μέθοδον.

Stranger: So it’s settled. We’ll divide the craft of copy-making as quickly as we can and we’ll go down into it. Then if the sophist gives up right away we’ll obey the royal command and we’ll capture him and hand our catch over to the king. But if the sophist slips down somewhere into the parts of the craft of imitation, we’ll follow along with him and we’ll divide each of the parts that contain him until we catch him. Anyway, neither he nor any other kind will ever be able to boast that he’s escaped from the method of people who are able to chase a thing through both the particular and the general. (235b-c) 1

Here, Plato describes an imaginary space in which the Eleatic Stranger and Theaetetus “go down” (καταβαίνω) into a part of copy-making in pursuit of their quarry, the sophist — an imaginary figure who repeatedly evades them. Preceding the passage above the Stranger states: “σχεδὸν γὰρ αὐτὸν περιειλήφαμεν ἐν ἀμφιβληστρικῷ τινι τῶν ἐν τοῖς λόγοις περὶ τὰ τοιαῦτα ὀργάνων” (“We’ve almost hemmed [the sophist] in with one of those net-like devices that words provide for things like this.”2; 235a-b). In this way, Plato presents the quest for a definition as a pursuit in which the Stranger and Theaetetus gradually close in on the sophist. Shorey observes that in the same dialogue, the paradigmatic definition of the angler “is a summation of all the right-hand distinctive or differentiating qualifications” — qualifications that are imagined to be arranged as kinds and sub-kinds in a “logical tree.”3

The spatial metaphors of the Sophist are paralleled in the Meno . For example, both Socrates and Meno suggest that one must “search” (συζητέω) in the hope that one can “meet with” (ἐντυγχάνω) virtue (80d-e). Socrates states that the slave boy can find knowledge within himself (85d) — for the truth is always “ἐν τῇ ψυχῇ” (“in the soul”; 86b). Here, memory is depicted as a kind of space within the soul, a space in which truths may be found and “met with.”

Spatial metaphors are employed throughout Plato’s dialogues. In the Phaedrus , μανίας (madness) is divided into two parts: a “left-hand” (σκαιόν) part and a “right-hand” (δεξιᾷ) part (266a). In the Symposium , a lover gains knowledge by turning toward “the great sea of beauty” (“τὸ πολὺ πέλαγος τετραμμένος τοῦ καλοῦ”; 210d). In the Republic , the image of the Cave and the divided line are even more explicit in their use of spatial metaphors.

In his essay on the Greek verb ‘to be’ and the concept of Being, Kahn states:

It is not merely that Greek thought was instinctively concrete: the very notion of being had local connotations. And so Plato, when for the first time he clearly introduced non-spatial entities into a philosophical theory, was careful to situate his new Forms in a new kind of place. What we are in the habit of calling the “intelligible world” is presented by Plato quite literally as an intelligible region or place, the νοητòς τόπος, conceived by analogy with the region known to sense-experience, but sharply contrasted with it, in order to serve as the setting for Plato’s radically new view of Being.⁴

Hence, even non-spatial entities, the Forms, are described with “local connotations” — i.e., they are imagined to be in an intellectual space or a “νοητòς τόπος.”

Thinking appears to be structured — i.e., ordered and coherent — when it is imagined to take place in a space with clear-cut divisions. This is seen in both the Meno and the Sophist. In the former, a drawing articulates geometric divisions. In the latter, Plato’s metaphorical distinction between left and right determines the directions in which reasoning about the sophist proceeds. We see this at 264d-e, for example, where the Stranger proposes dividing image-making into two kinds: “Πάλιν τοίνυν ἐπιχειρῶμεν, σχίζοντες διχῇ τὸ προτεθὲν γένος, πορεύεσθαι κατὰ τοὐπὶ δεξιὰ ἀεὶ μέρος τοῦ τμηθέντος, ἐχόμενοι τῆς τοῦ σοφιστοῦ κοινωνίας . . .” (“let’s try again to take the kind we’ve posited and cut it in two. Let’s go ahead and always proceed through the right-hand part of what we’ve cut, and hold onto things that the sophist is associated with . . .”5). Here, reasoning “proceeds” (πορεύω) through the parts of an imaginary space in which each part represents a kind or sub-kind that distinguishes the sophist from others. The directions in which thought moves determine the definition of the sophist; to an extent, reasoning in the Sophist is not unlike tracing a path on a tree diagram, where each node or part of the tree visually indicates a clearly-defined concept.6

In the dialogues, space serves as the setting in which thought moves. Each step in an argument is a step that requires time. This much is evident in any dialogue. But in several dialogues Plato highlights the fact that thinking moves by picturing an imaginary space in which the steps of reasoning take place. Just as the sophist can be hunted in an imaginary space and gradually hemmed in (235b) — so long as one follows the correct lines of thought — so too one can “ascend” (ἐπάνειμι) in stages to behold Beauty ( Symposium 211b), or one can treat memory as a space in which truths are sought ( Meno 86b).

In the Sophist , one can only “proceed” (πορεύω) through an imaginary space during a stretch of time; the very idea of a chase in which an elusive quarry is hunted conjures an image of time as well as space. This is reflected throughout the dialogue. For example, when reasoning reaches an impasse, Theaetetus describes the sophist as follows: “φαίνεται γὰρ οὖν προβλημάτων γέμειν, ὧν ἐπειδάν τι προβάλῃ, τοῦτο πρότερον ἀναγκαῖον διαμάχεσθαι πρὶν ἐπ᾽αὐτὸν ἐκεῖνον ἀφικέσθαι” (“He seems to have a whole supply of roadblocks, and whenever he throws one down in our way we have to fight through it before we can get to him.”⁷; 261a). Here, as in many other passages, a spatial metaphor contains a temporal allusion; an obstacle (πρόβλημα) is something that reasoning must work its way through before it can progress to a conclusion.

In the following section I will argue that while both spatial and temporal metaphors can add poetic and philosophical value to a dialogue, they can subtly undermine attempts to conceptually grasp Being and other non-spatiotemporal entities — just as sophistry is represented by an individual located in an imaginary space, Being is assumed to be an object of knowledge that emerges at some point in time.

3.    Being, Space, and Time

In the Meno and the Sophist , spatial and temporal metaphors add poetic value to the dialogues. To the extent that they clarify what is being said, they also add philosophical value. For example, when the Stranger states that the sophist is in a place of darkness while the philosopher is in a place of light (254a-b), we know that he is speaking metaphorically. The contrast between light and dark highlights the difference between the sophist and the philosopher. The claim that the sophist and the philosopher are opposites may be a claim that we disagree with, but at least the Stranger is making his claim clear.

In the Sophist , Being itself is described in spatiotemporal terms. For example, Theaetetus and the Stranger consider whether rest and motion are “embraced” (περιέχω) by Being (250b). The term περιέχω is also used in the Meno at 85a when Socrates asks if the diagonals embrace or contain the area of the double square (“Οὐκοῦν τέτταρες αὗται γίγνονται γραμμαὶ ἴσαι, περιέχουσαι τουτὶ τὸ χωρίον;”). Thus, the claim that Being “embraces” or “surrounds” rest and motion brings to mind the image of a geometric figure — Being is spatialized in the mind’s eye.

The assumption that Being — or anything that is — must be located or extended in space is prevalent in ancient thought. Kahn states:

We have from Presocratic times the well-established axiom that whatever is, is somewhere; what is nowhere is nothing . . . As Plato puts it (stating not his own view, but that of Greek common sense), “we say that it is necessary for everything which is real (τὸ ὂν ἅπαν) to be somewhere in some place and to occupy some space, and that what is neither on earth nor anywhere in heaven is nothing at all” ( Tim . 52B). If existence and location are not identical in Greek thought, they are at least logically equivalent, for they imply one another. That is, they do for the average man, and for the philosophers before Plato.⁸

In the same essay, Kahn also states that when what is is expressed in a “locative sense” — i.e., a sense in which there is an allusion to place or location — it “inevitably tends to be conceived as thing-like rather than as fact-like.”9 Being, when conceived in spatial terms, seems to be an entity or object in space that must be sought and discovered. In Plato’s dialogues, we see this not only with reasoning about Being, but with reasoning about kinds. For example, the Sophist reifies a kind, sophistry, into an individual, the sophist, and as an entity or creature of the imagination, a space is constructed for him. The sophist is chased and found to be in a place (τόπος) of darkness, while the philosopher — another reification — is found to be in a place of light (254a). The underlying assumption is that without his own imagined “place,” the sophist cannot be clearly distinguished from others. Similarly, as explained above, Plato distinguishes Being from rest and motion using a spatial metaphor — Being is that which surrounds or embraces the latter.

Hence, spatial reasoning about kinds (e.g., sophistry, virtue, madness, Beauty ) carries over to reasoning about Being. But in Plato’s view, neither the Forms nor Being are spatial. When we reason about space and entities that are located in space, we are not reasoning about Being. The Timaeus describes reasoning about space as follows:

τρίτον δὲ αὖ γένος ὂν τὸ τῆς χώρας ἀεί, φθορὰν οὐ προσδεχόμενον, ἕδραν δὲ παρέχον ὅσα ἔχει γένεσιν πᾶσιν, αὐτὸ δὲ μετ' ἀναισθησίας ἁπτὸν λογισμῷ τινι νόθῳ, μόγις πιστόν, πρὸς ὃ δὴ καὶ ὀνειροπολοῦμεν βλέποντες καί φαμεν ἀναγκαῖον εἶναί που τὸ ὂν ἅπαν ἔν τινι τόπῳ καὶ κατέχον χώραν τινά, τὸ δὲ μήτ' ἐν γῇ μήτε που κατ' οὐρανὸν οὐδὲν εἶναι.

And the third type is space, which exists always and cannot be destroyed. It provides a fixed state for all things that come to be . It is itself apprehended by a kind of bastard reasoning that does not involve sense perception, and it is hardly even an object of conviction. We look at it as in a dream when we say that everything that exists must of necessity be somewhere, in some place and occupying some space, and that that which doesn’t exist somewhere, whether on earth or in heaven, doesn’t exist at all. (52a-b)¹⁰

Space provides us with a kind of dream-like conviction. It provides the foundation for that which becomes (“γένεσιν πᾶσιν”), not Being.

In addition to the locative aspect, Kahn argues that there is another aspect of the verb εἶναι, the “durative aspect.”11 He states that this aspect is “inseparable from the stem” of the verb, and “it colors every use of the verb, including every philosophical use. Whatever the real entities are for a philosopher, these are the entities which endure.”12

The contrast between Being and becoming is a hallmark of Plato’s philosophy. But for Plato at least, Being does not “endure”; endurance implies extension in time. But just as Being is not extended in space, it is not extended in time. The Timaeus describes the non-temporal nature of Being as follows:

ἡμέρας γὰρ καὶ νύκτας καὶ μῆνας καὶ ἐνιαυτούς, οὐκ ὄντας πρὶν οὐρανὸν γενέσθαι, τότε ἅμα ἐκείνῳ συνισταμένῳ τὴν γένεσιν αὐτῶν μηχανᾶται· ταῦτα δὲ πάντα μέρη χρόνου, καὶ τό τ' ἦν τό τ' ἔσται χρόνου γεγονότα εἴδη, ἃ δὴ φέροντες λανθάνομεν ἐπὶ τὴν ἀίδιον οὐσίαν οὐκ ὀρθῶς. λέγομεν γὰρ δὴ ὡς ἦν ἔστιν τε καὶ ἔσται, τῇ δὲ τὸ ἔστιν μόνον κατὰ τὸν ἀληθῆ λόγον προσήκει, τὸ δὲ ἦν τό τ' ἔσται περὶ τὴν ἐν χρόνῳ γένεσιν ἰοῦσαν πρέπει λέγεσθαι—κινήσεις γάρ ἐστον, τὸ δὲ ἀεὶ κατὰ ταὐτὰ ἔχον ἀκινήτως οὔτε πρεσβύτερον οὔτε νεώτερον προσήκει γίγνεσθαι διὰ χρόνου οὐδὲ γενέσθαι ποτὲ οὐδὲ γεγονέναι νῦν οὐδ' εἰς αὖθις ἔσεσθαι, τὸ παράπαν τε οὐδὲν ὅσα γένεσις τοῖς ἐν αἰσθήσει φερομένοις προσῆψεν . . .

At the same time as he framed the heavens, he devised their coming to be. These all are parts of time, and was and will be are forms of time that have come to be. Such notions we unthinkingly but incorrectly apply to eternal Being. For we say that it was and is and will be , but according to the true account only is is appropriately said of it. Was and will be are properly said about the becoming that passes in time, for these two are motions. But that which is always changeless and motionless cannot become either older or younger in the course of time — it neither ever became so, nor is it now such that it has become so, nor will it ever be so in the future. And all in all, none of the characteristics that becoming has bestowed upon the things that are borne about in the realm of perception are appropriate to it. These, rather, are forms of time that have come to be¹³ . . . (37e-38a)

Given the above, reasoning that rests on the assumption that Being is in time or in space is erroneous — space and time apply to becoming, not Being. Being does not even endure or grow older — only that which is in time can do so. Yet, in Plato’s dialogues Being is sometimes treated as an entity that appears and recedes. For example, in the Sophist, the Stranger states: “τὸ δὲ ὂν ἡμῖν νῦν ἐκτὸς τούτων ἀμφοτέρων ἀναπέφανται.” — Being “appears to fall outside” both motion and rest (250d). The term ἀναφαίνω means to show forth, to come out, or reappear14; Fowler translates this word as “emerge.”15 The same term is also used at 250e in reference to both Being and not-Being when the Stranger states: “νῦν ἐλπὶς ἤδη καθάπερ ἂν αὐτῶν θάτερον εἴτε ἀμυδρότερον εἴτε σαφέστερον ἀναφαίνηται, καὶ θάτερον οὕτως.” (“Now there is hope that just as one of them shows forth, either brightly or dimly, the other will also.”). While an image of Being may emerge in the mind’s eye and appear to be bright or dim, Being itself cannot — it cannot emerge at all, given that it is non-temporal and non-spatial. But the distinction between Being on the one hand, and our images or thinking about Being on the other, is missing in remarks such as these.

Summarizing page 248a of the Sophist and similar passages in the Phaedo and the Theaetetus , Guthrie states: “we are in touch with Becoming by means of the body through sensation, and with real Being by means of the mind ( psyche ) through reason . . .”¹⁶ Clearly, the body and its perceptions change, and Plato does not indicate otherwise. However, thought too is in motion. In the Sophist , thought in the form of speech is described as a “stream” (“ῥεῦμα”) that flows from the soul (263e).

Diotima’s remarks in the Symposium elaborate on the close connection between thought, knowledge, and becoming. She states that feelings and opinions are always coming to be in the soul and passing away (207e); not only this, but the same is true of knowledge:

πολὺ δὲ τούτων ἀτοπώτερον ἔτι, ὅτι καὶ αἱ ἐπιστῆμαι μὴ ὅτι αἱ μὲν γίγνονται, αἱ δὲ ἀπόλλυνται ἡμῖν, καὶ οὐδέποτε οἱ αὐτοί ἐσμεν οὐδὲ κατὰ τὰς ἐπιστήμας, ἀλλὰ καὶ μία ἑκάστη τῶν ἐπιστημῶν ταὐτὸν πάσχει. ὃ γὰρ καλεῖται μελετᾶν, ὡς ἐξιούσης ἐστὶ τῆς ἐπιστήμης· λήθη γὰρ ἐπιστήμης ἔξοδος, μελέτη δὲ πάλιν καινὴν ἐμποιοῦσα ἀντὶ τῆς ἀπιούσης μνήμην σῴζει τὴν ἐπιστήμην, ὥστε τὴν αὐτὴν δοκεῖν εἶναι.

And what is still far stranger than that is that not only does one branch of knowledge come to be in us while another passes away and that we are never the same even in respect of our knowledge, but that each single piece of knowledge has the same fate. For what we call taking thought of (μελετάω) exists because knowledge is leaving us, because forgetting is the departure of knowledge, while thought puts back a fresh memory in place of what went away, thereby preserving a piece of knowledge, so that it seems to be the same.¹⁷ (207e-208a)

These remarks make it clear that both thinking and knowledge are in the realm of becoming and change.

The above claims give rise to the following question: how can we harmonize the fact that thinking changes and becomes, while that which thinking aims for — the truth, or that which is — does not? Being is not located anywhere; hence, thought cannot move toward or away from it. Only metaphorically can thought “turn toward” what is. Insofar as Being is concerned, thinking cannot even “miss the mark” (Sophist 228c-d), as this too implies that Being is located somewhere, and that with the right line of thinking, it is only a matter of time before one can encounter it. But Being is not a target that can be hit or missed, nor does it emerge or appear to us as an object of knowledge at some point in time — appearance applies only to things that are in time and space.

Below I will argue that Plato employs two ways of reasoning that avoid implicitly characterizing Being as a spatiotemporal entity. First, he uses images that are contrasted with Being, but highlight certain features of it. Second, ἀριθμός (number, arithmetic) serves as a non-spatiotemporal analogue of Being.

4.    Images and Αριθμός: Two Ways of Reasoning about Being

Given that thinking and knowledge are in the realm of becoming, one may argue that the very nature of thinking and reasoning leads us astray, insofar as Being is concerned. However, Plato takes advantage of the fact that the ways in which we think about Being are precisely what Being is not. This is especially the case when he employs images that are explicit — i.e., images that are clearly contrasted with the realities they purport to represent.

An example of such an image is presented by the Athenian Stranger in the Laws . At 897d, he employs the image of a lathe to answer the question, “What is the nature of the motion of reason?” (“Τίνα οὖν δὴ νοῦ κίνησις φύσιν ἔχει;”):

ΑΘ. Μὴ τοίνυν ἐξ ἐναντίας οἷον εἰς ἥλιον ἀποβλέποντες, νύκτα ἐν μεσημβρίᾳ ἐπαγόμενοι, ποιησώμεθα τὴν ἀπόκρισιν, ὡς νοῦν ποτε θνητοῖς ὄμμασιν ὀψόμενοί τε καὶ γνωσόμενοι ἱκανῶς· πρὸς δὲ εἰκόνα τοῦ ἐρωτωμένου βλέποντας ἀσφαλέστερον ὁρᾶν.

Athenian: Still, in answering this question we mustn’t assume that mortal eyes will ever be able to look upon reason and get to know it adequately: let’s not produce darkness at noon, so to speak, by looking at the sun direct. We can save our sight by looking at an image of the object we’re asking about. (897d-897e) ¹⁸

Here, an image (εἰκών) serves as a means by which we can reason about the motion of reason — it is a device by means of which an elusive concept can be represented. Such a figurative device is necessary because if we “look” directly at reason, while paradoxically using reason itself to do so, we are in danger of being blinded, as if looking directly at the sun. In other words, a reasoner cannot “step outside” of reason to examine the shape and motions of reason – to do so would require an abandonment of reason. For this reason, an image is used as a device

Anthony M. Pasqualoni /ΣΧΟΛΗ Vol. 16. 2 (2022) 559 not unlike a schematic or diagram that allows us to see, albeit indirectly, the answer to the question.

Equally important is the fact that the image is skillfully made or constructed. At 898a-b the Athenian Stranger explains how the motion of reason can be understood as the revolution of the turning wheels of a lathe. He states that by using this image to understand the motions of reason, a skillful use of “beautiful images by means of reasoning” (“λόγῳ καλῶν εἰκόνων”) is being employed:

ΑΘ. Τὸ κατὰ ταὐτὰ δήπου καὶ ὡσαύτως καὶ ἐν τῷ αὐτῷ καὶ περὶ τὰ αὐτὰ καὶ πρὸς τὰ αὐτὰ καὶ ἕνα λόγον καὶ τάξιν μίαν ἄμφω κινεῖσθαι λέγοντες, νοῦν τήν τε ἐν ἑνὶ φερομένην κίνησιν, σφαίρας ἐντόρνου ἀπεικασμένα φοραῖς, οὐκ ἄν ποτε φανεῖμεν φαῦλοι δημιουργοὶ λόγῳ καλῶν εἰκόνων.

Athenian: Take reason on the one hand, and motion in a single location on the other. If we were to point out that in both cases the motion was determined by a single plan and procedure and that it was regular; uniform; always at the same point in space; around a fixed center; in the same position relative to other objects; and were to illustrate both by the example of a sphere being turned on a lathe, then no one could ever show us up for incompetent makers of beautiful images by means of reasoning. (898a-b)19

The reference to motion around a fixed center tells us how the motions of reason are arranged in a metaphorical space. By seeing the motions as spherical, the placement of each part of the image is made clear, as if each part were arranged as a point on a geometric figure or as the part of a schematic. In short, an image wrought by reason (λόγος) clarifies the structure of an object or phenomenon that is difficult, if not impossible, to conceive by means of reason alone.

A useful image is an image that does not hide the fact that it is only an image. A geometric drawing in the sand, for example, is honest in this way. It is not pretentious; it accepts its ephemeral nature, and it has no qualms about its irregularities and distortions; it does not hide them. Verbal images and metaphors that are subtle and hard to notice tend to mislead us. For this reason, an image that is well-wrought, as in the case of the image of the lathe, is one that is explicitly an image.

Plato also crafts images that aid us in reasoning about Being. In the Sophist , the Stranger states the following about Being and its relation to philosophy: “Ό δέ γε φιλόσοφος, τῇ τοῦ ὄντος ἀεὶ διὰ λογισμῶν προσκείμενος ἰδέᾳ, διὰ τὸ λαμπρὸν αὖ τῆς χώρας οὐδαμῶς εὐπετὴς ὀφθῆναι· τὰ γὰρ τῆς τῶν πολλῶν ψυχῆς ὄμματα καρτερεῖν

πρὸς τὸ θεῖον ἀφορῶντα ἀδύνατα.” (“But the philosopher always uses reasoning to stay near the form, Being . He isn’t at all easy to see because that area is so bright and the eyes of most people’s souls can’t bear to look at what’s divine.”²⁰; 254a-b). Here the image of Being is not unlike the image of reason in the Laws . That which is difficult to grasp conceptually is indicated by way of an image. If the image is well crafted, it tells us something about that which it represents in a manner that is clearly figurative. In this case, it is evident that Being itself is not visible. But the image of intense and divine brightness tells us that Being is too much of a reality to be apprehended directly, at least for most of us. This is not unlike the image of the sun in the allegory of the Cave; at first, one can only see its reflection in the water, given its intensity ( Republic 516a-b).

In his dialogues Plato presents temporal as well as spatial images. For example, the theory of recollection as presented in the Meno rests on an image of time as well as space. More specifically, the theory inverts the idea that a search aims to find what is sought in the future: rather, the theory tells us that what is sought was found in the past; instead of looking outward for something not yet here, one must look inward to find something that one already has: “ἀεὶ ἡ ἀλήθεια ἡμῖν τῶν ὄντων ἐστὶν ἐν τῇ ψυχῇ” — the truth of that which is is always in our soul ( Meno 86b). By means of a contrasting temporal image — an immense stretch of time that extends into the deep past — the convergence of past and present, and the atemporal nature of that which is , is indicated. This is paralleled by the image of Being described above. Being is invisible, yet Plato inverts this idea with an image in which Being is not only visible, but brilliant — it is so bright that it blinds us ( Sophist 254a-b). In the Meno, the image of a vast stretch of time which contains ancient truths is used to indicate that which is timeless — i.e., an atemporal reality is represented with a temporal image. In the Sophist , the image of a visible phenomenon — a blinding light — is used to depict a reality that is invisible. The contrast between image and reality, when made explicit, is a means by which Plato overcomes the difficulties of describing a non-spatiotemporal reality.

While Plato makes good use of what may be called “teaching images,” images suffer from limitations that call for an alternative form of reasoning. Insofar as images teach us anything about Being, they can do so only indirectly, and by way of contrast. The Eleatic Stranger in the Statesman states that while sensible images can serve as teaching devices (277b-c), the greatest beings (μεγίστοις οὖσι) can be adequately understood “by reason only” (“λόγῳ μόνον”) rather than through an image (“εἴδωλον”) (285e-286b). For these reasons, there is a need for reasoning about Being that is of a higher order. Below I will argue that ἀριθμός — number, arithmetic, counting21 — provides another way to reason about Being, a way that eschews the limitations of images.

Just as Being is a whole that is interrelated with all that is ( Sophist 259a), ἀριθμός is a whole whose parts are interrelated; there is no number that is not related in manifold ways to every other number. For example, three is greater than two; four is greater than three; four is double two, ad infinitum . Equally important, numerical relations — e.g., lesser and greater, half and double — are non-spatial and non-temporal, insofar as they are strictly numerical — it is their applications, for example in geometry, that may be spatial or temporal.

The primacy of one relative to two and the remaining integers is analogous to Being and its primacy relative to all that is. Just as Being communes (συμμίγνυμι) with everything that is ( Sophist 259a), one is a part of every number. For this reason, in the Parmenides one is used to construct the set of integers. Parmenides states: “Εἰ ἄρα ἔστιν ἕν, ἀνάγκη καὶ ἀριθμὸν εἶναι.” — if one (ἕν) is, necessarily number ( ἀριθμός) is as well (144a). Since each integer is one (143d), one is the foundation or basis of ἀριθμός.²² In more general terms, Parmenides states: “Πρὸς ἅπαντι ἄρα [ἑκάστῳ] τῷ τῆς οὐσίας μέρει πρόσεστιν τὸ ἕν, οὐκ ἀπολειπόμενον οὔτε σμικροτέρου οὔτε μείζονος μέρους οὔτε ἄλλου οὐδενός.” (“...oneness is attached to every part of Being and is not absent from a smaller or a larger, or any other, part”²³; 144c).

Just as the one defines each part of a whole, it also defines the whole of which the parts are members. The Parmenides makes it clear that a whole is one: “τὸ ὅλον τὸ ἕν ἐστιν” (145c). Moreover, as the Stranger in the Sophist states, everything that is or comes to be is a single whole ( Sophist 245d). A whole is one even if it has parts; i.e., even if it is a quantity: “Καὶ μὴν οὐδ' ὁποσονοῦν τι δεῖ τὸ μὴ ὅλον εἶναι· ποσόν τι γὰρ ὄν, ὁπόσον ἂν ᾖ, τοσοῦτον ὅλον ἀναγκαῖον αὐτὸ εἶναι.” (“And moreover something that isn’t a whole can’t be of any quantity at all, since something that’s of a certain quantity has to be a whole of that quantity, whatever it may be.”²⁴; 245d). Hence, without the one, neither parts nor wholes can exist as such.

When a whole has parts, each part is considered to be one part. More specifically, there are limits between the parts themselves and between the parts and the whole. The limits of a part define the part as a part. This is explained in the following passage from the Parmenides , where Parmenides describes to

Socrates the process by which parts are formed through the imposition of unity on the indeterminate (ἄπειρον):

Καὶ μὴν ἐπειδάν γε ἓν ἕκαστον μόριον μόριον γένηται, πέρας ἤδη ἔχει πρὸς ἄλληλα καὶ πρὸς τὸ ὅλον, καὶ τὸ ὅλον πρὸς τὰ μόρια ... Τοῖς ἄλλοις δὴ τοῦ ἑνὸς συμβαίνει ἐκ μὲν τοῦ ἑνὸς καὶ ἐξ ἑαυτῶν κοινωνησάντων, ὡς ἔοικεν, ἕτερόν τι γίγνεσθαι ἐν ἑαυτοῖς, ὃ δὴ πέρας παρέσχε πρὸς ἄλληλα…

And whenever each part comes to be one part, the parts then have a limit in relation to each other and in relation to the whole, and the whole has a limit in relation to the parts … Accordingly, it follows for things other than the one that from the one and themselves gaining communion with each other, as it seems, something different comes to be in them, which affords a limit for them in relation to each other²⁵…(158c-158d)

This passage describes the formation of parts and the limits between them when the unlimited or the indeterminate (ἄπειρον) coheres into a whole. In Verity Harte’s terms, it describes the formation of a “composition” or “structure.”26 In epistemological terms, conceptual boundaries or demarcations between the parts of a conceptual whole define the structure of the whole: to the extent that parts are borderless — i.e., lacking in limit — structure and coherence are lacking. In other words, the well-defined parts of a whole define the whole as an intelligible structure. In the following section I will argue that the theory of recollection presents an image of such a structure.

5.    Conclusion

To summarize the above, Plato responds to the fact that thinking and reasoning are in the realm of becoming in two ways. First, he uses explicit images that indicate, by way of contrast, truths about realities that are neither spatial nor temporal. Second, he employs ἀριθμός — number and arithmetic — as an analogue for that which is ; just as one is the basis of ἀριθμός, Being unifies all that is. In this section, I will argue that these ways of reasoning, though different in kind, are not mutually exclusive. Rather, they are complementary — they can work in tandem. More specifically, Plato sometimes employs an image of a whole — a picture of a single , coherent structure — to describe an elusive concept. I will argue below that the theory of recollection is such an image.

In the Parmenides passage discussed above, it is stated that the one communes (κοινωνέω) with that which is other than it; it gives form and structure to a whole and its parts (see Section 4). In the Meno , the idea of a structured whole — i.e., a single family of cognate truths — plays a key role in the theory of recollection. Socrates states “φύσεως ἁπάσης συγγενοῦς οὔσης” (81c-d). This has been translated as “the whole of nature is akin”²⁷ or “all nature is akin,”²⁸ but Socrates is not talking about nature per se. In addition to nature , the term φύσεως (genitive form of ‘φύσις’) also means origin or creation.²⁹ The wide scope of Socrates’ claim is made evident in a preceding remark: “ἑωρακυῖα καὶ τὰ ἐνθάδε καὶ τὰ ἐν Ἅιδου καὶ πάντα χρήματα” (81c) — the soul has “seen” (ὁράω) all things, not only in life, but also in death — i.e., in the underworld. Given that what follows these remarks is a lesson in geometry, it must be the case that Socrates is not referring to truths about nature. Rather, he is referring to primordial truths — e.g., mathematical truths — and their coalescence into a single family.

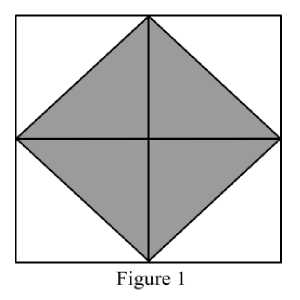
Socrates’ claims tell us that what appears to be a multiplicity is in fact a unity. In other words, πάντα χρήματα — all things30 — are joined together; i.e., they are “συγγενής” (akin; cognate). Although reasoning and recollection do not reveal the whole at once, a single truth can lead to other truths, and together they can at least indicate the whole, if not reveal it. Socrates states: “ἁπάσης συγγενοῦς οὔσης, καὶ μεμαθηκυίας τῆς ψυχῆς ἅπαντα, οὐδὲν κωλύει ἓν μόνον ἀναμνησθέντα — ὃ δὴ μάθησιν καλοῦσιν ἄνθρωποι — τἆλλα πάντα αὐτὸν ἀνευρεῖν, ἐάν τις ἀνδρεῖος ᾖ καὶ μὴ ἀποκάμνῃ ζητῶν· τὸ γὰρ ζητεῖν ἄρα καὶ τὸ μανθάνειν ἀνάμνησις ὅλον ἐστίν.” (“Since all is akin, and the soul has learned everything, nothing prevents a man, after recalling one thing only — a process men call learning — discovering everything else for himself, if he is brave and does not tire of the search, for searching and learning are, as a whole, recollection.”31; 81d). In Socrates’ geometry lesson we are shown that the discovery of one truth leads to another, and ultimately a single solution is found: each diagonal of the four two-unit squares, when placed into a structured whole, reveals the solution to the problem of the double square (fig. 1).

Reasoning and ἀριθμός are intimately connected in Plato’s dialogues. The word that Plato uses for ‘counting’ — λογισμός — is the same word used to express both recollection and reasoning about Being. At Sophist 254a, it is stated that the philosopher always devotes himself through λογισμός to the idea of Being (“τῇ τοῦ ὄντος ἀεὶ διὰ λογισμῶν προσκείμενος ἰδέᾳ”). The word λογισμός means counting, arithmetic, and numbers as well as reason or argument³²; hence , it is closely associated with ἀριθμός. In the Meno we see how this term is used in the sense of counting when Socrates states to the slave boy: “Πόσοι οὖν εἰσιν οἱ δύο δὶς πόδες; λογισάμενος εἰπέ.” (“How many feet is twice two feet? Count and tell me.”³³; 82d). Later in the same dialogue Socrates describes recollection itself with this term — recollection is “αἰτίας λογισμῷ” (98a) — “explanatory reason.”

For the reasons given above, images that are “well wrought” — e.g., the image of the lathe in the Laws — play a key role in Plato’s dialogues. I believe the theory of recollection as described in the Meno presents such an image, and it is an image that portrays memory as a single family of truths: the truths that are in the soul are not isolated facts; rather, they are interwoven into an intelligible whole.

Recollection as presented in the Meno is a series of steps that culminate in a single solution. It is not unlike the “binding” (συνδέω) that concludes the Sophist (268c). Here, the Stranger and Theaetetus engage in “winding up from the end to the beginning” (“τοὔνομα συμπλέξαντες ἀπὸ τελευτῆς ἐπ' ἀρχήν”) the parts of the definition of the sophist. The many names that describe him are bound into one name; what had seemed to be many threads of reasoning, or many lines of thought, converge into one definition. Similarly, in Socrates’ geometry lesson, what at first appeared to be a multiplicity of squares and line segments reveals itself as a single figure — the many become one. In this way, Socrates presents an image of memory that is the antithesis of the claim that learning and knowledge are in constant flux (Symposium 207e-208a; see Section 3). Instead, recollection unveils a stable structure; it is as if the thinking and reasoning of the past have crystallized into a static whole.

One can argue that memory is very different from its portrayal in the Meno — there is reason to believe that memory is nebulous and ephemeral. Against Plato, one may claim that memory in general is an indeterminate mass of isolated truths, or a collection of beliefs that fade over time and become distorted, not unlike a wax block with imprints that blend into each other and become blurred (cf. Theaetetus 194e-195a). But the theory of recollection paints a very different picture. Memory is not indeterminate, nor does it fade in time; memories are ordered into a whole that reveals the kinship of all that is. In other words, memory has an architecture — it is a structure that can be searched out; parts of it may be discovered and brought to light. In this sense, the crystal-clear solution to the geometry problem, with its interconnected elements, is an image of memory.

According to the Parmenides, the parts of an intelligible whole have limits, and it is the limits between the parts themselves and between the parts and the whole that determine a structure (158c-158d; see Section 4). This is what we see with the geometric figure in the Meno (fig. 1). The four diagonals of the two-unit squares establish limits between the inner square and the area that encompasses it; in this way, the parts of a whole — the sides of the inner square — establish a single, determinate structure. Out of a multiplicity of line segments, one figure comes to light.

The unity of the geometric figure is an analogue for the ordered whole of timeless truths that is the foundation of recollection. In this way, the geometric figure produced during the geometry lesson can be understood as an image or icon of memory. Just as the image of the lathe depicts reason in a poetic fashion ( Laws 897d-897e; see Section 4), the geometric figure depicts memory in a mathematical fashion.

Given the above, thinking about Being is analogous to remembering: Being may appear to be something that is sought and discovered, but it is always present. The difficulty is that at any particular point in time, we are not aware of it as a whole. But our limited awareness deceives us. This is the key message of the geometry lesson in the Meno: what may appear to be unrelated and divided, such as the diagonals of the two-unit squares, are in fact related. Seemingly isolated truths, when seen correctly, join into one. When we extend this lesson, we realize that the Meno and the Sophist center on one subject — ultimately these two dialogues are not about the things that are or the things that were or even a truth yet to be discovered, but simply what is — an eternal whole, a timeless one. This is true of any dialogue, insofar as it concerns that which truly is. For Plato, to be is to be one and whole and always present — Being is not many, not divided, and it is not temporal. The many, the divided, and the temporal belong to the realm of becoming (Timaeus 37e-38a, Sophist 245d). A dialogue that reveals manifold relations and relata as an undivided whole that is present, and always present, is a dialogue that indicates something about Being.

In the Sophist , the Stranger states that Being communes or joins (συμμίγνυμι) with all that is (259a; see Section 4). Regardless of whether we imagine a community of all that is, or a single family of cognate truths as described in the Meno , Being is that which joins the many into one. To use an analogy, just as the double square in the Meno joins each of the diagonals together into a whole, Being joins each member of what is into a single community, a one. Despite appearances, this joining is neither in space nor in time.³⁴