Плазмон-поляритонные волны в цилиндрических направляющих структурах

Известно [1], что поверхностные плазмон-по-ляритонные волны (ПППВ) могут возникать на границе сред, имеющих противоположные по знаку значения диэлектрических проницаемос-тей. Важным признаком этих волн является то, что они должны обязательно обладать продольной составляющей вектора напряженности электрического поля, максимум которой находится на границе раздела сред. Их также отличает отсутствие продольной составляющей напряженности магнитного поля, то есть это волны Е-типа (или ТМ-волны). Известно также [1], что благородные металлы обладают отрицательной действительной частью диэлектрической проницаемости на частотах ниже частоты плазмонного резонанса. Достаточно много работ посвящено исследованию характеристик ПППВ, возникающих в направляющих наноструктурах, и использованию их свойств в различных функциональных устройствах, таких как сенсоры [2], элементы интегральных схем [3], оптические модуляторы и переключатели [4; 5], элементы интерферометров [6].

Хорошо изучены свойства ПППВ в планарных многослойных структурах с металлическими нанопленками [7; 8]. В настоящей работе приведены результаты исследований свойств волн, по-видимому, имеющих сходное происхождение, в цилиндрических направляющих структурах: круглый металлический наностержень (рис. 1, а) и круглый диэлектрический волновод с металли- ческой нанопленкой (рис. 1, б). Такие структуры могут быть использованы, например, в качестве элементов наносенсоров и наноантенн [9; 10]. Однако, как будет показано в статье, исследование полей указанных волн приводит к выводу, что их следует называть просто плазмон-поля-ритонными волнами (ППВ), не употребляя к ним термин «поверхностные».

Спецификой данной работы, как и некоторых прежних работ авторов статьи по данной тематике [11; 12], является то, что исследование ППВ производится с учетом реальных свойств металлов в оптическом диапазоне, что является строгим подходом к решению задачи и вскрывает многие принципиальные физические результаты.

Известно [1; 13], что диэлектрическая проницаемость благородных металлов в оптическом диапазоне является комплексной величиной:

s ( to ) = s r ( to ) + i б i ( to )                                    (1)

Частотные зависимости действительной и мнимой частей диэлектрической проницаемости благородных металлов в оптическом диапазоне в соответствии с теорией Друде – Зоммерфельда записываются следующим образом [1; 13]:

Б r ( to ) = Б r о - to p J to ;                                (2)

Б i ( ^to ) = б i о ^+rto p /^to 3 ,                                ⁽³⁾

где to p = 4 n n e e ² / m e « 1.43 ■ 10 16 с ¹ — плазмонная частота электронного газа; б r о — константа,

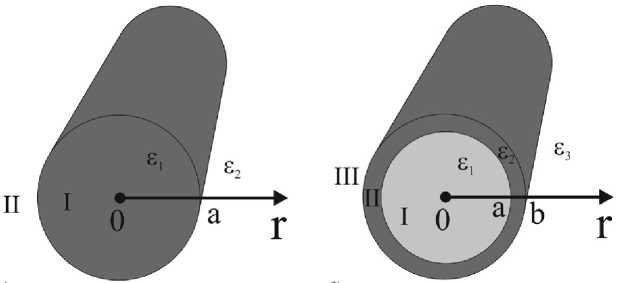
Рис. 1

учитывающая межзонные переходы в металле, обычно варьируется от 1 до 10; Г — коэффициент затухания, учитывающий радиационные потери ( Г ® 10¹⁴ с ^{- 1}), 8 i о = 0.

Одним из авторов данной статьи был разработан метод нахождения комплексных решений транцендентных уравнений [14], основанный на известном из теории функции комплексного переменного методе вариации фазы [15]. Позднее авторами статьи был разработан комбинированный метод поиска комплексных корней трансцендентных уравнений [16], сочетающий в себе положительные качества метода вариации фазы и метода Мюллера [17]. Комбинированный метод позволяет использовать быстроту нахождения комплексных корней методом Мюллера и однозначность идентификации комплексного корня методом вариации фазы. Суть комбинированно- го метода состоит в том, что комплексная плоскость поиска решения разбивается на небольшие подобласти, в которых методом вариации фазы определяется наличие корня, а потом методом Мюллера этот корень уточняется. Либо сначала методом Мюллера находится решение, а потом методом вариации фазы подтверждается истинность найденного решения.

Рассмотрим круглый металлический наностержень (рис. 1, а). Дисперсионное уравнение для такой структуры выглядит следующим об- разом:

8 1 J ( a a )   8 2 H p) ^(а 2 a )

---------:------:--------------- = 0, а1 J0 (а1a )  а 2 H2) (а2a )

где J0 – функция Бесселя; H0(2) – функция Хан-келя 2-го рода; а1 2 — поперечные волновые числа первой и второй, которые связаны с продоль- ным волновым числом в = Р1 + i02 соотношением

⁸ 1,2 ^ 1,2 ^ю = ^а 1,2 ^{+ в} .

Как известно [1], в металлической нанопроволоке ППВ существуют на частотах ниже частоты плазмонного резонанса. Выше этой частоты

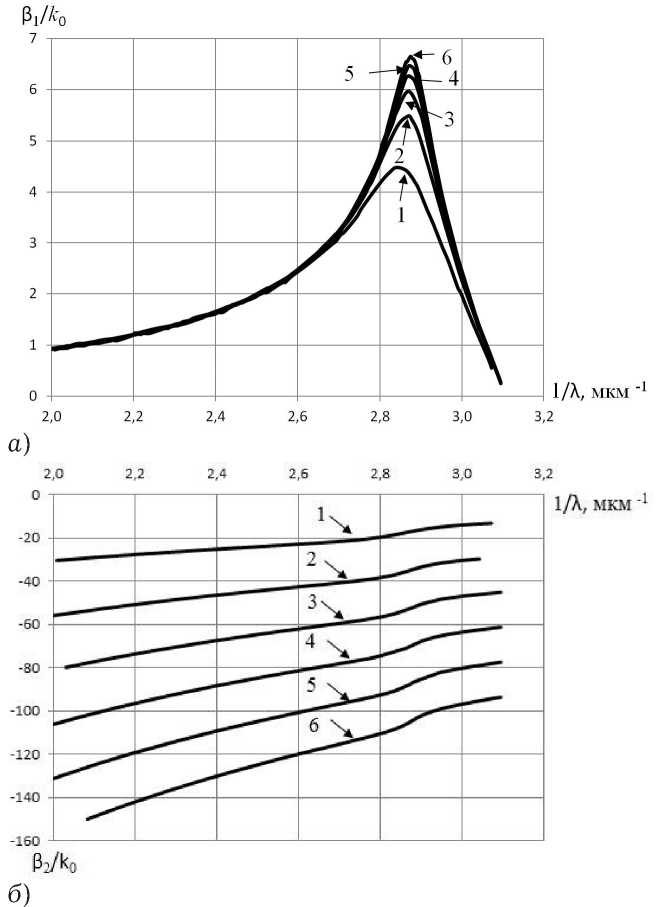
Рис. 2

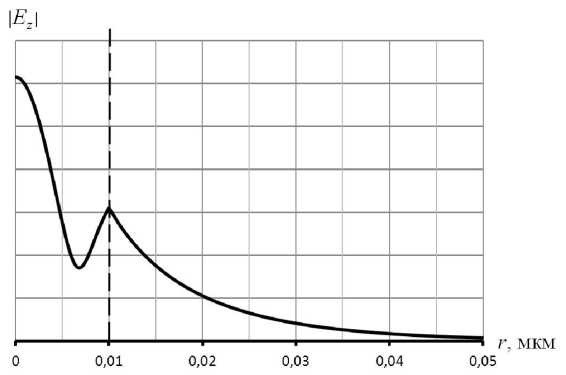
Рис. 3

б )

Рис. 5

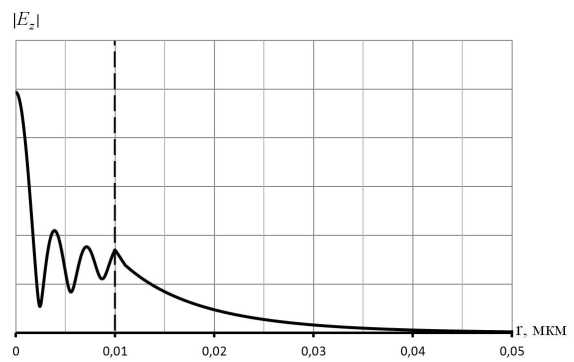
Рис. 4

характеристики затухания шести первых ППВ для металлического стержня, радиус которого a = 110 нм. Видно, что затухание волн в стержне такого радиуса значительно (почти на порядок) меньше, чем для стержня радиуса a = 10 нм. Отмеченное уменьшение затухания связано, видимо, с тем, что при большем радиусе стержня поле более медленно убывает во внешней среде, то есть в меньшей степени сконцентрировано в металле, материал которого обладает потерями.

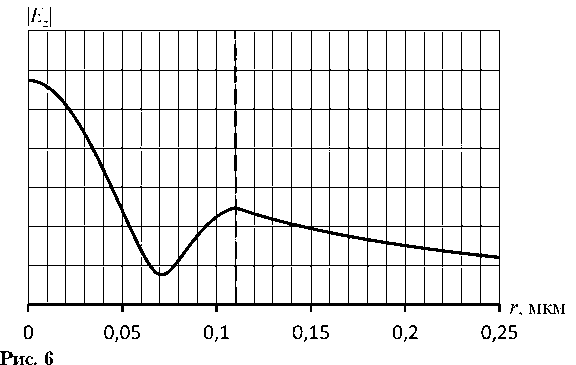
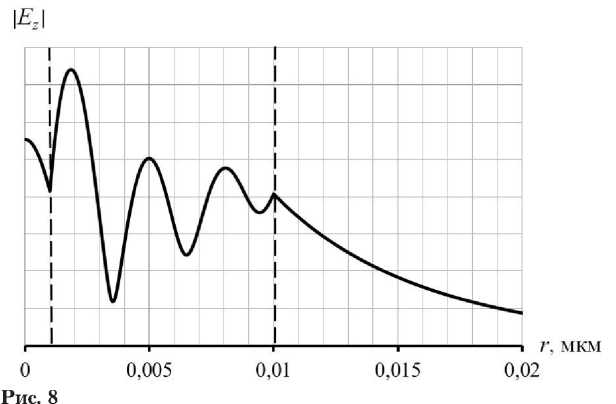
На рис. 6 для примера приведено распределение модуля компоненты поля E_z от координаты r для волны с индексом 1 в точке 1 λ ≈ 2,9 мкм - ¹; β 1 k 0 ≈ 0,26; β 2 k 0 ≈ - 1,83.

Рассмотрим спектр ППВ в диэлектрическом волноводе с металлической нанопленкой, рис. 1, б .

Для данной электродинамической структуры для случая Е-волн ставится краевая задача на уравнении Гельмгольца для продольной составляющей электрического вектора Герца:

А П Z + 8цю 2 П Z = 0. (6)

Решения уравнения Гельмгольца для каждой из трех областей запишем в виде:

I область (диэлектрический стержень)

Π ^e _{z 1} = A 1 J 0 ( α 1 r ) e - ⁱ β ^z ; (7)

1/Л, мкм

3,2

II область (металлическая пленка)

П12 = [ A-Jo («2r)+ B2Yo (a2r)] e-i"1 ;(8)

III область (внешняя бесконечная среда)

П13 = A3H® («3r)e-iв 1,(9)

где « 12 3 — поперечные волновые числа первой, второй и третьей областей, которые связаны с продольным волновым числом в соотношением:

£1,2,3^1,2,3Ю2 = а2,2,3 + в2 ;(10)

J ₀, Y ₀ – функции Бесселя первого и второго рода; H ₀⁽²⁾ – функции Ханкеля второго рода. Для второй области (нанопленка) диэлектрическая проницаемость металла на оптических частотах рассчитывается по формулам (1)–(3).

Выражаем тангенциальные компоненты электрического и магнитного полей через вектора Герца и подставляем их в граничные условия:

E¹ 1 l r = a = E¹ 2 r = a ; H Ф 1 | _r = a = H Ф2 | _r = a ;

E 1 2 | _r = b = E 1 3 | _r = b ^; H ф1 | r = b = H ф2 | r = b •

В результате образуется система из четырех линейных уравнений относительно неизвестных амплитудных коэффициентов A ₁, A ₂, B ₂, A ₃. Дисперсионное уравнение получается из условия нетривиальности решения системы. Дисперсионное уравнение решаем совместно с соотношениями, связывающими волновые числа (10).

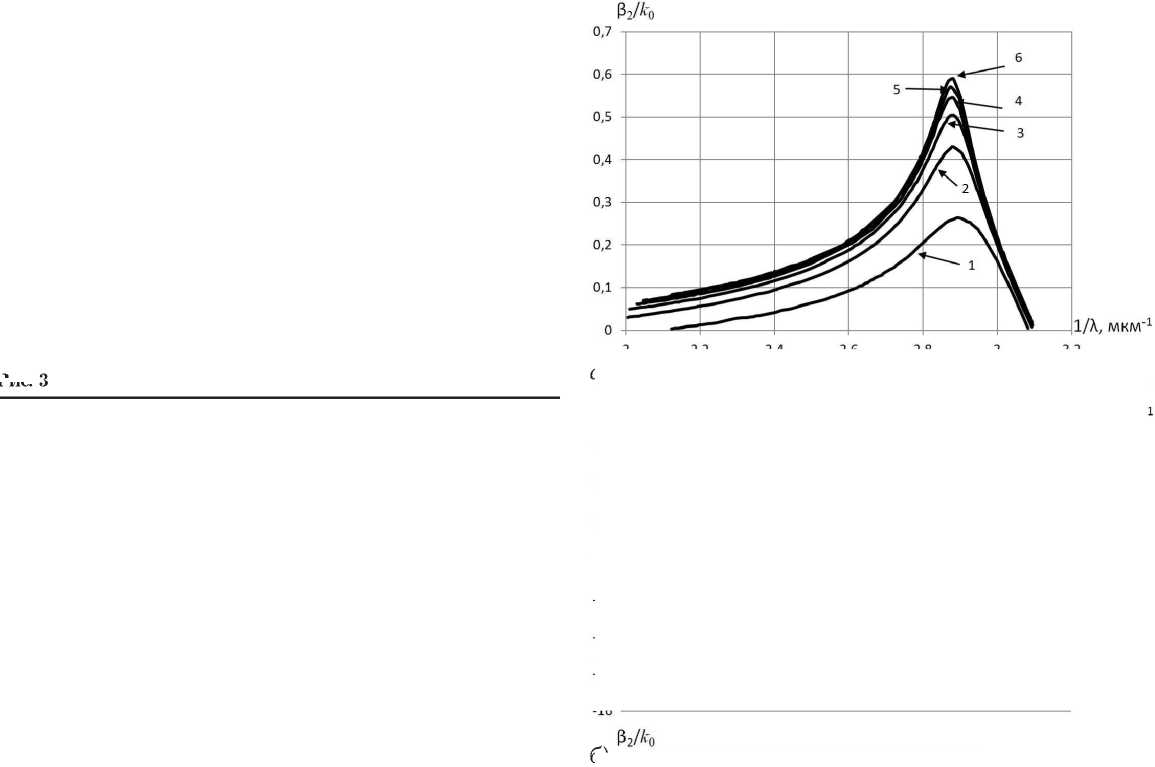
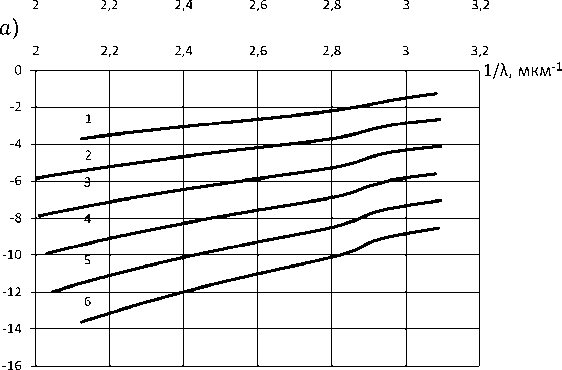
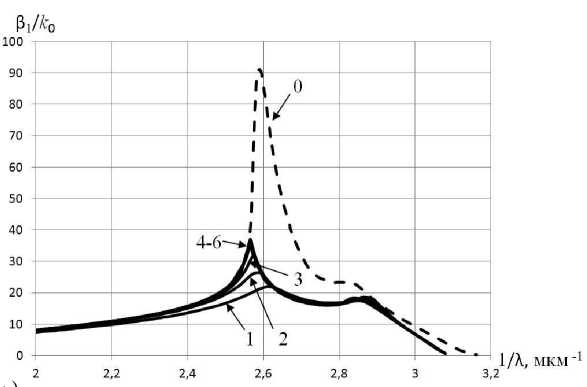
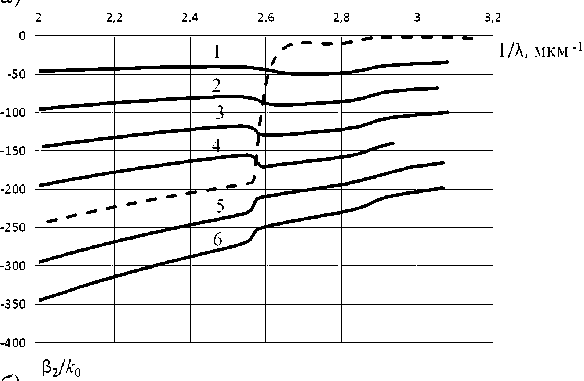
На рис. 7, а приведены дисперсионные характеристики, а на рис. 7, б – характеристики затухания ППВ в диэлектрическом стержне с металлической нанопленкой: а = 5 нм, b = 10 нм, S i = 2.84, S 3 = 1, для нанопленки s _r 0 = 6 (материал серебро), соотношение размеров слоев составляет ( b - a ) / b = 0,5. Внешний радиус структуры выбран равным радиусу сплошного металлического стержня, характеристики ППВ которого приведены на рис. 2, а , б . Характеристики, обозначенные цифрами от 1 до 6, соответствуют

1/Л, мкм

Рис. 7

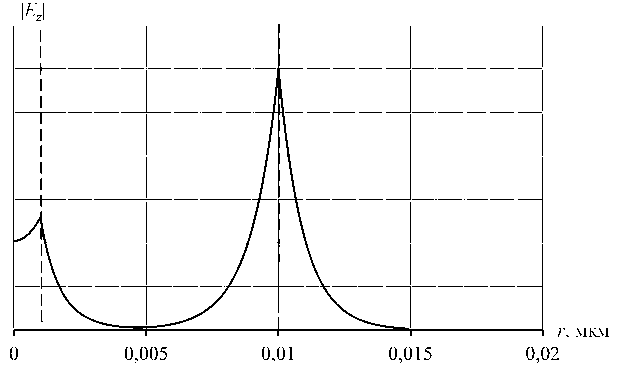
Рис. 10

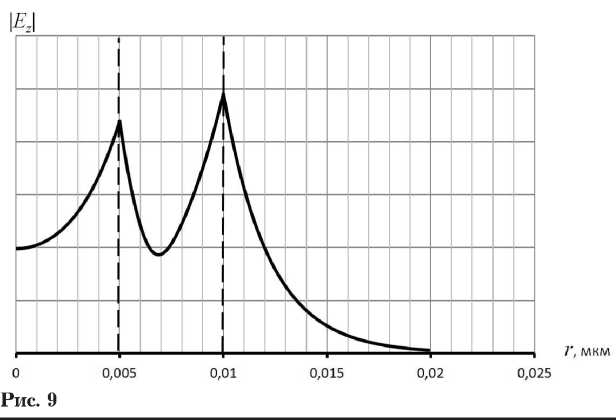
размеров слоев ( b - a ) / b <  0,1 практически сливаются. Затухание волны с индексом 0 уменьшается, а затухание ППВ с индексами 1–6 увеличивается. Характеристики затухания всех ППВ расходятся. Фактически можно говорить о том, что в диэлектрическом волноводе с металлической пленкой очень малой толщины преобладает одна ППВ, имеющая индекс 0. Существованием других волн можно пренебречь в связи с их большим затуханием.

При сравнении характеристик дисперсии и затухания ППВ круглого металлического наностержня (рис. 2) и характеристики ППВ круглого диэлектрического волновода с металлической нанопленкой (рис. 7) можно утверждать, что в металлическом стержне в отличие от диэлектрического волновода с металлической пленкой отсутствует волна с номером – 0, а существуют только волны с номерами 1–6 и выше. Плазмон-поляритонную волну с нулевым индексом можно идентифицировать как «пленочную» (максимумы поля привязаны к краям пленки), а волны с номерами 1, 2, 3 и т. д. как объемные, дополнительные (максимум поля расположены внутри объема электродинамических структур).