Плоское шлифование торцов колец крупногабаритных подшипников с требуемым качеством поверхности

Введение. Крупногабаритные подшипники широко используются в различных отраслях машиностроения и относятся к числу наиболее ответственных узлов механизмов и машин. Основным методом обработки, определяющим геометрическую точность деталей подшипников, является шлифование, поэтому повышение эффективности шлифования колец крупногабаритных подшипников, имеющих высокие требования к качеству поверхности и стоимость изготовления, является актуальной задачей. Как показывает практика, получение требуемой шероховатости торцовой поверхности кольца подшипника возможно без использования выхаживания. Выхаживание применяют для обеспечения допуска плоскостности. Основное время обработки возрастает при этом в среднем на 40 % [1–3].

Обеспечение при шлифовании требуемого допуска плоскостности торцовых поверхностей колец крупногабаритных подшипников, имеющих начальные отклонения от плоскостности и изогнутость торцов в результате термообработки или предшествующих операций механической обработки, является сложной задачей. Наличие отклонений от плоскостности, изогнутости торцовых поверхностей существенно усложняет процесс шлифования, поскольку под действием усилия притяжения магнитного поля стола станка и силы резания кольцо получает осевую упругую деформацию. После шлифования и снятия магнитного поля упругие деформации возвращают определённую величину отклонения от плоскостности обработанному торцу. Различные технологические приемы, использующиеся для устранения отклонений от плоскостно- сти торцов колец подшипников, существенно увеличивают время обработки и стоимость операции [1, 4–8].

При шлифовании колец крупногабаритных подшипников, имеющих начальные отклонения торцовых поверхностей от плоскостности, необходимо учитывать осевые упругие деформации, возникающие от действия усилия притяжения магнитного поля стола и силы резания. Управление величиной осевой упругой деформации позволит уменьшить время и стоимость операции при гарантированном обеспечении геометрической точности детали. Цель исследования – разработка алгоритма и методики выбора оптимальных условий плоского шлифования торцовых поверхностей колец крупногабаритных подшипников из стали ШХ15, обеспечивающих получение заданных требований к качеству обработанной поверхности (параметр шероховатости поверхности R a , допуск плоскостности на операции шлифования ∆ , отсутствие шлифовочных прижогов) при максимальной производительности процесса плоского шлифования.

Методика исследования, математические модели. Математические модели приведённых к ширине образца составляющих силы резания ( p y , p z ), коэффициента шлифования ( К ш ) и шероховатости обработанной поверхности (параметр Ra ) получены методом полного факторного эксперимента типа 2⁴, где 4 – число факторов (табл. 1).

Таблица 1

Математические модели показателей процесса шлифования стали ШХ15

p y ( F 46), Н/мм	p y = 19,9 + 5,45 x 1 + 3,43 x 2 + 0,99 x 3 + 3,67 x 4 + 1,02 x 1 x 2 – 2,40 x 1 x 3 + 2,6 x 1 x 4 + + 0,69 x 2 x 3 – 1,42 x 3 x 4 – 1,49 x 1 x 3 x 4
p y ( F 60), Н/мм	p y = 31,42 + 0,91 x 1 – 3,21 x 2 – 1,02 x 4 + 1,78 x 1 x 2 – 3,44 x 2 x 3 + 0,77 x 3 x 4 + 1,93 x 1 x 2 x 3 x 4 + + 2,06 x 1 x 2 x 3 – 3,078 x 1 x 2 x 4 – 0,73 x 1 x 3 x 4
p z ( F 46), Н/мм	p z = 6,21 + 0,82 x 1 + 0,9 x 2 + 0,82 x 3 + 0,49 x 4 – 0,54 x 1 x 3 + 0,23 x 1 x 4
p z ( F 60), Н/мм	p z = 9,18 + 1,86 x 1 + 0,67 x 3 – 0,27 x 4 + 0,32 x 1 x 3 – 0,38 x 2 x 3 + 0,37 x 3 x 4 + 0,37 x 1 x 2 x 3 x 4 + + 0,72 x 1 x 2 x 3 – 0,35 x 1 x 2 x 4
К ш ( F 46)	К ш = 44,77 – 5,06 x 2 – 13,51 x 3 + 6,15 x 1 x 3
К ш ( F 60)	К ш = 22,75 – 1,97 x 1 – 5,83 x 2 – 1,68 x 3 – 2,61 x 1 x 2 + 1,71 x 1 x 3 – 4,77 x 2 x 3
Ra ( F 46), мкм	Ra = 1,81 – 0,22 x 1 + 0,46 x 3 – 0,22 x 1 x 3
Ra ( F 60), мкм	Ra = 1,92 + 0,27 x 1 + 0,2 x 2 + 0,29 x 1 x 2 + 0,3 x 1 x 3 + 0,26 x 1 x 2 x 3

Экспериментальные исследования проведены при плоском шлифовании периферией круга образцов из стали ШХ15 [9–11]. Для обработки образцов в качестве инструмента использовались электрокорундовые шлифовальные круги прямого профиля со следующими размерами 200× 16×76 четырёх типов: 25AF46К6V, 25AF46L6V, 25AF60К6V, 25AF60L6V. Инструмент изготовлен на ОАО «Волжский абразивный завод».

С учётом производственного опыта были выбраны следующие диапазоны варьирования входных факторов: F – зернистость, меш. (ГОСТ Р 52381) – от F 60 до F 46; с 1 ( х 1 ) – твёрдость шлифовального круга, определяемая звуковым методом по приведённой скорости распространения акустических волн, м/с (ГОСТ Р 52710) – от 4504 м/с ( K ) до 4930 м/с ( L ); t ( х 2 ) – глубина шлифования, мм/ход – от 0,01 до 0,02 мм/ход; v s ( х 3 ) – скорость подачи стола, м/мин – от 10 до 20 м/мин. В скобках дано условное обозначение кодированных значений фактора.

В результате сравнения дисперсий выходных факторов процесса по критерию Кохрена было установлено, что в рассматриваемом диапазоне варьирования дисперсии выходных факторов неоднородны, то есть не выполняется обязательное условие математического моделирования с использованием методики рационального планирования эксперимента. Снижение различия дисперсий достигается уменьшением интервала варьирования факторов. С целью сохранения выбранных интервалов было принято решение о разделении некоторых факторов. Наибольшие дисперсии выходных параметров наблюдаются при шлифовании кругами различной зернистости. Исходя из этого, математические модели выходных параметров процесса шлифования разрабатывали в отдельности для каждой зернистости. Дисперсии составляющих силы резания для кругов одной зернистости в данном случае можно считать однородными.

В результате анализа экспериментальных данных установлено, что в рассмотренном интервале варьирования составляющие силы резания на некоторых режимах шлифования значимо зависят от наработки. В связи с этим в качестве четвертого входного фактора была введена в мате-

Носенко В.А., Тышкевич В.Н., Плоское шлифование торцов колец Орлов С.В., Саразов А.В. крупногабаритных подшипников… матические модели наработка, приведённая к ширине обрабатываемой поверхности, мм2 – V (х4) с интервалом варьирования от 100 до 400 мм2.

Параметр Ra задан в технологическом процессе. Образование шлифовочных прижогов на обработанной поверхности заготовки определяется величиной приведенной к ширине образца касательной составляющей силы резания р z . В результате проведенных исследований установлено, что шлифовочные прижоги появляются при значениях p _z > 6 Н/мм.

Круги зернистостью F 60 и твёрдостью L на всех режимах шлифования не удовлетворяют требованиям производства. Причиной является образование прижогов на обработанной поверхности или нестабильность процесса шлифования. Поэтому для обеспечения требований к качеству обработанной поверхности при оптимизации режимов круги зернистостью F 60 исключены из рассмотрения.

Для разработки математических моделей осевых деформаций кольца под действием усилия притяжения магнитного поля стола станка и радиальной составляющей силы шлифования проведён анализ формы торцовой поверхности наружных колец конического однорядного роликоподшипника из стали ШХ15 (рис. 1, а) с размерами, приведёнными в табл. 2, где: D , D 1 , С – соответственно наружный, внутренний диаметры и ширина кольца; β – угол конусности; r = D 0 /2 – соответственно радиус и диаметр центральной оси кольца, проходящей через центр тяжести поперечного сечения; I zс , I ус и I z , I у – осевые моменты инерции относительно центральных осей z c , у c поперечного сечения кольца и главные центральные моменты инерции (рис. 1, б); α 1 , α 2 – коэффициенты для оценки применимости теории стержней малой кривизны.

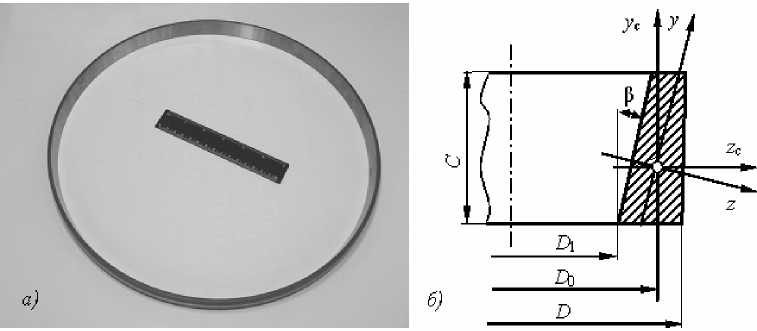
Рис. 1. Исследуемое кольцо ( а ) и поперечное сечение кольца ( б )

Таблица 2

Геометрические параметры исследуемых колец подшипника

Кольцо	D , мм	D 1, мм	C , мм	β, град	r , мм	4 I zc, мм	4 I z, мм	4 I y, мм	α 1	α 2
У-7866A.01	375	357,5	18	15,0	184,2	2939	3001	431	64,3	0,048
1077756.01	460	401	62	12,7	218,4	432 500	439 000	63 610	22,1	0,130

Термообработка колец выполнена в штампах. Исследования проведены на трехкоординатной измерительной машине Millenium . Торцовую поверхность кольца исследовали по окружности среднего диаметра в микропроцессорном режиме. На рис. 2 приведены результаты исследования одного из колец. Отклонение от плоскостности имеет шесть выраженных волн.

Обработка данных показала, что при первоначальном трехопорном контакте поверхностей стола и торца кольца среднее значение углов между точками касания с вероятностью 0,95 составляет 120° ± 16°. Исходя из этого, в расчетной схеме (рис. 3, а) принято, что кольцо касается стола в трех точках, расположенных на равных расстояниях по периметру кольца. Кольцо нагружено сосредоточенной силой Р y (от действия шлифовального круга) и равномерно распределённой нагрузкой q = q _c + q _m (от действия усилия притяжения магнитного поля стола станка q _c и массы кольца q m ), перпендикулярными плоскости кольца.

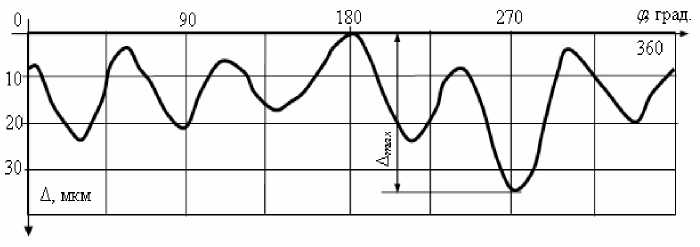
Рис. 2. Форма отклонений от плоскостности торцов кольца после закалки (кольцо конического однорядного роликоподшипника 1077756.01)

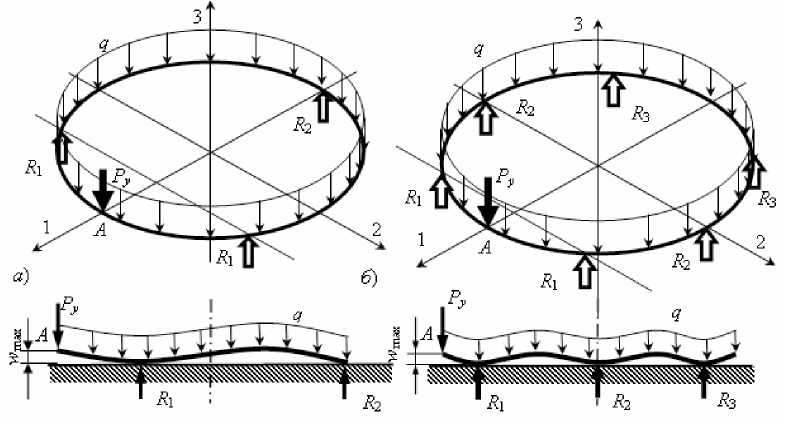
Рис. 3. Расчетные схемы для определения максимальной осевой деформации кольца w max при трёх- ( а ) и шестиопорном ( б ) контакте с поверхностью стола

Трехопорный контакт кольца с поверхностью стола характерен для первоначального момента нагружения. При возрастании нагрузки число опорных контактов кольца с поверхностью стола увеличивается до шести (рис. 3, б).

На рис. 4 показано распределение вершин макроотклонений торцовых поверхностей колец по высоте профиля.

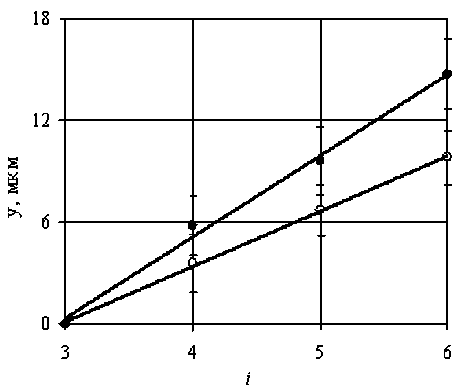
Рис. 4. Распределение вершин макроотклонений по высоте профиля:○ – кольцо 1077756.01;

• – кольцо У-7866А.01

Максимальная осевая деформация при закреплении заготовки кольца магнитным полем стола будет равна:

w _q = w _m + w _qmax + w _qк, где w m , w qmax – максимальная осевая упругая деформация кольца при изгибе, соответственно под действием массы заготовки и усилия притяжения магнитного поля стола; w qк – контактная деформация торцовой поверхности кольца с плоскостью стола.

При шлифовании торца к осевой деформации добавляется максимальная осевая упругая деформация кольца при изгибе w pmax под действием радиальной составляющей силы резания, приложенной в центре пролёта между опорами, и контактная деформация торцовой поверхности кольца с плоскостью стола w pк :

w p = w p _max + w p _к.

Контактную деформацию гладкой поверхности стола и шероховатой волнистой торцовой поверхности заготовки кольца определяли методом Н.Б. Дёмкина. Проведённая оценка величины контактных деформаций позволяет сделать вывод, что её величина для исследуемых колец при наибольших нагрузках не превышает трёх процентов допуска плоскостности. В связи с этим в дальнейших расчетах влияние контактных деформаций не учитывается. Экспериментальные исследования осевых деформаций колец под действием усилия притяжения магнитного поля стола подтверждают это предположение.

Для рассматриваемых колец α 1 = 2π r / C > 10, α 2 = 0,5( D – D 1 )/ r < 0,2 (см. табл. 2). Выполнение данного условия позволяет использовать для определения максимальных осевых упругих деформаций при изгибе кольца w pmax и w qmax теорию стержней малой кривизны. Максимальная осевая упругая деформация кольца при изгибе w pmax и w qmax определяется методом Мора. Статическая неопределимость кольца раскрывается методом сил [5–8].

В общем случае главные центральные оси поперечного сечения кольца z и у могут быть наклонены по отношению к плоскости кольца (см. рис. 1, б). Для облегчения дальнейших вычислений целесообразно ввести вспомогательные коэффициенты: n _y = I ус / I zc ; n z _y = I _y czc / I zc ; П _к = EI у I z / ( GI zc I _к); где I к — момент инерции поперечного сечения кольца при кручении; I _ус, I zc , I у , I _z, I _уczc – осевые и центробежный моменты инерции; E , G – модули нормальной упругости и сдвига материала кольца.

При раскрытии статической неопределимости методом сил разрез кольца располагаем в плоскости симметрии, в точке А (см. рис. 3), что позволяет использовать свойства симметрии и достаточно точно определить один неизвестный изгибающий момент. При действии указанной нагрузки максимальная осевая деформация кольца (прогиб) w возникает в точке А (см. рис. 3) . Используя метод Мора, в полярной системе координат получим:

rI n / / w = ,-, Т ^ Л ПУMzciMzci + ПкМк!Мк! d ^i ,

EIz Iy i=1% L j где Мz/с , Мк/ – изгибающий и крутящий моменты от действия единичной силы; Мzс , Мк – моменты в эквивалентной системе.

Окончательные выражения для максимальной осевой деформации кольца при трёх-, четырёх-, пяти- и шестиопорном контакте торцовой поверхности кольца с поверхностью стола:

wq3 = wqmax3 + wm3 = Ar(63ηy + 7ηк)(qc + qm);(1)

wрmax3 = A(96ηy + 16ηк)Py;(2)

wq4 = wqmax4 + wm4 = Ar(18ηy + 1,1ηк)(qc + qm);(3)

wрmax4 = APy (46ηy + 6ηк);(4)

wq5 = wqmax5 + wm5 = Ar(7ηy + 0,28ηк)(qc + qm);(5)

wрmax5 = APy (26ηy + 3,2ηк);(6)

wq6 = wqmax6 + wm6 = Ar(3,3ηy + 0,1ηк)(qc + qm);(7)

wрmax6 = APy (16ηy + 2ηк);(8)

где A =

r ³ I zc

EI _z I _y 10^{3 .}

С учетом изменения количества опор при закреплении кольца магнитным полем стола станка осевая упругая деформация будет равна:

w q = y i + w qi , (9) где y i – уровень (мкм), соответствующий i -му количеству опор ( y 3 принимаем равным нулю) (см. рис. 4); w qi – осевая деформация при i опорах, 3 ≤ i ≤ 6. Алгоритм вычисления максимальной осевой упругой деформации кольца под действием магнитного поля стола и массы кольца по (9) приведён на рис. 5.

Максимальная осевая упругая деформация при закреплении кольца магнитным полем стола станка и действии радиальной составляющей силы резания c учетом изменения количества опорных контактов будет равна:

w max = y i + w qi + w pi . (10)

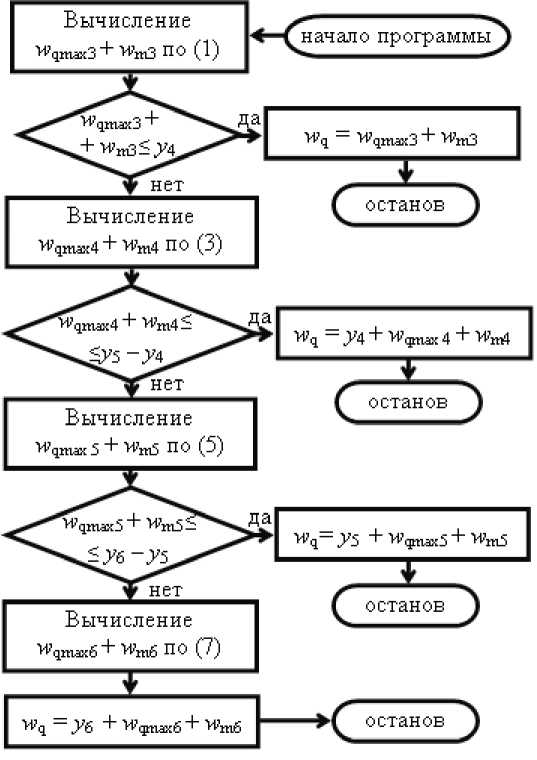
Рис. 5. Алгоритм вычисления максимальной осевой упругой деформации кольца под действием усилия притяжения магнитного поля стола станка и массы кольца

Алгоритм вычисления в этом случае аналогичен алгоритму, показанному на рис. 5 с добавлением деформации w pi .

Для стандартных плит на основе магнитотвердых ферритов (ГОСТ 16528–87) и электромагнитных плит (ГОСТ 30273–98) класса точности А удельная сила притяжения p должна быть не менее 0,16 МПа. Интенсивность равномерно распределенной нагрузки q _c от действия усилия притяжения магнитного поля стола на кольцо будет равна q = pb = 0,16 b , где b = ( D – D 1 ) / 2 – ширина базового торца заготовки кольца (см. рис. 1, б).

Экспериментальная проверка. Экспериментальную проверку теоретических расчетов выполнили при измерении максимальной осевой деформации (максимального прогиба) колец от действия массы заготовки кольца и усилия притяжения магнитного поля стола непосредственно на станке. Кольцо положили на стол станка и произвели его центровку. Магнитную стойку с микронным индикатором закрепили на шпинделе станка и, вращая стол, измеряли отклонение от плоскостности торцовой поверхности кольца. Измерения выполняли через 50 мм по периметру среднего диаметра торцовой поверхности кольца. Затем кольцо закрепляли магнитным полем стола станка и измерения повторяли. В результате измерений определяли величину максимальной осевой деформации. Таким образом, было измерено по 15 колец подшипников 1077756.01 и У-7866А.01.

Относительная погрешность расчетных значений максимальной осевой упругой деформации для кольца 1077756.01 составила 7,6 %, при деформации кольца до пятиопорного контакта торцовой поверхности с поверхностью стола.

Относительная погрешность расчетных значений максимальной осевой упругой деформации для кольца У-7866А.01 составила 14,3 %, при деформации кольца до восьмиопорного контакта торцовой поверхности с поверхностью стола. Для данного кольца осевая деформация продолжалась после шестиопорного контакта по вершинам макроотклонений до следующих контактов по вершинам волнистости.

Полученные экспериментальные данные подтверждают и тот факт, что контактные деформации при закреплении магнитным полем стола практически не влияют на отклонение от плоскостности, поэтому их можно не учитывать в моделях, определяющих условия применимости магнитного поля стола при закреплении заготовки кольца и условия шлифования.

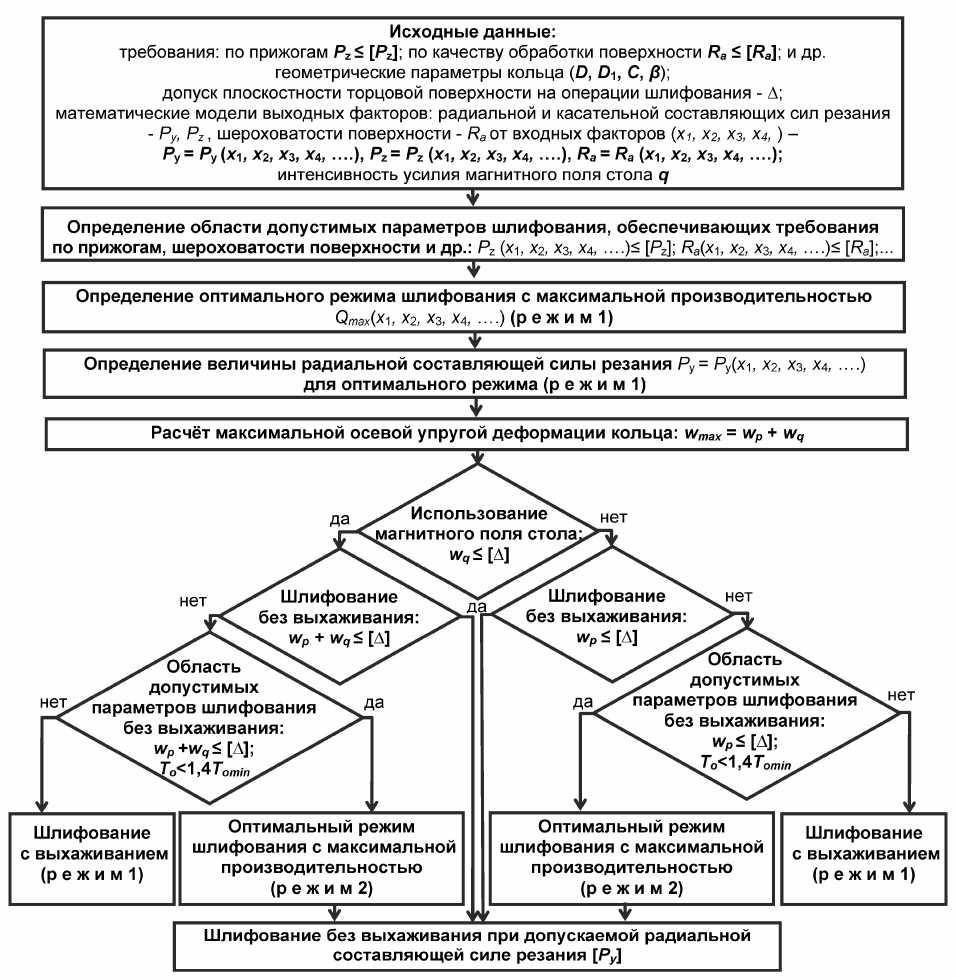
Алгоритм и методика выбора оптимальных условий шлифования. По предлагаемому алгоритму (рис. 6) на первом этапе при выборе оптимальных условий шлифования заготовку кольца рассматривают как абсолютно жёсткую.

Оптимизацию параметров осуществляют из условия выполнения первых двух требований, т. е. обеспечения бесприжоговой обработки и заданного значения Ra . С использованием математических моделей (см. табл. 1) определяют области существования параметров оптимизации, обеспечивающих выполнение требований к данным параметрам качества.

Шлифование без выхаживания S. Wp + Wq < [А]  .

./А/^бласть^ч^ у< допустимых ^Ч^ параметров шлифования без выхаживания:

Область ^ч/^Ч допустимых ^ч параметров шлифования без выхаживания: ^Ч. w_p+w_q< [А];    ./

^ЧТо<1 j 4 Tomiп

/^Использованием^ 1агнитного поля стола.

Исходные данные: требования: по прижогам Pz< [Pz]; по качеству обработки поверхности Ра ^ [Ра]; и др. геометрические параметры кольца (D, Di, С, /3);

допуск плоскостности торцовой поверхности на операции шлифования - А; математические модели выходных факторов: радиальной и касательной составляющих сил резания - Ру, Pz, шероховатости поверхности - Р_а от входных факторов (ху, х₂, х₃, х₄,) -Р_у= P_y(Xi,X₂,X₃,X₄, ....), Pz= Pz (Х_Ъ Х₂, Х₃, Х₄, ....), Ra-Ra (Х_Ь Х₂, Х₃, Х₄, ....);

интенсивность усилия магнитного поля стола q

Определение области допустимых параметров шлифования, обеспечивающих требования по прижогам, шероховатости поверхности и др.: P_z (xi, х₂, х₃, х₄, ■ ■)< [P_z]; R_a(xi, х₂, х₃, х₄, ....)< [Р_а];

Определение оптимального режима шлифования с максимальной производительностью

Qmax^t, Х₂, Хз, Х₄, . . . .) (р 6 Ж И М 1)

нет

....)

нет нет нет

^ Шлифование ^ч. нет без выхаживания: \ w_P5[A] V'C^

Шлифование с выхаживанием (р е ж и м 1)

Оптимальный режим шлифования с максимальной производительностью (р е ж и м 2)

Шлифование без выхаживания при допускаемой радиальной составляющей силе резания [Ру]

Расчёт максимальной осевой упругой деформации кольца: w_max = w_p+ w_q

Определение величины радиальной составляющей силы резания Ру = Py(xi, х2, х3, х4, для оптимального режима (р е ж и м 1)

Рис. 6. Алгоритм выбора оптимальных условий шлифования заготовок колец подшипников с начальными отклонениями от плоскостности торцов

Шлифование с выхаживанием (р е ж и м 1)

Оптимальный режим шлифования с максимальной производительностью (р е ж и м 2)

Оптимальный режим шлифования с максимальной производительностью (р е ж и м 2)

Окончательное выражение целевой функции приведённой производительности Q через варьируемые параметры:

Q = v s ·t· 10³, мм²/мин.

Для круга зернистостью F 46 и твердостью K , решая совместно систему неравенств по р _z и Ra :

р z = 6,21 + 0,82 x 1 + 0,9 x 2 + 0,82 x 3 + 0,49 x 4 – 0,54 x 1 x 3 + 0,23 x 1 x 4 ≤ 6 Н/мм;

Ra = 1,81 – 0,22 x 1 + 0,46 x 3 – 0,22 x 1 x 3 ≤ 2,5 мкм, с подстановкой в них допустимых значений силы и шероховатости для конкретной твердости и зернистости круга определили допустимые значения режимов шлифования (рис. 7).

Область допустимых значений параметров процесса шлифования ниже показанных кривых и левее точек.

Дальнейшая оптимизация параметров в области допустимых значений осуществляется из условия обеспечения максимальной производительности процесса.

Приведённая производительность существенно зависит от твердости круга. Для граничных значений твёрдости К приведённая производительность Q отличается более чем в 2 раза, поэтому целесообразно использовать круги твердости K нижней половины границы твердости.

Коэффициент шлифования возрастает с увеличением твердости (рис. 8) и для данного диапазона составляет около 45.

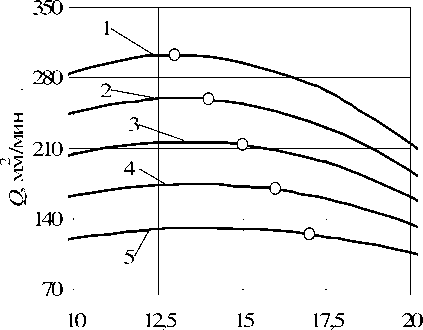
v _s , м/мин

Рис. 7. Приведенная производительность. Зернистость круга – F 46, твердость – K : 1 – 4400 м/с; 2 – 4500 м/с; 3 – 4600 м/с; 4 – 4700 м/с; 5 – 4800 м/с

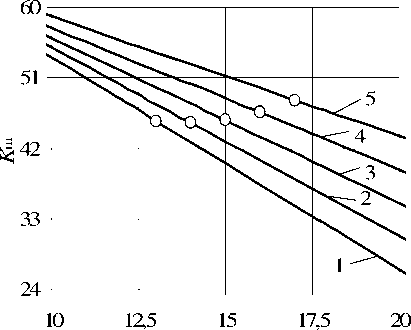
v _s , м/мин

Рис. 8. Коэффициент шлифования. Зернистость круга – F 46, твердость – K : 1 – 4400 м/с; 2 – 4500 м/с;

3 – 4600 м/с; 4 – 4700 м/с; 5 – 4800 м/с

Использовать круги меньшей твердости нельзя, потому что не будет обеспечиваться заданная шероховатость поверхности. Кроме того, существенно увеличивается износ инструмента.

Конкретные режимы шлифования определяются с учетом твердости круга. Для колец из стали ШХ 15 при допустимых значениях [ Ra ] ≤ 2,5 мкм, [ p z ] ≤ 6 Н/мм и для круга 2, находящегося в середине диапазона рекомендуемой твердости оптимальные режимы шлифования (режим 1, см. рис. 6) будут следующими: оптимальная глубина шлифования t _opt = 0,02 мм/ход; оптимальное значение скорости подачи заготовки – v sopt = 13 м/мин; при максимальной производительности Q max = 260 мм²/мин.

Второй этап оптимизации при шлифовании колец подшипников с начальными отклонениями торцовых поверхностей от плоскостности заключается в необходимости учета осевых упругих деформаций при закреплении заготовки. Возможность использования магнитного поля стола станка для закрепления заготовки кольца реализуется при выполнении неравенства:

w q ≤ [ ∆ ], (11) где w q – максимальная осевая упругая деформация при закреплении заготовки кольца магнитным полем стола; допустимая осевая упругая деформация кольца [ ∆ ] определяется формулой:

[∆] = λ∆ – ∆т, где λ – коэффициент запаса точности; ∆ – допуск плоскостности торцовой поверхности на опера- ции шлифования; ∆т – допуск плоскостности при шлифовании жёсткой заготовки, определяемый из справочной литературы.

При невыполнении условия (11) заготовка кольца закрепляется на столе станка упорами.

При закреплении заготовки кольца магнитным полем стола возможность шлифования без выхаживания определена неравенством:

w q + w p ≤ [ ∆ ]. (12)

При шлифовании заготовки кольца без закрепления магнитным полем допустимое значение допуска плоскостности обеспечивается при выполнении неравенства:

w p + w m ≤ [ ∆ ], (13) где w p , w m – максимальная осевая упругая деформация кольца под действием, соответственно, радиальной составляющей силы резания и массы кольца.

Если неравенства (12) и (13) не выполняются, заготовки кольца шлифуют с выхаживанием, что приводит к увеличению основного времени шлифования. В таком случае в области ранее определенных допустимых значений параметров процесса целесообразно найти такие условия шлифования, при которых возможно выполнение следующих условий (см. рис. 6):

w р + w q ≤ [ ∆ ]; T o <1,4 T o min , (14) где T o min – основное время шлифования без выхаживания при максимальной производительности обработки, параметры реализации которой были определены ранее. При существовании области параметров процесса, удовлетворяющих (14), выбор оптимальных условий шлифования осуществляется по критерию максимальной производительности. Полученные параметры процесса определяют оптимальные условия режима 2 (см. рис. 6).

Аналогичный подход реализован при определении оптимальных условий шлифования заготовок колец подшипников, закрепление которых на столе станка осуществляется упорами без использования магнитного поля, он представлен в алгоритме (см. рис. 6).

На основании проведенных исследований разработан способ устранения изогнутости торцов колец шлифованием, при котором шлифование первого торца производится без действия магнитного поля стола с радиальной составляющей силы резания Р у , обеспечивающей осевую деформацию (максимальный прогиб) меньше допуска плоскостности торцов [12].

Для исследуемых колец (см. табл. 2) реализуем второй этап выбора оптимальных условий шлифования. Для определённых на первом этапе из условия обеспечения отсутствия шлифовочных прижогов и параметра шероховатости Ra ≤ 2,5 мкм при максимальной производительности процесса оптимальных режимов шлифования (режим 1) вычисляем величину приведенной силы p y1 :

p y1 = 4,02 + 68· t + 0,278· v s + 27,6· t · v s = 16,2 Н/мм.

Далее рассчитываем деформации w p и w q по математическим моделям (1)–(10) для исследуемых колец. Для исследуемых колец принято λ = 0,75; ∆ = 25 мкм. Для кольца У-7866А.01 – ∆ _т = 7,5 мкм; для кольца 1077756.01 – ∆ _т = 9 мкм.

Для кольца У-7866A.01 проверим условие применимости магнитного поля стола (11). Кольцо под действием усилия притяжения магнитного поля стола опускается до шести опорного контакта с поверхностью стола станка:

w qmax6 + w m6 + y 6 = 12 + 14,8 = 26,8 мкм > [ ∆ ] = 11,3 мкм.

Условие (11) не выполняется. Для закрепления кольца на столе станка необходимо использовать упоры.

Проверяем выполнение условия шлифования без выхаживания (13). Кольцо под действием радиальной составляющей силы резания и массы кольца опускается до шестиопорного контакта с поверхностью стола:

w m6 + w рmax6 + y 6 = 21 + 14,8 = 35,8 мкм > [ ∆ ] = 11,3 мкм.

Условие (13) не выполняется. Для кольца рекомендуется шлифование с выхаживанием при закреплении упорами. Абразивный инструмент – круг 25A F 46 К 6 V при оптимальных режимах шлифования (режим 1) t opt = 0,02 мм/ход; v sopt = 13 м/мин; при максимальной производительности Q max = 260 мм²/мин.

Для кольца 1077756.01 проверим условие применимости магнитного поля стола (1). Кольцо под действием усилия притяжения магнитного поля стола опускается до пятиопорного контакта со столом:

w q = y 5 + w qmax5 + w m5 = 6,7 + 1,2 + 0,03 = 7,93 мкм < [ ∆ ] = 9,7 мкм.

Условие (11) выполняется. Для закрепления кольца на столе станка применимо магнитное поле станка.

Проверяем выполнение условия шлифования без выхаживания (12):

w qmax5 + w m5 + w рmax5 = 1,2 + 0,03 + 1,5 = 2,73 мкм <  y 6 – y 5 = 9,7 – 6,7 = 3 мкм;

w qmax5 + w m5 + w рmax5 + y 5 = 1,2 + 0,03 + 1,5 + 6,7 = 9,43 мкм < [ ∆ ] = 9,7 мкм.

Условие шлифования без выхаживания выполняется. При этом кольцо от действия усилия притяжения магнитного поля стола и радиальной составляющей силы резания опускается до пятиопорного контакта с поверхностью стола.

Кольцо 1077756.01 рекомендуется шлифовать с закреплением магнитным полем стола без выхаживания. Абразивный инструмент – круг 25A F 46 К 6 V при оптимальных режимах шлифования (режим 1) t opt = 0,02 мм/ход; v sopt = 13 м/мин; при максимальной производительности Q max = 260 мм²/мин.

Заключение. Разработанные алгоритм, методика и математические модели позволяют определять оптимальные условия плоского шлифования периферией круга на станке с круглым магнитным столом колец крупногабаритных подшипников из стали ШХ15 с начальными отклонениями торцовых поверхностей от плоскостности. Оптимальные условия обеспечивают получение заданных требований к качеству обработанной поверхности (параметр шероховатости поверхности Ra , допуск плоскостности, отсутствие шлифовочных прижогов) при максимальной производительности процесса плоского шлифования.