Плоское вихревое течение в цилиндрическом слое

С точки зрения моделирования природных явлений и функционирования технических устройств представляют интерес спиральные течения. Такие течения возникают, например, в сливных отверстиях. Различные вопросы, касающиеся экспериментального исследования расходных характеристик и условий формирования воронок при истечении жидкостей, обсуждаются в работах [1–6]. Хорошо известны природные спиральные течения в атмосфере и водоемах Земли, которые реализуются в виде воронок, смерчей и торнадо [7–10]. Подробный обзор подобных исследований приведен в работе [11].

Весьма обширна библиография, отражающая теоретическое изучение, а также математическое моделирование динамики вихревых течений. Теория динамики вращающейся жидкости и ее аспекты применительно к некоторым техническим проблемам изложены в монографиях [12–15]. Анализ различных вариантов постановки краевых условий представлен в [16]. Целый ряд важных результатов получен в [17–30]. Во многих случаях вихревые течения рассматриваются в областях, ограниченных цилиндрическими поверхностями.

В работе [31] рассмотрена задача течения газа через цилиндрическую поверхность во вращающейся системе координат. Показано, что после возникновения радиального течения при стоке газа внутрь цилиндра сразу же начинается формирование спирального течения под действием силы Кориолиса. Решение задачи проводится в рамках модели сжимаемого идеального газа для случая, когда пренебрежение его вязкостью допустимо.

Хорошо известна задача о вращательном течении Тейлора–Куэтта для вязкой жидкости в зазоре между коаксиальными цилиндрами. Начиная с результатов Тейлора [32], которые в дальнейшем получили развитие в работах разных авторов [33–36], установлено, что при превышении угловой скоростью вращения внутреннего цилиндра некоторого критического значения у частиц жидкости «генерируются» поперечные к ранее существовавшим круговым линиям тока составляющие скорости, и в зазоре начинают формироваться вихревые структуры. При этом линии тока у таких структур представляют собой спирали, навитые на торы.

Задача течения между двумя коаксиальными полубесконечными цилиндрами при заглушенном с одного конца зазоре между цилиндрами рассматривалась в [37]. Моделируется асимптотическое течение, которое может формироваться на достаточно большом удалении от свободного торцевого сечения коаксиальных цилиндров. Показано, что в осесимметричном случае структура замкнутых линий тока в зазоре в направлении продольной оси цилиндров приобретает ячеистый характер. При ширине зазора, пренебрежимо малой по сравнению с радиусом внешнего цилиндра, асимптотическое решение получено аналитически.

В работах [38, 39] рассмотрен один класс решений уравнений динамики вязкой жидкости в цилиндрической системе координат для установившегося течения при условии, что радиальная и азимутальная составляющие скорости зависят лишь от радиальной координаты.

К этому же классу относится задача вихревого осесимметричного течения вязкой жидкости в неограниченном пространстве; ее общее решение для радиальной и азимутальной составляющих скорости представлено в работе [40]. Полученное общее решение для азимутальной составляющей скорости содержит две неопределенных константы интегрирования. В [40] приводится частный случай этого общего решения, при этом одна из констант интегрирования априори принимается равной нулю, а вторая константа определяется посредством задаваемой циркуляции потока.

Следует отметить, что общее решение из [40] может быть принято за основу при рассмотрении задачи о плоском течении в цилиндрическом слое при подводе жидкости через внешнюю цилиндрическую поверхность по нормали к ней (радиально) и, соответственно, при вихревом стоке через внутреннюю поверхность. Однако при получении окончательного выражения для распределения азимутальной составляющей скорости здесь возникает необходимость в задании двух граничных условий для определения двух констант интегрирования. В такой постановке задачи, по крайней мере, вид одного из двух необходимых граничных условий для азимутальной составляющей скорости не совсем очевиден.

В данной работе для вихревого осесимметричного течения вязкой жидкости предлагаются варианты записи двух граничных условий для азимутальной составляющей скорости, что позволяет получить точное решение модельной задачи о вихревом стоке, описывающее распределения компонент скорости и давления в цилиндрическом слое при подводе жидкости через внешнюю поверхность по нормали к ней. Проведен также анализ получаемого решения и обсуждаются особенности поля скорости и распределения давления.

• 2.    Постановка задачи

Рассмотрим модельную задачу о плоском установившемся осесимметричном ламинарном течении вязкой несжимаемой жидкости в цилиндрическом слое. Предположим, что жидкость поступает в слой по нормали к его внешней поверхности, имеющей радиус R . На ней поддерживается постоянное давление P . При этом сток жидкости происходит через внутреннюю поверхность радиуса R .

Введем цилиндрическую систему координат традиционным образом. Приняв во внимание следующие допущения: u_z = 0, д/дф = 0 , 5/5 z = 0, запишем уравнения динамики и условие неразрывности потока в безразмерной форме [41]:

, d u ‘   и ;2      1 дP'1

д 2и    1  дии

----L +----LL.

д r 21    r'  д r'r

• и „--^r- --=---- +--

• r дr*   r*     2 дr*Re

• , ди/, ur • u/ _  1  (д2u/ , 1  дu/

Ur7 +-- i— = —7T +—r 77

• дr     r     Re ^ дr r  дrr

1 д( r' • ur )A

.

r'      дr ‘

Здесь- г ' = — uЧ г '1 = ur- _иЧ г '1 =      P ' = 2 P

R ^г ( ) V '        V       р V

л     р VR р VR  р Q штрихом); Re = —— = —2-^2- =--- — число

ц      ц    2пц плотность и динамическая вязкость жидкости;

— безразмерные величины (далее помечаются верхним

Рейнольдса; г — радиальная координата; р , ц — и_г , и^ — радиальная и азимутальная составляющие

скорости потока; P — давление; V , V — известные значения модуля радиальной составляющей скорости на внутренней и внешней цилиндрических границах слоя; Q — абсолютный объемный расход жидкости в расчете на единицу длины вдоль оси O z цилиндрической системы координат.

Для решения системы уравнений (1)-(3) необходимо потребовать выполнения четырех граничных условий. Первые два граничных условия для радиальной составляющей скорости и давления имеют вид- г ' = R2 - и^-V ,   P ' = P2.

Заметим, что (4) представляют собой граничные условия рассматриваемой задачи, но в тривиальном случае чисто радиального течения ( и_ф = 0). Что же касается еще двух граничных условий, необходимых для определения азимутальной составляющей скорости, то они будут предложены ниже.

Характерной особенностью системы (1)–(3) является то, что она допускает определение искомых функций и ’ , и ‘ , P' на основе последовательного решения входящих в нее уравнений в обратном порядке-(3), (2), (1). При этом на первом шаге решение уравнения (3) для радиальной составляющей скорости с учетом граничного условия (4) и очевидного для рассматриваемой задачи соотношения V • R = V • R всегда имеет вид [42] -

1 и.

Г

На следующем шаге после подстановки (5) в (2) придем к дифференциальному уравнению относительно азимутальной составляющей скорости, полученному ранее в [40] и записанному в принятых выше безразмерных обозначениях- d2 и'                1 du'               и'

---^ + (Re +1)- --^ + ( Re -1)-^ = 0 . dг'2 v ’ г' dг' v ’ г2

Общее решение (6) получено в [40], и в безразмерной форме может быть представлено следующим образом-

С. С и ; ⁽ г ) = с + гСь ,

где C , C — неопределенные константы интегрирования.

Отметим, что авторы [40] в рамках общего решения (7) ограничились рассмотрением лишь частного случая, когда считали С₂ = 0. При этом первая константа интегрирования С определялась через задаваемую циркуляцию К и, с учетом безразмерной формы записи (7), равнялась С = К /(2 n R j V ) . Характерной особенностью такого частного случая является то, что в области течения азимутальная составляющая скорости не может в точности равняться нулю.

При конечных размерах области течения в цилиндрическом слое R < г < R определение окончательного вида решения рассматриваемой задачи на основе общего решения (7) при С2 ^ 0 предполагает постановку двух граничных условий для азимутальной составляющей скорости. Приняв во внимание радиальный подвод жидкости в цилиндрический слой через его внешнюю поверхность, одно граничное условие можно получить, потребовав отсутствия такой составляющей скорости на внешней цилиндрической поверхности- г ' = R2 - и ; = 0.

Второе граничное условие для азимутальной составляющей скорости на внешней границе цилиндрического слоя является менее очевидным.

Формально определение азимутальной составляющей скорости из дифференциального уравнения второго порядка (6) в рамках постановки задачи Коши требует удовлетворения еще одному граничному условию для первой производной du ‘ / dr ' . Заметим, что первая производная от азимутальной скорости по радиальной координате непосредственно связана со вторым инвариантом I тензора скоростей деформаций. Тогда на модельном уровне отмеченный выше формализм можно реализовать, задав на внешней границе значение I модуля второго инварианта тензора скоростей деформаций:

Г' = R :      I 2| = 1 2 ь .                                                   (9)

¹ 2       _Г _ ¹ 2 Ь     г J V ]          _{= р р} __р2     _р _ ^du r ^{( r} ) _р . ur ^{( r} )

При этом ¹ 2           ,    1 2 b           ,    ¹ 2 rad Ini ,    ¹ 2^{( r})   ^E rr ^Ефф   ^E r ф ,    ^E rr       ,     ^{, Е} фф

¹ 2 rad             ¹ 2 rad              I ^R 2 J                                             ^{dr                 r}

^E r ф

rd

— ■---

2 dr

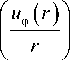
, где

I — значение модуля второго инварианта тензора скоростей деформаций

на внешней границе цилиндрического слоя, определяемое с учетом (5) для случая чисто радиального течения ( и_ф = 0 ), E_r, , Е_ф , Е_гф — компоненты тензора скоростей деформаций.

Принимая во внимание (5) и (8), граничное условие (9) — второе для азимутальной составляющей скорости условие, после некоторых преобразований может быть представлено следующим образом:

r ' = R 2 :

^du ф _{= +}J2_ dr' "R '²

■ 7 ¹ 2 ь - 1.

Варианты выбора знака, заложенные в (10), указывают на возможность реализации двух эквивалентных и противоположных направлений «подкрутки» потока в рамках решения одной и той же исходной системы уравнений. Конкретизация направления течения в ходе его реализации, по-видимому, может определяться особенностями начальной стадии его «запуска» или дополнительными факторами.

Важно, что граничное условие (10) имеет смысл лишь для значений I ‘_ь> 1. Физическая интерпретация постановки граничного условия для азимутальной составляющей скорости в подобном виде в смысле его связи с более традиционными механическими характеристиками будет приведена ниже.

Таким образом, решение рассматриваемой задачи о плоском течении несжимаемой жидкости (о вихревом стоке) при подводе жидкости в цилиндрический слой по нормали к его внешней поверхности должно удовлетворять граничным условиям (4), (8) и (10).

• 3.    Распределения составляющих скорости и давления

Решение задачи для радиальной составляющей скорости имеет хорошо известный, приведенный выше вид (5). Теперь, приняв во внимание граничные условия (8), (10), найдем константы интегрирования в (7) и после соответствующих преобразований получим выражение для определения азимутальной составляющей скорости:

^u ф ^{( r} ') = ±

2 V i k-r 1 ---

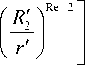
Re - 2   r '

Заметим, что случай, когда второй инвариант тензора скоростей деформаций на внешней границе цилиндрического слоя принимает значение, отвечающее чисто радиальному течению ( I‘_ь = 1), из (11) сразу же приводит к ожидаемому результату: и ‘ ( r ') = 0.

Теперь, подставив (5) и (11) в уравнение (1), после интегрирования с учетом граничного условия (4) найдем выражение для распределения давления:

P'(r') = P2-fl (r') +

( Re - 2 ) 2

4 R 2 ^{Re - 2}

Re

■ f 2 ( r ’)

r>f 2 Re - 4

R ₂

( Re - ¹ )

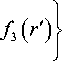
Здесь для краткости записи приняты обозначения:

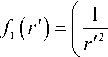
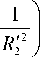
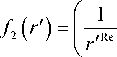
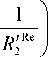
f 3 ( r ') = |-72Re - 2-

_D, 2 Re - 2

R 2

При допущении чисто радиального ( и_ф = 0 ) установившегося течения в цилиндрическом слое R, <  r <  R ₂, когда I'_ь = 1, из (12) для распределения давления вытекает следующий результат:

Pad (Г ') = PP- f (Г') .

При конкретных значениях числа Рейнольдса Re , представляющего собой параметр дифференциального уравнения (6), вид общего решения (7) изменяется. При этом другими становятся и выражения (11) и (12) для распределений азимутальной составляющей скорости и давления. Проведем анализ решения задачи о вихревом стоке для частных значений Re .

Пусть Re = 1. В такой ситуации уравнение (6) упрощается, и его общее решение принимает вид:

с ( 1 )

u'  ( r )=      + С2(1) .

Найдя константы интегрирования C ^{( 1 )} , C ₂ ^{( 1 )} с учетом граничных условий (8), (10), придем к следующему выражению для азимутальной составляющей скорости:

2.I1'-

(1)                   2br

и „ (r ) = ^— ф               r'     L   IR2J

Этот же результат может быть получен при прямой подстановке Re = 1 в решение (11).

Что же касается распределения давления, то для такого частного значения числа Re оно после подстановки (5), (14) в (1) и решения последнего с учетом граничного условия (4) определяется следующим образом:

P '™( r ■)=P-f. (r')+4 (I: b -i)-|-f (r ')+-4-f 1 - -41+-2- - ь f r- 'll.

[       R ^ r R J R2   (R J J

Если в (12) выполнить предельный переход при Re ^1 и раскрыть возникшую при этом неопределенность по правилу Лопиталя, то придем в точности к выражению (15):

lim{P'(r')} = P'(1)(r') .

Re ^ 1 ⁴

По аналогии рассмотрим другой частный случай, когда Re = 2. Подставив это значение в (6), получим несколько иной вид дифференциального уравнения, общее решение которого для азимутальной составляющей скорости тоже выглядит по-другому:

u

' ( 2 ) =

ф

C ^{( 2 )} r'

C ₂ ^{( 2 )}- ln( r '1 r'

где C j^{( 2 )} , C ₂ ^{( 2)} — константы интегрирования, соответствующие значению Re = 2.

Удовлетворив граничные условия (8), (10), получим следующее выражение для распределения азимутальной составляющей скорости:

и ,⁽ 2 ) = _± з^^Й! . in ^f    ) .                                     (16)

ф           r'        (R' J

Подстановка (5) и (16) в (1) и учет граничного условия (4) дают распределение давления для рассматриваемого числа Re :

P,(2)(r‘) = PM1 + 2(12b-1))-f1 (r‘) —

4 ( 1 2 b - 1 )

r '2

1 + In

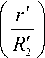
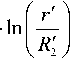
Переход в (11) и (12) к пределу при Re — 2 и раскрытие возникших при этом неопределенностей в точности приводят к только что найденным выражениям (16) и (17):

lim { u ; ( r ' ) } = u ; ^{( 2 )} ( r ' ) . lim { P'(r ' ) } = P "²⁾ ( r • ) . Re — — 2                                  Re — — 2

Иначе говоря, решения, отвечающие значениям Re = 1 и Re = 2 содержатся в решениях (11) и (12). Это обусловлено тем, что вид (6) для задачи о вихревом стоке удовлетворяет теореме о непрерывной зависимости решения дифференциального уравнения от параметра; здесь его роль играет число Рейнольдса.

• 4.    Анализ и некоторые особенности установившегося плоского спирального течения

Прежде всего, отметим следующее: проанализировав соотношения (5) и (11), можно увидеть, что по мере приближения рассматриваемой в области течения точки к внутренней границе цилиндрического слоя азимутальная составляющая скорости существенно растет. В качестве примера на рисунке 1 показан характер изменения модуля отношения азимутальной и радиальной составляющих скорости в зависимости от радиальной координаты при различных значениях числа Рейнольдса:

yU (r ') =

u ф^{( r} ' ) u r ( r ' )

2 V i 2r- T —

Re - 2

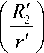
Влияние параметра R2 на величину соотношения (18) в зависимости от числа Рейнольдса на выходе из цилиндрического слоя при r' = 1 демонстрируют графики, изображенные на рисунке 2.

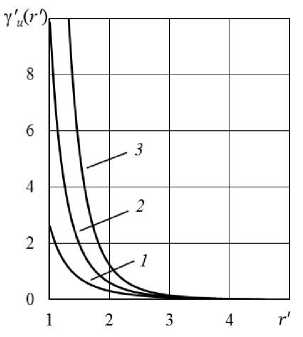
Рис. 1. Изменение соотношения между азимутальной и радиальной составляющими скорости в зависимости от радиальной координаты при   I ‘_ь = 1,001;   R ‘ = 5

и различных значениях Re : 5 (кривая 1 ); 6 ( 2 ); 7 ( 3 )

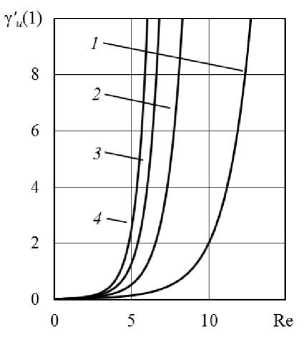
Рис. 2. Изменение соотношения между азимутальной и радиальной составляющими скорости на выходе из цилиндрического слоя в зависимости от Re при I‘_ь = 1,001 и различных значениях R : 2 (кривая 1 ); 3 ( 2 ); 4 ( 3 ); 5 ( 4 )

По представленным на рисунках 1 и 2 кривым видно, что азимутальная составляющая скорости в непосредственной окрестности выхода из цилиндрического слоя начинает доминировать над радиальной составляющей. При этом для исследованных наборов числовых значений исходных параметров азимутальная составляющая скорости на выходе из цилиндрического слоя может превышать радиальную составляющую на порядок и более.

Заметим, что именно такой характер соответствия между составляющими скорости, по крайней мере, на качественном уровне, имеет место для реальных природных вихревых течений в атмосфере типа смерчей и торнадо. Для сравнения скажем, что известное из [40] решение вида (7) при С₂ = 0 предсказывает всюду в области течения одну и ту же величину соотношения азимутальной и радиальной составляющих скорости, а именно:

YU (r ') =

u 2 r') ur (r')

K

= const.

Q

Рассмотрим некоторые особенности семейства линий тока для полученного распределения компонент вектора скорости (5), (11) в задаче о вихревом стоке в случае установившегося плоского спирального течения. В полярной системе координат уравнение для определения линий тока записывается следующим образом:

dФ _ 1 u2r') dr'    r' и’ (r')

Граничное условие для этого уравнения может быть задано как

r ' = R :    ф = фо,

где ф0 — угол, определяющий положение начальной точки на внешней границе цилиндрического слоя для построения линии тока, проходящей через эту точку.

Приняв во внимание (5) и (11), с учетом граничного условия (20) придем к решению уравнения (19) вида:

ф(r') = Фо ±

2/ 1 —1 (Re - 2) 2

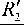
I r' )

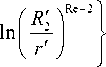
Отличительной особенностью поля скоростей рассматриваемого установившегося течения является то, что линии тока, удовлетворяющие решению (21), имеют форму спиралей, которые допускают наличие точки перегиба. Попутно отметим, что большинство известных плоских спиральных кривых (спирали Архимеда, Фибоначчи, логарифмическая, гиперболическая и другие) не имеют точки перегиба. В ряду немногих аналогов можно выделить, пожалуй, лишь так называемую спираль Римского жезла (спираль Lituus), каждая из двух ветвей которой также имеет точку перегиба.

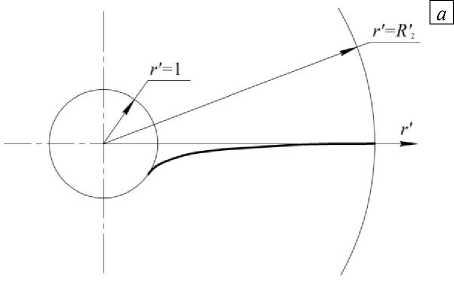
R inf <  1 ( а ) и для Re = 7 , R f = 1,813 ( б )

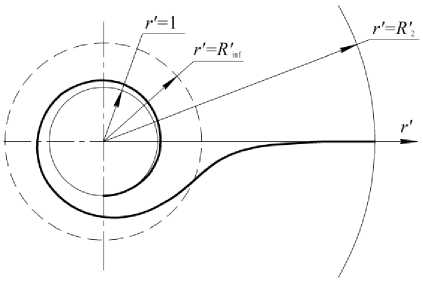
Рис. 3. Линия тока для установившегося течения в цилиндрическом слое при I ‘₆ = 1,001, R = 5 , ф₀ = 0 для Re = 4,25 ,

Типичные примеры двух различных вариантов линий тока, построенных в соответствии с (21) для сравнительно малого и достаточно большого значений числа Рейнольдса, изображены на рисунке 3. Основное отличие представленных здесь двух видов линий тока заключается в следующем. При сравнительно небольших значениях числа Рейнольдса линия тока не имеет точки перегиба в диапазоне изменения радиальной координаты 1 <  r ' <  R ‘ (Рис. 3 а ). В случае же достаточно больших значений числа Рейнольдса линия тока принимает такую форму, у которой появляется точка перегиба при некотором значении радиальной координаты r ' = R е [ 1; R ‘ ] (Рис. 3 б ).

Условие существования точки перегиба на произвольной линии в полярной системе координат задается следующим дифференциальным соотношением:

d ²ф dr ’ ²

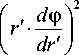
^ = о dr*

После подстановки (21) в (22) придем к уравнению для определения радиуса r ' = R ‘_f окружности, на которой в рассматриваемом спиральном течении располагаются точки перегиба семейства линий тока. Уравнение решалось численно, методом секущих. Представление о характере зависимости от числа Рейнольдса корня этого уравнения, определяющего, с учетом (21), положение точки перегиба на линии тока, дают графики, изображенные на рисунке 4.

В диапазоне значений радиальной координаты R ‘ ^ <  r' <  R линия тока монотонно удаляется от радиальной оси. После же прохождения точки перегиба в диапазоне 1 <  r' <  R ‘_f линия тока отклоняется в другую сторону и начинает закручиваться вокруг оси симметрии вплоть до выхода через внутреннюю границу цилиндрического слоя.

На рисунке 5 приведены распределения давления в малой окрестности выхода из цилиндрического слоя при I 2₆ = 1,01 и Р ₂' = 50, вычисленные по формуле (12) и отнесенные к соответствующим распределениям давления (13) в случае чисто радиального течения ( I‘_ь = 1):

Yp (И" P'(r'VPa (rЪ

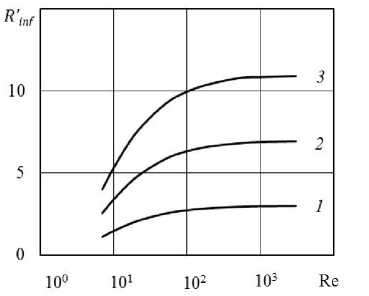
Рис. 4. Влияние величины числа Рейнольдса на положение точки перегиба линии тока при I’_ь = 1,001 и различных значениях R’ : 3 (кривая 1 ); 7 ( 2 ); 11 ( 3 )

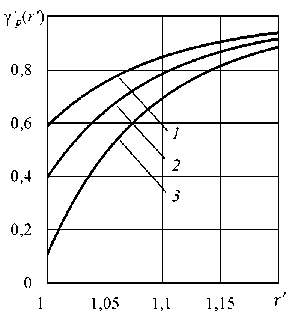
Рис. 5. Зависимость соотношения (23) от радиальной координаты при R = 3,6 и различных значениях числа Рейнольдса Re : 6,2 (кривая 1 ); 6,4 ( 2 ); 6,6 ( 3 )

Из анализа зависимостей, изображенных на рисунке 5, следует, что в плоском спиральном течении давление в достаточно малой окрестности выхода из цилиндрического слоя принимает более низкие значения по сравнению с аналогичным давлением в чисто радиальном течении.

Приняв во внимание отмеченную выше особенность распределения давления в плоском спиральном течении в окрестности выхода из цилиндрического слоя и выполнение условия P ' ( 1 ) <  P_d ( 1 ) , сделаем следующее предположение: возможно, возникновение природного эффекта торнадо есть следствие снижения (его причины здесь не обсуждаются) давления на границе «стока» (на условных границах центрального «ствола» торнадо) ниже уровня, соответствующего давлению при чисто радиальной схеме течения.

• 5.    Альтернативный вариант записи второго граничного условия

для азимутальной составляющей скорости

Следует отметить, что постановка граничного условия в форме (9) для второго инварианта тензора скоростей деформаций не является традиционной. Это обусловлено тем, что характеристика I , вообще говоря, не совсем удобна с точки зрения ее непосредственного экспериментального определения и последующего использования. В этой связи рассмотрим другой по форме, но эквивалентный по своей сути вариант записи второго граничного условия, которое по совокупности с граничным условием (8) позволило бы полностью определить константы интегрирования C , C в (7).

Как следует из поведения функции (23), отличительная черта плоского спирального течения заключается в том, что давление P' (1) = P ' на выходе из цилиндрического слоя принимает значения меньшие, нежели значения, получаемые при прочих равных параметрах в задаче чисто радиального течения. При этом давление P', определяемое из (12) на выходе из цилиндрического слоя, по существу, определяется посредством задания на входе в слой значения I^. Иначе говоря, между этими величинами имеет место взаимно однозначное соответствие. В этой связи вместо граничного условия (10) для производной функции и‘ по радиальной координате на входе в цилиндрический слой предлагается принять для давления, но на выходе из цилиндрического слоя, следующее условие:

r ‘ = 1:    P ' = P1.

Здесь, естественно, предполагается, что P ' является заданной величиной, которая удовлетворяет условию P '< P ^ ( 1 ) . Отметим также, что (24) в данном случае представляет уже, наряду с (4), второе граничное условие для давления, несмотря на то, что дифференциальное уравнение (1) относительно функции P ( r ) имеет только первый порядок.

Тогда, с учетом нового граничного условия (24), решение задачи об установившемся плоском спиральном течении в цилиндрическом слое должно проводиться в следующей последовательности: – выражение для радиальной составляющей скорости по-прежнему определяется соотношением (5), поскольку вытекает из условия неразрывности;

– с учетом граничного условия (8) выражение (7) для азимутальной составляющей скорости потока может быть преобразовано к виду:

u;(r ,)=r. •

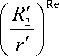
– подстановка (5) и (25) в (1) и последующее интегрирование с учетом граничного условия (4) приводит к следующему выражению для распределения давления:

P‘(r') = P2-f1 (r') + С •bfl (r') +

4 • R ^,R 2

Re

• f2 (Г')

-

_Dr 2 Re - 4

^R 2

( ^Re - 1 )

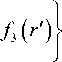
которое структурно, как и следовало ожидать, совпадает с (12);

– в соответствии с граничным условием (24) из (26) следует формула для определения последней неизвестной константы:

( P 2 - P I — f i ( 1 ) ) ' Re - ( Re - 1 )

C = ±

• f 2 ( 1 ) + Re ' R 2 ^{Re - 4} • f з ( 1 ) .

¹ RReR Re - 1 ) . f. ( 1 ) - 4 ( Re - 1 ) ' R 2 ^{Re - 2}

Таким образом, несмотря на альтернативный вариант второго граничного условия в виде (24), для определения азимутальной составляющей скорости он оказывается эквивалентным граничному условию вида (9). Это обусловлено, как уже отмечалось выше, тем, что между значениями I ‘₆ и P ' имеет место взаимно однозначное соответствие.

В силу последнего утверждения из условия P '< P ^ ( 1 ) непосредственно вытекает результат: I ‘₆ >  1, при котором имеет смысл граничное условие (10). Действительно, приняв во внимание (5), (25) с учетом граничного условия (8) сразу же получим:

, , C ² (Re - 2) 2 1 1 2 ( R 2 )|= 1 2 b = 1 + ^{1 (}₄ ) >  1.