Почти достоверная модальная логика шкал Крипке с функциональным отношением

В современной математике активно изучаются случайные структуры, такие как случайные отношения на заданном множестве. Одним из основных способов изучения случайных структур является их описание с помощью логических языков.

Достаточно хорошо изучено описание случайных отношений на языке первого порядка. Широко известен закон нуля или единицы для случайных отношений, утверждающий, что любое определимое на языке первого порядка свойство случайного отношения на п- элементном множестве имеет асимптотическую вероятность, равную нулю или единице. Этот закон доказали независимо Глебский, Коган, Легонький и Таланов [1], и Фейгин [2]. В последней работе описывается аксиоматизация для множества всех предложений, которые верны для случайного отношения с вероятностью, стремящейся к единице, или асимптотически почти наверное.

Представляет интерес характеризация случайных отношений на языках неклассических логик. Бинарные отношения можно описывать на языке модальной логики с помощью семантики Крипке. Случайные шкалы Крипке и случайные модели Крипке демонстрируют различное поведение: в частности, для моделей Крипке выполнен закон нуля и единицы [3], в то время как для шкал Крипке он нарушается [4]. В этой статье мы ограничимся рассмотрением случайных шкал Крипке.

(с) Слюсарев В. В., 2024

@ Федеральное государственное автономное образовательное учреждение высшего образования «Московский физико-технический институт (пациопальпый исследовательский университет)», 2024

Множество формул, которые выполнены асимптотически почти наверное в данном семействе случайных шкал Крипке, назовём почти достоверной логикой этого семейства. Горанко [5] описал почти достоверную логику случайной счётной шкалы Крипке и показал [6], что она содержится в почти достоверной логике конечных шкал Крипке. Задача полной аксиоматизации почти достоверной логики конечных шкал Крипке остаётся открытой; согласно Горанко [6], она может быть не конечно аксиоматизируемой и даже не перечислимой. Задача аксиоматизации почти достоверной логики, однако, может быть более выполнимой для более узких классов шкал Крипке, среди которых наибольший интерес представляют классы шкал, определяемые нормальными модальными логиками. Вербрюгге [7] доказала закон нуля и единицы для случайных конечных шкал модальной логики GL и аксиоматизацию для почти достоверной логики этого класса. Из этого результата следует, что почти достоверная логика конечных GL-шкал является строгим нормальным расширением логики GL.

В этой статье мы рассматриваем почти достоверную логику класса шкал модальной логики SL. Известно, что логика SL определяет класс шкал Крипке, в которых отношение является функцией. Классический результат Сегерберга [8] служит примером простой структуры, характеризующей эту логику: SL полна относительно шкалы на множестве натуральных чисел с отношением следования. В общем случае шкалы, в которых общезначима логика SL, устроены гораздо более нетривиально.

В разделе 1 вводятся основные термины и обозначения и формулируются классические утверждения теории моделей модальной логики, которые используются для решения поставленной задачи. В разделе 2 формулируется и доказывается теорема 1 о включении почти достоверной логики класса шкал, заданного некоторой модальной логикой, в почти достоверную логику класса связных шкал этой логики. В разделе 3 описывается комбинаторная структура связных конечных шкал логики SL и доказывается, что SL является почти достоверной логикой связных конечных SL-шкал. По теореме 1 из этого следует основной результат: SL также совпадает с почти достоверной логикой всех конечных SL-шкал.

1.1.    Модальная логика

Определение 1.  [9] Зафиксируем счётное множество пропозициональных перемен ных PV := {р1, р2, ...}. Определим множество ML модальных формул как множество всех строк р в алфавите PV U {(, ), —, V, О}, удовлетворяющих БНФ-выражению:

р ::= 1 | pi | (р ■ г< | Пр,       i G N.

Введём сокращение: Ор := —□—р.

Определение 2. [9] Множество формул L назовём нормальной модальной логикой, если:

• 1)    L содержит все тавтологии классической логики;

• 2)    L содержит аксиому нормальности П(р1 ^ р₂) ^ (Пр1 ^ Пр₂ У,

• 3)    L замкнуто относительно правил вывода:

(МР) если р G L , р ^ ф G L , то ф G L для любых р, ф G ML:

(Gen) если р G L, то Пр G L для любой р G L;

(Sub) если р G L, то р[ф/р] G L, где р G PV, р,ф G ML, р[ф/р] —результат замены всех вхождений переменной р в формуле р на формулу ф.

Определение 3. Пусть SL — минимальная нормальная модальная логика, содержащая формулы Пр ^ Ор 11 Ор ^ Пр.

1.2.    Шкалы Крипке

Определение 4. [9] Шкалой Крипке называется пара F = (X,R), где X = 0 — множество. R С X х X — отношение. Множество X в этом случае бе дем обозначать dom F.

Обозначение. Пусть F = (X, R) — шкала Крипке. Обозначим:

• 1)    R 0 = {(_а, а) | a G X} ;

• 2)    R - 1 = {(a,b) | a, b G X, bRa} ;

• 3)    R^{n +} := {(a, b) | Зс G X (aRc и cRⁿb)} для всех п ф 0;

• 4)    R* = Ujto R *; —рефлексивно-транзитивное замыкание R;

■ф R(a) := {b G X | aRb} для лтобого a G X.

• 6)    R(U ) := UaebR(a) Для любого U С X.

• 7)    R \U :=R П (U xU ) для любого U С X.

• S)    F \U :=(U,R \ U) для любого U С X.

Определение 5.   [9] Оценкой в шкале Крипке F = (X,R) называется функ- пня V : PV Ф 2х. П;;фа (F,V) в этом случае называется моделью Крипке. Тройка (F,V,x), где x G X, называется отмеченной моделью Крипке.

Определение 6. Пусть F = (X,R), G = (Y,S ) —шкалы Крипке. Биекция f : X Ф Y называется:

• 1)    изоморфизмом шкал F и G, если для любых a, b G X верно aRb ФФ f (a)Sf (b);

• 2)    изоморфизмом моделей (F, V ) и G, U, где V : PV Ф 2^х и U : PV Ф 2^y, если выполнено условие 1 и для любых a G X, р G PV выполнено a G V(р) ФФ f (a) G U(p);

• 3)    изоморфизмом отмеченных моделей (F,V,x) и (G,U,y) где V : PV Ф 2^х, x G X, U : PV Ф 2^y, у GY, если выполнено условно 2 ii f (x) = y.

Две шкалы Крипке (модели Крипке, отмеченные модели Крипке) называются изоморфными, если между ними существует изоморфизм. Отношение изоморфности обозначается символом = .

Определение 7. [9] Пусть (F, V, x) — отмеченная модель Крипке, F = (X, R), р G ML . Отношение F, V, x = р фр истиина в (F, V, x)} определяется индуктивно:

• 1)    F, V, x = Т

• 2)    F, V, x |= р ФФ x G V (р). г;те р G PV:

• 3)    F, V, x |= (р Ф ф), если F, V, x 1= р или F, V, x |= ф, где р, ф G ML;

• 4)    F, V, x |= Пр, сс. th Vy G R(x) (F, V, у |= р). где р G ML .

Предложение 1. [10] Пусть р G ML . Если отмеченные модели Крипке (F, V, x) и (G, U, у) изоморфны, то F,V,x |= р ФФ G,U,y |= р.

Определение 8. Формула р общезначима в шкале Крипке F = (X,R), если для любой опенки V : PV Ф 2^х н любой x G X выполнено F, V, x |= р.

Предложение 2.  [10] Пусть р G ML. Если шкалы Крипке F и G изоморфны, то F |= р фф G |= р.

Определение 9. Логикой Log Л класса шкал Крипке Л называется множество всех формул 9? G ML , таких что F = р для любой F G Л .

Определение 10. Классом шкал ЕтГ множества формул Г С ML называется класс всех шкал F, таких что F = р для любой р G Г.

Замечание. Если Л = {F} ил и Г = {?}, то фигурные скобки могут опускатвся, например: F |= Г; LogF; Frp.

Определение 11. Рекурсивно определим функцию md : ML м N —модальную глубину формулы:

• 1)    md(±) = 0;

• 2)    md(p) = 0 для л тобой р G PV ;

• 3)    md(p м^) = rnas{md(?), md(^)};

• 4)    md(Q?) = md(p) + 1.

Определение 12. Пусть F = (X, R) —шкала Крипке, V —оценка, ж G X. Пусть п G N.

Определим усечённую отмеченную модель Мф^п = (Тф", V^ⁿ, ж), где

п

X = JW); R = ^R rxfⁿ; F = X ,R ■ ; V<ⁿ(p) = V(р)ПХ ^ⁿ(x), р G PV.

i=0

Лемма 1. Пусть F = (X,R) —шкала Крипке, V —оценка, x G X. Пусть п G N. Тогда для любой формулы ?, md(p) <  п, верно

F,V,x = ? ^ F<™V^,x|=p.

Данная лемма является частным случаем леммы об п-бисимуляции [10, Лемма 31].

1.3.    Случайные шкалы и почти достоверные логики

Определение 13. Пусть [п] = {1, ..., п}. Обозначим Л _п множество всех шкал Крипке вида, ([п], R) , где R С [п] х [п].

Определение 14. Пусть Л —непустой класс шкал. Для любого п G N определим случайную шкалу Л_п(Л ) как случайный элемент со значениями в Л П Л_п с равномерным распределением:

P(Fn (Л) G A) = ^|ЛП^2^ , ГДО А С Лп ПЛ. ^|Л п ^{п Л} |

Замечание. Изоморфные шкалы считаются различными.

Определение 15. Почти достоверной логикой Logas(Л) класса шкал Л называется множество формул р G ML. таких что lim P(Fn(Л) = р) = 1.

п^ж

Предложение 3. Для любого класса шкал Л , Log Л С Log^as(Л).

Доказательство. Пусть р G Log Л, тог да Л С Frp. По (1), для любого п G N,

Р(Й(Л) =?) = £^1 |Л П Л n |

| ЛПЛ п | ₌ 1

| ЛПЛ п |    ’

так что р G Log ^as (Fr L ).   □

Обозначение. Если L —нормальная модальная логика, то обозначим F_n( L ) := F_n(Fr L ) и Las :=Log ^as (Fr L ).

В этой работе мы исследуем логику SL^as .

2. Логики случайных связных шкал

Определение 16. Пусть F = (X,R) — шкала Крипке. Определим отношение

• <^ := (R U R^-1)*.

Предложение 4. Для любой шкалы Крипке F = (X,R) ^^ - отношение эквивалентности на множестве X.

F

Определение 17. Классы эквивалентности по отношению ^^ назовем компонентами связности шкалы F. Шкала Крипке F называется связной, если она содержит ровно одну компоненту связности.

Обозначение. Если F — класс шкал Крипке, то ConF — класс всех связных шкал в F.

Для многих модальных логик L задачу определения почти достоверной логики L as можно свести к задаче описания почти достоверной логики Log^as(ConFr L ) связных шкал логики L .

Определение 18. Пусть F = {(Xj,Rj)}j_£j — множество шкал Крипке, где I — некоторое непустое множество. Несвязной суммой |+J F множества шкал F называется шкала (X,R), где

X = {(i,a) | a G X i , г G I }; {i,a)R{j,b) ^^ i = j, aR_ib.

Обозначение. Обозначим F₁ W F₂ := [+l_ie{_{1 2}} F_i.

Лемма 2. [10] Пусть I —непустое множество, {Fi = (X_i, R_i)}_iei —набор шкал Крипке, F = 1Д_е/ Fi. Toгда Log F = Q_ieJLog Fi.

Определение 19. Пусть F G Fn, n G N. Положим m := max {|C| | C G [n] J J^ } ;

k := min {k G [n] | 3C G ^[n] J J^ : k G C, |C | = m} .

Пусть C — компонента связности F. содержащая точку k. Обозначим MC(F ) = F \ C.

Замечание. MC(F ) — сужение F на компоненту связности, которая содержит точку с минимальным номером среди всех компонент максимального размера. В частности, MC(F ) — связная шкала Крипке, и | domMC (F )| ^ |C| для любой C G ^[n] J J^ .

Предложение 5. Для любой шкалы Крипке F G F_n, LogF С Log MC (F ).

Доказательство. Заметим, что F = MC(F )W F \ ([n]\domMC (F )). Утверждение следует из леммы 2.   □

Определение 20. Пусть U С N — конечное множество. Обозначим F y множество всех шкал Крипке вида (U, R), R С U х U.

Предложение 6. Пусть L — модальная логика, n G N, U С [п]. При условии domMC (F_n ( L )) = U, случайная шкала MC(F_n(Ly) равномерно распределена на F y О Con Fr L :

P(MC(F_n( L )) = G 1 | domMC(F_n( L )) = U) = P(MC(F_n( L )) = G 2 | domMC(F_n( L )) = U )

для любых G₁, G₂ G F y П ConFr L , г,те P(A | B) := Ppygy)

— условная вероятность.

Доказательство. Зафиксируем п G N, подмножество U С [п] и шкалы Gi = (U, Si), G 2 = (U,S2) G F u n ConFr L. Так как domGi = domG2 = U, по определению условной вероятности достаточно показать, что

P(MC (F„(L)) = G1) = P(MC (F„(L)) = G2), что в силу (1) эквивалентно

|{F G F_n П Fr L : MC(F ) = Gi}| = |{F G F_n П Fr L : MC(F ) = G2}| .

Построим биекцию f между этими двумя множествами. Пусть F = ([n],R) G Fn П Fr L такова, что MC(F) = Gi. Определим шкалу f (F) = ([n],R‘), где aRb FF I

aRb, если a, b G U ;

• a, b G [п].

aS ₂ b, если a, b GU,

Заметим, что F = G 1 l±l F \ ([п] \ U ), так что по лемме 2 L С LogF [ ([п] \ U ). Далее, f(F ) = G2 OF [ ([п] \U ) 11. поскольку G 2 |= L,

Log f (F ) = Log G2 П Log F \ ([п] \U ) D L.

Таким образом, f (F ) G F_n П Fr L.

По условию domGi = U является компонентой связности в F. По построению отношения R, между U и [п] \ U не существует R’-стрелок, так что U также является компонентой связности в F ‘. Так как при этом R' совпадает с R и а. [п] \ U, полученная шкала f (F ) имеет то же множество компонент связности, что и F. Следовательно, dom MF (f (F )) = U. Поскольку f (F ) [ U = G 2 , имеем MT(f (F )) = G 2 , как и требовалось.

Для любой шкалы F = ([n],R‘) G Fn П Fr L, удовлетворяющей MC(F) = G2, справедливо f-1(F) = ([п], R), где aRb FF I

aR'b, если a, b GU ;

• a, b G [п].

aS 1 b, если a, b G U,

Следовательно, f является биекцией между множествами {F G F_n П Fr L : MC(F ) = Gi} и {F G F_n П Fr L : MC(F ) = G2}, так что их мощности равны. □

Предложение 7. Пусть L — модальная логика, п G N, U С [п], |U| = т. Тогда для любой модальной формулы ^:

P(MC (F_n (L)) = р | domMC (F_n( L ) = U) = P(.F_m(ConFrL) = ^).

Доказательство. Множество U равно мощно [т], так что существует биекция f : [т] ^ U. Определим биекцию f между множествами F u П ConFr L и F [ _m ] П ConFr L : для любой шкалы F = (U, R) G F u П Con Fr L ПОЛОЖИМ

f(F ) = ([m],R‘), aRb FF f(a)Rf(b), a,b G [т].

Заметим, что f является изоморфизмом между F 11 f (F ). Тогда для любой F G F u П ConFrL и любой модальной формулы ^ имеет место эквивалентность:

^F = ^ ^{FF f ( F} ) = F

По предложению 6, при условии domMC(F„(L) = U ) случайная шкала MC (F„(L)) равномерно распределена на F u П ConFr L, следовательно, f (MC (F„(L))) равномерно распределена на F_n П ConFrL при этом же условии. Тогда утверждение следует из равномерного распределения /’„(ConFrL) нa F_n П ConFrL.   □

Определение 21. Пусть п G N. Числом Белла В_п называется число разбиений множества [л] на непересекающиеся подмножества.

Определение 22. Пусть п, г G N. Обозначим G_n , _r число всех разбиений множество [п] на непересекающиеся подмножества, каждое из которых имеет мощность не более г.

Предложение 8. Для любых г, к G N выполнено асимптотическое соотношение:

G_n , _r2^пк = о(В п ), п мот.

Доказательство. Известны асимптотики для чисел В_п и G_n , _r при г = const, п ^ от [11] [12]:

ln Вп = п(1пп — ln ln п — 1 + о(1)),

In ^G n,r

=0 - 1)

п 1пп + О(п).

Тогда ln [G^ 1 =

Вп  )

--п ln п + п ln ln п + О(п) ^ г

—от,

G 2 ^п^

□

так что —^--> 0 при п ^ от.

Предложение 9. Пусть L — модальная логика, такая что Тп П ConFr L = 0 для любого п G N. Для любого фиксированного г G N, lim P(| domMC(Fn(L))| ф г) = 0.

п^ж

Доказательство. Заметим, что любому разбиению [п] на непересекающиеся подмножества соответствует хотя бы одна шкала в Т_п П ConFr L . Действительно, если {U i , ..., U k } — разбиение, то для любого j = 1, ..., к существует связная шкала F j G Т^- । 0 ConFrL. Построим шкалу F G Т_п П Fr L , поместив шкалу, изоморфную F j , на U j для j = 1, ..., к. Разным разбиениям соответствуют разные шкалы, так что \F_n П Fr L | ф В_п.

Оценим сверху число шкал F G П_п П FrL, у которых | domMC(F )| ф г. Так как dom МС(F ) — максимальная компонента связности, у всех таких шкал каждая компонента связности имеет мощность не более г. Каждая такая шкала однозначно задаётся разбиением ^[п]/^ф = {U i , ..., U k } па компоненты связности, где к ф п i1 \U j | ф г для любого j = 1, ..., к. ii сужениями R \ U j на все компоненты связности U j . Для любого j существует 2^|U.|2 ф 2^r2 отношений на U j . Тогда искомое число шкал оценивается сверху выражением

£   2^1 1 2 • ... • 2 ^ 1 2 ф £   2^2 =G_n r 2^ 2 .

Vj |U . | ф г                               Vj |U| ф г

По предложению 8 выполнено G_n , _r2^nr 2 = о(В_п), п ^ от. Тогда

|{F G7■_nП Fr L : | domMC (F )\ ф г}|    о(В_п )

P(| domMC (F „ ( L ))| ф г) = ------ ^п---      '         V Л =       ^ о, п ^ от.

\{F_n П Fr L }|                 В_п

□

Теорема 1. Пусть L — модальная логика, такая что Т_п ПConFr L = 0 для любого п G N. Тогда Las С Log^as(ConFr L ).

Доказательство. Пусть у? 0 Log^as(ConFr L ). Тогда существуют m G N и q G [0,1), такие что P(F_n(ConFr L ) |= у) < q при п ^ m.

По предложению 5,

P(Fn(L) = у) < P(MC(Fn(L)) = у)

< P(| dom MC(F_n( L ))| MC (F_n(L))| >  m Л MC (F „ (L)) = у).

По предложению 9, первое слагаемое стремится к нулю при п ^ от. Оценим второе, используя предложение 7:

P(| domMC(F_n(L))| >  m Л MC(F_n( L )) = у) =

=   ^   P(domMC(Fn(L)) = U Л MC(Fn(L)) = у) = и c[H |U l>m

=   ^   P(MC (F_n( L )) = у | dom MC(F_n( L )) = U ) P(dom MC(F_n(L)) = U ) =

U C[H |U l^ m

=   ^   P(F_|U | (ConFr L) = у)P(dom MC (F „ (L)) = U ) <

U C [ n ] , |U \^ m

<   ^   q P(dom MC(F„(L)) = U) = иC[H |Ul^m

= q ^   P(dom MC (F_n(L) = U ) =

U C [ n ] , |U l^ m

= q P(| dom MC(F_n(L)\ >  m) <  q.

Таким образом,

P(Fn(L)= у) < o(1) + q, п ^от, так что при достаточно большом п данная вероятность меньше единицы. Тогда у 0 Las.

В силу произвольности у 0 Log^as(ConFr L), имеем L^as С ConFr L.   □

3.    Логика SLas

Шкалы Крипке из класса Fr SL будем называть SL-шкалами. В этом разделе мы опишем стурктуру случайной SL-шкалы и докажем основной результат — равенство SLas = SL.

Предложение 11. Пусть F = (X, R) — шкала Крипке. Логика SL общезначима в F тогда и только тогда, когда

Va G X (|R(a)| = 1).                                        (2)

Доказательство. Формула □р ^ Ср определяет условие Va G X (R(a) = 0), а формула Ср ^ □р — условие Va G X (|R(a)| < 1). Обе эквивалентности проверяются непосредственно по определению 7.   □

Определение 23. Шкала F = (X, R) называется обратным деревом, если:

• 1)    существует единственная точка ao G X, такая что R(ao) = 0;

• 2)    |R(a)| = 1 для л гобой a G X \ {ao};

• 3)    aR*ao для л гобой a G X.

Точку ao будем называть> корнем дерева F и обоз начать root F.

Определение 24. Пусть F = (X, R) — обратиое дерево, |X| <  от. Высотой F назовём число height F = max [k ^ 0 | 3a G X : aR^k (root F )}.

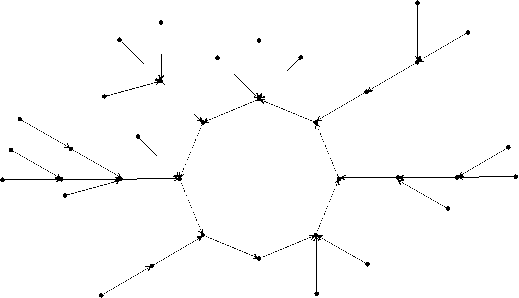
Рис. 1. Конечная связная SL-шкала

Предложение 12. Шкала Крипке F = (X,R) —конечная связная SL-шкала тогда и только тогда, когда

• 1)    в F существует цикл С = {с 1 , ..., C k } С X :

R(с 1 ) = {C2}; R^ ) = {сз}; ...; R(с k ) = {щ};                    (3)

• 2)    для любой с G С существует подмножество Т (с) С X, такое что с G Т (с) л (Т(с),R \ Т (с)) — обратное дерево:

• 3)    множества Т (с), с G С, попарно не пересекаются н образуют разбиение X.

Доказательство. Пусть шкала F = (X,R) удовлетворяет условиям 1 — 3. Покажем, что для любой точки a G X выполнено (2). Если a G С, то |R(a)| = 1 согласно (3). Иначе, a G Т (с) для некоторого с G С. Так как a G С, имеем a = с, так что a не является корнем обратного дерева Т(с). Тогда |R(a)| = 1. В силу произвольности a G X, утверждение доказано.

Обратно, пусть F = (X,R) G Т_п О ConFr SL. Покажем, что в F существует цикл. Рассмотрим произвольную точку ai G X. По условию (2) существует единственная точка a2 G R(a i ). Продолжим построение: для любого i G N существует единственная точка a t+i G R(a t ). Тогда a^|+i G {ai, ..., a^|} в силу конечности множества X. Выберем минимальное т, такое что a_m +i = a k для некоторого к С т. Тогда С = {a k , a k+i , ..., a_m } — искомый цикл.

Покажем, что цикл С единственный. Предположим, что в F существуют два различных цикла С = {с1, ..., Ck} и С ‘ = {с'1, ..., с',}. Если С ОС ‘ = 0. то a = сУ для некоторых i G [к], j G [s\. Но тогда по (2) получаем, что сц mod k)+i = с'^ modk)+i, откуда по индукции можно доказать, что С = С'. Если С О С' = 0, то заметим, что в силу связности шкалы F верно Ci(R U R-i)*с'i. Так как циклы не пересекаются, часть пути из с1 в с'1 лежит вне oiбоях циклов: Ci(R U R-i)a1(R U R-1')a2(R U R-i)... ai(R U R—^dj для некоторых i G [к], j G [s] 11 a1, ..., ai G С UС'. Так как R(сi) = {с^ modk)+1}, невозможно. что aRai, так что aiRсi. Аналогинно. так как |R(ai)| = 1, получаем a2Rai. Рассуждая таким образом, получим, что ^RaiR... RaiR^, но это противоречит тому, что R(сj) = {с(j modk)+i}. Следовательно, никл С единственный.

Рассмотрим произвольную точку с G С. Пусть Т 1 ( с ) = R^-1(с) \ С. Тогда для любой a G Т ₁ (с), R(a) = {с}. Пусть Т ₂ (с) = R ^-1 (Т ₁ (с)). Так как R(Т ₁ (с)) = {с} 11с G Т ₁ (с), имеем Т 2 (с) ОТ1(с) = 0. Заметим, что Т 2 (с) ОС = 0. Действительно, если a G Т 2 (с) ОС, то aRb алл некоторого b G R1(с), но в то же время в силу (3) R(a) = {с'} для пекоторого с' G С — противоречие. Продолжим построение: для любого i ^ 2 положим Т {+1 (с) = R ^-1 (Т г (с)). Аналогично описанному случаю доказывается, что R+i ОС = 0 и Т +i О Т у = 0 для 1 С j С i.

Положим Т (с) = {с} U U£i Т_i(c). Обозначим R_c = R \ Т (с). Докажем, что (Т (c),R_c) — обратное дерево с корнем с. По построению с € Т (с) и Т(с) О С = {с}. Так как R(c) С С, получаем, что R_c(c) = 0. Для любого a € Т(с) \ {с}, lR(a)l = 1 по (2) и R(a) С Т(с) по построению, так что |R_c(a)| = 1. Выше мы показали, что для любого a € Т1(с) выполнено aRc. Так как Т_{i +1} (c) = R ^-1 (Т_i(c)) для всех i ^ 1, отсюда следует, что aR*c для любого a € Т(с) ii любого i ^ 1, так что aR*c. Следовательно. aR*c для любой a € Т(с).

Покажем, что {Т(с) | с € С } - разбиение X. Пусть a € X. Рассуждая так же, как при доказательстве существования цикла, заметим, что в R*(a) содержится цикл. Так как С — единственный цикл. С С R*(a). Для любой с € С обозначим d(a,c) минимальное число d ^ 0, такое что aR^dc. Из условия (2) следует, что d(a, с) различны ,для разных с € С. Пусть с_а — точка из С с наименьшим d(a, с). Если d(a, с_а ) = 0, то a = с_а, так что a € Т(a). Иначе a € Т^с^са) С Т(са)

Теперь докажем, что a € Т (с) при с = с_а. Предположим, что a € Т (с) для некоторого с € С. Если a = с, то d(a, с) = 0 должно быть минимальным средн всех точек из С, тогда с_а = с. Иначе, a € Т_г (с) для некоторого г >  0, тогда aR¹"с. В силу минимальности d(a,c_а), г > d(a, с_а). Тогда путь из a в с проходит через с_а, следовательно, с_а € Т(с). По построению Т(с) ОС = {с}, так что с_а = с. Утверждение доказано. □

Определение 25. Определим шкалу X := (N, S), где S = {(n, n + 1) In € N}.

Предложение 13. [8] SL = Log X.

Предложение 14. Пусть р € ML \ SL — модальна я формула, md(р) = т. Если в шкале F = (X,R) € Fr SL найдётся простая цепь из т + 1 элемента, то F = ^.

Доказательство. По утверждению 13, (N, S) |= р. Тогда для некоторой оценки V шкалы X и некоторого г € N верно X,V,r |= р. По лемме 1, X ^{C m}, V. ^ ¹, г = р. Заметим, что dom X ^ = {г, г + 1, ..., г + т}.

Пусть ao, ..., a_m — простая цепь в F. По условию (2), R(ai) = {ai+i} для всех 0 С i < т. Тогда F ^ m = ({ao, ..., a_m}, {(a_i, a_i +₁ )m ₌ - }). Определим оценку V ‘ на F ^c ₀ ^m : положим

• V ‘(р) = {ai | 0 С i Ст, (г + i) € Vа ) ^m(p)}.

Тогда отмеченные модели (X ^{C m}, V _r ^{C m}, г) и (F C¹ , V‘, a) изоморфны, так что по предложению 2 F ^{C m}, V‘, a |= р. По лемме 1, F = р. □

Следствие 1. Пусть р € ML \ SL, md(р) = т. Пусть F = ([n],R) € ConFr SL. Обозначим С С [n] цикл oF, h = mаxheight(Т (с)). Если Ю| + h> т, то F = р.

сОС

Доказательство. Пусть |С| + h> т. Существует с € С, така я что height Т (с) = h. Тогда в Т (с) найдёте я точка a o , такая что R*(ao) — простая цепь из не менее нем т + 1 элемента.. □

Следствие 2. Пусть р € ML \ SL, md(р) = т. Пусть F = ([n], R) € ConFr SL, С С [n] — цикл в F, d = max |Т(с)|. Если d < —, то F = р.

сОС                 m

Доказательство. Пусть d < m• Так как {Т(с) | с € С} — разбиение множества [n], n = £ |Т(с)| С |СI max |Т(с)| = |С|d < |С|n,

„              сое                      ^т сОС тогда. |С| > m— = т,. следов;ательно |С| + d > т. По следствию 1. F |= р. □

Далее мы покажем, что Log^as(ConFr SL ) С SL . По следствию 1 достаточно показать, что в случайной шкале F_—(ConFr SL) с ненулевой асимптотической вероятностью найдётся большой цикл или дерево большой высоты. Исследуем распределение высоты максимального дерева, в F_n (ConFr SL ).

Определение 27. Пусть F = ([n],R) —связная SL-шкала с циклом С и разбиением {Т (с) | с Е С} на обратные деревья. Обозначим:

m := max{heightT (с) | с ЕС}, со := min{c Е С | height Т(с) = m}.

Определим МТ(F ) := F \ Т (со) — обратное дерево в F, обладающее минимальным номером корня среди обратных деревьев максимальной высоты в F.

Определение 28. Определим случайную шкалу Т_п = МТ (F„(ConFr SL )).

Определение 29. Для любого U С N, IU | < го, а Е U обозначим Т(U,r) множество обратных деревьев вида (U, R) с корнем г.

Предложение 15. Пусть п Е N, U С [п] — фиксированное подмножество, |U| < го, r Е U. При условии dom Т_п = U, root Т_п = r случайная шкала Т_п равномерно распределена на Т(U, г) :

Р(Т_П = Т 1 | domT¹_n = U, rootT'_n = г) = Р(Т¹_П = Т 2 | domT’_n = U, rootT'_n = г)

ДЛЯ любых Т 1 , Т 2 Е Ти,а.

Доказательство. Пусть Т 1 = (U, S1), Т ₂ = (U, S2) Е Т и, _а. По определению условной вероятности достаточно показать, что

Р(Т = Т1 Л dom^ = U Л root Тп = а) = Р(Т = Т2 Л domТп = U Л root Тп = а), что равносильно

|{F Е R_n П ConFr SL : МТ(F ) =ТД| = |{F Е R_n П ConFr SL : МТ(F ) =Т2}| .

Построим биекцию f между этими двумя множествами. Пусть F = ([n],R) — связная SL-шка.та II МТ(F) = Т1. В частпости, root МТ(F) = rootT1 = а. Определим f(F) = ([n],R‘), где

aR^,b ^^

{ aRb, aS 2 b,

если а Е U если а Е U.

Иными словами, мы заменили отношение на множестве U так, чтобы на нём находилось дерево Т2 вместо дерева Т 1 . Так как rootT2 = а = root МТ(F ), то легко убедиться. что f(F ) — свтюная SL-шка.та е таким же разбиением на обратные деревья, как 11 F.

Тогда domМТ (F ) = U н МТ(F ) = (U, R ‘ \U ) = (U, S2) = Т 2 .

Чтобы показать, что f — биекция, заметим, что для любой связной SL-шка.ты G = ([n],R‘). такой что МТ(F ) = U и G \ U = Т2. прообраз f -1(G) можно вычислить аналогичной заменой отношения на множестве U на отношение дерева Т 1 :

f 1(G) = ([n],R). г;те aRb ^^

( а^Ь, ( aS 1 b,

если а Е U если а Е U.

□

Определение 30. Для любых U С N, |U | < го, и а Е U обозначим X(U,a') случайный элемент множества Т(U,a') с равномерным распределением.

Определение 31. Обозначим Y_n случайный элемент с равномерным распределением на всех обратных деревьях вида ([п], R).

Следствие 3. Пусть п Е N, U С [п] — фиксированное подмножество, а Е U. Тогда для любого Т Е Т(U,a):

Р(Т_п = Т | dom Т_п = U, root Т_п = а) = P(X(U, а) = Т).

Предложение 16. Пусть U С N. Тогда для любого a G U и любого числа h G N,

P(heightX(U,a) = h) = P(height Jt/ । = h).

Доказательство. Так как |U| < той распределение X(U, a) не зависит от структуры множества U, достаточно рассмотреть случаи U = [п]. где п G N.

По определению, Y_n равномерно распределено на множестве |JP=1 Т (Ы,^г). Тогда для любого h G N:

a=1 \^{T ([ n ] ,a)}\

Пусть a, b G [п]. Обозначим a_{a -} b циклический сдвиг на [п], который переводит b в a :

^ a - b : [п] м [п]; a a - b (i) = (i + a - b) mod п

Для любого Fa = ([n],R) G Т([п], a) определим Fb = ([n],R‘), где iR’j ^^ ^a-b(i)R^a-b(j).

По построению root Fb = b, так что F b G Т([п],Ь); деревья F_a и F b изоморфны, так что height F_a и height Fb. Легко видеть, что данное преобразование F_a м F b обратимо: аналогичным образом применим к Fb обратный циклический сдвиг оь — a,- Таким образом, для любых a, b G [п] ii лк:>бого h G N определена 6iюкпия между {F G Т ([n],a) : heightF = h} ii {F G Т ([п],Ь) : height F = h}. Следовательно.

\{F GT ([п], a) : height F = h}\ = \{F GT ([п], b) : height F = h}\, a, b G [п].     (6)

Аналогично,

• \^{T ([п],a)}\ = \^{T ([п],b)}\^{, a,b G [п]}.                                   (6)

Тогда по (4) для любого h G N:

P(height Ц = h) = "\{F GT([п|' Д ^ F = h}\ = п\Т (п, 1)\

= \{ ^{F GT} ( ^[nl^, 1): height ^F = ^{h }}\ = P_(heig_ht х_(И 1 = h).

\ T (п, 1)

Для любого a G [п] 11 h G N, используя (о) ii (6):

{F G T([n],a) : height F = h}\

P(heightX ([n],a) = h) =                               =

^{T ( n,a )}

= ЮЮЖЩЦещН^^ = p   J,, = h),

\ T (п, 1)

что и требовалось доказать. □

Следствие 4. Пусть п G N, U С [п] — фиксированное подмножество, a G U. Тогда для любого h G N:

P(heightT, = h \ domT, = U, root Т_п = a) = P(heightY|^। = h).

Доказательство. Утверждение прямо вытекает из следствия 3 и предложения 16.   □

Предложение 17. [13] Справедливы асимптотические выражения для математического ожидания и дисперсии высоты случайного дерева:

E(height УД ~ УУлп

Var(height Y_n) ~

л(л — 3)п

п м то.

Предложение 18. Log^as(ConFr SL ) С SL.

Доказательство. Пусть ? 0 SL , md(?) = т.

По следствиям 1 и 2,

P(F_n(ConFr SL ) = 9?) > P

т

- . п _      _ ~          \ dom Тга| > — Л height Тп > т) .   (7)

Вычислим второе слагаемое, используя следствие 4:

п dom Тп | > — Л height Тп > т) =

=   ^   P(dom Тп = U Л height Тп > т) = и с[Н ^ |> %

=   ^   P(height Тп >т | domТп = U) P(domТп = U) = иси |и|>%

=    ^   P(heightY|u| > т)P(domif1n = U) = и си |и|> %

= P(height Yu| > т) •    ^   P(domif’n = U) = иси |и|>%

= P(height у_и | > т) P (| dom^ < ^) .

Для любого к >  ^ верна асимптотика ^^= = О (^) = о(1), ^{так что по} утверждению 17 и неравенству Чебышёва получим

P(height Yk ^ т) < P Н height Y k — E height Y k | > E height Y k — т) <

Var(height Y_k )         л (л — 3)к

л(л — 3) л — 3

∼∼

³(^ — ^ )^{2   6}

п ^ от.

⩽∼

(E height Y k — т)²    3(у^2лк — т)²

Тогда для любого U С [п], |U| > ^ выполнено:

P(heightYu | >т) > Л — ^—л³ J (1 + о(1)) = 9-—^(1 + о(1)), п ^ от.

Обозначим q := 9-Д > 0. Подставим полученную оценку в (7):

п                            п\

P(F_n(ConFr SL ) =?) ^ P ^| domF^ < — J + q(1 + o(1)) P ^| domJ^ ^ — J =

=P

(| dom^| < т_) + q(i + _O(1)) ^1 — p

(| dom^ <-)) = т

= ^q + (1 — q) P (| dom^ <т) ) (1 + ⁰(1)) ^ q(1 + ⁰(1)).

При достаточно большом п эта вероятность положительна.

В силу произвольности ? 0 SL , Log^as(ConFr SL ) С SL .    □

Теорема 2. SL ^as = SL .

Доказательство. Заметим, что F_n О ConFr SL = 0 для лгобого п G N: цикл на множестве [п] является связной SL-шкалой. Тогда по теореме 1 и утверждению 18, SL ^as С ConFr SL С SL . По утвер^кдешпо 3. SL С SL ^as. □

4.    Заключение

Мы доказали, что SLas = SL. Ключевую роль в доказательстве сыграла теорема 1, которая позволила вместо всех SL-шкал рассматривать только связные SL-шкалы, комбинаторные свойства которых значительно проще. Предложение 12 показывает, что связная SL-шкала может быть описана небольшим набором параметров. Такое описание позволяет нам явно вычислить вероятности возникновения свойств, от которых зависит логика случайной SL-шкалы.

Исследование может быть продолжено в нескольких направлениях. Открыт вопрос о законе нуля и единицы для модальных формул в SL-шкалах. Полученный нами результат может послужить важной отправной точкой для изучения закона нуля и единицы. Поскольку SLas = SL, достаточно установить, существуют ли формулы, не входящие в логику SL, которые выполиены в случайной SL-шкале с положительной, но меньшей единицы асимптотической вероятностью.

Описанный нами метод может быть использован для изучения вероятностных свойств других модальных логик. В частности, можно рассматривать логики, описывающие более широкие классы шкал, чем SL. Условие (2) является частным случаем условий вида Уж (|г(ж)| С т) ил и Уж (1 С |й(^)| С ел), которые соответствуют модальным логикам Alt m И DAlt _m [9]. Мы предполагаем, что случайные шкалы этих логик обладают схожими свойствами, что позволит обобщить подход данной статьи на эти логики.