Подгруппы, содержащие тор, связанные с полем отношений кольца с однозначным разложением

ПОДГРУППЫ, СОДЕРЖАЩИЕ ТОР, СВЯЗАННЫЕ

С ПОЛЕМ ОТНОШЕНИЙ КОЛЬЦА С ОДНОЗНАЧНЫМ РАЗЛОЖЕНИЕМ

Н. А. Джусоева, В. А. Койбаев

Работа посвящена изучению подгрупп полной линейной группы, содержащих иеращепимый максимальный тор, для случая, когда основное поле является полем отношений кольца с однозначным разложением (факториального кольца). Основным результатом работы является построение максимальных подгрупп указанного вида.

Вопросы описания некоторых классов подгрупп линейных групп являются важными вопросами теории групп. Данная работа, посвящена, изучению подгрупп полной линейной группы, содержащих иеращепимый максимальный тор, для случая, когда, основное поле является полем отношений кольца с однозначным разложением (факториального кольца). Основным результатом работы является (теоремы 4.7, 4.8) построение максимальных подгрупп указанного вида.

Вопросам подобных исследований были посвящены работы 3. И. Боревича, В. П. Платонова, Г. Зейтца, А. А. Бондаренко, Чан Нгок Хоя, С. Л. Крупецкого и др. (см. [1-4]).

• § 1.    Введение

Пусть к — поле, К — конечное расширение степени п поля к. Имеет место регулярное вложение

К* ед АЫДА), а о fa мультипликативной группы К* поля К в группу всех fe-линейных автоморфизмов поля К, рассматриваемого как fe-линейное пространство, где /а(ж) = ax, х Е К.

Образ К* при указанном вложении мы называем нерасщепимым максимальным то-ромТ(К) = ТДДк\ Если выбрать базис поля К над к, то, очевидно, АиЦ(А) изоморфно полной линейной группе ОТД, к), при этом тор ТДД будет представлен некоторой подгруппой матриц в группе ОТД, к).

Рассмотрим теперь случай, когда, поле К определяется в качестве расширения поля к неприводимым над к многочленом х¹¹ — р, р Е к. Выбрав в качестве базиса. К над

Работа выпонена при финансовой поддержке Министерства образования РФ, грант № Е02-1.0-79.

к : 1,0, ...,О^{п х}, где 6 = Др — корень многочлена ж^п — /z, мы видим, что тор Т^К) представляется (в выбранном базисе) группой матриц С(ж), ж Е к^п \ {б}, где

	/ жх	МЖ„	МЖ„-1  .	•  ^Ж2\
	ж2	Ж1	№	■ МЖз
СД) =	Жз	Ж 2	Ж1	. /гжг
	\ж„	Ж„-1	Ж„-2   •	■ ■ Ж1 /

Так как в описанном случае мы имеем радикальное расширение поля к, К = к) Др), то тор мы будем обозначать через Т = T(/z).

В данной работе мы рассматриваем следующий случай. Под R понимается целостное кольцо с единицей 1, в котором выполняется однозначное разложение на простые (факториальное кольцо). Далее, через к мы обозначаем поле отношений кольца R. На протяжении всей работы d = ру .. .p_m Е R — элемент кольца R, который является произведением различных простых из R Д свободно от квадратов).

Как хорошо известно, согласно критерию Эйзенштейна многочлен х^п — d неприводим над полем к. Поэтому мы имеем радикальное расширение К = к) Vd), р = d, степени п поля к. При этом тор обозначается через Т = ТД).

Мы рассматриваем подгруппы Н полной линейной группы G = СЕД, к), содержащие нерасщепимый максимальный тор

Т = ТД) = {С(ж) : ж Е ^^п\{0}}.

Напомним определение сети (см. [1]). Система ст = (щД, 1 <  i,j < п, аддитивных подгрупп поля к называется сетью порядка п, если

^ir^rj С <7у при всех значениях г, г, j.

Для произвольной сети ст порядка п через МД) обозначается совокупность всех тех матриц a = («у) порядка п с элементами из к, для которых atj Е ар при всех г и j. Ясно, что МД) — подкольцо в кольце МД, к) всех матриц порядка п над к.

Далее, если р Е Р — простой элемент кольца R, то обозначаем

R^ := {— Е к : (m,n) = Д,р) = 1}

— множество всех p-целых элементов поля отношений к кольца R. Очевидно, что R^ — максимальное подкольцо поля к.

В работе мы пользуемся следующими обозначениями. Выше были определены матрицы СД) = (су). Ясно, что элементы Су матрицы СД) определяются формулами

СВ

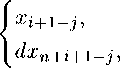
j < Е j ^ i + 1.

Далее, через Е = е обозначается единичная матрица; ву — матрица, у которой на позиции (цД стоит 1, а на остальных местах нули; £у(а) = е + аер — элементарная трансвекция, г Ду dr(e) = е + Д — 1)етт, в Д 0; [ж,у]=жуж ху 1

• § 2.    Подгруппы, содержащие элементарную трансвекцию

В дальнейшем через Н мы обозначаем промежуточную подгруппу, Т < Н < G = GL^n,^, содержащую элементарную трансвекцию ty(«), i 7^ j, о? G k, a ^ 0.

С каждой подгруппой H связаны модули

Aij ⁼ Ai^H^ = {a G k : tij^a) G Я}, i ^ j.

Очевидно, что А^ являются подгруппами аддитивной группы к* поля к.

Лемма 2.1. Пусть тор Т нормализует подгруппу Н. Положим Ai = Ад = Ад (И), г > 2. Тогда, модули А^ (г ^ j) определяются по формуле:

. _                  j < к,

(dAnдiдд —j, j > i

(ср. С (1)).

• <    Имеем Л21 = А₂. Покажем, например, что А₂ = Л21 = Л₃2 = ... = A^n-i- Последние равенства вытекают из соотношений

ct2i(a)c-1 = t32(a), c2t2i(a)c"2 = t43(a), ..., с(п-2^21(«)с"(п"2) = tn,n-4(a), где с = с(жо), жо = (0,1, 0,... , 0). >

Предложение 2.2. Пусть о = (сцД — сеть аддитивных подгрупп поля к, М(о) — соответствующее сетевое кольцо. Пусть do^j С ст^ для всех i,j. Если тор Т нормализует сетевое кольцо Мф), то сеть о имеет вид

(А^ dAn dAn-д .. dA2\ ^2 Ад dAn . йЛ3 СУ = Аз А‘2 Ад . . сМ4 (2) Un Ате—1 Ап — 2 • • Ад) где Ai = суд, г = 1,2,..., п. При этом

Ад С А₂ С ... С A_n, dA_n С Ад.

• <    Для внедиагональных позиций доказательство вытекает из леммы 2.1 (достаточно брать cacijc^-1'). Далее, равенство Ад = судд = сг₂2 = ... = ст_пп очевидно достигается последовательным сопряжением матрицы аед (a Е Ад = судд) с. помощью матрицы с = с(жо), где жо = (0,1, 0,... , 0). Покажем теперь включения, указанные в предложении. Пусть ж = (1,1,0,... , 0). Тогда с = с(ж) и

• с"1 = с-1(ж) = ---       ,0^^

v '   1 + (-1)П+Ч где у = (1, -1,... , (-1)"+1).

Пусть а Е суд = Ai, 1 <  г < n— 1, аед Е Мф^). Рассмотрим матрицу саедс^-1 Е Мф^). Имеем

L        h+1,1 i + (_i)n+i^’ поэтому a           _

1 + (-1)"+Ч е 1+1 “

Отсюда a Е A₊i, следовательно, Л_г С Д-щ. Далее, пусть /3 Е А_п = a„i, Pe_ni Е МД). Тогда

Нещс-^и = 1 + (_1)п+ч G МДУ откуда dp Е сгц = Ai, следовательно, dAn С А^. >

В дальнейшем мы считаем, что Ai,... , А_п — идеалы некоторого подкольца Л поля к, причем Ai С ... С А_п, dA_n С А^. Если тор Т нормализует сетевое кольцо МДУ то тор Т нормализует сетевую группу ОД) = (е + МД)) П ОВД, А). По этой причине ввиду предложения 2.2 мы в дальнейшем для идеалов А^ рассматриваем сети вида (2).

Лемма 2.3. Пусть ст = Д^^) — сеть вида- (2). Тогда

• (а)    если г — г ^ к — s, то ст_кб С ст_гг:

• (Ь)    если п + р — г) > к — s, то do^g С суд;

• (с)    если п — р — г) + Д — s) < 0, то ст_к8 С da;_r.

• <    Имеем

J Д₊1-₅,      8 < к,            J Л+1-r,     г <  г,

^Ап+к+1_8, 8^ к + 1,       ^dAn+m_r, т>г + 1.

Доказательство теперь вытекает из того, что

Д С Д С ... С А_п, dA_n С А^ ▻

Предложение 2.4. Рассмотрим сеть ст вида. (2). Если ДД) Е Т • ОД), то Р Е ст^ j).

• <    Пусть, например, г = 2, j = 1. Тогда ДДД = сД), для некоторых a Е ОД), сД) Е Т. Поэтому первые строки матриц а и сД) совпадают. Отсюда

$1 Е 1 + Ai, х_п Е А_п, x_n-i Е А_п_1,... , т₂ Е А^.

Поэтому сД) Е е + МД) и £₂Д/3) = сД)а^-1 Е е + МД), откуда Р Е a₂i. >

§ 3. Достаточные условия нормализуемости сетевой группы

С каждой матрицей с = сД) Е Т связана обратная матрица с^-1 = сД) = Д-) Е Т, у = (yi,..., у„) Е к^п , где yi = |^|, причем Од — алгебраическое дополнение элемента сд матрицы с^-1 = с(у).

Для элементов матрицы с-1 = с(у) имеем формулу (1):

/ J Us+l-Tl

С — х dyn+s+1_r,

г ^ s;

Г ^ 8 + 1.

Введем в рассмотрение подкольцо Rq = КД) поля к следующего вида

Ко := КД) = ring ДгУу dx_ry_s : г + j ^ п + 1, г + s > n + 1). хек^п\б

Следующая теорема дает достаточные условия нормализуемости сетевой группы тором.

Теорема 3.1. Пусть Л — подкольцо поля к, содержащее кольцо Rq = R(d), причем d Е Л. Пусть, далее, о = (<7у) — сеть идеалов вида. (2), где Л_г — идеалы кольца. Л, причем Hi С ... С И„ и dA_n С Ai. Тогда, тор Т = T(d) нормализует сетевую группу G(a), а. потому J = Т • G(o) — промежуточная подгруппа, содержащая тор Т, причем ^согласно 2.4) Aij^H) = <Ту, i ^ j.

• <    Пусть g = е + a Е G(a), где a = («у) Е М^оУ Пусть, далее, с = (су) = с(ж), с"¹ = (сС) = с(у). Покажем, что b = (ЬгД = мае^-1 Е М^. Достаточно показать, что если a = a_kse_ks, где a_ks Е a_ks, то b = сас^-1 Е М(а), т. е., что Ьц Е оц для всех i,r. Имеем Ьц = Cikak_sc'_sr. Покажем, что

• ^r = cikaksdST Е оц.                                  (4)

В силу формул (1) и (3) для сц, и c'_ST нужно рассмотреть четыре случая (а = г+ 4 —к, (3 = s + 1 — г):

• (a)    s < г - 1, к < г, c_ika_ksc'_ST = x_ada_ksy_u^y,

• (b)    s < г - 1, к ^ г + 1, c_ika_ksd_sr = dx_n+ada_k8y_n+y,

• (с)    s ^ г, к < г, сда_к8с'_8т = х_аа_к8уу;

• (d)    s ^ г, к ^ г + 5, c_ika_ksd_sr = dx_n^_aa_ksyy.

Имеем:

(г — г) — (А: — s) = а + /3 — 2,(5)

п + (г — г) — (а — s) = п + а + /3 — 2,(6)

п — (г — г) + (к — s) = п — (а + /3) + 2.(7)

(а): Имеем а > 1, п + /3 ^ 1. Тогда п + аТ/З — 0^8,а потому в силу (6) и леммы 2.3 (Ь) имеем do_ks С щ_г. Если а + (п + /3) ^ n + 1, то ж_ау_п+^ Е Ro, а потому имеем (4). Если же а + (п + /3) >n +1, то « + /3 — 2^4, а потому, согласно (5) и 2.3 (a) o_ks С щ_г, но dx_ay_n+y Е Ro отсюда следует (4).

• (Ь) : Если (п + а) + (п + /3) ^ n + 1 (см. определание Rq), то включение (4) очевидно. Если же (п + а) + (п + /3) > n + 1, то из (6) и 2.3 (Ь) имеем do_ks С а_гг, но dx_n+ay_n+^ Е Rq. Отсюда следует (4).

(d): Рассматривается симметрично случаю (а). >

§ 4. Максимальные нетривиальные промежуточные подгруппы группы GL^n,^

В этом параграфе мы построим максимальные нетривиальные (не содержащие SL(n,, к)) подгруппы группы G = GL^n,^, содержащие тор Т = T(d). Напомним, что к — поле отношений кольца R с. однозначным разложением на. простые, d Е R, d является произведением различных простых.

Лемма 4.1. Пусть р — простой делитель элемента, d, p\d; xi,...,x_n Е R. Если р^к\ с(ж)|, ТО p\xi, ... ,р\х_к.

• <    Индукция по к. Для к = 1 лемма очевидна. Пусть лемма справедлива для Д — 1). Пусть р^к\ с(ж)|. Тогда по индукционному предположению р\ху,... ,p\xk-i. Следовательно, с(ж) = ж^"¹ + р^к • s, s Е R. Поэтому, если р^к\ с(ж)|, то т?|ж&. >

Лемма 4.2. Пусть выполнены условия леммы 4.1 и пусть р|жх,... ,р|ж/;. Тогда

• (а)    если г < п — к, то р^к\Сц,

• (Ь)    если i > п — к, то р^к-1\Сц,

здесь Си — алгебраическое дополнение элемента сц.

• <    Не умоляя общности положим: i = 1, к = п — 1 в случае (а) и г = пД = n - 1 в случае (Ь). Проверка этих случаев не составляет сложности. >

Напомним, что с матрицей с = с(ж) связана обратная матрица с^-1 = с(у) = (сС), где у = (ух,... , у„) и yi = |^|, Си — алгебраическое дополнение элемента сц матрицы С = (су) = с(ж).

Теорема 4.3. Для всякого простого делителя р элемента d имеет место включение

Ro С R^y где R^ — кольцо всех p-целых элементов поля отношений к кольца, с однозначным разложением R.

• <    Для доказательства теоремы нам достаточно показать (см. определение кольца Ro), что если г + j Д n + 1, то x^yj Е R^ и если г + j > n + 1, то dxiyj Е R^py

Заметим прежде всего, что x^yj = ^^-j , а потому в числителе и знаменателе находятся однородные многочлены степени п. Поэтому в силу формулы для однородного многочлена у:

Wx-ц-. . Дж„) = ДДжх,... ,ж„)

мы можем считать, что жх,..., ж„ Е R, причем (жх,... , ж„) = 1.

Пусть р^к \ с(ж) и р^к+1 ) с(ж)|. Тогда в силу леммы 4.1 р|жх,...рД^. Так как (жх,... , ж„) = 1, то к < п — 1. Рассмотрим хууу.

Ввиду леммы 4.2 имеем p^k-1\Cij, далее p\d, а потому р не входит в канонический знаменатель элемента dxiyj, следовательно, dxiyj Е Rq. Поэтому рассмотрим случай i+j Д п + 1. Если j = п — к, то согласно лемме 4.2 (а) имеем р^СД, а потому р не входит в канонический знаменатель элемента Xiyy откуда x^yj Е R^p Пусть j > п — к. Тогда 4.2(b) влечет p^k-1\Cij. Далее, так как г + j < n + 1, то j < n + 1 — i, но из n — к < j следует n — к < n + 1 — г, откуда г Д к. Так как р|жх,... , р|жд., то р|ж_г. Следовательно, р не входит в канонический знаменатель элемента x^yj = _с(Д , откуда x^yj Е Н^рЦ >

Из теорем 3.1 и 4.3 вытекает следующая теорема.

Теорема 4.4. Пусть р — простой делитель элемента d, p\d. Рассмотрим сеть о_р

Тогда тор Т = ТД) нормализует сетевую группу СД_Р), а. потому Н_р = Т-СД_Р) является промежуточной подгруппой группы С = СЕД, к), содержащей тор Т. Далее, Н_р не содержит 8ТД,к), точнее Ау^Нр) = (сг_р)у, г Д j.

Лемма 4.5. Пусть выполнены условия теоремы 4.4. Пусть Т < Н < G, причем Н ^ Нр. Пусть, далее, Aij = A^^HY i ^ j. Тогда А 2 = ... = А_п = А — подкольцо поля к, содержащее Ro, где А^ = Ац, i ^ 2, следовательно, либо А = R^, либо А = к.

• <    Отметим, что А^ связаны с А_т соотношениями из леммы 2.1. Имеем

VklACk ^i(«)] = Д1(£«), к^1, к^1,1^1.                 (8)

Если I < к, a Е Ац и так как Я;(1) Е Н, то (£ = 1) из (8) следует, что a Е А^, а потому А; С А^. Если же I > к, a Е Ар то так как tki^p) Е Н, то (£ = р) из (8) следует, что рА( С А^. Таким образом,

Rpp С А2 С ... С A_n, pA_n С А^.

Очевидно также, что p^mA_n С А₂, т ^ 1. Покажем теперв, что А^ = ... = А_п. Если A_n = R^p то последние равенства очевидны. Пуств A_n 2 R^pp Тогда так как dr(,R*_p^ с Я, то ^ G Л„, s > 1. Но p^mA_n С А„_1, откуда. 1 Е р⁸ A_n С А_п__х. Пуств теперв В Е А_п. В силу леммы 2.1 A_n_i_jn = рА_п, далее, р⁸А_п = р ■ p^s~¹A_n С рА^ С рА_п, откуда. 1 Е p^sA_n С рА_п = А_П_1_1П, т. е. i_n_i _n(l) Е Н. Согласно формуле

[^.„(l),^)]^-!,!^);

MBi имеем /3 Е A_n_yi = A_n_i. Таким образом, A_n С A_n_i и A_n_i = А_п. Рассуждая аналогично, мы получим: А₂ = ... = А_п = А. Далее, в силу соотношения

[^32(«)Д21(^)] = Д1(оф)

MBi имеем А2 С А³, а. потому АА = А. Таким образом, А — кольцо, R^ С А С к. >

Лемма 4.6. Пусть р — простое, p\d, Н_р = TG^o_pY Если Н, Т ^ Н ^ G, причем Н 2 Нр, то Н A SL(,n,kY

• <    Согласно лемме 4.5 нам достаточно показать, что подкольцо А строго содержит R^pP В силу леммы 4.5 и формулы

^rs^ds^t^s^dp^^^pHrs) = Д_г \Р7

нам достаточно показать, что £_rs(l) для некоторых г < s или t_ST ^^ Е Н для s > г.

Итак, пусть a Е Н, а ^. Н_р.

Так как Н D G(o"_p), то умножая матрицу а слева, на. элементарные трансвекции из G^Op) и диагональные матрицы из ф(Я*_р)) С G^o_p) и на. скалярную матрицу из Т мы можем считать, что

/ 1 рт'2 . . . рт« \ а= .°. РЛ ’                              (9)

\ О О ... р^к- /

• т. е. ац = 1, ац = p^kl, г ^ 2, ац = р^т*, г ^ 2, а^ = 0, i > j. Сделаем ряд замечаний.

Можно считать, что mt < 0, иначе умножая матрицу а справа, на. tu^— р^т‘ ) на. позиции (1,г) мы получим нулевой элемент.

Можно считать, что mt ^ mj для г < j, так как иначе, умножая матрицу а справа, на. tij(~p^mJ~^m‘) на. позиции (1Д) мы получим нулевой элемент.

Итак, будем считать, что

О > 7712 ^ "7 g > ... > тп.(10)

Имеем 1 + р Е R*_py а потому b = [а^-1,Д(1 + р)] Е Н. Матрица b отличается от единичной только первой строкой, которая равна (1,р^тз+1,... ,р^тп+Д Поэтому

• п —1п—1

п Ыр^т1"^т’^ь П Ы-р^т-"^тд = ti„(p^m"⁺¹) G н.

г=1г=2

Если mn + l < 0, то в силу замечания сделанного в начале доказательства Е А. Поэтому пусть тп + 1 > 1, тп ^ 0. Тогда из (10) мы имеем m2 = т^ = ... = тп = 0. Покажем, что кп = 0. Действительно, аНп(р)а-1 = НДр1"^'1), «"^„(pja = ^Др^1^.

Снова в силу замечания сделанного в начале доказательства можно считать, что 1 — к_п ^ 1 и к_п + 1 >  1, откуда к_п = 0. Если 77 = 2, то доказательство завершено, так как (см. (9)) 7772 = ^2 = 0, а потому £12(1) Е Н. Поэтому будем считать, ЧТО 77 > 3.

Покажем теперь, что к^ = 0. Имеем (см. (9): «12 = 1, ann = 1, «22 = ркД a£2n(p)a~1£in(-p) = ^«(Р4'241) G Н.

В силу замечания сделанного в начале доказательства, к^ ^ 0. Пусть к^ ^ 1, тогда. (°12 = "Р^

121(1)« 1 ^2п(рк)^21(~ 1) = £1Д — 1) G Н и наше утверждение доказано. Поэтому будем считать, что ^ = 0.

Таким образом в матрице а (см. (9)) мы можем считать, что «ц = 1, < > 1; к^ = 0, «22 = 1; кп = 0, «„„ = 1; «у = 0 для г > j. Следовательно, для обратной (треугольной) матрицы а-1 : «Д = «Д = «Д = 1, «Д = — 1- Положим b = iff [а-1^21(1)] :

тогда. 6£„₂(1Д^-1 = £12(1) G Н и в силу замечания, сделанного в начале доказательства, лемма. 4.6 доказана. >

Теорема 4.7. Для всякого простого делителя р элемента d группа Н_р = T(d(G(a_p( является максимальной нетривиальной (не содержащей 8ЬД, к)) подгруппой полной линейной группы G = GL(n, к), содержащей тор Т = T(d(.

• < Пусть Н_р Д Н < G. Покажем, что Н = G. Для этого в силу леммы 4.6. нам достаточно показать, что ВД,к( С Н. Так как ВД^^Д С Н, то нам достаточно показать, что d_T ^^ Е Н для некоторого 1 < г < 77. Действительно, так как Т < Н, то для ж = (0,1, 0,... , 0) мы имеем с(Д Е Н. Умножая матрицу с(ж) на. матрицы перестановки из SL(n,k( С Н и на. d_r( — 1), мы получим, что d_r(d( Е Н, откуда, так как ВД^Н^ С Н, то d_r(p( Е Н и d_T ^^ Е Н. Теорема, доказана. >

Отметим интересное следствие из теоремы 4.7.

Теорема 4.8. Для всякого простого р Е R группа Нр = T(p(G(ap( является максимальной нетривиальной подгруппой группы G, содержащей тор Т(р(.