Подход к оценке частоты спектральной составляющей цифрового сигнала по спектру с низким разрешением

Спектральное представление X ( f ) сигнала x ( t ), получаемое с использованием преобразования Фурье, получило широкое распространение в сфере вибрационной диагностики оборудования и является базовым инструментом для дальнейшей обработки и анализа сигналов вибрации, полученных с первичных измерительных преобразователей [1]. В идеальном случае i -я периодическая компонента сигнала x ( t ) отображается на спектре соответствующей линией (точкой на графике), абсцисса которой равна частоте компоненты f i , а ордината – амплитуде X fi [2]. В реальных условиях спектр сигнала имеет конечное разрешение по частоте df , из-за которого энергия периодической компоненты будет распределена между несколькими соседними линиями (точками) в окрестности x i (рис. 1). Данное явление известно как растекание спектра [3]. В результате частота f k наибольшей по амплитуде линии в окрестности x i не равна частоте f i спектральной компоненты, а амплитуда X f_k данной точки не будет равна амплитуде X f_i данной спектральной компоненты. Ошибка | f i – f k | достигает своего максимального значения, равного df /2, при равных амплитудах X fk и X fk+ 1 .

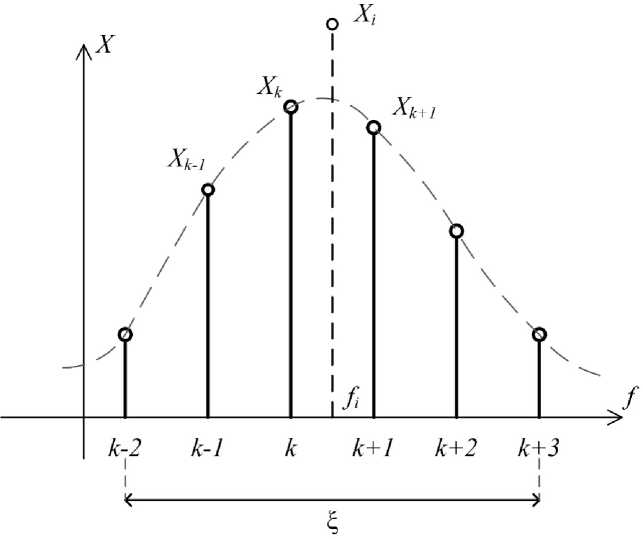
Рис. 1. Спектральная компонента на графике спектра сигнала Fig. 1. Spectral component on the signal spectrum graph

При этом существует ряд задач вибродиагностики, для решения которых необходимо знать частоту спектральной компоненты сигнала с высокой точностью: для детектирования дефектов ротора требуется точное значение частоты вращения, а для детектирования дефектов подшипника качения нужны точные значения их характерных частот (частоты перекатывания тел качения по внутреннему и внешнему кольцам, частота сепаратора и т. д.), которые, в свою очередь, также зависят от частоты вращения [4–6].

1.    Разрешение спектра по частоте

Спектр сигнала позволяет представить сигнал в виде совокупности его частотных составляющих с информацией об их амплитуде и фазе. Важный параметр спектра – разрешение по частоте df , фактически являющееся расстоянием в герцах между двумя соседними линиями спектра.

Алгоритмы преобразования Фурье относятся к анализу в диапазоне частот от 0 до частоты Найквиста. Разрешение в таком случае определяется количеством спектральных линий в этом диапазоне [7]. Таким образом, df определяет, насколько точно можно оценить частоту составляющих сигнала.

Также разрешение спектра связано с длительностью интервала наблюдения [8, 9]:

df = 1/ T = 1/( L / F s ) = F s / L , (1)

где τ – длительность сигнала в секундах; F S – частота дискретизации; L – количество отсчетов в сигнале (согласно теореме Котельникова – Найквиста – Шеннона [10]). Таким образом, естественный способ увеличить разрешение спектра – увеличить длительность анализируемого сигнала.

Рассмотрим это явление на примере простого гармонического сигнала [11], состоящего из двух синусоидальных компонент: 10 и 15 Гц с амплитудами 6 и 3 соответственно. Пусть частота дискретизации F S 1 будет равна 16 000 Гц, а количество отсчетов в сигнале L 1 – 32 768. Также рассмотрим спектры этого сигнала, уменьшив параметры F S 1 и L 1 вдвое: F S 2 = F S 1 /2, L 2 = L 1 /2. Построим 4 графика спектра этого сигнала (рис. 2), изменяя параметры количества отсчетов и частоты дискретизации.

Как следует из формулы (1), наилучшее разрешение было получено на том спектре, где F S наименьшее, а L – наибольшее.

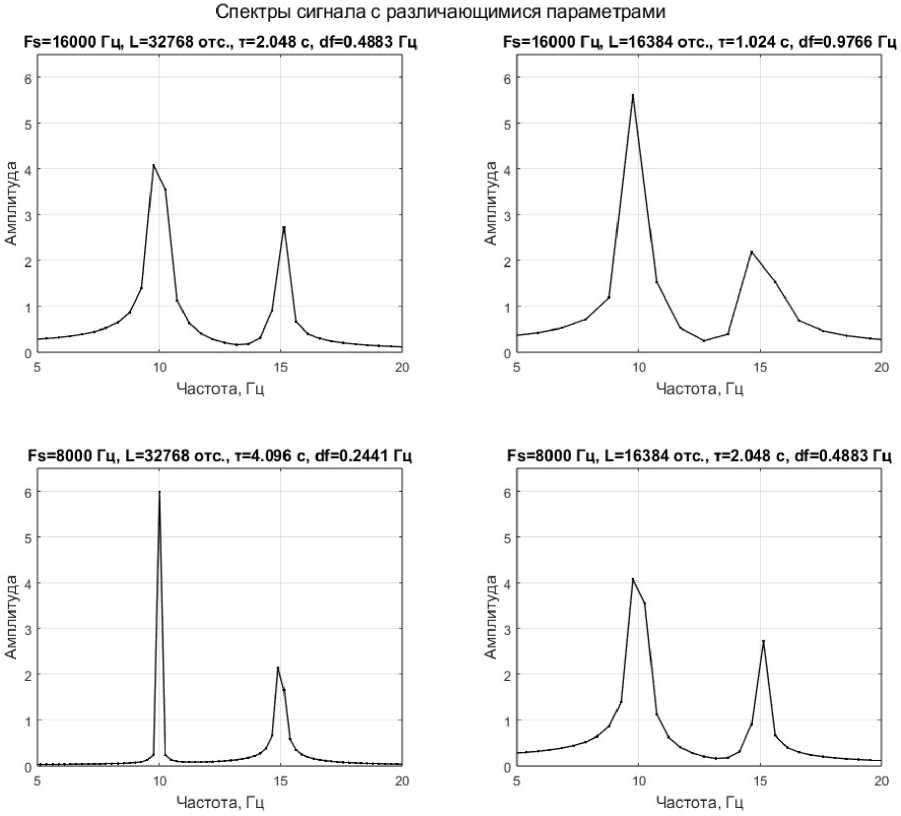
Рис. 2. Спектры гармонического сигнала с различающимися параметрами Fig. 2. Harmonic signal spectra with different parameters

Параметры, влияющие на разрешение спектра, тесно связаны с возможностями измерительного прибора, записывающего сигнал [12]. Увеличение длительности записи сигнала приводит к увеличению расхода энергии, что может быть особенно критично для приборов с автономным батарейным питанием, и к росту объема передаваемых и хранимых данных [13]. Уменьшение частоты дискретизации, напротив, снижает объем данных при увеличении разрешения получаемого спектра, однако при этом пропорционально уменьшается максимальная детектируемая датчиком частота. На практике параметры F _S и L выбираются исходя из требуемого режима работы и характеристик измерительного прибора, в связи с чем уточненная оценка частоты спектральных компонент спектра с недостаточным разрешением является актуальной с практической точки зрения.

2.    Методы уточнения частоты пика по спектру

Будем рассматривать нижеописанные методы на примере синтезированного гармонического сигнала:

s ( t ) = A sin(2 n ft + ф ), (2) где A – амплитуда сигнала; f – частота; φ – фаза. Выберем следующие параметры: A = 0,5; f = 16,27 Гц; φ = 2/π. Длительность сигнала пусть равняется 0,5 секунды. Частота дискретизации при построении спектра равна 16 000 Гц, количество отсчетов спектра – 32 000. Таким образом, шаг по частоте составляет 0,5 Гц. Временное представление сигнала и его спектр представлены на рис. 3.

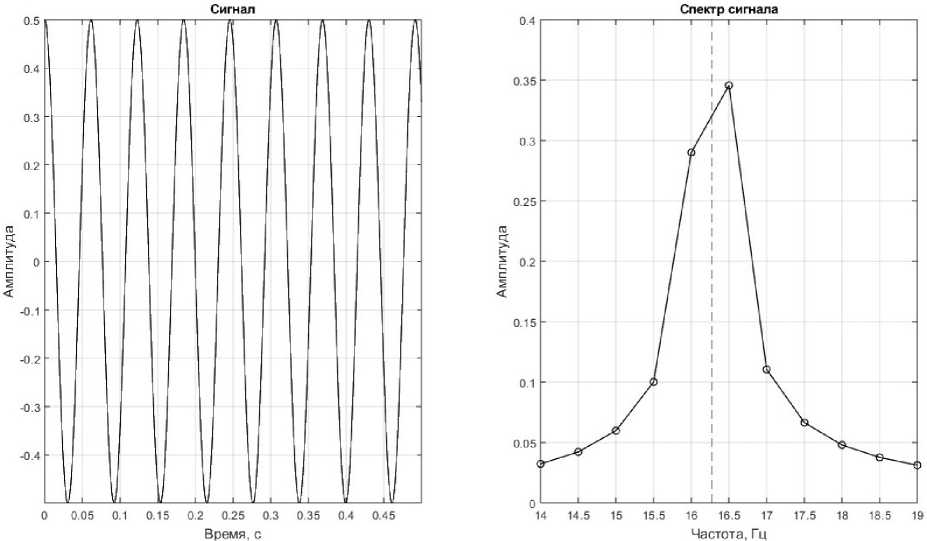
Рис. 3. Исследуемый гармонический сигнал c компонентой 16,27 Гц Fig. 3. The tested harmonic signal with a component of 16.27 Hz

• 2.1.    Параболическая интерполяция

• 2.2.    Частотная демодуляция

В случае, когда повышение разрешения целого спектра невозможно, можно прибегнуть к повышению разрешения его участка, взяв максимум и две соседние точки спектра (см. рис. 3) [14]. Тогда искомая частота спектра может быть найдена, даже если она расположена между двумя дискретными линиями спектра, путем вычисления максимальной абсциссы интерполяционной кривой пика дискретного спектра.

Точки спектра с координатами (16; 0,29), (16,5; 0,345) и (17; 0,11) примем за решения уравнения параболы. Подставив в уравнение координаты точек и решив систему уравнений, получаем оценочное значение f i (абсциссу вершины параболы) (рис. 4) [15].

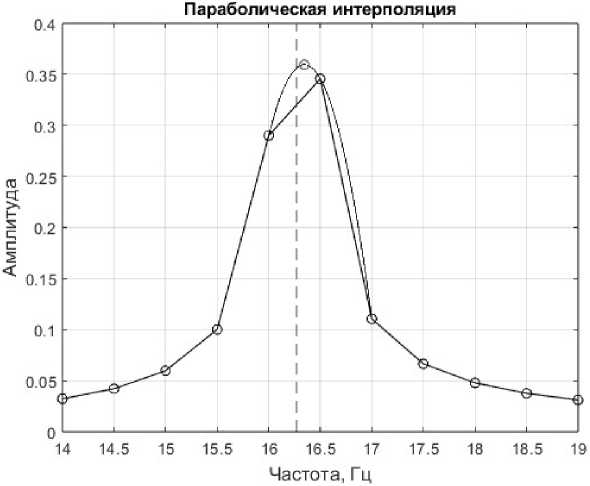
Рис. 4. Спектр исследуемого сигнала с выделенными узлами интерполяции Fig. 4. The spectrum of the tested signal with highlighted interpolation nodes

Значение частоты на вершине параболы равно 16,35 Гц. Отклонение от реального значения 16,27 Гц составляет 0,4645 %. Несмотря на достаточно высокое отклонение, следует отметить простоту и скорость выполнения данного метода, что является его главным достоинством.

Еще один метод уточнения частоты связан с частотной демодуляцией сигнала.

Предварительно из полного сигнала x ( t ) нужно выделить модулированный сигнал a ( t ) путем фильтрации в окрестностях интересующей частоты. Затем, согласно [16], определяем трансформанту Гильберта ã ( t ) для a ( t ):

• a(t) = H {a(t)} =1 ” a(t) —dt.(3)

n -” t -t

Полученная трансформанта Гильберта связана с исходным модулированным сигналом a ( t ) и аналитическим сигналом â ( t ) следующей формулой:

• ci = a (t) + ja (t).(4)

Представим аналитический сигнал в виде

• a( t) = a (t) ejф( t).(5)

Из (5) выделим составляющую фазовой модуляции e ^{j φ( t )} и устраним составляющую с несущей частотой f ₀ путем умножения на e ^{– j 2π f 0 t} . Результирующая функция φ( t ) ^{–2π f 0 t} является модулирующим по фазе сигналом, который, если выражен по модулю 2π, нуждается в дополнительной обработке для определения непрерывного сигнала φ m ( t ).

После получения непрерывного сигнала φm(t) из него может быть получен модулирующий по частоте сигнал fm(t) по формуле f (t) = Xd^m(tl.                                                                (6)

• ^{m (} ) 2 n dt

После выполнения описанного алгоритма получим вектор мгновенных частот f m ( t ), из которого можно получить частоту компоненты, применяя методы статистической обработки, к которым относятся среднее арифметическое, медиана, мода [17]. Применим вышеописанный алгоритм к сигналу, описанному в пункте 2.1. Получим вектор мгновенных частот, изображенный на рис. 5.

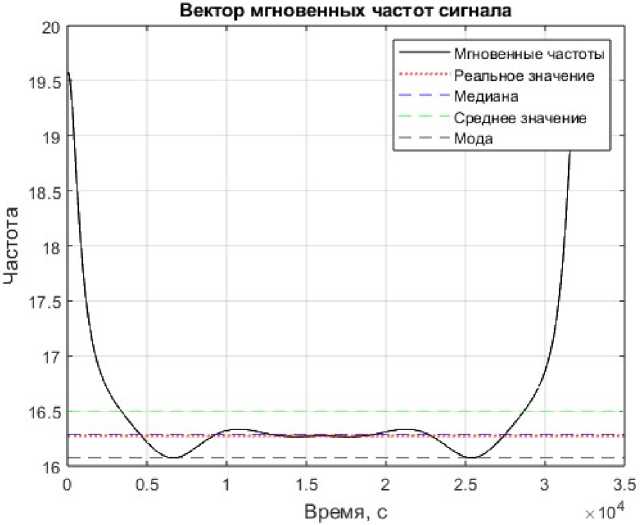
Рис. 5. Вектор мгновенных частот сигнала

Fig. 5. The vector of instantaneous signal frequencies

Красной пунктирной линией на графике отображено реальное значение частоты. Применим разные методы статистической обработки и занесем результаты в таблицу.

Полученные значения частоты Obtained frequency values

Метод статистической обработки	Полученное значение, Гц	Отклонение, %
Среднее арифметическое	16,4999	1,4131
Мода	16,0743	1,2028
Медиана	16,2857	0,0965

Получение значения частоты из вектора мгновенных частот с помощью медианы показало наименьшее отклонение.

Недостатком вышеописанного метода является сложность выбора диапазона фильтрации для выделения модулированного сигнала: результат не будет соответствовать желаемой точности как в случае попадания в диапазон более одной компоненты сигнала, т. е. при избыточной ширине диапазона, так и в случае неполного попадания компоненты, т. е. при недостаточной ширине диапазона. Проблема выбора диапазона фильтрации для данного метода заслуживает отдельного рассмотрения.

При этом существенным преимуществом данного метода является высокая точность получаемого результата в сравнении с методами интерполяции. Его независимость от частоты дискретизации позволяет применять метод даже для спектров с существенно низким разрешением ( df больше 0,5 Гц).

Заключение

Были рассмотрены и проверены на практике две группы методов уточнения частоты по спектру: основанных на интерполяции и на частотной демодуляции. По результатам проверки на смоделированном гармоническом сигнале можно сделать вывод о том, что метод параболической интерполяции легок в реализации, состоит из меньшего количества шагов и не требует сложных расчетов. Полученный данным методом результат оказался менее точным, его отклонение от реального значения частоты составило 0,4645 %. Более высокую точность показывает метод частотной демодуляции: при расчете частоты через медиану вектора мгновенных частот отклонение составило всего 0,0965 %. Однако он требует большего количества сложных расчетов.

Таким образом, в случаях, когда важна максимально возможная точность полученного значения частоты, следует применять метод частотной демодуляции, а в случаях, когда скорость и простота вычислений более важны, чем точность, например, при реализации концепции краевых вычислений (edge computing) с выполнением расчетов на борту интеллектуальных датчиков, следует применять параболическую интерполяцию.

В дальнейшей работе над методами уточнения частоты по спектру с недостаточным разрешением будут исследованы другие методы интерполяции, например, интерполяция с помощью формулы Гаусса. Также будет исследована возможность улучшения получаемых описанными методами результатов с помощью дополнения спектра нулями (zero-padding). В рамках продолжения исследований в области получения информации об отдельных частотных составляющих сложного сигнала планируется исследовать возможность получения точной амплитуды интересующей компоненты.