Подход к систематизации алгоритмов

Создание алгоритмов связано с проектированием и моделированием. Онтологии алгоритмов могут относиться к области онтологий проектирования [1] или к онтологии моделирования [2]. Сравнивая концепции, описанные в указанных работах, по большему числу признаков онтологии алгоритмов следует отнести к онтологиям моделирования. В то же время, точка зрения авторов данной статьи отличается от принципов, изложенных в работе [2]. После концептуальной модели автор этой работы ставит объектную и трансформационную модели. В реальности каждый алгоритм обладает функциональностью, которая в работе [2] не рассматривается. Именно функциональность отражает главную роль алгоритма. Аспект функциональности в работе [2] не отражен, но это вполне объяснимо, поскольку она ориентирована в первую очередь на ситуационное управление и во вторую на моделирование, а не на алгоритмы. Другая сторона создания алгоритмов связана с их технологической направленностью на обработку информации и прямо не связана с онтологической составляющей. В известной работе Т. Кормена [3], многократно переизданной [4], на которую существует более 4000 ссылок, заложены канонические основы построения алгоритмов. Эти основы направлены на методы вычислений. Однако в книге слабо представлен системный анализ.

Достаточно отметить, что базовым принципом построения алгоритмов во введении поставлен эвристический принцип «разделяй и властвуй». Де-факто это относит такой подход в область эвристики и когнитивного анализа. Но эти аспекты не рассматриваются в работе [3]. По мнению авторов данной статьи, современные алгоритмы можно рассматривать как сложные системы, поскольку они обладают многими соответствующими признаками. Алгоритм можно отнести к классу закрытых детерминированных сложных систем, и, используя подход Месаровича [5], можно отметить свойство функциональности как одну из миссий сложной системы и миссий алгоритма. В настоящее время развиваются сложные системы с переменной структурой. Однако алгоритмы имеют устойчивые связи и относятся к системам с постоянной структурой. Определение сложных систем, даваемое в работах по системному анализу Месаровичем [5], Берталанфи [6] и Уемовым [7], определяет их как системы, имеющие совокупность устойчивых связей. Это полностью соответствует представлению об алгоритмах. Вместе с тем, во многих работах алгоритм, как объективный феномен, связывают лишь с обработкой информации, тогда как в широком смысле он, безусловно, является носителем знания и средством познания. В книге Н. Моисеева [8], изданной ещё до выхода работы [3], алгоритмы рассматриваются с логическо-познавательных позиций как схема эволюции, а не как вычислительный механизм. Такая точка зрения приближает алгоритм к онтологии. Алгоритм можно рассматривать как зафиксированное знание, которое воспринимается разными людьми и может передаваться от одного человека к другому. Совокупность алгоритмов, решающих родственные задачи, даёт возможность делать научное обобщение, которое выходит за рамки технического решения задачи. Это даёт основание связывать алгоритмы с онтологиями и говорить об онтологии алгоритмов. Цель данной статьи - попытка описания онтологий алгоритмов и их систематика с онтологических позиций.

1    Материалы и методы

Материалами для написания данной работы послужили многочисленные описания алгоритмов и схем решения вычислительных и логических задач. В качестве методов использован системный анализ, категориальный анализ, логический анализ.

• 1.1    Топологические модели алгоритмов. Систематика алгоритмов

Обобщая различные схемы алгоритмов и применяя системно-категориальный анализ [9] можно выделить определённые группы алгоритмов по признаку сходства и разные группы по признаку различия. Построение алгоритмов связано с функциональными преобразованиями. Простейшее функциональное преобразование входной информации X в выходную информацию Y с помощью функции f имеет вид

• (1)     Y = f ( X ),

или в логической форме

• (2)    X → Y .

По этой причине алгоритмы, которые относятся к группе, описываемой выражениями (1) и (2), называют прямыми или сквозными [10]. Кроме того, возможны линейные и нелинейные алгоритмы. Это разделение обусловлено топологической схемой алгоритма. Если схема представляет собой последовательную цепочку (ациклический граф), то такой алгоритм является линейным. Схема в выражении (2) может описывать один процесс или совокупность последовательных процессов. Это описание линейных алгоритмов [11]. Линейные алгоритмы могут иметь разную длину, но имеют один маршрут вычислений.

Если топологическая структура алгоритма представляет собой сложную сеть с циклами и ветвлениями, то такой алгоритм называют нелинейным. Нелинейные алгоритмы могут иметь много маршрутов вычислений. Это ставит дополнительную задачу оптимизации таких вычислений, или сетевую оптимизацию. На рисунке 1 приведены три простые схемы алгоритмов. Они являются линейными, поскольку обработка информации осуществляется «сверху-вниз» последовательно и линейно. Между ними существуют качественные различия.

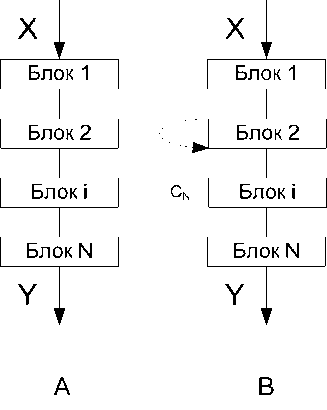
Рисунок 1 - Три схемы линейных алгоритмов

А – сквозной (Al 1 ); B – циклический (Al 2 ); C – стратифицированный (Al 3 );

Алгоритм со схемой, представленной на рисунке 1А, называют «сквозным» или «прямым». Он используется в основном при количественной обработке информации. Часто он представляет собой совокупность параллельных веток и служит основой параллельной обработки информации [12]. Формально его описание имеет следующий вид

• (3)     Al 1 : F ( X ) → Y .

• (4)    ( ∃ Al 1 ( X ) →{ F ( X ) → Y }.

Выражение (3) используется в системном анализе и говорит о том, что система Al 1 осуществляет F - функциональное преобразование Х в Y. При этом выражение (3) описывает линейные и нелинейные преобразования и представляет собой «чёрный ящик» по отношению к пользователю. Оно описывает, в том числе, и искусственные нейронные сети и относится к схемам на рисунках 1А и 1В.

Алгоритм на рисунке 1В называют «циклическим» или «с условием». Формально его описание имеет следующий вид

• (5)     Al 2 : F (( X , n , δ )) → Y ( n , δ ),

где n – число циклов, δ - погрешность.

Недостатком циклического алгоритма является возможность зацикливания или зависания. Эти ситуации возникают, если алгоритм составлен некорректно или если происходит компьютерный сбой. Алгоритмы на рисунках 1А и 1В имеют один вход и один выход.

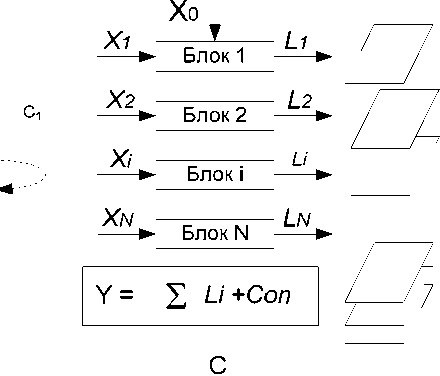
Алгоритм на рисунке 1С называют «стратифицированным». Он содержит множество входов и такое же количество выходов. Его описание имеет следующий вид

• (6)     Al 3 = Σ Al i ,

где i = 1 …n – количество слоёв L .

Выражение (6) означает, что общий алгоритм стратифицированной обработки Al 3 представляет собой сумму частных алгоритмов, каждый из которых имеет свой вход и выход, но в совокупности они обрабатывают общий исходный массив Х.

• (7)    Al i : F i ( X i )→ L i .

Выражение (7) означает, что частный алгоритм обработки Al i преобразует входное подмножество X i в выходное подмножество L i , к оторое представляет собой слой в общей системе слоев.

• (8)    Y = Σ L i + Con ( i , j ).

Выражение (8) означает, что результат обработки Y представляет собой сумму результатов L i , и множество связей между ними Con ( i , j ) [13].

Общая топологическая схема всех алгоритмов, представленных на рисунке 1, приведена рисунке 2. Эта схема соответствует обобщённому описанию (1), (2). Простейший алгоритм имеет один блок обработки.

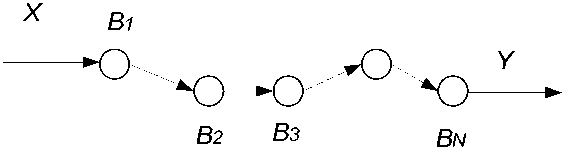
Рисунок 2 - Общая топологическая схема линейных алгоритмов

X – входная информация; Y - результат (выходная информация);

Bi - функциональный блок, содержащий функцию обработки f i .

На рисунке 3 приведён пример топологической схемы нелинейного алгоритма. Схема на рисунке 3 c учётом ориентации дуг графа условно имеет два циклических контура. При рассмотрении графа как не ориентированного число циклов многократно возрастает.

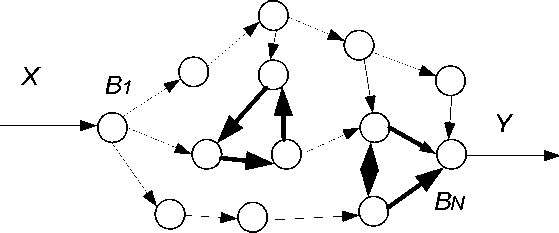
Рисунок 3 – Пример топологической схемы нелинейного алгоритма

Такая схема на практике имеет множество разновидностей. Две из них представлены на рисунке 4 – это схемы итеративного (А) и линейного инкрементного (В) алгоритмов.

Итеративный и инкрементный алгоритмы имеют сходство и различие со стратифицированным алгоритмом (рисунок 1С). При их использовании задаётся некое начальное условие X 0 базовое входное множество X 1 и совокупность входных множеств X i . Это первое принципиальное отличие. В линейных алгоритмах входное множество одно.

Итеративный алгоритм (рисунок 4А) имеет следующее описание:

• (9)     Al 4 = Σ Al i ,

где i = 1 „.n - количество итераций;

• (10)    Al i : F i ( X i )^ Y i + d i .

  

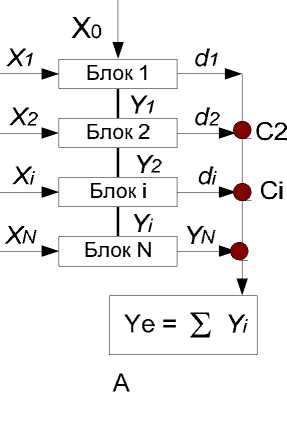
  Рисунок 4 - Итеративный (А - Al 4 ) и инкрементный (В - Al₅) алгоритмы

  
  
  
  
  

Выражение (10) означает, что частный алгоритм обработки Al i преобразует входное подмножество X i в выходное подмножество Y i плюс итерационную добавку d i - аддитивную часть в общем выходном множестве Y . Результат вычислений на этапе и итерация объединяются в точках слияния C i . Вычисления происходят по двум контурам: основному ( Y i ) и вспомогательному ( d i )

• (11)    Y = S ( Y i +d i ).

Для итеративных алгоритмов существует проблема сходимости [14]. Она состоит в том, что не при всяких начальных условиях X о результат вычислений сходится. Сходимость возможна, если lim i ., ( d i ) = 0.

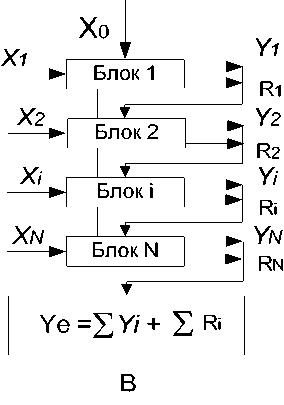
Инкрементный алгоритм (рисунок 4В) имеет следующее описание

• (12)    Al 5 = S Al i ,

где i = 1^n - количество инкрементных операций:

• (13)    Al i : F i [ X i + R ( i -1) ] ^ Y i + R i .

Выражение (13) означает, что общий алгоритм инкрементной обработки Al 5 представляет собой сумму частных алгоритмов, как при стратифицированной (3) и итеративной (6) обработке. Результат инкрементной обработки представляет собой сумму частных решений и сумму полученных ресурсов, которые не являются решением, но служат инструментом для возможно решения и анализа других задач:

• (14)    Y = S ( Y i + R i ).

Выражение (14) означает, что частный алгоритм обработки Ali преобразует входное подмножество Xi в выходное подмножествоYi, и создаёт дополнительный ресурс Ri, который используют на последующем этапе обработки информации. Т.е. результат инкрементной обработки Y представляет собой аддитивное множество Y плюс некий дополнительный информационный ресурс R, который можно использовать при решении других задач. Алгоритм на рисунке 4В называют линейным в силу того, что он последовательно решает задачу без возврата к предыдущим этапам. Алгоритм Al5 является в большей степени «онтологичным» в сравнении с другими алгоритмами, поскольку ресурс может представлять собой новое описание, новое знание и новый метод.

Существует модификация инкрементного алгоритма, которую называют «спиральной» или «циклической». Этот алгоритм приведён на рисунке 5. Модификация показывает, что каждая версия приближает результат к области решения задачи.

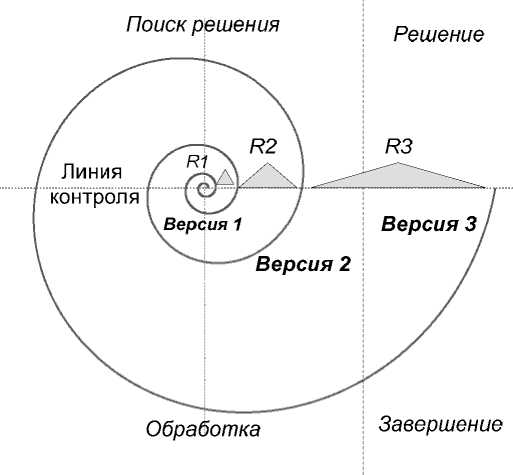
Рисунок 5 - Спиральная схема инкрементного алгоритма (Al6)

Инкрементный спиральный алгоритм имеет описание, аналогичное (12):

• (15)    Al 6 = Σ Al i .

Выражение (15) означает, что общий алгоритм обработки Al представляет собой сумму частных алгоритмов, как при линейной инкрементной обработке (13). Здесь i = 1 …n – количество инкрементных операций:

IncA : f(A(X, n)) → Σ S i + Σ S j , i=1..n, j=1..n-1, S i - частные решения на каждом шаге

• (16)    Al i : F i [ X i + R ( i -1) + C i -1 ] → Y i + R i + C i .

Здесь: Y i – частное решение, R i - частный ресурс, C i – частное новое условие на i -ом шаге; IncA – обозначение инкрементной обработки.

Выражение (16) означает, что частный алгоритм обработки Al i реализует версию преобразования входного подмножества X i в выходное подмножество Y i и создаёт дополнительный ресурс R i , который используют в следующей версии обработки информации. Дополнительно на каждом витке спирали (шаге инкремента) формируется дополнительное условие решения задачи, которое расширяет направление спирали и меняет вектор решения¹. Обработка осуществляется с возвратом к исходным условиям, но с применением дополнительных ресурсов и дополнительных условий:

• (17)    Y = Σ [ Y i + R i )] + Σ C j .

Выражение (17) означает, что результат инкрементной обработки Y представляет собой аддитивное множество, в которое интегрирован инкрементный ресурс, накапливаемый при реализации каждой версии обработки. Алгоритм на рисунке 5 называют спиральным в силу того, что он циклически решает задачу с возвратом к предыдущим этапам, но с наращивани- ем ресурса решения задачи и изменением (уточнением) исходных условий. Спираль раскручивается до тех пор, пока очередная версия не попадёт в область решения. Алгоритм на рисунке 5 описывает, в том числе, и генетические алгоритмы.

• 1.2 Технология сортировки

Сортировка является типичным алгоритмом количественной [3] и качественной обработки информации. Его схема приведена на рисунке 6.

Сортировка преобразует входное гетерогенное неклас-

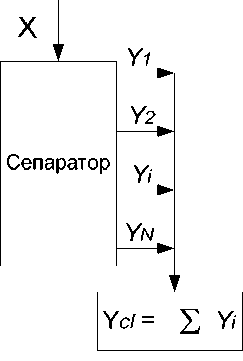
Рисунок 6 - Алгоритм сортировки

сифицированное множество X в совокупность классифицированных однородных множеств Y i . Алгоритм сортировки достаточно прост и имеет следующее описание. Объект А принадлежит классу ClassI (класс i) , если содержат те же элементы, что и в классе ClassI .

• (18)    ∀ x { x ∈ A &  x ∈ ClassI } → А ⊂ ClassI ,

где∀ – квантор общности, → - знак «следует». Приведённая запись читается так: «Множество А принадлежит классу ClassI, если для каждого элемента множества х, принадлежащего множеству А, следует принадлежность этого же элемента х множеству ClassI». Особенность выражения (18) в том, что оно позволяет осуществлять качественный анализ и качественную обработку. Выражение (18) позволяет соотносить объект А с определённым классом и относить объект к классу и по свойствам его элементов. Алгоритм, который описывает выражение (18), является качественным.

2    Обсуждение

Проведённый анализ позволяет говорить об общем онтологическом описании качественных и количественных алгоритмов. Если работа [3, 4] рассматривает технологическую вычислительную сторону алгоритма, то работа [8] трактует алгоритм как метод исследования и анализа эволюции. В работе [15] алгоритм применяется как инструмент анализа топологии и сложности, что также далеко от чистых вычислений и приближает это понятие к познавательному образу. Замечательным представляются исследования [15] комплексного представления проблем обработки предметно-ориентированных знаний (в научно-технической сфере), построения и проектирования «знание-ориентированных информационных систем с онтолого-управляемой архитектурой» [16] как нового класса средств вычислительной техники. Авторы прямо не употребляют термин «алгоритм», но в работе они рассматривают информационную технологию компьютерной обработки (алгоритм), технологию автоматизированной обработки предметно-ориентированных знаний (алгоритм), т.е. сущность работы в «онтологически – алгоритмических методах». Существует направление качественных алгоритмов [17], применяемых в качественном анализе [18]. Всё это говорит о многообразии понятия алгоритм и некорректности его сведения только к вычислительным процессам.

Можно говорить об алгоритмических моделях, о том, что алгоритмические модели могут относиться , а онтологические модели всегда относятся [19] к классу познавательных моделей. Это проявляется в связанном с ними и объединяющем их когнитивном моделировании [20, 21].

Заключение

Некоторые виды схем алгоритмов несут ярко выраженные познавательные функции. Стратифицированные алгоритмы и спиральные (инкрементные) алгоритмы схематизируют познавательные процессы, которые лежат за рамками количественных вычислений. Современное развитие методов вычислений и алгоритмов требует обобщения этого направления. Развитие онтологического инжиниринга связано не только с совершенствованием методов компьютерной обработки информации, но и с развитием онтологического подхода к алгоритмам как к инструментам познания. Отсюда следует актуальность и важность разработки новых научных методов онтологии алгоритмов. Перспективным следует считать развитие методов когнитивного моделирования алгоритмов в двух направлениях: анализ процессов человеческого мышления при построении алгоритмов и алгоритмизации; анализ познавательного значения алгоритмов как инструмента извлечения новых знаний и технологий.