Подход к учету взаимодействия RANS- и LES-областей пограничного слоя в расчетах методом SST-IDDES

Использование вихреразрешающих методов, таких как метод крупных вихрей (LES — Large Eddy Simulation) и прямое численное моделирование турбулентности (DNS — Direct Numerical Simulation), до сих пор является невозможным для прикладных расчетов пристенных течений, так как для этого требуется слишком большое количество вычислительных ресурсов. Решение системы осредненных по Рейнольдсу уравнений Навье-Стокса (RANS — Reynolds Averaged Navier-Stokes) значительно дешевле, но из-за несовершенства современных моделей турбулентности не дает возможности надежно описывать отрывы. Кроме того, RANS-расчеты почти не дают информации о спектральных характеристиках турбулентности. Гибридные RANS/LES-методы требуют меньшее, чем LES, количество ресурсов за счет того, что пристенная часть пограничного слоя, где для корректного применения LES требовалось бы измельчение сетки до масштабов мельчайших вихрей, моделируется в режиме RANS. При этом гибридные методы позволяют получить больше информации о турбулентности, чем классические RANS-расчеты, а также дают возможность значительного уточнения описания отрывов турбулентного пограничного слоя [1]. Таким образом, совершенствование гибридных методов и решение открытых вопросов, связанных с ними, является актуальной задачей.

В настоящее время существует большое количество различных гибридных методов (см., например, обзоры [2,3]), однако, несмотря на более чем 20-летнюю историю развития, не все проблемы, связанные с точностью их работы, решены. Наибольшие трудности представляет расчет турбулентных пограничных слоев, пристенная часть которых моделируется в режиме RANS, а внешняя часть разрешается в режиме LES. К этим недостаткам относятся сдвиг профиля средней скорости на логарифмическом участке пограничного слоя (LLM — Log-Layer Mismatch), а также заниженный коэффициент трения.

Первые упоминания проблемы LLM появились еще в 2000 г. в работе [4], в которой проводился расчет течения в канале на базе уравнений метода отсоединенных вихрей (DES — Detached Eddy Simulation) [5] с замыканием моделью Спаларта-Аллмараса. Было показано, что в широком диапазоне чисел Рейнольдса наблюдается несовпадение «смоделированного» и «разрешенного» участков профилей средней скорости, а коэффициент трения занижен до 22%. В дальнейшем было установлено, что некоторое влияние на величину ошибки может оказывать выбор модели турбулентности [6], переходной функции между RANS- и LES-областями и используемой численной схемы [7], а также изменение констант модели турбулентности [8]. Однако надежного и полного решения проблемы LLM до сих пор не найдено. Интересно заметить, что сдвиг в профиле скорости остается, даже если поменять RANS- и LES-области местами, то есть пристенную часть пограничного рассчитывать в режиме LES с разрешением вплоть до поверхности, а внешнюю — в режиме RANS [9].

Некоторую информацию об источниках проблем в гибридных RANS/LES-методах можно получить при помощи анализа данных DNS. Так, например, в работе [10] проводится фильтрация поля течения в канале фильтром переменной ширины, меняющейся от характерного размера шага сетки («LES-фильтрация») до размеров порядка длины канала в однородном направлении (аналог осреднения по Рейнольдсу). Таким образом исследовалось влияние дополнительных членов в уравнениях, появляющихся из-за некомму-тативности операций гибридной фильтрации и взятия производной по пространству, то есть 8f/8x j = 8f/8x j (фильтрация обозначается чертой сверху, / — произвольное поле). Некоммутативность появляется из-за изменения ширины фильтра в пространстве. Было показано, что эти дополнительные члены в области RANS/LES-перехода имеют такой же порядок величины, как и основные члены уравнений. Было сделано предположение, что пренебрежение такой некоммутативностью может быть причиной неправильного поведения профиля скорости в переходной области.

Существует несколько методов устранения проблемы LLM. Одним из наиболее популярных является использование так называемого форсинга, то есть искусственного добавления возмущений в зону перехода между RANS- и LES-областями. Это могут быть, например, стохастические возмущения [8,11-14], синтетическая турбулентность [11,15] либо возмущения, сгенерированные по данным DNS или LES [11,14]. Существенной проблемой данного метода является сложность подбора амплитуды возмущений: во многих работах используются эмпирические константы, которые нужно подбирать для конкретного типа течений, либо же для определения амплитуды используются некоторые неуниверсальные зависимости и/или нелокальные по пространству данные [12,14].

Еще одним решением является модификация поля течения на границе RANS/LES с помощью параллельного RANS-расчета [16, 17]. Использование такого метода мотивировано предположением, что нестационарное LES-решение вносит ошибки в RANS-область: модели турбулентности, используемые для RANS, не рассчитаны на правильную работу в условиях существенно нестационарного поля скорости. Недостатком данного метода является увеличение численных затрат.

В данной работе делается еще один шаг на пути к решению перечисленных проблем гибридных методов. Предлагается локальный метод стохастического форсинга, подбор амплитуды в котором основан на идее работы [10]. Будут моделироваться слагаемые в отфильтрованных уравнениях Навье-Стокса, появляющиеся из-за некоммутативности гибридного фильтра и производной по пространству в переходной области между RANS и LES. Кроме того, в RANS-области расчета предлагается использовать осредненные по времени величины для устранения влияния нестационарной части решения. Форсинг рассматривается в применении к гибридному методу IDDES (Improved Delayed Detached Eddy Simulation) [1], сформулированному на основе модели турбулентности SST [18].

Статья организована следующим образом. В разделе 2 приведено описание используемого гибридного метода и нового метода форсинга. В разделе 3 представлены результаты IDDES-расчетов пограничного слоя на плоской пластине и продемонстрирован вклад предложенной модификации в решение. В разделе 4 новый метод применен к течению за закругленной ступенькой. Статья завершается выводами по полученным результатам.

2.    Описание методов

Расчеты проводились с помощью разработанной в ЦАРИ программы zFlare [19], входящей в состав пакета EWT-ЦАГИ [20]. Для аппроксимации конвективных потоков использовалась гибридная схема, комбинирующая противопоточную схему WENO5 и центральноразностный метод второго порядка точности с помощью переходной функции из работы [21]. Диффузионные потоки аппроксимировались центрально-разностной схемой второго порядка точности. Для движения по времени использовался глобальный временной шаг и двухстадийный диагонально-неявный метод Рунге-Кутты третьего порядка точности [22]. Во всех расчетах величина шага по времени выбиралась так, чтобы число Куранта (отношение временного шага ко времени, за которое самая быстрая характеристика в газе перемещается на ячейку расчетной области) во внешней части пограничного слоя было порядка 1.

• 2.1.    Гибридный RANS/LES-метод

Используется полная отфильтрованная система уравнений для сжимаемого газа (принято правило суммирования по повторяющимся индексам):

^др + Эр^и к = ₀

at    дхк '

дрй dt дрЕ "at"

+

+

д^- ^jUk + Р^'г^'к + Р + Тк] = 0, д                                            -и'и'

д^- рЕн к + рн к + Т гк и г + q k + ри'_ги'_ки г + ри'_к + рС р Т'и'_к + т'_ки г = 0 ,

где р — плотность газа, Пк — компоненты вектора скорости, р — давление, Т — температура, С р = kR/(k — 1) — молярная теплоемкость воздуха при постоянном давлении, к = 1.4 — постоянная адиабаты для воздуха, R ~ 287.05 Дж/(кг • К) — газовая постоянная для воздуха, Е — полная энергия единицы массы газа, q ^ — молекулярный тепловой поток в к-м направлении, т_i k — тензор вязких напряжений. Здесь f — величина f, к которой применен гибридный фильтр, под f ‘д’ и f 'д'һ' понимаются центральные моменты Джермано при такой фильтрации [23]: f ‘д’ = fg — fg, f‘ д'Һ' = fgh — fgh. Форма системы уравнений (1) подразумевает, что пульсации плотности пренебрежимо малы.

Во всех расчетах газ считался совершенным, молекулярное число Прандтля Рг полагалось равным 0.72 и система уравнений (1) дополнялась следующими соотношениями:

• -    щщ п'п’      -

• Е = - - + і ^ + СТ, 2 + 2 + у
• р = pRT,

• -          (^dni   ^дпк   ^{2 дп}т \

• ^{Т 1к} = -^^(Т)       ⁺ ■ -^—3 ад⁶‘^к) ’

2.2.    Подход к учету взаимодействия RANS- и LES-областей

_ = - ц(т)Ср дт qk Рг дхк’ где Су = Ср — R, р — динамический коэффициент вязкости воздуха (формулы для р, которые использовались в расчетах, приведены в соответствующих разделах статьи).

Система уравнений (1) замыкалась в данной работе гибридной моделью SST-IDDES [24]. В этой модели решаются два дополнительных дифференциальных уравнения: для кинетической энергии отфильтрованной части турбулентных пульсаций к = піпі/2 и для их характерной частоты ш = Е/(С р к), г де е — скорость диссипации кинетической энергии турбулентности, С^ = 0.09 — эмпирическая константа. В SST-IDDES переключение между RANS- и LES-областями происходит с помощью переходной функции fd, которая входит в формулу для масштаба длины турбулентности:

Wd ES = ^f d • Ф.А NS ^{+ (1 — f} d ⁾ • ^LES.

Для Zrans ¹¹ Zles используются стандартные формулы из [24]. причем модификация Zraxs с помощью сомножителя (1 + f_e), согласно рекомендациям в [24], не делается. Взяты стандартные значения всех констант модели, кроме Спезі и Све82, которые зависят от численного метода. В данной работе используются величины Сое si = Сое S2 = 0.56, откалиброванные по методике из [25].

Как уже было отмечено во введении и будет продемонстрировано далее, в стандартной постановке модель SST-IDDES искажает профиль скорости на логарифмическом участке (проблема LLM). В следующем параграфе будет предложен способ модификации метода расчета, который решает проблему в случае турбулентного пограничного слоя на пластине.

Следуя работам [8,12], будем восполнять недостающие пульсации скорости на границе RANS- и LES-областей с помощью внесения локализованной случайной силы (форсинга) f i в уравнение импульса:

дрП і dt

+ дхі [pni _ к + pni п'_к + р + Tikj = pf i .

Поскольку в данной работе рассматриваются течения сжимаемого газа, в правую часть уравнения энергии будем включать работу этой силы pf i H i.

Форсинг f i может быть построен различными способами. В данной работе мы следуем идее из [10], где необходимость внесения f i в систему уравнений (1) обосновывается некоммутативностью гибридного фильтра и производной по пространству.

Рассмотрим аддитивную гибридную фильтрацию произвольной величины а [26]:

а = фа 11s + (1 - ф)(а), где ф — переходный параметр от RANS- к LES-области, aLES — LES-фильтрация, (а) — осреднение по Рейнольдсу. Если к отфильтрованной таким образом величине а применить производную по пространству, то получим да = да + ^1 / LES - ,п dxj   dxj   dx j

При выводе этой формулы предполагается, что некоммутативностью LES-фильтрации по сравнению с некоммутативностью гибридного фильтра можно пренебречь. Формула (3) показывает, что некоммутативность связана с пространственными градиентами переходного параметра ф В модели SST-IDDES роль ф выпо.тияет 1 — fa- Исходя из и того, сделаем f_i пропорциональным градиенту поля fa-

Основной эффект в (2), определяющий поле скорости, — это конвективный перенос импульса pU i U j = pU i U j + puiuj. Учтем в f i некоммутативность только этого слагаемого. Подставив в (3) а = pU i U j, мы обнаружим, что форсинг должен быть пропорционален

- // AES P i = p (VU U j )     —

(U i U j

Поскольку в гибридном расчете нам доступно лишь поле U i и его осреднение по времени, оценим p i как

P i та p(U i U j — (U i U j ) ) .

Перечисленные выше составляющие части форсинга следует дополнить случайным сомножителем, который обеспечит широкополосное наполнение вынуждающей силы f i. В данной работе предлагается использовать нормально распределенную случайную величину N с нулевым средним и дисперсией, равной 2тт. При таком подходе случайное поле не скоррелировано ни в пространстве, ни во времени.

Запишем итоговую формулу форсинга f i в виде

?, fi = С^дХГ. (UiUj — (UiUj)) N(0, 2тг), гДе Cfd — эмпирическая константа, которая была откалибрована в ходе расчета пограничного слоя на пластине и принята равной 0.32.

В качестве аппроксимации осреднения по Рейнольдсу в ходе расчета используется следующий алгоритм, применяемый на каждом шаге по времени:

^(аШ ⁺ A t ) = — • ^а(і ⁺ A t ) ⁺ ^1 —— ^ • (^a)^(t),

(a) (0) = а.

Здесь At — шаг по времени. Т = 10d_w/(U_t — u_w ) — характерное время осреднения. d_w — расстояние до ближайшей стенки, U_t — локальная скорость потока параллельно стенке, u_w — скорость стенки (в представленных далее тестах равна 0).

В дополнение к форсингу в данной работе используется еще одна модификация, предложенная впервые в [16]. В уравнениях для к и ш в RANS-области пограничного слоя используются осредненные по времени поля скорости вместо мгновенных. Это осреднение входит в конвективное слагаемое и в источник, отвечающий за производство. Осреднение выполняется согласно формуле (4). Стоит заметить, что улучшение профиля средней скорости и коэффициента трения можно получить и без дополнительного осреднения, как это было сделано во многих работах, где был использован какой-либо форсинг. В данной работе выбор в пользу дополнительного осреднения обусловлен двумя факторами. Во-первых, уравнения RANS-модели турбулентности откалиброваны по стационарным средним полям, и их применение в случае нестационарного течения может приводить к ошибкам [27]. Во-вторых, тестовые расчеты показывают, что осреднение позволяет снизить необходимую амплитуду форсинга втрое, что делает метод более устойчивым.

В следующих разделах рассматриваются результаты IDDES-расчетов пограничного слоя на плоской пластине и течения за закругленной ступенькой и анализируется влияние предложенных модификаций.

3.    Расчет пограничного слоя на плоской пластине с нулевым градиентом давления

В качестве первого тестового случая был выбран пограничный слой на плоской пластине с нулевым градиентом давления, так как именно в этом течении проблема LLM и заниженный коэффициент трения в рассматриваемой постановке наиболее выражены. В данной работе используются эталонные данные, которые находятся в открытом доступе [28].

Расчеты этого течения проводились в два этапа. На первом этапе выполнялся предварительный двумерный RANS-расчет, в котором пограничный слой нарастал от носика пластины. Из полученного решения выделялась подобласть, которая преобразовывалась в трехмерную, и использовалась для последующего IDDES-моделирования на втором этапе. В IDDES-расчетах входные профили параметров были взяты из предварительного RANS-расчета.

3.1.    Постановка задачи

Предварительный RANS-расчет был проведен в такой же постановке, как и в [28]. В нем рассчитывалась пластина длиной 2L, где L — 1 м, с буферной областью длиной 0.3 м перед ней. На входной границе задавался втекающий дозвуковой поток с числом Маха М — U^/c^ — 0.2, U^ — 68 м/с. Здесь с^ — V^к RT^ — скорость звука набегающего потока. Молекулярная вязкость рассчитывалась по формуле Сазерленда:

^ — ^^

T \^3/2

( Т^)

т^ + s т + s ’

гДе Дго — 1.667 • 10-5 кг/(м • с) подбиралось таким, чтобы число Рейнольдса Re — U^p^L/ц^ было равно 5 • 106. Остальные параметры в формуле Сазерленда были следующими: Т^ = 273 К, S = 122 К. Входные значения параметров турбулентности в предварительном RANS-расчете устанавливались равными к^ — 1.125— 1.06 • 10-3 f-V ,     ш^ — 125— 8655 с-1.

Re _l               \ с)                   L

На поверхности пластины к полагалось равным 0, а значение ш вычислялось по формуле ш_ш — 60ц/(0.075р(А51)²), где Аф — расстояние от центра пристенной ячейки до стенки. Пластина считалась теплоизолированной и на ней ставилось условие прилипания.

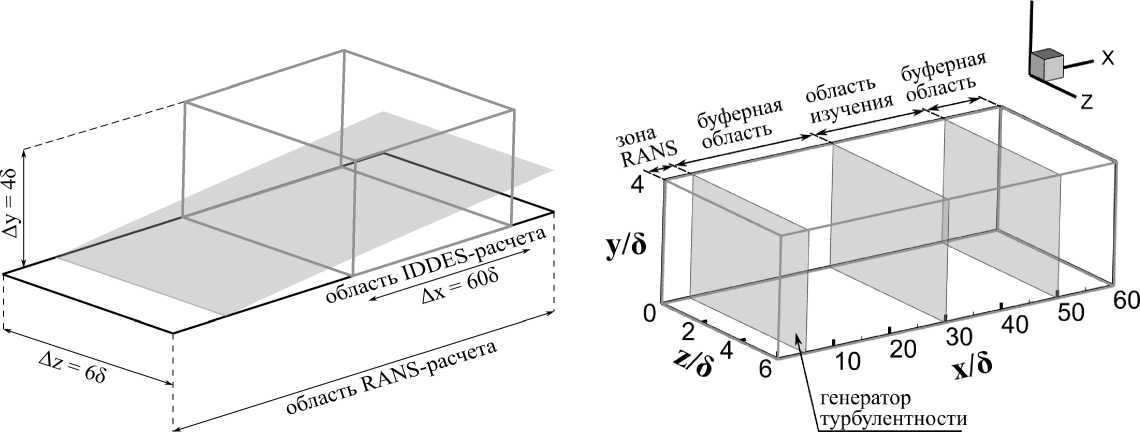
Расчетная область для IDDES-расчетов (рис. 1) представляла из себя участок пластины и имела размеры 605 х45 х65, где 5 — 0.0162 м — толщина пограничного слоя в контрольном сечении, определенная в предварительном RANS-расчете. На входной границе задавались параметры потока и турбулентности, получившиеся в этом сечении в ходе предварительного RANS-расчета всей пластины. Таким же образом были заданы параметры на верхней грани. Начальное поле также соответствовало RANS-решению. На боковых (вдоль направления у) границах расчетной области задавалось периодическое граничное условие, а на выходной границе ставилось условие свободного вытекания.

Как известно [1], метод IDDES требует внесения в расчетную область начальных нестационарных возмущений. В данной работе возмущения вносились генератором синтетической турбулентности [29], помещенным в сечение, находящееся на расстоянии 55 от входной границы. Он добавляет в решение случайные турбулентные пулвсации, которые генерируются по данным, взятвім из первого слоя ячеек после входного сечения. Таким образом, возмущения от генератора практически не доходят до входной границы, и пулвсации на каждом шаге по времени формируются по одним и тем же RANS-даннвім. Для статистического анализа результатов расчета использовался участок ж Е [305, 505], на котором турбулентности уже релаксировала к достоверной после генератора, а влиянием выходной границві еще можно пренебречь.

У

а)                                                    Ь)

Рис. 1. Расчетная область: а) соотношение с расчетом всей пластины в предварительном RANS, наклонная поверхность — граница пограничного слоя, Ь) общая структура

Используемая сетка имела постоянные шаги вдоль направлений ж и г, равные 5/10 и 5/16 соответственно. Эти шаги соответствуют рекомендациям авторов метода IDDES [1]. По направлению у сетка была сгущена к пластине, так что высота первой ячейки над стенкой равнялась вязкому масштабу длины пограничного слоя. На участке 0 <  у < 5, на котором находятся первые 58 ячеек, разбиение задавалось геометрическое, далее использовался постоянный шаг сетки по оси у, равный 5/10. Всего сетка содержала N_x xN_y х N_z = 600 х 88 х 96 - 5 • 10⁶ ячеек.

3.2.    Методы обработки

Для анализа статистических характеристик течения на представленных далее графиках результаты IDDES-расчета были осреднены по времени (решение осреднялось в течение промежутка времени 12 х 605/U^ г де 605 — длина расчетной области), а также по направлению г, вдоль которого течение статистически однородно. Локальный коэффициент трения Ср толщина потери импульса пограничного слоя Ө и соответствующее ей число Рейнольдса Re g вычислялись по следующим формулам:

рІОС _ ^Tw

С/ = 0.5ре и2’

_ f У™^; pU / гА           _ Ре Ue Ө

/0     Р е Ue (    Ue) ^У,              Р е ’

где T_w = p_w (dU/dy)_w — напряжение трения на пластине, у_тах ~ толщина пограничного слоя в данном сечении. Нижний индекс e обозначает значения величин на расстоянии у_тах от пластины, а индекс ш — значения величин на поверхности пластины.

Для построения профилей средней продольной скорости использовались переменные закона стенки ц+ у у +:

У

+ = У ІТ ’

І Т

^p w

V ^p w ^T w

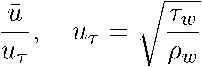
• 3.3.    Результаты

Мгновенные поля

Перед анализом осредненных по времени величин рассмотрим мгновенное поле течения в IDDES-расчете. На рис. 2 изображены изоповерхности Q-параметра:

_Q = ||Q||² — ||S||² = -1 Э^ д^

2            2 дх д дх і *

Видно, что области завихренности ( Q >  0) перемежаются с областями преимущественно безвихревых деформаций ( Q <  0), что согласуется с данными DNS канонических течений с развитой турбулентностью [30].

В IDDES-расчетах граница перехода решения из режима RANS в LES, соответствующая значению переходной функции /^ = 0.5, находилась на расстоянии около 0.15 от поверхности пластины для случая без форсинга и на расстоянии 0.35 для случая с форсингом. Это приемлемые значения для вихреразрешающего расчета пограничного слоя [1].

Рис. 2. Изоповерхности Q/max|Q| = +0.035 (светло-серый), Q/max|Q| = -0.035 (темно-серый), где max|Q| — максимальная абсолютная величина Q в расчетной области

Статистическая обработка

На рис. 3-4 представлены результаты обработки результатов, осредненных по времени и по направлению г. На рис. 3 показано сравнение распределения Re e вдоль пластины и зависимости 6^^с (Re_e ), полученных в RANS- и IDDES-расчетах, также приведена эмпирическая зависимость C^j (Re_e) [31]. Можно видеть, что в IDDES-расчете без форсинга значения Re e получаются заниженными вплоть до 3% относительно RANS-расчета. График 6^^с на участке 6600 <  Re e <  8500 ведет себя качественно неправильно, что вызвано перестроением возмущений от генератора турбулентности к развитым турбулентным пульсациям. Эта перестроение происходит в буферном участке 255 и не влияет на область изучения 305 < х < 505. В области Re e >  8500 значения коэффициента трения для расчета без форсинга занижены на 4 — 6% по сравнению с RANS-решением. Внесение форсинга позволяет получить близкие к RANS значения С^у^с и немного уменьшить буферную зону после генератора турбулентности.

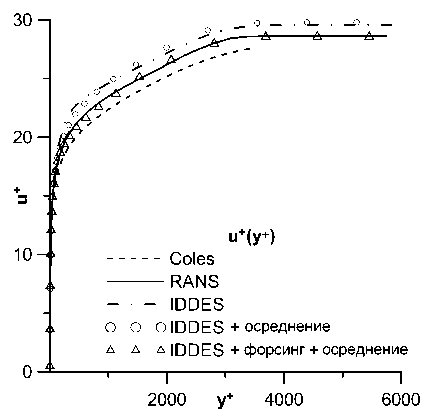
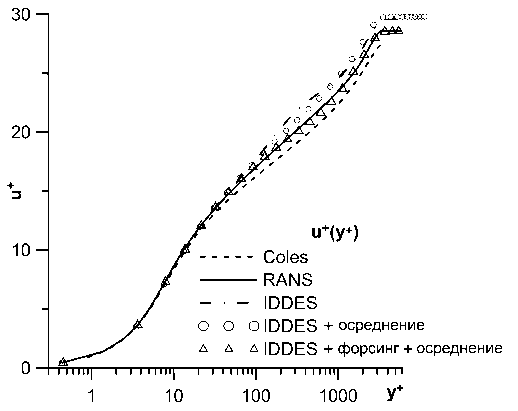
На рис. 4 показаны полученные профили скорости пограничного слоя в линейном и логарифмическом масштабах в контрольном сечении Ree = 10 000. Также приведен эталонный профиль скорости [32]. Граница RANS- и LES-областей находится на логарифмическом участке пограничного слоя при у+ ~ 450 для расчета без форсинга и при у+ ~ 1300 для расчета с форсингом. Можно заметить, что в первом случае в переходной области логарифмического участка ярко выражен сдвиг графика. Дополнительное осреднение в уравнениях для параметров турбулентности к и ш позволяет устранить перегиб на логарифмическом участке, но при этом остается неправильным наклон графика. Добавление случайных возмущений позволяет полностью устранить проблему Log-Layer Mismatch.

4.    Расчет течения за закругленной ступенькой

В качестве второго тестового случая для нового метода форсинга был выбран расчет дозвукового течения за закругленной ступенькой в плоском канале. Данные эталонного LES-расчета с разрешением вплоть до стенки (WRLES — Wall-Resolved Large Eddy Simulation) [35] находятся в открытом доступе [33]. Помимо этого, существует эксперимент [34] по этому же течению.

Проблема LLM слабо заметна в течениях с отрывом (и в целом в неустойчивых течениях с перегибом среднего профиля скорости) [13]. Таким образом, для данного случая основным требованием к форсингу было то, что он не должен искажать исходное IDDES-решение. Дополнительным требованием было отсутствие неустойчивости метода в окрестности закругленных поверхностей, наблюдавшейся в некоторых предыдущих работах [13].

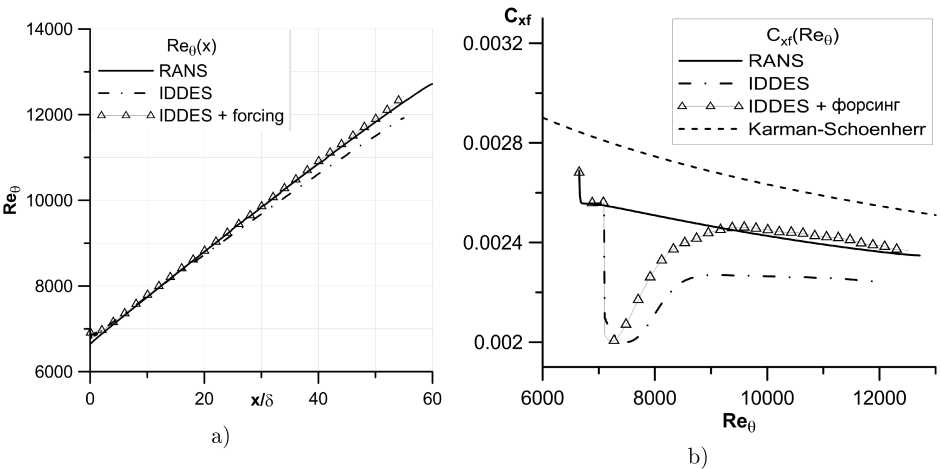
Рис. 3. Сравнение решений, полученных в RANS- и IDDES-расчетах: a) Re_g (ж), b) Cj (Reg )

4.1.    Постановка задачи

Исследуется обтекание дозвуковым потоком газа гладкой обратной ступеньки в канале. Левая граница расчетной области расположена в сечении ж = —7.339Н, где Н — высота ступеньки, правая — при ж = 15.47Н. Высота кан ала на входе 8.524Н, координата начала ступеньки ж = 0. Число Рейнольдса Re, вычисленное по высоте ступеньки, составляет

Re = PmU™^H = ізб₀₀.

Ц

Индексом «іп» обозначены параметры ядра набегающего потока, коэффициент молекулярной вязкости ц полагался постоянным по пространству и не зависел от температуры. Была выбрана слабосжимаемая постановка при числе Маха М = Um/c^ ~ 0.2 с параметрами:

U_in = 70 р _йп = 105 096 Пa, p_in = 1.2 ^3, Н = 0.0137 м, ц = 8.4 • 10^-5^.  (7)

а)

Рис. 4. Профиль осредненной продольной скорости и + (у +): а) в линейном масштабе, Ь) в логарифмическом масштабе

Ь)

Используемая сетка была основана на сетке, опубликованной на сайте [33]. Распределение узлов по направлению оси ж было сохранено, как и распределение узлов по оси у в нижней половине канала. В верхней половине распределение узлов по оси у было заменено на совместимое с граничным условием прилипания потока. Вдоль направления оси д расчетная облаеть имела ширину 3.17 Н и была равномерно разбита на 192 ячейки. После этого полученная сетка была прорежена в 2 раза по всем направлениям и итоговое количество ячеек составило N_x х N_y х N_z = 384 х 126 х 96 ~ 4.6 • 106 ячеек. При этом характерный размер ячейки в области отрыва был равен Дье s = 5 • 10^-4 м. На боковых поверхностях ставилось условие периодичности в направлении оси д. Общий вид сетки сбоку показан на рис. 5, вид в перспективе (в том числе разбиение на блоки) - на рис. 6.

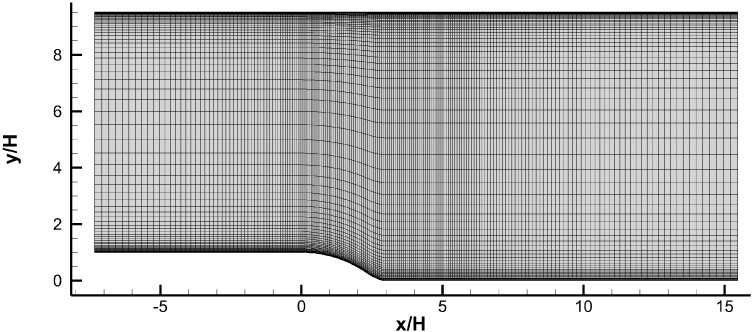
Рис. 5. Общий вид расчетной сетки в плоскости ж — у для IDDES-расчетов задачи течения за закругленной ступенькой. Показан каждый второй узел вдоль сеточных направлений

На стенках канала задавалось адиабатическое условие прилипания, на выходе - постоянное статическое давление. На входе задавались профили параметров, полученные заранее в предварительном RANS-расчете «подводного канала». Подводной канал постоянного сечения имел такое же распределение узлов в поперечном направлении, что и вход в основной канал. В продольном направлении были расположены 4 ячейки одинакового размера, причем вход и выход канала были связаны периодическим граничным условием. В канале продольная скорость и давление брались из осредненных эталонных данных WRLES и не менялись в процессе расчета. На фоне такого «замороженного» поля течения велось установление параметров турбулентности к и ш. Этот расчет проводился по схеме WENO5 с оптимальными весами [36] методом установления по неявной схеме с первым порядком точности по времени. В основном расчете, как и в предыдущем тесте, для перевода решения в вихреразрешающий режим использовался генератор синтетической турбулентности [29], расположенный на расстоянии Н от входной границы.

Рис. 6. Общий вид расчетной области для IDDES-расчетов задачи течения за закругленной ступенькой и блочная структура сетки

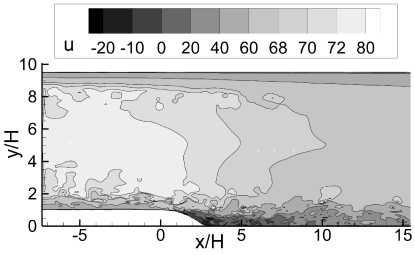
Качественная картина мгновенного поля течения приведена на рис. 7. Хорошо видно место установки генератора турбулентности. Верхний пограничный слой был оставлен в близком к RANS режиме, так как подробности описания турбулентности в этой области не представляли интереса, а влияние пограничного слоя сводилось к его вытесняющей способности.

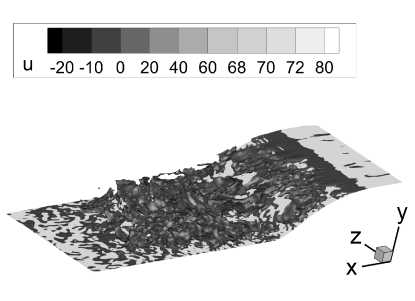
Рис. 7. Качественная картина мгновенного поля течения: а) изоповерхности и = 0, Ь) поле продольной скорости

а)

Ь)

4.2.    Результаты

В расчете осреднение параметров потока проводилось за время 0.2 с. Этот промежуток соответствует примерно 45 характерным временам, где характерное время соответствует времени прохода невозмущенного потока газа через расчетную область. Для анализа статистических характеристик данные были дополнительно осреднены по направлению г. Координаты точек отрыва и присоединения определялись по этим осредненным данным.

Размер отрыва

IDDES-расчеты и с форсингом, и без него показывают примерно одинаковые средние координаты точки присоединения: х/Н = 5.23. В эталонном LES-расчете [35] эта координата равнялась 4.35, в эксперименте [34] — 4.21. Отличие наблюдается в координатах точки отрыва: в расчете с форсингом х/Н = 0.69, в базовом IDDES-расчете — 0.66. В обоих случаях длина отрыва завышена, и форсинг лишь незначительно приближает ее к эталонному значению.

Профили осредненных характеристик

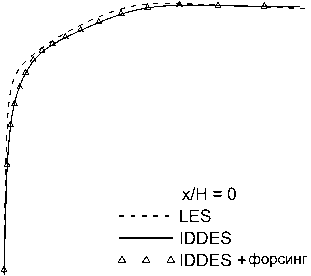
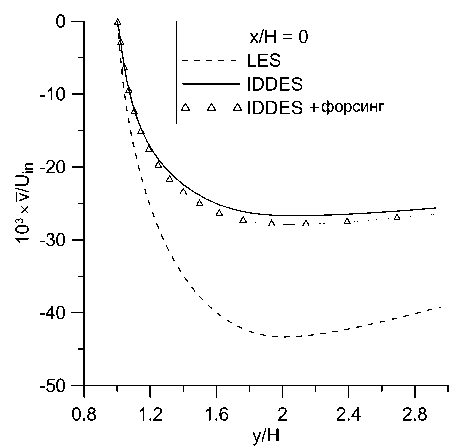
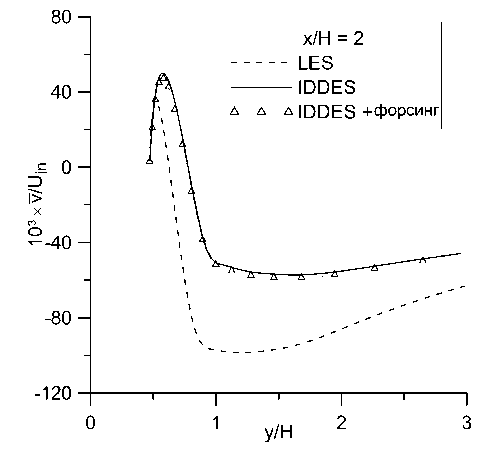
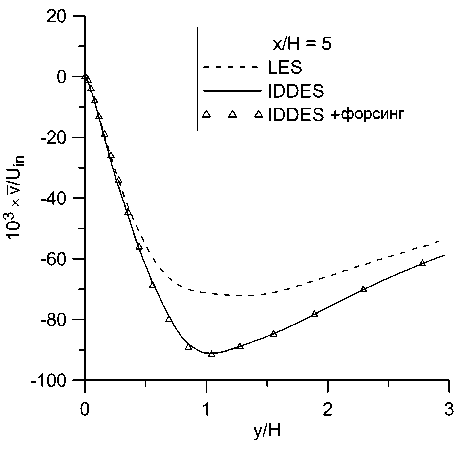
Было проведено сравнение профилей средних продольной и поперечной компонент скорости, а также напряжений Рейнольдса и‘ г‘ в контрольных сечениях с относительной координатой х/Н = 0, 2, 5,10.49. Полученные результаты представлены на рис. 8-10.

60 о

0.8     1.2     1.6      2      2.4     2.8

У/Н                     а)

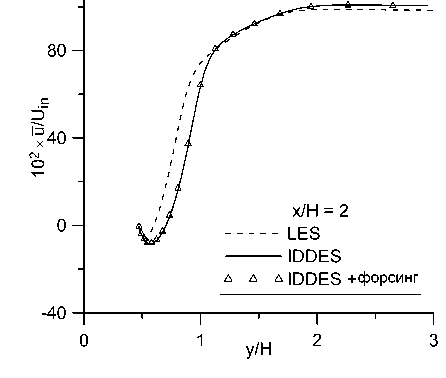
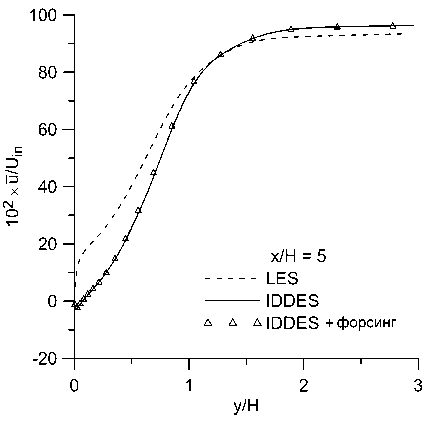
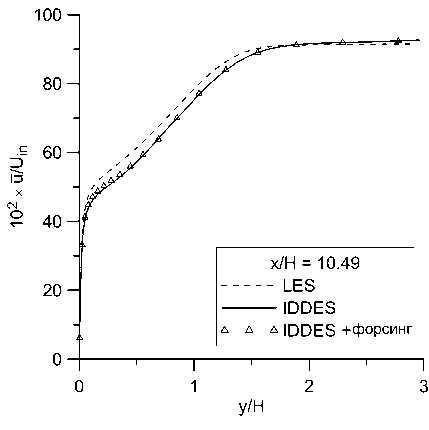
Рис. 8. Профили осредненной продольной компоненты скорости и в сечениях: а) х/Н = 0, Ь) х/Н = 2, с) х/Н = 5, d) х/Н = 10.49

d)

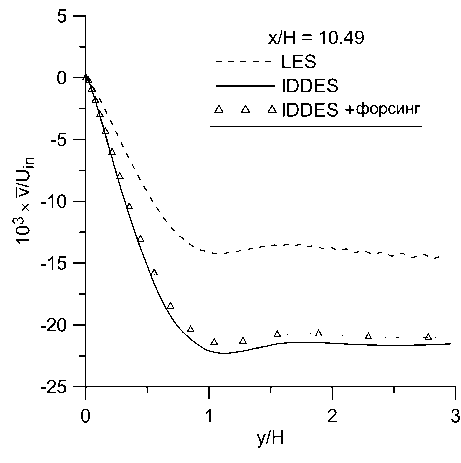
Видно, что во всех сечениях полученные профили продольной скорости практически одинаковы в расчетах с форсингом и без него и отличаются от эталонного решения почти везде менее, чем на 10%. В профилях поперечной скорости и напряжений Рейнольдса отличия более заметны, но они также относительно небольшие. Малость отличий между расчетами с форсингом и без него согласуется с наблюдениями, сделанными в работе [13]. Помимо влияния неустойчивости течения, этот эффект может быть обусловлен тем, что в данном расчете генератор турбулентности находится близко к изучаемой области. Он генерирует возмущения по эталонным данным WRLES, что минимизирует проблему LLM и заниженное трение в своей окрестности. Отсутствие отличий между двумя проведенными расчетами можно считать положительным результатом, так как форсинг не должен искажать решение, в котором проблема LLM не проявляется.

Ь)

с)

d)

Рис. 9. Профили осредненной поперечной компоненты скорости v в сечениях: а) х/Н = 0, Ь)

х/Н = 2, с) х/Н = 5, d) х/Н = 10.49

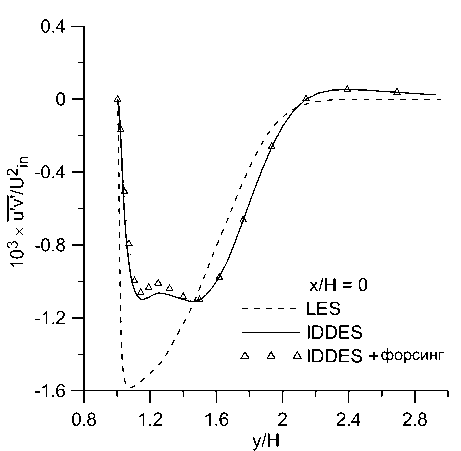
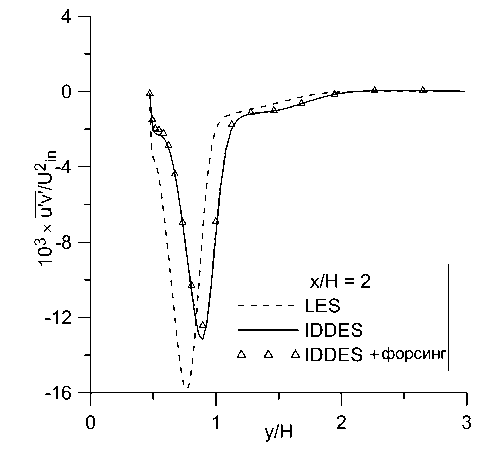
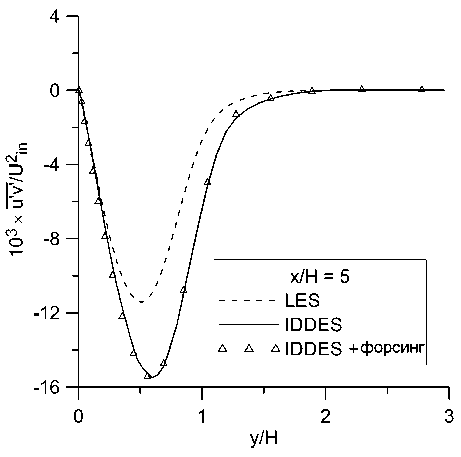
с)

Рис. 10. Профили напряжений Рейнольдса п‘ и ‘ в сечениях: а) х/Н = 0, b) х/Н = 2, с) х/Н = 5, d) х/Н = 10.49

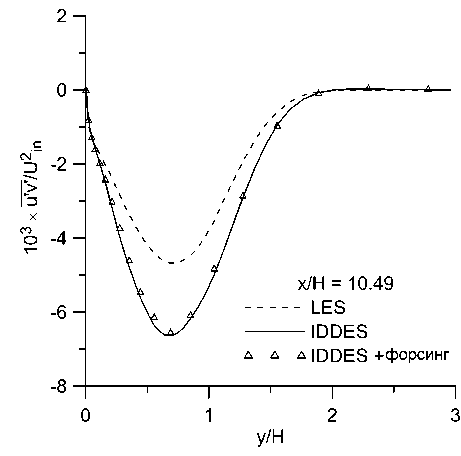
d)

5.    Заключение

Предложен метод учета взаимодействия RANS- и LES-областей в гибридных расчетах. Для случая пограничного слоя на плоской пластине с нулевым градиентом давления получено улучшенное распределение трения по сравнению с базовым IDDES-расчетом, а также устранен сдвиг логарифмического участка в профиле средней скорости. На течение за закругленной ступенькой метод оказывает слабое влияние, что, вероятно, связано с близким расположением генератора синтетической турбулентности к исследуемой области, а также с тем, что это течение достаточно неустойчиво, чтобы хорошо описываться базовым методом IDDES.

В отличие от предыдущих разработанных методов, новый метод взаимодействия использует лишь локальные по пространству данные (вследствие чего совместим с параллельными расчетами), что обеспечивает его применимость к расчетам задач с произволь- ной геометрией границ. Метод основан на идее некоммутативности гибридного фильтра и производной по пространству, которая применима ко всем гибридным методам. Проверено, что метод остается устойчивым как в расчете пограничного слоя на плоской пластине, так и в течении за закругленной ступенькой.

Исследование выполнено за счет гранта Российского научного фонда № 21-71-10105,