Подходы к описанию пространственной динамики миграционно-связанных популяций: анализ синхронизации циклов
Автор: Кулаков М.П., Аксенович Т.И., Фрисман Е.Я.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Математическое моделирование
Статья в выпуске: 1 т.16, 2013 года.
Бесплатный доступ
В работе рассматривается два подхода для описания пространственной динамики миграционно-связанных популяций: на основе систем связанных обыкновенных дифференциальных уравнений и систем связанных логистических отображений. Показано, что в первом случае пространственная динамика носит достаточно монотонный характер - стремление к единственной нетривиальной стационарной точке. Во втором - динамика оказывается намного сложнее и может иметь периодический и нерегулярный режимы, а колебания численности могут носить как синхронный, так и несинхронный характер.
Пространственно-временная динамика, метапопуляция, миграция, системы связанных обыкновенных дифференциальных уравнений, системы глобально связанных отображений, синхронизация
Короткий адрес: https://sciup.org/14328824
IDR: 14328824 | УДК: 530.182:574.34
Текст научной статьи Подходы к описанию пространственной динамики миграционно-связанных популяций: анализ синхронизации циклов
Для большинства видов животных характерно неравномерное распределение особей по ареалу. Часто это связано с тем, что на рассматриваемой части ареала имеется несколько мест обитания данного вида, между которыми существует постоянное или переменное сезонное миграционное взаимодействие. Систему локальных популяций, связанных миграцией, принято называть метапопуляцией [13]. При этом механизмы формирования нерегулярного и периодического поведения всей метапопуляции оказываются существенно сложнее, чем отдельной изолированной популяции, и в большей степени определяются географической структурой ареала и миграционными взаимодействиями [8, 9, 13].
Для количественного описания динамики миграционно связанных популяций обычно используются системы связанных логистических отображений [1,3-7, И] или системы связанных обыкновенных дифференциальных уравнений [7, 9, 12]. В обоих этих подходах динамика каждой локальной популяции, являющейся частями более крупной метапопуляции, описывается одиночными уравнениями с плотностно-зависимым регулированием роста численности. Связь между отдельными популяциями описывается в виде соответствующей аддитивной или мультипликативной добавки к моментальным плотностям, определяемой миграционными перемещениями из одного локального участка в другой. Подобные системы, будучи хорошо изучены, обладают богатой феноменологией: здесь выявлены эффекты мультистабильности, синхронизации, хаоса, перемежаемости и др. [1, 3-7, 11]. При изучении систем связанных отображений весьма важным является вопрос обнаружения и изучения механизмов синхронизации подобных систем, которая в биологической трактовке может быть использована для количественной идентификации связанных популяций. Так, две слабо связанные популяции, динамика которых демонстрирует синфазное поведение, могут быть приняты за одну, в то время как небольшое изменение параметров связи может привести к возникновению противофазных колебаний и выявить принципиальное различие в динамическом поведении популяций, не отражаясь при этом на динамике их суммарной численности.
Целью данной работы является математическое моделирование пространственно-временной динамики популяций животных. В ней рассматривается два упомянутых подхода к моделированию пространственной динамики метапопуляций: модель с непрерывным и дискретным временем. Исследуется простейший случаи, когда пространственно распределенная популяция представлена системой двух взаимодействующих локальных групп особей, связанных между собой миграцией. Исследование данных математических моделей проведено численными и аналитическими методами, включая исследование на устойчивость, построение фазовых и параметрических портретов, исследование характера возможных бифуркаций, построение бассейнов аттракторов и областей синхронизации.
Модель динамики численности двух миграционносвязанных популяций с непрерывным временем
Допустим, что на некоторой территории существует два относительно изолированных местообитания, в каждом из которых обитает локальная популяция (субпопуляция), связь между ними выражается лишь в их миграционном взаимодействии. В качестве этих субпопуляций можно принимать какие-либо обособленные группы особей, например, стада копытных, совершающих сезонные миграции, либо примыкающие друг к другу учетные территории [8,13]. Предположим, что особи, обитающие на этих территориях, изолированы от других и связаны между собой лишь миграциями. В этом случае ареал может быть схематично изображен в линейном виде, показанном на рис. 1, где первая популяция, имеющая в какой-то момент времени численность х, миграци-онно-связана со второй с численностью равной у. Стрелки на рис. 1 указывают направления перемещения особей, а коэффициенты тх - доля особей, перемещающихся из 2-й субпопуляции в 1 -ю, а т2 - перемещающихся из 1 -й во 2-ю. Интенсивность таких миграций определяется численностью мигрирующего вида той субпопуляции, откуда и куца происходит миграция.
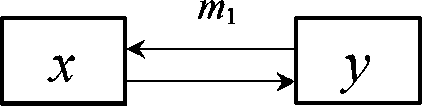
W2
Рис 1. Система двух миграционно-связанных популяций
В случае полной изолированности этих двух местообитаний ктх = т2 = 0) динамику численности каждой такой субпопуляции можно описать достаточно простыми уравнениями логистического роста вида:
. dx dy х = — = ггх - Sxx и у = --= г2у - з2у dt dt ' '
где г - максимальная скорость роста популяции, s - параметр, определяющий интенсивность плотностного регулированная роста численности, который вместе с параметром г определяет экологическую нишу данного местообитания равную г]s . Ограничимся в дальнейшем случаем полной идентичности субпопуляций и симметричным характером миграционного взаимодействия, те.
гх - гг = г, sx = sг = s и тг = т2 - т.
При непрерывном процессе воспроизводства миграция между отдельными субпопуляциями в метапопуляции может также носить непрерывный характер, те. происходить постоянно и одновременно с процессами размножения. Если при этом эмигранты неотличимы от местных особей и наравне с местными особями участвуют в воспроизводстве, то пространственную динамику такой метапопуляции можно описать системой уравнений вида:
х = гх - sx 2 - тх + ту у = ry - sy 2 - ту + тх '
Рассмотрим особенности динамических режимов и бифуркации системы (1). Для большей наглядности и простоты будем в дальнейшем рассматривать безразмерный аналог системы (1):
^х=гх(1-х')-тх + ту
[ у = гу (1 - у) - ту + тх ’ ^ которую легко получить из (1) заменой ^х ^ х и S
-у -> У-г
Стационарные точки системы (2) можно получить как пересечение ее нуль-изоклин:
у = — (та 2 + кт - г)х) т х = — (г 2 .у + кт - г)^)’ т
Решением системы (3) всегда будут тривиальная (0;0) и нетривиальная (1; 1) стационарные точки системы (2), которые соответствуют стационарным точкам одиночных уравнений (при ^=0). При пересечении границы области, определяемой неравенством 12m] < г, тривиальное равновесие испытывает бифуркацию трезубца [2] и в системе (2) появляется пара стационарных состояний, соответствующих корням системы (3) с отрицательными координатами, не имеющие биологически значимого смысла. При этом надо отметить, что, несмотря на наличие двух этих точек, траектории системы (2), при положительных начальных условиях, целиком лежит в положительном квадранте, другими словами, он являет притягивающим множеством.
Для определения областей устойчивости всех полученных стационарных состояний легко вычислить собственные числа якобиана систем (2) в каждом решении системы (3). На рис. 2 показаны области устойчивости, полученные методикой, предложенной в [6, 10]. Расчет производился только для биологически значимых параметров, те. при г > 0 и 0 < m< 1. Линии ^ = 2m и Г =0 соответствуют бифуркационным линиям смены типа устойчивости стационарных состояний, а первая и бифуркации трезубца [2].
Область устойчивости нетривиальной стационарной точки, соответствующая устойчивому узлу, обозначена на рис. 2 а буквами А и В и представляет собой положительную часть параметрической плоскости. В первой области система (3) имеет 4 решения (рис. 2 б) и при пересечении параметров линии г = 2m в системе (2) происходит слияние трех седловых стационарных состояний в одно тривиальное равновесие - неустойчивый узел (рис. 2 в). В области В параболы (3), как показано на рис. 2 в, пересекаются только в двух точках, одна из которых нетривиальная - устойчивый узел, а другая тривиальная - седло.
Исследование качественных особенностей динамических режимов модели (2) показывает, что метапопуляции, состоящие из двух идентичных симметрично свя-
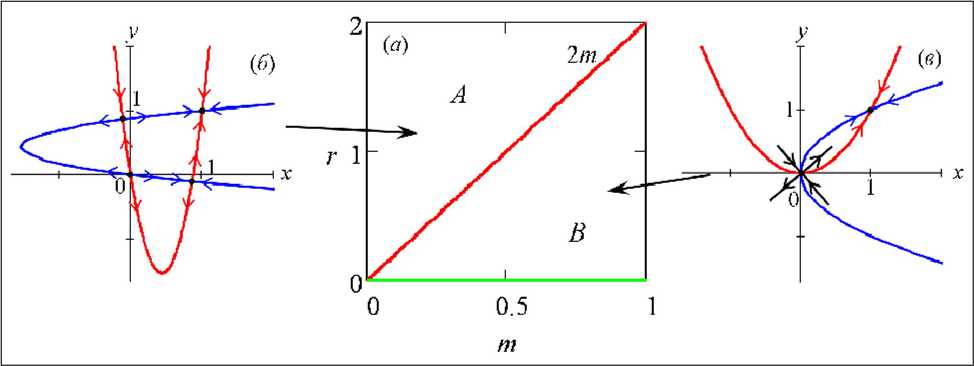
Рис. 2. (а) Область устойчивости нетривиальной стационарной точки системы (2), (б)-(д) нуль изоклины (3). Стрелки указывают на тип устойчивости стационарных состояний
занных популяции с непрерывным процессом воспроизводства, характеризуются наличием единственного устойчивого стационарного состояния в области допустимых значений популяционных и миграционных параметров. В этом случае, при положительных значениях параметров, наблюдаются достаточно монотонные режимы динамики - стремление к нетривиальной стационарной точке.
В случаях, когда миграция имеет непостоянный характер, например переменный или сезонный, для описания пространственной динамики таких метапопуляций потребуется использовать системы неавтономных дифференциальных уравнений. Если же эмигранты после переселения начинают участвовать в воспроизводстве с некоторой задержкой, потребуются системы уравнений с запаздыванием либо уравнения второго и более порядка. В случаях, когда наряду с миграцией и воспроизводство имеет сезонный характер, для описания пространственной динамики логично воспользоваться системами рекуррентных или дискретных уравнений.
Дискретная модель динамики численности двух связанных популяций
Рассмотрим популяцию, особи которой имеют явный стадийный характер развития и динамика которой может быть описана моделями с дискретным временем. Пусть такая популяция состоит из двух локальных групп особей, связанных между собой сезонными миграциями. Предположим, что значимыми для развития популяции являются процессы размножения и гибели, тогда можно утверждать, что расселение (миграция) возможно либо до периода размножения, либо после него. При этом миграционная связь между локальными популяциями может происходить двумя различными способами (рис. 3).
Первый из них состоит в том, что особи мигрируют в промежутках между сезонами размножения, как показано на рис. 3 а. Эмигранты при этом ничем не отличаются от местных особей и сразу начинают участвовать в процессах размножения, независимо от того, как происходило расселение: до периода размножения либо после него. Далее будет показана полная эквивалентность таких случаев. Подобный вид связи принято называть диссипативной, и она, очевидно, способствует выравниванию мгновенных численностей [3].
Второй способ миграции состоит в том, что особи мигрируют из одной локальной популяции в другую в обход процессам размножения и гибели, как показано на рис. 3 б. Эмигранты в этом случае становятся неотличимы от местных особей и начинают участвовать в размножении лишь через сезон. Подобный вид связи характерен для популяций, в которых в размножении участвуют лишь наиболее оседлая часть особей, а наиболее подвижная их часть, например молодняк, после переселения на другую территорию начинает участвовать в размножении только в следующем сезоне. В этом случае миграция также может происходить в начале сезона до размножения или после. Такой способ связи принято называть инерциальным, и миграция в этом случае не будет сглаживать мгновенные численности, а порой будет становиться причиной флуктуаций численностей [3].
Эти два способа миграции в общем схожи с приведенным в предыдущем разделе описанием модельной динамики миграционо-связанных популяций с непрерывным временем, однако уравнения динамики популяций с дискретным временем не в полной мере являются просто дискретным аналогами уравнений (1) и (2). Перейдем к описанию уравнений динамики популяций с дискретным временем.
Обозначим численность первой популяции в начале и-го сезона размножения через xr, а второй соответственно уп. Пусть процессы локального воспроизводства (рождаемости и гибели) в случае отсутствия миграционной связи описываются дискретными аналогами уравнения
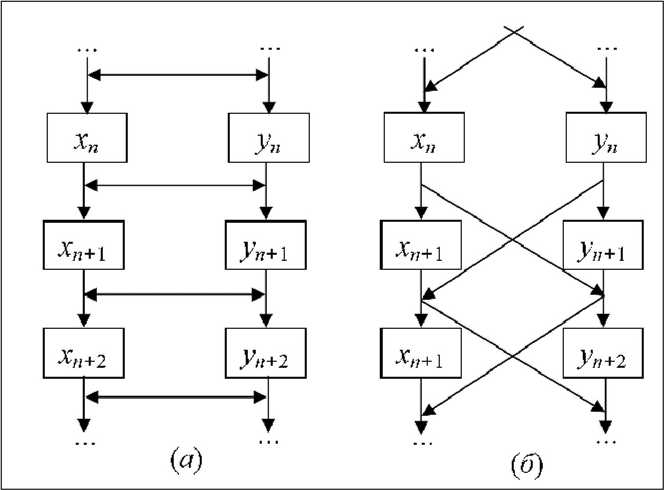
Рис 3. Система двух миграционно-связанных популяций с (а) диссипативной и (б) инерциальной связью
Ферхюльста: х„и = ахп (1 - кх J и уи+1 =^(1-^), где параметр а - максимальная скорость роста популяции (репродуктивный потенциал), к - параметр, определяющий интенсивность плотностного регулирования роста численности, \]к - емкость экологической ниши. Как и ранее, ограничимся случаем полной идентичности локальных популяций и равенством миграционных параметров. Будем также рассматривать модели с безразмерными численностями, те. полученными при замене переменных в уравнении Ферхюльста: кхп —>хп и ку. ~*Уп-
В случае, если миграция происходит после процессов локального воспроизводства (рис. 3 а), уравнения динамики численности представляют систему отображений вида:
fx„ + i = ах „ (1 - х„ X1 - т) + ату „ (1 - у„ ) ^ t^^i = «у Л1 - у Л1 - ”0+ ^ Л1 - ^ У 1
Если миграция предшествует воспроизводству, уравнения динамики можно записать системой вида:
х„ + 1 = а(х» (1 - ”0 + ту„ Х1 - х„ (1 - щ) - ту и)
У„ + 1 = ^Х1 - ™) + ^Л1 - У» О - т)- тх„)’ которая при замене переменных Хп (1 — w) + туп ~>Хп и уу(1-т) + тз^ ~>уп оказывается эквивалентным системе (4).
Если популяции связаны вторым способом (рис. 3 б) и миграция предшествует процессам воспроизводства, динамику численности можно описать системой отображений вида:
,X + i = ахУ-тУ-xnt\-т$)А-туп + 1 = фЛ " "1X1 " У „О " “))+ тс. ’ которая с заменой ^(1-т)2 -»х„ и ^„(1 — т'У —>уп значительно упрощается:
X+i = ах„ (1 - х„ ) - атх„ + ту„ 7„+i = аУ« (! - У J - атУ« + тх» '
Динамические режимы модели с инерциальной связью
Начнем изучение динамических режимов моделей миграционо-связанных популяций с дискретным временем с рассмотрения системы (5).
Как и система (2), система (5) имеет от 2 до 4 неподвижных точек: тривиальную х = у = 0 и нетривиальную х - у - (1 - т)-—-, а также пару корней с отрицатель-а
1 + т ными координатами, которые существуют при а >----
1 — т
1 - 3m и у < ------• Выход из этих областей сопровождается бифуркацией слияния этих точек с тривиальным равновесием, что показано на рис. 4 б-д. При биологически значимых значениях параметров (я>0 и 0 < т < 1) устойчивыми могут быть лишь тривиальная при ^ < 1 1ШИ нетривиальная неподвижная точка при 1 < я < 3. На рис. 4 а показаны эти области, где цифрой 1 отмечена область устойчивости нетривиальной стационарной точки, цифрой 0 - тривиальной.
Как известно [1,5,11], системы отображений подобного вида характеризуются мультистабильным характером возможных динамических режимов, те. в зависимости от начальной точки итерирования возможно формирование принципиально разных аттракторов (циклов разной степени синхронизации и циклов разной длины). Для исследования данного феномена и определения областей существования синфазных и несинфазных цик-
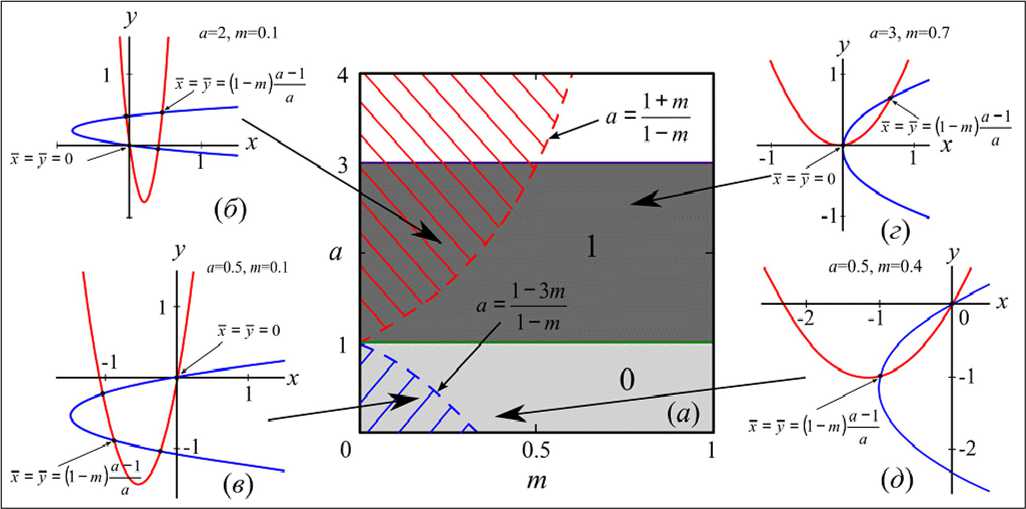
Рис 4. (а) Область устойчивости тривиального и нетривиального равновесия системы (5) и (б)-(д) их эволюция
лов системы (4) и (5) воспользуемся методикой построения бассейнов притяжения, а также известной техникой построения карт динамических режимов.
Ранее в [8] для количественной идентификации достигаемых режимов синхронизации систем вида (4) был предложен следующий количественный показатель:
xi ~ Z
1 Л
^ =Тт—L N и i = n
где XJ и у t (z = ОД.. ^N) - N итераций системы (4) или
(5), из которых вычисление величины К х производится лишь для последних N-n итераций, взятых на аттракторе. Несложно заметить, что величина Кх равна нулю при полной синхронизации динамик переменных х и у; отлична для асинхронных режимов и режимов полной противофазной синхронизации; близка к нулю в случаях частичной синхронизации. Более того, у двух разных аттракторов с разной степенью синхронизации значения этой величины будут различны. Надо отметить, что величина Кх позволяет хорошо идентифицировать синхронизацию колебаний лишь для наборов Xt и у t достаточно близких по своим абсолютным значениям, что, очевидно, характерно для систем отображений (4) и (5), так как они переводят единичный квадрат в себя.
Вариации величины Кх в зависимости от начальной точки итерирования XQ , у0 и управляющих парамет ров позволяет произвести качественную идентификацию на фазовой плоскости областей, соответствующих различным начальным условиям систем (4) и(5), приводящих к конкретному режиму синхронизации, те. позволяет построить бассейны притяжения, приведенные ниже. На рис. 5 в—2 и б б-u приведены построенные по данной методике бассейны притяжения, где различными оттенками серого показаны области, соответствующие различным значениям величины К х . Для большей информативности цифрами на них также указаны длины циклов, возникающие в системе (4) и (5) при начальных условиях, взятых из данного бассейна притяжений.
Нижний индекс 0 у длин циклов на первой карте (рис. 5 а) показывает формирование синфазных циклов, без индекса - несинфазных (рис. 5 б). Буква Q на рис. 5 б - область квазипериодической динамики, С - хаотическая динамика, а на рис. 5 а С - нерегулярная динамика (без разделения на хаотическую и квазипериодическую). Цифры на отдельных частях бассейнов притяжения одного цвета показывают, к какому конкретно аттрактору относится данный бассейн.
Анализ полученных карт и бассейнов притяжения показывает, что первая бифуркация нетривиальной особой точки - рождение полностью противофазного цикла длины 2, а дальнейшие бифуркации приводят лишь к дроблению бассейна несинфазных циклов. На рис. 5 а буквой N отмечена область, в которой синфазные циклы не существуют либо неустойчивы и не наблюдаются в системе (5) при любом начальном состоянии системы. Это подтверждается бассейном притяжения, показанным на рис. 5 в белым цветом, целиком заполняющим допу-
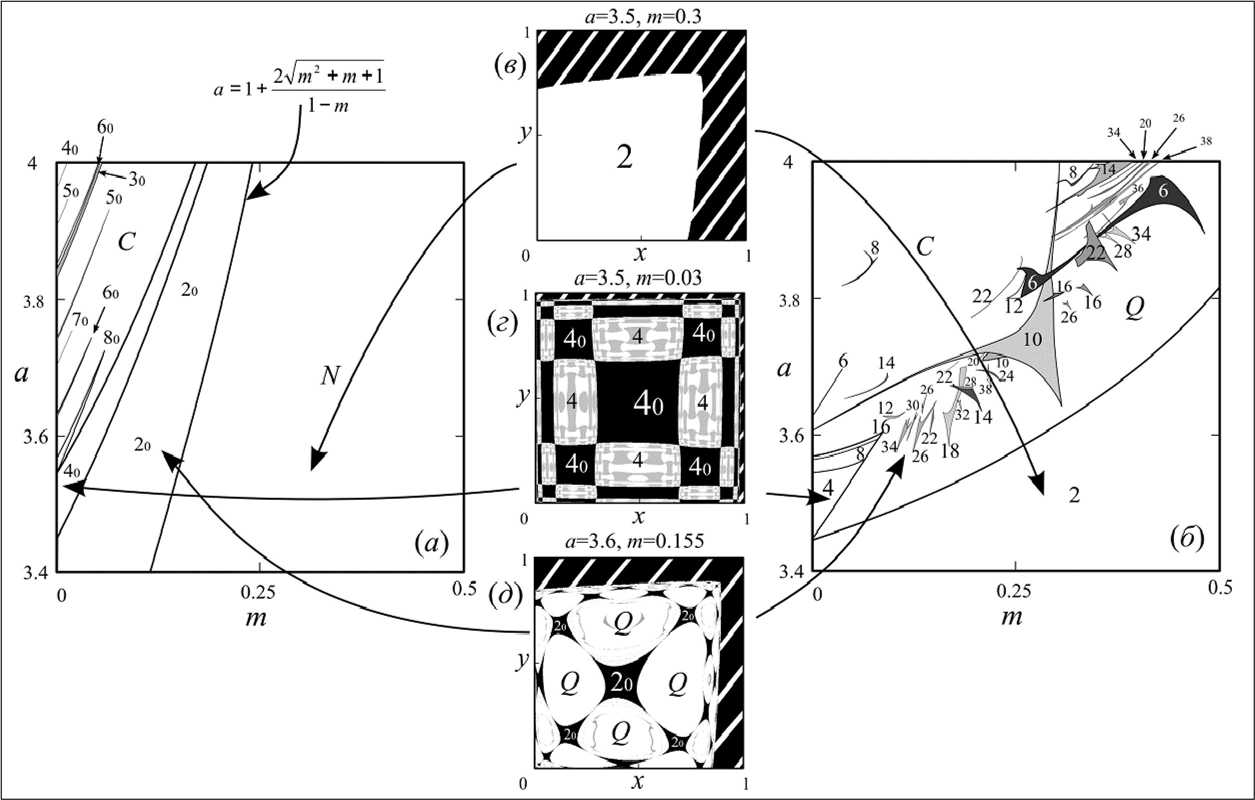
Рис. 5. Карта динамических режимов (а) синфазных и (б) несинфазных режимов системы (5), (в)-(д) бассейны притяжений
стимую часть фазового пространства, в которой Кх = const > 0. Область, отмеченная штриховкой, - это область, в которой система (5) теряет смысл (образ точек из этой части фазовой плоскости не лежит в единичном квадрате, на котором определено единичное уравнение Ферхюлста).
После первой бифуркации нетривиальной неподвижной точки (при а > 3) в системе формируются преимущественно несинфазные циклы длины 2. Исключением является область параметрической плоскости, полученная пересечением областей, показанных цифрами 2 и 20 на рис. 5 а и б, в которой возможно одновременное формирование как синфазного, так и противофазного цикла длины 2, в зависимости от начальной точ-
2^т 2 + m + 1 ки итерирования х и у При а < 1 + ------------ 1 - т синфазные 2-циклы, как и любые другие синфазные режимы, не существуют либо неустойчивы.
На рис. 5 г показаны бассейны притяжения синфазных и несинфазных циклов длины 4. Для последних воз можно три различные фазы, значения величины К х для которых будут немного различны, что выражается в том, что бассейн притяжения несинхронного 4-цикла на рис. 5 г имеет раздробленный вид. На рис. 5 д приведены бассейны притяжения принципиально разных режимов - синфазных циклов длины 2 и предельных циклов, соответствующих несинфазным циклам, обозначенные соответственно как 20 и Q.
Динамические режимы модели с диссипативной связью
Рассмотрим особенности динамических режимов системы (4), описывающей пространственную динамику двух миграционно-связанных популяций в случае, когда эмигранты неотличимы от местных особей. Как и одиночное уравнение Ферхюльста, система (4) имеет а- 1 тривиальную Хо у0 = 0 и нетривиальную *, = у, =--- особую точку. Аналогично системам (2) и (5) система (4) может иметь еще пару особых точек (xjpjjJ и (•^io’^io^ которые существуют при я > ^ и
1 - 4m а >--------.
1 - 2m
Если в первой из этих областей они содержат отрицательные координаты, не имеют биологически значимого смысла и неустойчивы, то во второй области, которая существует в случае сильной миграционной свя-
2^т2 - m + 1
зи (т> 0.75), при 1---— ----
1 - 2m
72m(l + 2m) < а < 1--
1 - 2m
они оказываются устойчивы, причем обе. Это означает, что, помимо явной бистабильности, в системе (4) также реализуются несинфазные циклы длины 1 (х10 = х„ = х„ + 1 * у„ = у„ + 1 = у10 или 5ц = Х„ = Тв+1 *уп= у„ + 1 = уи). Данная пара точек так же, как и в предыдущих случаях, испытывает бифуркацию слияния, причем дважды.
На рис. б б-г показаны эллипсы, на пересечении которых находятся указанные особые точки. Несложно проследить их эволюцию. Слева в заштрихованной области наблюдаются 4 особые точки, две из которых с отрицательными координатами при пересечении границы а = 1/(1 - 2щ) сливаются с нулевой точкой. Вне заштрихованных частей параметрической плоскости существуют только две особые точки - х0 = у0 = 0 и
-
- _ - _ а-1
— ух --—. Справа в заштрихованной части отмечается другая конфигурация особых точек. Эллипсы сближаются и значительно растягиваются таким образом, что нетривиальная особая точка А' =у разделяется на пару точек (а1о , у1о ) и (аи , уи ) с полностью положительными координатами. Для определенности в дальнейшем
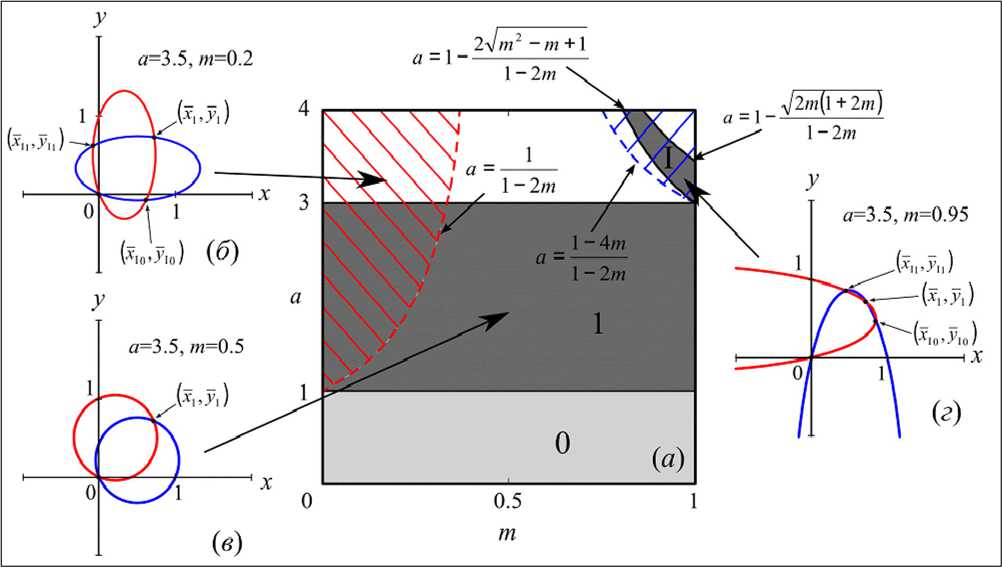
Рис. 6. (а) Области устойчивости особых точек системы (4), (б)-(г) эволюция особых точек
будем считать, что у10 > х10, те. точка (х1о ,у1о ) расположена выше биссектрисы первого квадранта, а Ум <ХЦ’ те- точка (хц’Уц) лежит ниже диагонали. Очевидно, что биссектриса, на которой реализуются чисто синхронные режимы, в данном случае выступает своеобразной сепаратисой, разделяющей бассейны притяжения этих двух состояний.
На рис. б а также приведена область устойчивости всех особых точек. При 1 < а <3 устойчива нетривиаль-- - 1- а ная точка = 71 = —# которую можно назвать синфазным циклом длины 1, область устойчивости которого обозначена на рис. 6 а цифрой 1. При 0 < а < 1 устойчиво только тривиальное состояние равновесия. Как уже было отмечено, несинфазный цикл длины 1 устой-г^т 2 - от + 1 72от(1+ 2от)
чив при 1 — ----------< а < 1 — --------,
1 - 2от 1 - 2от область устойчивости которого обозначена римской цифрой I.
Рассмотрим теперь механизмы потери устойчивости нетривиальной особой точки (^ = ухХ а также не синфазного цикла длины 1 (х х 0, у: 0 ) или (хи, уп ) Для этого, как и в предыдущем случае, построим бассейны притяжения и карты динамических режимов, приведенные на рис. 7 a-и. Как известно [1, 5], области существования или, вернее, области устойчивости циклов различной длины и степени синхронизации для систем, обладающих мультистабильным характером своих возможных динамических режимов, представляют собой многолистную поверхность. На рис. 7 а показаны некоторые из таких листов.
Первый, самый нижний лист, целиком заполняющий параметрическую плоскость, соответствует полностью синхронным режимам длины циклов, которые обозначены цифрами с индексом ноль. Бифуркации данных режимов происходят аналогично бифуркациям одиночного уравнения Ферхюльста. Причем синхронные режимы в отличие от предыдущего случая возможны всегда, те. всегда существует бассейн притяжения таких режимов.
Последующие листы - это области существования несинхронных режимов. Второй лист, который возникает l~jm 2 - m + 1
при а > 1--, - это последовательность би-
1 - 2m фуркаций полностью противофазных циклов. Противо-
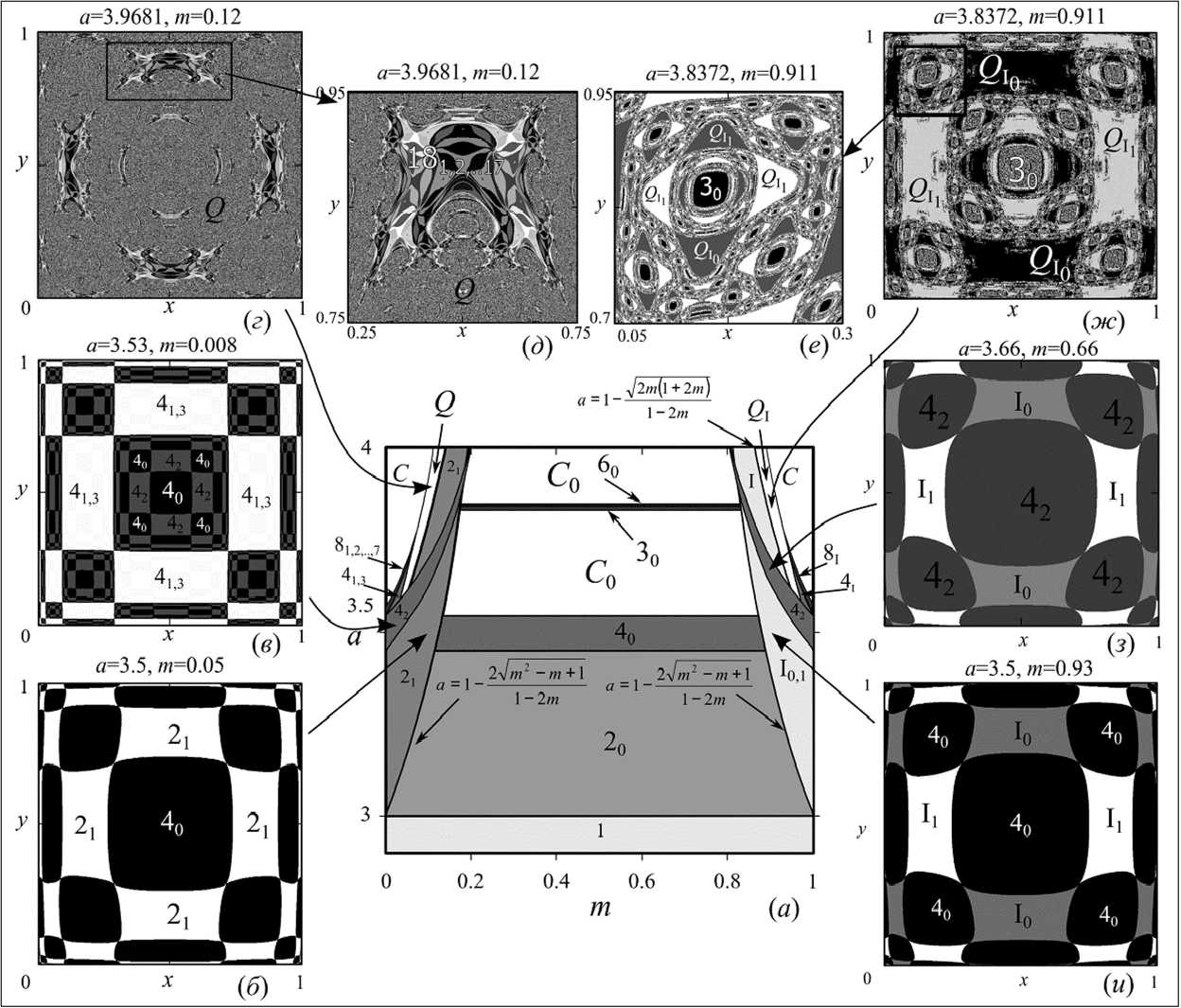
Рис 7. (а) Карта динамических режимов, (б)-(и) примеры бассейнов притяжения, (д) и (е) увеличенные фрагменты бассейнов, демонстрирующие их фрактальную структуру
фазный цикл длины 2 обозначен как 2р длины 4 как 4р 42 или 43 и т.д. В данном случае циклы, обозначенные как N^, - это такие колебательные режимы длины N, которые могут быть реализованы ровно N способами, отличающимися друг от друга временным сдвигом колебательных реализаций системы (4) на количество итераций равное п (и = 0,ф2,...77 — 1). Так циклы с и = 0 соответ ствуют синфазным колебаниям системы, циклы с и ^ О несинфазным.
Бифуркация противофазного цикла 2Z идет в соответствии со сценарием Неймарка-Сакера и сопровождается рождением предельных инвариантных кривых, существующих в области, обозначенной буквой Q, которая «заполнена» окнами периодичности циклов больших длин. Предельные кривые, реализуемые в этой области, формируются вокруг цикла 2Г Область Q заканчивается «окном периодичности», в котором реализуется каскад удвоения периода несинхронных циклов длины 4 и 8, обозначенных как 4г 3 и 8Z2 7, приводящий к возникновению хаотического аттрактора, полностью заполняющего большую часть фазового пространства. Эта область обозначена буквой С, а буква Со соответствует области, в которой формируются синхронный хаотический аттрактор, целиком лежащий на биссектрисе первого координатного угла.
Особо выделяется область существования несинхронного цикла длины 4, обозначенная как 42, «наложенная» на область 2р те. в зависимости от начальных условий в системе (4) могут реализовываться как цикл 2р так и 42, и естественно синхронные циклы. Данные циклы в отличие от 4Z 3 реализуются в окрестности биссектрисы первого квадранта, механизмы возникновения и бифуркации которого остаются неясными.
В случае сильной миграционной связи ( т > 0,7 5) в системе (4) наблюдается так называемый несинфазный цикл длины 1 [1], область существования которого обозначена на рис. 7 а римской цифрой I. Его бифуркация сопровождается рождением лишь одной предельной инвариантной кривой вокруг одного из этих циклов (х11,у11) или (х10,у10) Разрушение квазипериоди-ческой динамики сопровождается формированием на их основе противофазных циклов 4Z и 8Z также реализуемых в окрестности одного из несинфазных циклов длины 1 (^п , Ун ) или (х10,у10).
Как и в случае слабой миграционной связи, при сильной связи также выделяется одиночная область 42, в которой одновременно сосуществуют несколько видов несинхронной периодической динамики: несинхронный цикл длины 42 (схожий аналогичному режиму в левой части рис. 7 а), несинхронный цикл длины 1 (I), ква-зипериодическая динамика (gz) и естественно синхронная динамика - самый нижний лист рис. 7 а.
В дополнение к карте динамических режимов на рис. 7 (б)-(м) приведены бассейны притяжения некоторых из указанных аттракторов. Рис. 7 би в иллюстрируют тот факт, что в зависимости от начальной точки итерирова ния в системе (4) одновременно существуют циклы разной длины и степени синхронизации. Для этого на бассейнах, помимо значений параметров, указаны виды циклов, которые сформируются из начальных условий, взятых из данных областей.
Бассейны на рис. 7 з и и демонстрируют, что область притяжения несинфазного цикла длины 1 (х1о,у1о), расположенного выше биссектрисы первого координатного угла, хоть и содержит саму эту точку, но включает в себя также части фазовой плоскости, расположенные ниже диагонали. Аналогично устроен бассейн притяжения состояния (xzi,yz3 расположенного ниже диагонали. При последующих бифуркациях этих циклов наблюдается та же особенность, в том числе и для бассейнов притяжения предельной инвариантной кривой (рис. 7 ж), формируемой вокруг точек (х11,у11) или (xi о ’ 44 о )■ На рис. 7 ж также можно видеть, что в системе (4) при данных параметрах формируется либо квазипе-риодическая динамика, либо синхронный циклы 3.
На рис. 7 е показан увеличенный фрагмент бассейна, показанного на рис. 7 ж, который вследствие бесконечно большого разнообразия реализаций одной предельной кривой демонстрирует фрактальную структуру бассейна квазипериодической динамики. Аналогично на рис. 7 б показан фрагмент рис. 7 г, демонстрирующий фрактальную структуру бассейна притяжения несинхронного цикла длины 18, вернее, бассейнов его 17 видов (с различной степенью фазовой синхронизации), и квазипериодической динамики, реализуемой в области Q.
Исследование динамических режимов и механизмов формирования нерегулярной динамики систем (4) и (5) показывает, что пространственная динамика популяций с различными типами связи (инерциальной и диссипативной) характеризуются различными режимами синхронизации. При первом типе, когда особи мигрируют в обход процессам локального воспроизводства, наблюдаются преимущественно несинхронные режимы, особенно при больших значениях миграционных параметров. Данный режим синхронизации указывает на то, что каждая локальная популяция испытывает периодический наплыв мигрантов, приводящий к перенаселению и огромному оттоку особей на сопредельную территорию либо высокую смертность к концу следующего сезона. При втором типе миграционной связи, когда особи мигрируют в промежутках между сезонами размножения, формируются преимущественно синхронные режимы. Режим полной синхронизации указывает прежде всего на тот факт, что происходит полная компенсация числа эмигрантов и мигрантов. С другой стороны, бифуркационные механизмы полностью синхронных режимов идут аналогично бифуркациям одиночного уравнения Ферхюльста. Это означает, что при данных значениях популяционных и миграционных параметров и начальных значениях численностей для описания динамики двух миграционно-связанных популяций достаточно использовать одно одиночное уравнение, описывающее дина- мику суммы их численности без потери информации об их внутреннем устройстве.
При инерциальном типе связи полностью синхронные режимы возможны лишь при малых долях миграции т, а при диссипативной связи формирование несинхронных режимов становится возможным при малых или, наоборот, больших долях миграции т. В свою очередь, вследствие сильно раздробленного характера бассейнов притяжения каждого из этих режимов, формирование конкретного режима является достаточно случайным событием, так как малые изменения численности или параметров могут сместить численность популяции в бассейн другого режима синхронизации. Последнее может сопровождаться режимами с частичным захватом частоты, фазы и амплитуды колебания численности и выглядеть как почти синхронная динамика, с последующим уходом на полностью несинхронные режимы, что весьма похоже на явление перемежаемости. Однако здесь это явление носит принципиально иную природу, вызванную именно переходами численности из одного бассейна в другой и связанную с малыми флуктуациями параметров и численности популяции, вызванных неучтенными факторами.
Заключение
В работе рассмотрено два подхода описания пространственной динамики популяций или метапопуляций, состоящих из двух миграционно-свзанных групп особей. Для описания популяций, характеризующихся непрерывным процессом воспроизводства и миграции особей, удобно пользоваться системами обыкновенных дифференциальных уравнений. Исследование качественного поведения таких моделей показало, что подобные популяции характеризуются наличием единственного устойчивого стационарного состояния. Динамика численности при этом носит достаточно монотонный характер -стремление к нетривиальному стационарному состоянию, а флуктуации численности объясняются лишь изменениями параметров и начальной численности.
Для описания динамики численности миграционно-свзяанных популяций, особи которых имеют ярко выраженный сезонный характер воспроизводства и миграции, логично воспользоваться системами связанных логистических отображений. В области устойчивости единственного стационарного состояния в этом случае также наблюдается монотонный режим динамики численности. Однако после потери устойчивости этого состояния в таких системах, помимо формирования периодической и нерегулярной динамики, формируются как синхронные, так и несинхронные колебательные режимы. Показано, что миграционное взаимодействие в таких популяциях может осуществляться двумя способами -инерциальным и диссипативным. При первом способе, когда особи популяции мигрируют в обход процессам локального воспроизводства, наблюдаются преимущественно несинхронные режимы. Кроме того, в этом случае при больших значениях доли мигрантов появляется бистабильный режим динамики - несинхронный цикл длины 1. При втором, когда особи мигрируют в промежутках между сезонами размножения, формируются преимущественно синхронные режимы. Анализ механизмов формирования таких режимов с разной степенью синхронизации, выполненный, в том числе, с использованием показателя синхронизации, предложенного в ранее опубликованной авторской работе [5], показал, что формирование конкретного режима является достаточно случайным событием, так как малые изменения численности или параметров могут сместить численность популяции в бассейн другого режима синхронизации.
Исследование выполнено при финансовой поддержке ДВО РАН (конкурсные интеграционные проекты с СО РАН 12-II-CO-06-019, конкурсный проект 12-1-П28-02) и РФФИ (региональный проект 11-01-98512-рвостока).
Список литературы Подходы к описанию пространственной динамики миграционно-связанных популяций: анализ синхронизации циклов
- Безручко Б.П., Прохоров М.Д., Селезнев Е.П. Виды колебаний, мультистабильность и бассейны притяжений аттракторов симметрично связанных систем с удвоением периода//Изв. вузов. «ПНД». 2002. Т. 10, № 4. С. 47-67.
- Ван Д., Ли. Ч., Чоу Ш.-Н. Нормальные формы и бифуркации векторных полей на плоскости/пер. с англ. под ред. Ю.С. Ильященко. М.: МЦНМО, 2005. 416 с.
- Кузнецов С.П. Универсальность и подобие связанных систем Фейгенбаума//Изв. вузов. Радиофизика. 1985. Т. 27, № 8. С. 991-1007.
- Кулаков М.П., Ревуцкая О.Л. Применение метапопуляционного подхода к анализу пространственно-временной динамики промысловых животных (на примере популяций кабана и изюбря)//Региональные проблемы. 2011. Т. 14, № 2. C. 12-20.
- Кулаков М.П., Фрисман Е.Я. Синхронизация 2-циклов в системе симметрично связанных популяций, запас -пополнение в которых описывается функцией Рикера//Изв. вузов. «ПНД». 2010. Т. 18, № 6. С. 25-41.
- Курилова Е.В., Кулаков М.П., Хавинсон М.Ю., Фрисман Е.Я. Моделирование динамики добычи минеральных ресурсов в регионе: эконофизический подход//Информатика и системы управления. 2012. № 4 (34). С. 3-13.
- Пиковский А., Розенблюм М., Куртес Ю. Синхронизация. Фундаментальное нелинейное явление. М.: Техносфера, 2003. 580 с.
- Примак Р. Основы сохранения биоразнообразия/пер. с англ. О.С. Якименко, О.А. Зиновьевой. М.: Изд-во научного и учебно-методического центра, 2002. 256 с.
- Свирежев Ю.М., Логофет Д.О. Устойчивость биологических сообществ. М.: Наука, 1978. 352 с.
- Хавинсон М.Ю., Кулаков М.П., Мищук С.Н. Математическая модель динамики численности экономически активного населения и иностранной рабочей силы в регионе (на примере еврейской автономной области)//Информатика и системы управления. 2012. № 1 (31), С. 95-106.
- Derin B. Wysham, Alan Hastings. Sudden Shifts in Ecological Systems: Intermittency and Transients in the Coupled Ricker Population Model//Bulletin of Mathematical Biology. 2008. N. 70. P. 1013-1031.
- Frisman E.Ya. Differences in densities of individuals in populations with uniform ranges//Ecological Modelling. 1980. V. 8. P. 345-354.
- Ilkka A., Hanski I., Oscar E. Gaggiotti. Ecology, Genetics and Evolution of Metapopulations. Academic Press. 2004. 696 p.


