Подходы к построению моделей динамики древесных сообществ
Автор: Колобов А.Н.
Журнал: Региональные проблемы @regionalnye-problemy
Рубрика: Региональный прогноз. Математическое моделирование
Статья в выпуске: 1 т.15, 2012 года.
Бесплатный доступ
В работе рассмотрены различные подходы построения моделей динамики лесных экосистем, сформировавшиеся на сегодняшний день. Показаны основные типы моделей и их характеристики. Приведена подробная классификация моделей древесных сообществ по степени детализации и дано их краткое описание. Обсуждаются наиболее перспективные направления развития рассматриваемого леса.
Модели древесных сообществ, индивидуально-ориентированные модели, классификация моделей, основные подходы моделирования леса
Короткий адрес: https://sciup.org/14328793
IDR: 14328793 | УДК: 51-76:577.38
Текст научной статьи Подходы к построению моделей динамики древесных сообществ
Центральным звеном в структуре практически любого биоценоза являются сообщества растений. Они служат не только основными источниками органического вещества, но оказываются теми компонентами, которые целиком определяют его облик и строение. Основная трудность, с которой сталкиваются исследователи при изучении лесных древесных сообществ, связана с длительностью процессов их развития. Для описания динамики лесных ценозов и возможностей управления ими широко применяются средства математического и компьютерного моделирования. Сегодня в науке активно разрабатываются различные типы моделей лесных экосистем [6, 11,16,18, 28, 39], что вызвано сложностью изучаемого объекта. В основном они используются для анализа воздействия различных систем рубок, нарушений, вызванных влиянием внешних факторов (пожары, сплошные рубки, вспышки насекомых и т.д.), естественного развития леса, баланса углерода и климатических изменений.
К настоящему времени разработано большое количество моделей лесных экосистем. Начинающему исследователю трудно разобраться во всем этом многообразии, сложно определиться с выбором подходов и методов моделирования. Многие существующие обзоры моделей касаются только отдельных типов моделей, не раскрывающих общей картины. Цель данной работы -показать основные подходы к построению моделей динамики древесных сообществ, что позволит лучше понять механизмы их функционирования и определиться с методами при решении задач лесопользования и анализа воздействия внешних и внутренних факторов на динамику древесных сообществ.
Модели динамики древесных сообществ
Моделирование леса имеет довольно долгую историю в лесоведении. Уже в 1850-е годы ученые Централь ной Европы использовали графические методы моделирования роста и урожайности лесов [50]. Развитие компьютерных имитационных моделей роста и управления лесами относится к 1960-м годам [42]. В течение последних десятилетий написано большое количество работ, в которых обсуждаются различные типы моделей лесных экосистем [37, 43].
Несмотря на то, что назначение, структура, выходные переменные моделей могут отличаться, их можно объединить в три группы по степени общности описываемых процессов: эмпирические, полуэмпирические, теоретические (рис. 1). Эмпирические модели, получаемые путем усреднения большого количества наблюдений, представляют собой математические выражения, аппроксимирующие с использованием тех или иных критериев приближения, данные измерений. Для них не требуется получения представлений о строении и внутреннем механизме связей в системе. Теоретическая модель описывает абстрактную систему, для первоначального вывода ее соотношений не требуется данных о наблюдениях за конкретными системами. Она строится на основе обобщения априорных представлений о структуре системы и механизмах связей между слагающими ее элементами. Для полуэмпирических моделей математические выражения получаются теоретическим путем с точностью до эмпирически определяемых констант, либо в общей системе соотношений наряду с теоретическими выражениями используются и эмпирические.
По назначению модели можно разделить на четыре основных категории (рис. 1) - роста и урожая, сукцессии, имитации лесопользования, процессные [44]. Такое деление является весьма условным, так как многие из них обладают разными свойствами и одновременно могут быть отнесены к нескольким категориям. Поэтому их можно выделить в отдельный класс гибридных моделей.
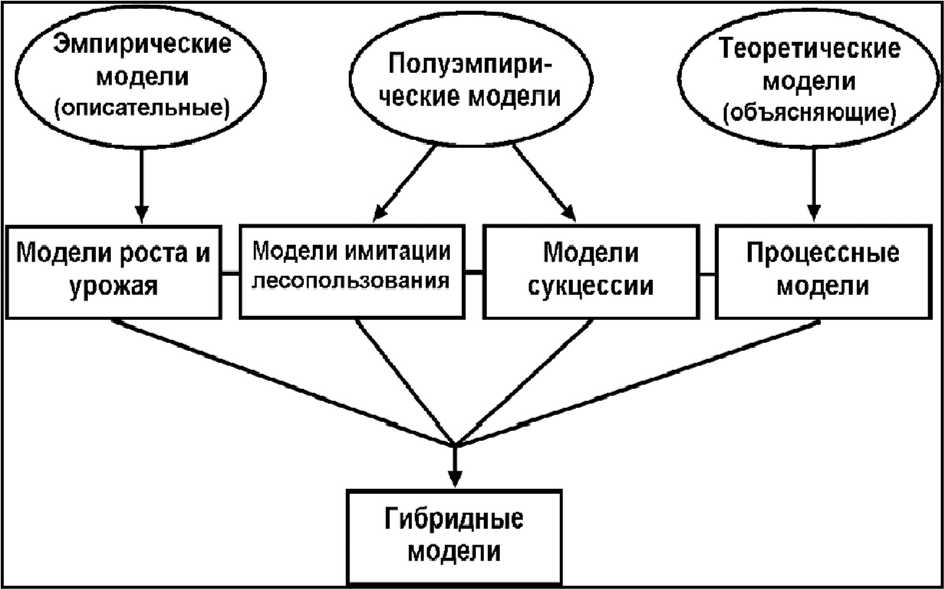
Рис. 1. Основные типы моделей лесных экосистем по степени общности описываемых процессов
Истоки современных систем моделирования леса лежат в развитии таблиц роста древостоев, составленных в Германии в конце XVIII века [50]. Большое количество накопленных данных по инвентаризации лесов и оценке существующих объемов древесины привело к развитию моделей роста и урожая как эффективных инструментов для построения прогнозов в лесопользовании.
Эмпирические модели роста и урожая основываются на большом количестве полевых данных и описывают темпы роста древостоя с помощью функций регрессии. В качестве переменных обычно используют: общий объем древостоя, количество деревьев на участке, плотность, возраст, средний диаметр и высоту деревьев.
Использование термина «модель роста и урожая» в целом относится к формальному математическому описанию, которое позволяет прогнозировать рост и урожай насаждений в широком диапазоне условий. Модель может включать в себя ряд математических уравнений, численные значения параметров уравнений и программный алгоритм, реализуемый на ЭВМ. Выходные данные могут быть отражены в графической или табличной форме. Рост означает увеличение одного или нескольких параметров насаждения в течение определенного периода (например, рост запаса деревьев), а урожай определяется окончательными размерами в конце данного промежутка времени (например, общий запас деревьев).
В одновозрастных насаждениях уравнение роста позволяет прогнозировать рост диаметра, объема на единичном участке в год в зависимости от возраста и других характеристик древостоя, а уравнение урожая -диаметр или общий объем, который достигает древостой к данному моменту времени. Рост и урожай математически выражаются следующим образом, если у - урожай, то рост является производной dy/dt.
Эти модели можно обобщить при описании динамики лесных насаждений, учитывая рост, отпад и другие изменения состава и структуры древостоя. Они ис пользуются для проектирования лесохозяйственных мероприятий, включая разработку эффективных стратегий управления, учета лесов, мониторинга; обеспечивая необходимую эффективность и точность количественной информации для ведения лесного хозяйства. Эмпирические модели роста и урожая позволяют делать прогнозы в рамках таких временных масштабов, когда в условиях роста не ожидается значительных изменений. Так как большинство из них не учитывают влияние климата в качестве фактора, определяющего динамику леса, поэтому они не используются для анализа последствий климатических изменений [47].
Модели имитации лесопользования обычно строятся для прогнозирования прироста древостоя на 10-20 лет в рамках различных режимов рубок [31]. Их можно разделить на дистанционно-зависимые модели, в которых отдельные деревья рассматриваются в пространственно явном виде на основе их точного местоположения [38], и дистанционно-независимые, когда координаты деревьев не учитываются [49].
Рост деревьев в большинстве из них рассчитывается на основе потенциального прироста, который является видоспецифичным и зависит от месторасположения. Этот потенциал уменьшается в результате конкуренции и других ограничивающих факторов [46]. Функции роста могут быть основаны на эмпирических данных с использованием уравнений регрессии [49]. Может использоваться механистический подход, описывающий рост каждого дерева путем вычисления потенциально чистой ассимиляции углерода [26]. Все они учитывают процессы конкуренции за свет. В качестве базовой переменной, как правило, рассматривается прирост диаметра или высоты [46], остальные переменные (объем ствола, диаметр и высота кроны) рассчитываются с использованием аллометрических отношений между ними, которые в общем виде представляют собой степенную зависимость у = ахь.
Во многих моделях имитации лесопользования не рассматривается отмирание деревьев в результате старения, так как предполагается, что взрослые деревья подвергаются рубкам. Например, в работе [29] отпад деревьев осуществляется только в результате недостаточности световых ресурсов.
Модели сукцессии включают в себя явное представление основных экологических процессов, таких как воспроизводство, рост, конкуренция, гибель и круговорот питательных веществ. (Сукцессия (от лат. succesio -преемственность, наследование) - последовательная необратимая и закономерная смена одного биоценоза другим на определённом участке среды во времени.) Они предназначены для моделирования роста и динамики смешанных разновозрастных древостоев, позволяя улавливать переходные характеристики растительности при изменении окружающей среды [21]. Первой моделью, описывающей процессы сукцессии в смешанных разновозрастных древостоях, является JABOWA (названа в честь авторов Janak, Botkin, Wallis), которая более подробно будет обсуждаться ниже [22]. За последние десятилетия создано большое количество моделей сукцессии для различных лесных экосистем [21, 23]. Многие из них применяются для прогнозирования количества деревьев и видового состава в условиях изменения климата [23].
Процессные модели представляют собой формальное математическое описание основных биологических процессов, контролирующих поведение экосистемы, используя параметры, имеющие прямое эколого-физиологическое истолкование. Они предлагают основу для исследования и создания альтернативных гипотез, позволяют выяснять качественные особенности поведения моделируемого объекта, возможные изменения при вариации параметров, помогают точно описать взаимодействие процессов жизнедеятельности деревьев при изменении внешних условий [36]. Применение экологофизиологических принципов дает возможность строить долгосрочные прогнозы в изменяющихся условиях окружающей среды [30].
Верификация моделей производится по экспериментальным данным, что позволяет проверять гипотезы, положенные в их основу. При этом для осуществления сложных процедур калибровки и проверки, как правило, требуется большое количество полевых данных.
Процессные модели используются для объяснения причин и следствий, описывают не одну конкретную, а целый класс экосистем, что делает их более гибкими по сравнению с эмпирическими. Однако они в меньшей степени предназначены для прогноза структуры и продуктивности лесов на определенном участке [52].
В работе [35] широко обсуждаются преимущества и недостатки использования эмпирических и теоретических моделей для устойчивого лесоуправления. Как правило, слабость одних воспринимается как сильная сторона других и наоборот. Тем не менее, они объединяются в гибридные, где недостатки обоих подходов в некоторой степени можно преодолеть [33]. Гибридный подход, связывающий эмпирические модели роста и урожайности с процессными, позволяет разрешать многие проблемы, возникающие при изучении лесных экосистем, таких как прогнозирование динамики смешанных древостоев, анализ реакции леса на изменение окружающей среды [43]. По мнению А.С. Комарова и ОТ. Чертова [12], именно такой подход представляет наиболее перспективную область развития моделирования леса.
Подходы к моделированию лесных экосистем
Как уже было сказано, за последние сорок лет разработано большое количество моделей лесных экосистем, которые различаются между собой по сложности, назначению, использованию разных методов моделирования. В связи с этим предлагаются различные классификации [9, 23, 28, 31, 45], они не всегда бывают однозначными и в некоторых случаях противоречат друг другу. Возникающие трудности при классификации этих моделей связаны с тем, что они могут одновременно обладать различными свойствами и направлены на решение нескольких задач. В данной работе предлагается классификация по степени детализации описываемого объекта (рис. 2). В ней отражены основные подходы к построению моделей, что позволяет лучше понять механизмы их функционирования. Однако следует иметь в виду, что отнесение модели к одному конкретному классу не всегда бывает легко и однозначно.
По степени детализации описываемого объекта модели динамики древесных сообществ можно разделить на две основные категории: индивидуально-ориентиро-ванные и мозаично-ячеистые.
Индивидуально-ориентированный подход позволяет рассматривать динамику моделируемой системы как результат взаимодействия множества дискретных объектов, из которых она состоит, расположенных в пространстве и изменяющих с течением времени свои характеристики согласно тем или иным правилам. Поскольку минимальной структурной единицей моделирования при таком подходе является дерево, то оно может рассматриваться в сообществе с различной степенью детализации его свойств и характеристик. В мозаично-ячеистых моделях древесное сообщество разбивается на небольшие участки земли фиксированной площади, в пределах 20x20 метров. На каждом из них отдельно моделируется динамика биомассы, суммарное количество деревьев, видовой состав, распределение по ступеням толщины и т.д. Учитывается влияние со стороны соседних участков.
Если в индивидуально-ориентированных моделях задаются координаты каждого дерева, то они являются дистанционно-зависимыми, если не учитываются, то -дистанционно-независимыми или gap моделями.
Gap (с англ, gap - разрыв, окно) является условной географической ячейкой - участком фиксированной площади (обычно 10x10 м), на котором имитируется рост, рождение и гибель каждого дерева в зависимости от биотических (конкуренция) и абиотических факторов (климат и почва). Деревья характеризуются определенным набором переменных: вид, возраст, высота, диаметр, объем и т.д. Уравнение роста зависит от светового режима, температуры и других параметров среды, а также от конкуренции за ресурсы жизнедеятельности. Вли-
Индивидуально-ориентированные модели
Мозаичноячеистые модели
Дистанционнозависимые модели
Дистанционнонезависимые (Gap модели)
Дистанционнонезависимые или модели насаждения
Дистанционнозависимые модели
--TROLL
--COMMIX
--FOREST
--SILVA
— FINNFOR
—SYMFOR
— SORTIE
— EFIMOD
— JABOVA —FORSKA — ForClim — ZELIG —FORCAT — PICUS —FORECE — SIMA — ForGra — HUNGER — SORTIE — FireSUM
Модели среднего дерева
—model of Husch —model of Nillson — model of Mulloy — модель Купрова — модель Хильми
Когортные модели
Матричные модели
Цепи Маркова 1, 2-го порядка
— model of Hunta ——model of Horn — модель Логофета
™ j Матрицы Лесл
и
— FORMIX2
— MOSAIC
— model of Wissel
— model of Riera
Дискретный подход с непрерывными функциями роста
Локальные по пространству
модель Корзухина модель Недорезова
Распределенные по пространству
model of Enright model of Osho
модель Апонина модель Антоновского
Обобщенные матрицы
—model of Buongiorno and Michie I—model of Takada and Nakashizuka
Puc 2. Подходы к моделированию древесных сообществ по степени детализации описываемого объекта яние соседних gap, как правило, не учитывается. Одной из первых gap моделей считается JAB0WA [22], в основе построения которой лежат следующие положения:
-
1. Лес рассматривается как совокупность множества небольших участков (gap), каждый из которых может различаться по возрасту и стадии сукцессии. Размер участка выбирается так, чтобы на нем могло разместиться отдельное крупное дерево, занимая при этом доминирующее положение; в JAB0WA размер gap составляет 10x10 м2.
-
2. Участки не взаимодействуют друг с другом, динамические процессы роста в каждом из них описываются отдельно. Моделируемый древостой представляет собой мозаику независимых gap.
-
3. Позиции деревьев в gap не учитываются, они считаются горизонтально однородными.
-
4. Листья каждого дерева расположены в бесконечно тонком слое, представляющем собой диск в верхней части ствола.
-
5. Предполагается, что виды имеют неограниченный источник семян на моделируемом участке.
-
6. Рост моделируется как детерминированный процесс, отпад и воспроизводство являются случайными.
-
7. Конкуренцией между деревьями и другими формами растительности (кустарники, трава) можно пренебречь.
На базе JAB0WA было создано много других gap моделей, имеющих значительные различия, но, как правило, сохраняющих общие принципы, лежащие в ее основе. Большинство из них состоят из трех основных блоков: воспроизводство, гибель и рост.
Функция роста дерева в этих моделях описывает потенциальный прирост, который зависит от качества участка. Максимальный потенциал снижается за счет «функции отклика» в зависимости от светового режима, температуры, влажности и в некоторой степени от питательных веществ. Например, в JABOWAnpHpocT диаметра каждого дерева рассчитывается по следующей формуле:
dt \ dbh - h И1
V max " max V где R - параметр роста (зависит от скорости фотосинтеза), LA - листовая поверхность, dbh - диаметр на высоте груди, h - высота дерева.
Отпад деревьев учитывается под влиянием двух факторов: 1) отмирание в результате старения и 2) конкуренции за ресурсы жизнедеятельности, когда ежегодный прирост диаметра становится ниже определенного минимального значения характерного для данного вида [23]. Прорастание семян зависит от наличия света в лесной подстилке и других экологических условий (например, почвенной влаги, азота, температуры, ощипывания молодых побегов).
Примером индивидуально-ориентированной, дистанционно-зависимой модели может служить известная российская модель EFIMOD [34]. Она позволяет проводить прямую оценку влияния климата, плодородия почв и лесохозяйственных мероприятий на рост чистых и смешанных древостоев, круговорот углерода и азота в лесных экосистемах бореальной и умеренной зон. Рост отдельных деревьев имитируется в зависимости от их позиции на участке и локально доступных ресурсов: света, воды и азота. Каждое дерево состоит из пяти компонентов: ствол, ветви, листья/хвоя, толстые корни, тонкие корни. Прирост биомассы зависит от света и азота, учитывается влияние климатических и почвенных условий. Знание точных позиций деревьев позволяет легко имитировать различные виды рубок и их возможные последствия.
Мозаично-ячеистые модели также можно разделить на дистанционно-зависимые и дистанционно-независимые. В первом случае насаждение рассматривается как мозаика участков, расположенных в пространстве и оказывающих взаимное влияние друг на друга. На каждом из них отдельно моделируется динамика биомассы, суммарное количество деревьев, видовой состав, возрастные стадии развития. В большинстве случаев состояние участков характеризуется как дискретное (возраст, стадия сукцессии). Переход от одного состояния к другому рассчитывается с использованием вероятностей. Однако рост деревьев внутри ячейки не моделируется в явном виде.
Модель FORMIX описывает динамику смешанных влажных тропических лесов с использованием вероятности перехода из одного класса полога в другой [32]. Территория делится на ячейки 20x20 метров, каждая из которых разбивается по высоте на пять слоев. Переход деревьев из одного слоя в другой оценивается с помощью вероятностей. Рост, гибель и воспроизводство внутри ячейки зависят от состояния соседних участков. Динамика количества деревьев ^ и биомассы В в пределах каждого слоя г (класс по высоте) и группы j (деление на группы по теневыносливости) описывается следующими дифференциальными уравнениями:
dN, ,—— = TN.-TN-MT, (2)dt где TNT_V TN; - количество деревьев, переходящих в слой / и выходящих из него, MTt - коэффициент смертности.
где Btj- биомасса деревьев z'-го слоя, j - группы, РВ1} - фотосинтетическое производство, RtJ - потери в результате дыхания, опада листвы, ветвей; третий параметр показывает переход из одного слоя в другой; четвертый определяет потери в результате гибели деревьев.
В дистанционно-независимых моделях насаждения древесное сообщество рассматривается как единое целое. Они имитируют динамику лесных массивов с обобщенными показателями (общая площадь, биомасса, количество деревьев, плотность, средний диаметр, высота, возрастные группы и т.д.), иногда с очень детальным рассмотрением экофизиологических процессов.
Простая, но довольно эффективная эколого-физиологическая модель насаждения была предложена Хильми [15]. Она описывает динамику запаса древостоя и сводит к следующему уравнению:
— (4)
где IF- запас древостоя, А - максимальное значение запаса, Т] - доля биомассы древостоя, теряемая за год. Это уравнение дает хорошее совпадение с табличными данными по запасу различных древесных сообществ.
Модели насаждения можно разделить на две группы: среднего дерева и когортные. Первые фактически представляют собой уравнения и таблицы роста и урожая, которые были рассмотрены выше. Они не учитывают гетерогенность насаждения по пространству и другим параметрам, исключение может составлять видовой состав. Некоторые из них описывают межвидовые взаимодействия, когда на рост, гибель и возобновление одного вида влияют другие.
Одно из первых эмпирических уравнений роста древостоя было предложено в работе [41], оно представляет собой линейную регрессию и базируется на предположении, что относительная скорость роста изменяется обратно пропорционально возрасту
1п(Ю = Д - Д -Г1, (5)
где V - объем древостоя, /?0 - значение верхней асимптоты, Рх - параметр, характеризующий скорость роста. Эти параметры отражают условия произрастания и плотность древостоя.
В основе многих теоретических моделей среднего дерева лежит уравнение Берталанфи [20], которое описывает скорость изменения биомассы как разность между интенсивностями фотосинтеза и дыхания dY
— = PJ " PJ. (6) dt где F - биомасса насаждения, а - параметр, характеризующий прирост в результате фотосинтеза, ^х .р^ -постоянные.
Дальнейшим развитием моделей среднего дерева является использование системы уравнений для описания роста разновозрастных древостоев. Например, в работе [4] предложена модель динамики однопородных насаждений, которая сводится к следующей системе:
'№ = Mt0)cxp[- (a, + a2)(/ - /0)] - {1 + a2 (t - 10 ) + + «2 (1 " 10 )Z(a3 “ “ «2 ) “ a2 Z(a3 ~ " «2 У X x [1 - exp((a, + a2 - a3 Xt - t0))]} dH _dx«\- ехр(-с73ЛТ72))
dt d3NH2 2
D = D(t0)+ ln[(62 -b^Kb, -//)]■№, -М/Ц1 - dV ct ((1 - exp(-c3^D2)) --=--c ^ VH dt c3N
W =NV dO
— = -eVdN / dt
, dt где ^-число стволов, шт./га; Н - средняя высота, m;D -средний диаметр, см; V - средний объем дерева, м3; W -запас древостоя, м3/га; О - отпад, м3/га. Она позволяет с достаточно высокой точностью описывать динамику основных таксационных показателей различных однопородных древостоев.
В когортных моделях структура насаждения описы-вается с использованием размерных (диаметр, высота), возрастных групп, а также состояний системы (тип растительности, видовой состав). Такие модели делятся на два основных вида. К первым относятся матричные модели, в которых для каждого временного шага задается вероятность перехода из одного размерного класса в другой. Размеры деревьев внутри когорт не рассчитываются, поскольку предполагается равномерное распределение. В основе их построения используется матричная алгебра. В когортных моделях второго вида используют непрерывные функции роста внутри каждого дискретного класса. Переход между классами описывается с помощью постоянных коэффициентов.
Матричные модели широко применяются в экологии [25]. Они моделируют динамику древостоя путем его деления на фиксированное число стадий развития (например, по возрасту, высоте или диаметру). Считается, что доля особей в каждом классе изменяется дискретно с каким-то временным шагом. Такие модели являются эмпирическими, поскольку экологические процессы, которые определяют эти изменения, не описываются в явном виде, а только считается их суммарный эффект. Используемые математические средства в этих моделях делятся на четыре группы: марковские цепи первого, второго порядка, матрицы Лесли (или Ушера), обобщенные матрицы.
В основе марковских цепей первого порядка лежат два основных положения: 1) число состояний конечно; 2) вероятность изменения одного состояния в любое другое зависит только от текущего состояния, а не от предыдущих событий в системе. Математически цепь Маркова выражается следующим уравнением: ^+]=Л -N£, где векторы N£ и ^+] содержат вероятности каждого со-
Ги 1 )
стояния системы в момент t и tRl, и мат-
А рица вероятностей перехода ляется стохастической: g $ 1. Марковские цепи первого порядка используются в основном для моделирования изменений типа ландшафта [27], растительности [48], видового состава [51 ].
Цепи Маркова второго порядка позволяют оценивать состояние леса в моменты времени t, в зависимости от его состояния в момент времени 01 и 02. Вероятность перехода деревьев в следующее состояние зависит от двух предыдущих, таким образом, например, определяется тенденция дерева к росту или гибели.
В матрицах Лесли временной интервал и ширина класса выбираются так, что деревья не могут переходить более чем в один класс за один шаг. В отличие от цепей Маркова первого порядка они являются детерминированными. Такие матрицы позволяют учитывать производство семян путем включения соответствующих коэф-
£н + /1
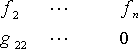
£ n - In £ ПП
фициентов в первую строку:
8 21
О где ^ - коэффициент производства семян, gy - постоянная доля особей, переходящих в следующий класс.
Обобщенные матрицы используют более общие подходы построения матричных моделей, в которых описывается воспроизводство, рост и отпад деревьев в зависимости от плотности. При таком подходе деревья могут переходить более чем в один класс за временной шаг в отличие от матриц Лесли.
Например, в работе [24] количество деревьев в размерных классах по диаметру рассчитывается с помощью следующего уравнения:
N(t + 1) =0^ +R)'(Nim ~Нт) + С, (8) где vV^^- количество деревьев в классе / на предыдущем временном шаге t, Н - вектор, описывающий сбор урожая, С - вектор постоянного появления деревьев в наименьшем размерном классе, Л(^ - матрица перехода и R - матрица воспроизводства, содержит видовое влияние на прорастание других видов.
Матричный подход хорошо развит в ряде российских работ, касающихся построения марковских моделей сукцессии [5, 40].
Во втором типе когортных моделей структура леса также описывается с использованием дискретных размерных классов и вероятностей перехода между ними, но в отличие от матричных рост деревьев в пределах каждого класса описывается с помощью непрерывных функций. Они могут учитывать пространственное распределение растительных сообществ по ареалу обитания или не рассматривать пространственную структуру, предполагая, что деревья размещены равномерно.
Одним из наиболее перспективных подходов в моделировании локальной динамики лесного ценоза является подход, предложенный М.Д. Корзухиным. В рамках математической модели динамики растительного ценоза предполагалось, что деревья могут быть разделены на три группы по высоте. Скорости протекания различных процессов в ценозе - переход между группами, отпад деревьев и появление особей младшего возрастного класса - зависят от численности выделенных групп деревьев:
--- = р w - у (w ) и - fu dt dv
-
< --- = aju - pv - qv
dt dw
--- = Pqv - hw dt где и, V, W - доли проекций площадей крон деревьев младшего, среднего и старшего возрастных классов соответственно; р — коэффициент размножения, интенсивность рождения особей младшего возрастного класса, которая зависит только от численности старшей возрастной группы; у- функция угнетения, интенсивность гибели особей первого яруса под воздействием верхнего яруса; f q - коэффициенты переходов особей в следующую возрастную группу; р, h - коэффициенты отмирания особей средней и старшей возрастных групп соответственно [10].
При этих предположениях в системе реализуются следующие динамические режимы: гибель леса, устойчивое сосуществование деревьев всех трех классов, триггерный режим, при котором одно из положений равновесия тривиальное, стационарный колебательный режим.
Вместе с тем, недостатками данной модели можно считать существование режима гибели леса, который в действительности наблюдается лишь в чрезвычайных ситуациях. Кроме того, определенная некорректность проявляется также в существовании неограниченных решений, возникающих при некоторых значениях параметров и начальных данных.
Распределенные модели, как правило, используют нелинейные дифференциальные уравнения с частными производными. Одна из первых моделей такого типа предложена в работе [19] и имеет следующий вид:
ди о2 и
-
— = pv - g(v)u + -
- J dtdx
dv '(10)
— = и - nv dt
Она описывает пространственно-временную динамику возрастной структуры популяции растений. При этом учитываются только два возрастных класса - молодые и старые особи.
Пространственно-временные эффекты, связанные с процессами размножения растений семенами, учитываются в другой более сложной модели, предложенной в работе [1]:
517 (S2W
ST (ау2
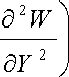
- (В + R)W + ЛИ
SU
--= RW - FU - GU ST
SV
--= FU - HU ST
Здесь MX, E T) - плотность численности семян в момент времени Т в окрестности точки с координатами X, У; Е(Х, У, 7)-плотность численности взрослых особей; U(X, У, Г)- плотность численности младшего класса. Данная модель позволяет проводить вычислительные эксперименты при исследовании динамики отклика распределенной по ареалу популяции растений в ответ на внешние воздействия (пожары, вырубки, лесопосадки), учитывая географические факторы, перемены климата, изменчивости почвенных условий.
Подходы к моделированию роста дерева
Центральным звеном в индивидуально-ориентированных моделях динамики древесных сообществ является описание роста отдельного дерева. Одним из основных этапов моделирования является составление балансовых соотношений, которые в той или иной форме применяются в большинстве современных моделей высших растений, учитывающих деление на отдельные органы. В них важными составными частями являются транспорт и распределение ассимилятов между частями растения.
Одна из широко известных моделей роста свободно растущего дерева, записанная в форме закона сохранения энергии, предложена И.А. Полетаевым [14].
Е - рх 2 + ух4 + 5— (рх3\ (12)
dt где х - линейные размеры дерева, Е - энергия, которую дерево получает в результате фотосинтеза. Первое слагаемое в правой части определяет расход энергии на нужды фотосинтеза, второе - расходы на транспорт ассимилятов, третье - расходы на увеличение массы растения, Р, Y,3, Р- постоянные.
Это уравнение послужило основанием для построения модели роста дерева в светолимитированных древостоях [3].
dH а . .
— =----(1- ехр^рЯ2)) - ЬНг, (13)
dt pH1 v ’ где Н - высота дерева, р - параметр, характеризующий густоту насаждения, а, Ъ - видоспецифичные параметры. Полученное уравнение роста дерева в светолимитированных однопородных древостоях учитывает конкуренцию деревьев за световые ресурсы, позволяя проследить связь между параметрами уравнения и густотой насаждения.
В моделях развития растений балансовые соотношения обычно записываются в соответствии с принципом лимитирующих факторов Либиха-Полетаева [13]. Согласно этому принципу, интенсивность выходного процесса в каждый момент времени определяется наименее интенсивной компонентой входного процесса. В качестве лимитирующих факторов, как правило, выступают физиологически активная радиация (ФАР), концентрация СО2, влажность, температура, питательные вещества. Примером такого типа моделей служит концепция экосистемы одного растения, предложенная ОТ. Чертовым [17], которая может рассматриваться как структурная и функциональная единица при моделировании наземных экосистем. В общем виде ее можно записать как авр dt
p-R-lp,
Р = min
Е
е
w
(Р - R) = min<
п
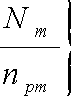
где Р - истинный фотосинтез, R - дыхание, Ер - количество опада растения, Е^ - поглощенная ФАР, 1Га - доступная влага почвы, ^, ■ ..А^ - элементы питания, по требленные из почвы, ер , w р ,п pV..n рт- удельный расход энергии ФАР, влаги и элементов питания на построение единицы прироста биомассы. Выражения под знаком минимума являются формальной записью условия Либиха. Первый минимум предполагает возможность достаточно долгого существования растения при недостатке элементов питания, если оно обеспечено ФАР и водой. Второй определяет роль недостатка элементов питания в продукционном процессе.
Для описания роста дерева в сообществе необходимо учитывать конкуренцию за различные ресурсы жизнедеятельности. Она обычно описывается уравнением
dx
— = кх(1 - л1), dt
где х - размер дерева, X - РесУРЧ к - коэффициент роста. Например, в работе [2] предложена модель, описывающая динамику прироста по диаметру ствола в зависимости от размеров взаимодействующих особей и расстояний между ними. Уравнение роста /-го дерева записывается как
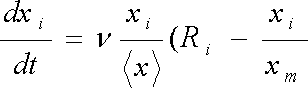
где х^ - диаметр ствола /-го дерева, уС/ — средний диаметр стволов, v - масштабный коэффициент, хт - максимальный диаметр дерева, зависящий от породы, условий местообитания, R^ - описывает конкурентное воздействие на /-е дерево со стороны соседей.
В работах [7, 8] нами предложена эколого-физиологическая модель роста дерева в условиях конкуренции за свет, записанная в форме закона сохранения энергии.
dt а(1 - ехр( - pV d )) ■ Q + Р_ pV d
= (^ + m ■ Я) ■ Мб) -
At I J
где V - объем дерева, Н - высота, D - диаметр, а - начальная крутизна световой кривой показывает зависимость фотосинтеза от интенсивности освещения, р - параметр, характеризующий самозатенение, 7Dmax - максимальная интенсивность фотосинтеза единицы листовой поверхности, Q - доля солнечной радиации при затенении окружающим древостоем, Н тах - максимальная высота, / - видовое число, показывающее отклонение от идеального цилиндра. Она дает достаточно хорошее совпадение с табличными данными хода роста различных видов деревьев.
Заключение
Таким образом, в настоящее время разработано большое количество моделей динамики древесных сообществ, направленных на решение различных задач. Их диапазон довольно широк: от простых одновидовых, описывающих запас древостоя, до сложных, отражающих видовые характеристики и эколого-физиологические процессы.
Возникающие иногда дискуссии, связанные со сравнением и противопоставлением описанных направлений моделирования, на наш взгляд, представляются бесплодными, так как разные подходы имеют несовпадающие области применения. Например, нет смысла привлекать сложные эколого-физиологииесие модели для решения стандартных задач таксации, которые успешно решаются регрессионными методами. Но по мнению автора, наиболее перспективной областью развития моделей динамики древесных сообществ является гибридный подход. Он объединяет в себе различные методы, позволяя учитывать всевозможные свойства и компоненты леса, рассматривая его как некоторую целостную структуру.
Моделирование древесных сообществ характеризуется необходимостью учитывать богатое видовое разнообразие и ярусно-мозаичную неоднородную пространственную структуру. Одним из ведущих процессов, формирующих видовой состав биоценозов, а также пространственное распределение видов в пределах биотопа, является конкуренция. Поэтому при построении моделей леса необходимо уделять особое внимание описанию механизмов внутривидовой и межвидовой конкуренции. При этом нужно учитывать пространственную структуру как основной фактор, влияющий на напряженность конкурентных отношений. Также модель должна быть основана на эколого-физиологических принципах, отражающих основные биологические процессы, контролирующие поведение системы. Все это обеспечивает понимание механизмов функционирования объекта, дает возможность анализировать причин- но-следственные связи и строить долгосрочные прогнозы в изменяющихся условиях окружающей среды.
Развитие компьютерных технологий позволяет реализовать все более сложные вычислительные процедуры, которые перестают быть существенными ограничивающими факторами при построении моделей динамики древесных сообществ.
Исследования проведены при финансовой поддержке РФФИ (проект № 11-01-98512-р_восток_а), ДВО РАН (проект № 12-III-A-09-195).
Список литературы Подходы к построению моделей динамики древесных сообществ
- Апонин Ю.М., Апонина Е.А., Кузнецов Ю.А. Математическое моделирование пространственно-временной динамики возрастной структуры популяции растений//Математическая биология и биоинформатика. 2006. Т. 1, № 1. С. 1-16.
- Борисов А.Н., Иванов В.В. Имитационное моделирование динамики темнохвойных древостоев при выборочных рубках//Хвойные бореальные зоны. 2008. Т. 25, № 1-2. С. 135-140.
- Карев Г.П. Математическая модель роста в светолимитированных древостоях//Журнал общей биологии. 1983. Т. 44, № 4. С. 474-479.
- Карев Г.П., Скоморовский Ю.И. Моделирование динамики однопородных древостоев//Сибирский экологический журнал. 1999. № 4. с. 403-417.
- Князьков В.В., Логофет Д.О., Турсунов Р.Д. Неоднородная марковская модель сукцессии растительности в заповеднике «Тигровая балка»//Математическое моделирование популяций растений и фитоценозов/под ред. Д.О. Логофета. М.: Наука, 1992. С. 37-48.
- Колобов А.Н. Индивидуально-ориентированная модель динамики древесных сообществ//Известия Самарского Научного центра РАН. 2009. Т. 11, № 1(7). с. 1477-1486.
- Колобов А.Н. Численно-аналитическое исследование модели роста дерева в условиях конкуренции за свет//Математическая биология и биоинформатика. 2012. Т. 7, № 1. с. 125-138.
- Колобов А.Н., Фрисман Е.Я. Моделирование процессов конкурентного взаимодействия в древесных сообществах//Сибирский журнал индустриальной математики. 2009. т. 12, № 4 (40). с. 79-91.
- Комаров А.С. Математические модели в популяционной биологии растений//Ценопопуляции растений. Очерки популяционной биологии растений/Л.А. Жукова, Л.Б. Заугольнова, А.С. Комаров, О.В. Смирнова. М.: Наука, 1988. С. 137-155.
- Корзухин М.Д. Возрастная динамика популяции деревьев, являющихся сильными эдификаторами//Проблемы экологического мониторинга и моделирования экосистем. Л.: Гидрометеоиздат, 1980. № 3. С. 162-178.
- Кузнецов В.И., Козлов Н.И., Хомяков П.М. Математическое моделирование эволюции леса для целей управления лесным хозяйством. М.: ЛЕНАНД, 2005. 232 с.
- Моделирование динамики органического вещества в лесных экосистемах/отв. ред. В.Н. Кудеяров. М.: Наука, 2007. 380 с.
- Полетаев И.А. О математических моделях роста//Физиология приспособления растений к почвенным условиям. Новосибирск: Наука, 1973. С. 7-24.
- Полетаев И.А. Проблемы кибернетики. М.: Наука, 1966. T. 16. C. 171-190.
- Хильми Г.Ф. Энергетика и продуктивность растительного покрова суши. Л.: Гидрометеоиздат, 1976. 62 с.
- Хомяков П.М., Конищев В.Н., Пегов С.А. и др. Геоэкологическое моделирование для целей управления природопользованием в условиях изменений природной среды и климата. М.: УРСС, 2002. 398 с.
- Чертов О.Г. Математическая модель экосистемы одного растения//Журнал общей биологии. 1983. Т. 44, № 3. С. 406-414.
- Чумаченко С.И. Моделирование динамики многовидовых разновозрастных лесных ценозов//Журнал общей биологии. 1998. Т. 59, № 4. С. 363-376.
- Antonovsky M.Ya., Aponina E.A., Kuznetsov Yu.A. Spatial-temporal structure of mixed-age forest boundary: the simplest mathematical model. WP-89-54. IIASA. Laxenburg. Austria. 1989.
- Bertalanffy L. Unterschungen uber die Gesetzlich beit des Wachstums. VII. Stoffwechseltypen und Wachstumstypen//Biologisches Zentralblatt. 1941. V. 61. P. 510-532.
- Botkin D.B. Forest Dynamics: An Ecological Model. Oxford University Press. Oxford and New York. 1993. 309 p.
- Botkin D.B., Jamak J.F., Wallis J.R. Some ecological consequences of a computer model of forest growth//Journal Ecology. 1972. V. 60. P. 849-873.
- Bugmann H. A review of forest gap models//Clim. Chang. 2001. V. 51. P. 259-305.
- Buongiorno J. et al. Growth and management of mixed-species, uneven-aged forests in French Jura: implications for economic returns and tree diversity//For. Sci. 1995. V. 41. P. 397-429.
- Caswell H. Matrix population models: construction, analysis and interpretation. Second Edition. Sinauer Associates. Sunderland. Massachusetts. USA. 2001. 722 p.
- Chave J. Study of structural, successional and spatial patterns in tropical rain forests using TROLL, a spatially explicit forest model//Ecol. Model. 1999. V. 124. P. 233-254.
- Cherrill A.J. Predicting the distributions of plant species at the regional scale: a hierarchical matrix-model//Landsc. Ecol. 1995. V. 10(4). P. 197-207.
- Chertov O.G., Komarov A.S., Karev G.P. Modern Approaches in Forest Ecosystem Modelling//European Forest Institute Research Report N8. Leiden, Boston, Kцln. Brill. 1999. 130 p.
- Courbaud B. et al. Evaluating thinning strategies using a Tree Distance Dependent Growth Model: someexamples based on the CAPSIS software «Uneven-Aged Spruce Forests» module//Forest Ecology and Management. 2001. V. 145. P. 15-28.
- Dixon R.K. et al. Process Modeling of Forest Growth Responses to Environ-mental Stress. Timber Press. Portland. OR. 1990. 441 p.
- Hasenauer H., Burgmann M., Lexer M.J. Konzepte der Waldцkosystemmodellierung. Cent. bl. gesamte Forstwes. 2000. V. 117 (3/4). P. 137-164.
- Huth A., Ditzer T. Simulation of the growth of a lowland Dipterocarp rain forest with FORMIX 3//Ecol. Model. 2000. V. 134. P. 1-25.
- Kimmins J.P., Mailly D., Seely B. Modelling forest ecosystem net primary production: the hybrid simulation approach used in FORECAST//Ecological Modelling. 1999. V. 122. P. 195-224.
- Komarov A.S., Palenova M.M., Smirnova O.V. The concept of discrete description of plant ontogenesis and cellular automata models of plant populations//Ecological Modelling. 2003. V. 170. P. 427-439.
- Landsberg J.J., Coops N.C. Modeling forest productivity across large areas and long periods//Natural Resource Modeling. 1999. V. 12. P. 383-411.
- Landsberg J.J., Gower S.T. Application of Physiological Ecology to Forest Management. Academic Press. San Diego. CA. 1997. 354 p.
- Landsberg, J. Modelling forest ecosystems: start of the art, challenges, and future directions//Canadian Journal of Forest Research. 2003. V. 33. P. 385-397.
- Liu J., Ashton P.S. FORMOSAIC: an individual-based spatially explicit model for simulating forest dynamics in landscape mosaics//Ecol. Model. 1998. V. 106. P. 177-200.
- Liu J., Ashton P.S. Individual-based simulation models for forest succession and management//Forest Ecol. Manage. 1995. V. 73. P. 157-175.
- Logofet D.O., Lesnaya E.V. The mathematics of Markov models: what Markov chains can really predict in forest successions//Ecol. Model. 2000. V. 126. P. 285-298.
- MacKinney A.L., Chaiken L.E. Volume, yield and growth of loblolly pine in the mid-Atlantic coastal region//Appalachian Forest Expt. Sta., 1939, Techn. Note 33. 30 p.
- Newnham R.M. The Development of a Stand Model for Douglas-fir, Ph.D. thesis, University of British Columbia. Vancouver. Canada. 1964.
- Peng C.H. Growth and yield models for uneven-aged stands: Past, present, and future//Forest Ecology and Management. 2000. V. 132. P. 259-279.
- Peng C.H., Wen X. Forest simulation models//Computer Applications in Sustainable Forest Management: Including Perspectives on Collaboration and Integration. Springer. Printed in the Netherlands. 2006. P. 101-125.
- Porte A., Bartelink H.H. Modeling mixed forest growth: a review of models for forest management//Ecol. Model. 2002. V. 150. P. 141-188.
- Pretzsch H., Dursky J. Growth reaction of Norway spruce (Picea abies (L.) Karst) and European beech (Fagus silvatica L.) to possible climatic changes in Germany//Forstw. Cbl. 2002. V. 121. P. 145-154.
- Shugart H.H., Smith T.M. A review of forest path models and their application to global change research//Climatic Change. 1996. V. 34. P. 131-153.
- Starfield A.M., Chapin F.S. Model of transient changes in arctic a boreal vegetation in response to climate and land use change//Ecol. Appl. 1996. V. 6 (3). P. 842-864.
- Sterba H., Blab A., Katzensteiner K. Adapting an individual tree growth model for Norway spruce (Picea abies L. Karst.) in pure and mixed species stands//Forest Ecology and Management. 2002. V. 159. P. 101-110.
- Vuokila Y. Functions for variable density yield tables of pine based on temporary sample plots. Communicationes Instituti Forestalis Fenniae. 1965. V. 60. P. 1-86.
- Yemshanov D., Perera A. A spatially explicit stochastic model to simulate boreal forest cover transitions: general structure and properties//Ecological Modelling. 2002. V. 150. P. 189-209.
- Zhou X. et al. Predicting forest growth and yield in northeastern Ontario using the process-based model of TRIPLEX1.0//Canadian Journal of Forest Research. 2005. V. 35. P. 2268-2280.


