Погрешность упрощенного вычисления средней температуры теплоносителя на участке теплопровода

Постановка задачи. При выполнении теплотехнических расчетов инженерных систем зданий и сооружений часто необходимо определять среднее значение температуры воды (теплоносителя) на участке трубопровода (теплопровода) [1–5]. При этом обычно искомое среднее значение температуры воды вычисляют по упрощенной формуле – по ее температурам в двух точках – в начале и в конце участка [1–5]. Вместе с тем интересно бы знать, какова погрешность такого метода вычисления и в каких случаях такой метод вычисления вполне допустим. В данной работе и рассматривается решение этой задачи для условий стационарного теплообмена.

Распределение температуры теплоносителя вдоль трубы. Понятно, что погрешность упрощенного вычисления средней температуры зависит от того, как температура теплоносителя изменяется вдоль поверхности теплообмена – по длине трубы. Поэтому для решения поставленной задачи следует, в первую очередь, выяснить, как в соот- ветствии с физикой процессов теплообмена и течения в трубах температура жидкости изменяется во времени и в пространстве – по длине трубы. Данная задача рассматривалась в работах [6–10]. Выявлено, что в установившемся режиме распределение температуры теплоносителя по длине теплопровода подчиняется следующему уравнению [6–9]:

t=tВ+(t0-tВ)⋅exp(- πL ), (1) cGRL где t0, t(L) – температура теплоносителя в начале и в точке L по длине теплопровода, tВ – температура окружающей среды, c и G – соответственно теплоемкость теплоносителя и его массовый расход, RL – линейное термическое сопротивление теплопередаче теплопровода.

Как видно из уравнения (1), температура теплоносителя по длине трубы распределяется по экспоненциальной кривой, причем при G →∞ температура теплоносителя во всех точках по длине теплопровода t ^ t0, т. е. она практически не изменяется по длине трубы и равна температуре в начале участка. Если же G^0, то t^tB, т. е. температура теплоносителя во всех точках по длине теплопровода практически мгновенно опускается до температуры окружающего воздуха.

Из уравнения (1) видно, что температура теплоносителя по длине теплопровода является функцией безразмерного комплекса (обобщенной пере менной) X = —-— . На рис. 1 приведен график cGRL

L этой зависимости от комплекса X = ^ при t0 = 90 ° С и tB = 20 ° С . Как видно из рис. 1, ос- новное изменение температуры теплоносителя наблюдается при 0 < X <1,5, что имеет место либо

L при 0 < L <1,5 • cGRL , либо при G >-------.

L                  1,5 • cR L

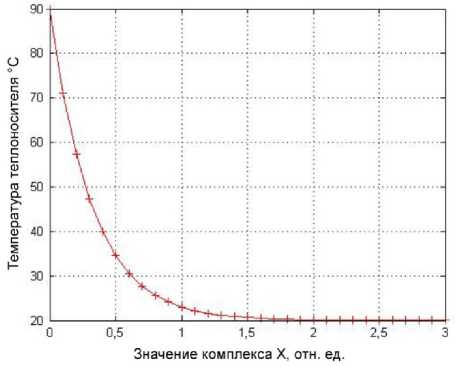
Рис. 1. Зависимость температуры теплоносителя от значения безразмерного комплекса X

Определение погрешности вычисления и анализ полученных соотношений. Известно, что точное значение средней температуры теплоносителя на участке [0; L] вычисляется по формуле

L

Т = - f t ( L ) dL .                             (2)

L ₀

Поэтому, подставляя выражение (1) в формулу (2), получим следующее соотношение:

t" = 7 J t ^{( L} ) ^dL = 7 J [ t B + ⁽ 1 0 ^- t B ) • exP⁽— T L -^{)] dL} =

L ₀        L ₀                  cGR_L

= t_B + ⁽ t 0 t^B ) ^CGR L [1 - exp(     ⁿ L )].             (3)

В      n L            cGR L

Однако для участка [0; L] может быть применена и упрощенная формула вычисления средней температуры теплоносителя, которая имеет вид [1–5]:

_ t ⁰ + 1 ( L ) ^{t yn} =    2

.

Подставляя в формулу (4) выражение (1), получим, что найденная таким образом величина t _УП будет равна следующему соотношению:

t yn = t ⁰ + t B ^{[1 -} exp^{( -} ^ L -^)],               ⁽⁵⁾

2        cGRL которое, как видно, совсем не равно точному значению средней температуры, вычисляемому по формуле (3). Формула (4) будет давать точное значение средней температуры теплоносителя только в том случае, если температура теплоносителя будет распределяться вдоль теплопровода по прямой и будет при этом знакопостоянной функцией, что, как правило, имеет место. В самом деле, в этом случае

1L1

t =     t ( L ) dL =— S_TP =

_{L 0}

1 t ⁰ + 1 ( L )       t ⁰ + 1 ( L )

=----L =,

L22

где S_ТР – площадь прямолинейной трапеции, образованной линейной знакопостоянной зависимостью t ( L ) и осью абсцисс на отрезке [0; L].

Погрешность вычисления средней температуры теплоносителя по формуле (4), очевидно, будет равна

• 8 = t ^- t yn = ⁽ t B ^- t ^{0) +}

n L      ( t ⁰ - t_B ) cGR_L t

• +[1 — exp(-      )lx[ -----В     L—"7].(6)

cGRl        nL2

Рассмотрим различные варианты определения погрешности вычисления средней температуры теплоносителя.

• 1.    Известно, что при малых значениях вели-nLn

чины L можно считать, что exp(--) ~1,

,           cGR_L     cGR_L ,

• т.    е. [1 - exp(—^^)] ® ^nR , поэтому погреш- cGR_L   cGR_L

• 2.    Если t_B <<  t ⁰, тогда погрешность вычисления средней температуры теплоносителя по упрощенной формуле будет равна

• 3.    Если одновременно L достаточно малая nL     п—0

ность вычисления средней температуры теплоносителя по упрощенной формуле будет равна - я L о = - tB------. Понятно, что в этом случае о ^ 0

2cGRL при L ^ 0. Кроме того, отсюда также видно, что погрешность оценки будет уменьшаться с увеличением любой из величин – удельной теплоемкости c , линейного термического сопротивления теплопередаче теплопровода RL и расхода теплоносителя G .

Инженерное оборудование зданий и сооружений nL    10 cGR o=-1 + [1 -exp(-     )]x —. Отсюда сле- cGRLn дует, что при прочих равных условиях, модуль погрешности растет с ростом температуры теплоносителя в начале участка t0 .

величина (т. е. [1 - exp(--)] ®------) и 1B << 1 , cGRL   cGRL то из последней формулы следует, что 0 - 0 .

Таким образом, погрешность вычисления средней температуры теплоносителя на участке по упрощенной формуле близка к нулю, только если длина участка трубопровода мала, а температура окружающей среды намного меньше температуры теплоносителя в трубопроводе. Во всех остальных случаях при определении средней температуры теплоносителя по формуле (4) появляется погрешность вычисления, которая в общем случае может быть найдена по формуле (6). Для примера найдем погрешность вычисления средней температуры теплоносителя по упрощенной формуле для случая, когда, например, использовалась обыкновенная водогазопроводная труба условным диаметром Dy = 20 мм и длиной 3 м. Линейное термическое сопротивление теплопередаче RL такого тепло- провода определили по экспериментальным данным методом работы [1], оно оказалось равным м - °С

• 2,49     . Пусть температура теплоносителя в

начале участка равна 10 = 90 °С , а температура окружающей среды 1В = 20 ° С . Расчет по формуле (6) дал следующие результаты: если расход теплоносителя равен G = 0,003 кг/с, то 5=-12,2 °С; если же G = 0,009 кг/с, то 5=-4,4 °С . Таким об- разом, погрешность вычисления средней температуры теплоносителя по упрощенной формуле уменьшается с увеличением расхода теплоносителя через трубопровод, что, как нетрудно видеть, вполне согласуется с вышеизложенным. Поскольку, как это хорошо видно из вышеприведенных соотношений, влияние теплоемкости теплоносителя c и линейного термического сопротивления теплопередаче теплопровода RL имеет тот же характер, то достаточно обоснованно можно утверждать, что с увеличением c и RL погрешность оценки также будет уменьшаться.

Известно, что из условия бесшумности скорость воды в трубопроводах систем отопления не должна превышать 0,8 м/с [3–5, 11], поэтому интересно узнать погрешность упрощенного вычисления средней температуры теплоносителя для расходов воды, соответствующих скоростям 0,5 ^ 0,8 м/с. Результаты таких расчетов для трубопровода с D_y = 20 мм и длиной 20 м приведены на рис. 2.

Как видно из рис. 2, для указанных условий модуль погрешности вычисления средней температуры теплоносителя по упрощенной формуле заметно увеличивается при малых расходах теплоносителя. Обуславливается это тем, что при малых расходах теплоносителя «похожесть» кривой распределения температуры теплоносителя вдоль трубы на прямую существенно уменьшается, ее кривизна [12] заметно увеличивается. Как было установлено выше, упрощенная формула дает точное значение средней температуры только при прямолинейном распределении температуры теплоносителя по длине теплопровода. Как известно [12], прямая представляет собой линию нулевой кривизны.

На рис. 3 показано, как меняется погрешность оценки в зависимости от длины участка для трех различных значений расхода теплоносителя, считая снизу вверх – для G = 0,05 кг/с; для G = 0,1 кг/с; для G = 0,2 кг/с.

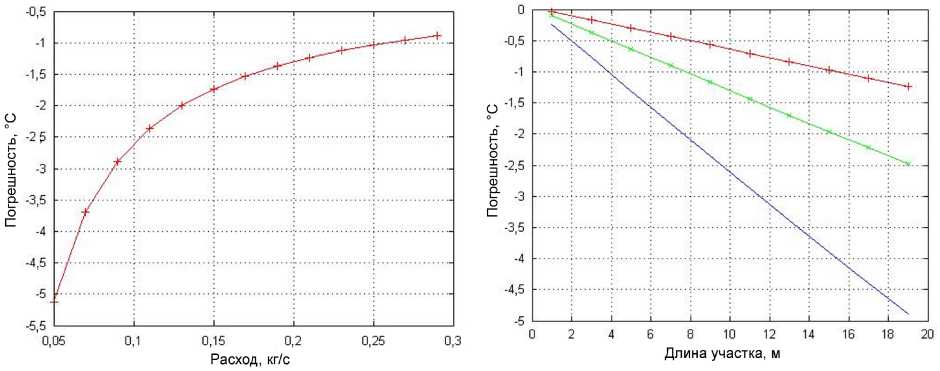
Рис. 2. Зависимость погрешности вычисления средней температуры теплоносителя на участке от его расхода

Рис. 3. Зависимость погрешности вычисления средней температуры теплоносителя от длины участка теплопровода

Как видно из рис. 3, с увеличением длины участка погрешность оценки средней температуры теплоносителя по упрощенной формуле по модулю растет, причем тем в большей степени, чем меньше расход.

Отметим также, что во всех наших расчетах получалось, что 5< 0 , т. е. Т < t y_n - упрощенная формула дает завышенное значение средней температуры, что может привести к просчетам при подборе оборудования и ограждающих конструкций [13–15].

Выводы

Рассмотрена задача оценки погрешности вычисления средней температуры теплоносителя на участке теплопровода по температурам двух его граничных точек. Найдена формула для погрешности оценки. Указаны факторы, влияющие на погрешность оценки, а также и случаи, когда упрощенная формула без существенной погрешности может быть применена для вычисления средней по длине участка температуры теплоносителя.